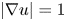1. Introduction
We consider an open set $\Omega \subset {\mathbb {R}}^2$![]() and $m\colon \Omega \to {\mathbb {R}}^2$
and $m\colon \Omega \to {\mathbb {R}}^2$![]() a solution of the eikonal equation
a solution of the eikonal equation
We are interested in particular in solutions that arise as limits as $\varepsilon \to 0$![]() of vector fields $m_\varepsilon$
of vector fields $m_\varepsilon$![]() with equi-bounded energy $\sup _{\varepsilon >0} F_\varepsilon (m_\varepsilon,\Omega ) < \infty$
with equi-bounded energy $\sup _{\varepsilon >0} F_\varepsilon (m_\varepsilon,\Omega ) < \infty$![]() , where
, where

are the functionals introduced by Aviles and Giga [Reference Aviles and Giga5]. We refer to the introduction of [Reference Jin and Kohn11] for a description of several physical applications.
The notion of entropy, borrowed from the field of conservation laws, plays a fundamental role in the study of the singular limit as $\varepsilon \to 0$![]() of these functionals. We say that a compactly supported function $\Phi \in C^\infty ({\mathbb {R}}^2,{\mathbb {R}}^2)$
of these functionals. We say that a compactly supported function $\Phi \in C^\infty ({\mathbb {R}}^2,{\mathbb {R}}^2)$![]() is an entropy for (1.1) if for every open set $U$
is an entropy for (1.1) if for every open set $U$![]() and every smooth $m:U\to {\mathbb {R}}^2$
and every smooth $m:U\to {\mathbb {R}}^2$![]() solving $\nabla \cdot m= 0$
solving $\nabla \cdot m= 0$![]() and $|m|=1$
and $|m|=1$![]() it holds $\nabla \cdot \Phi (m)=0$
it holds $\nabla \cdot \Phi (m)=0$![]() . It is shown in [Reference Ambrosio, De Lellis and Mantegazza3, Reference DeSimone, Müller, Kohn and Otto8] that functions with equi-bounded energy as $\varepsilon \to 0$
. It is shown in [Reference Ambrosio, De Lellis and Mantegazza3, Reference DeSimone, Müller, Kohn and Otto8] that functions with equi-bounded energy as $\varepsilon \to 0$![]() are pre-compact in $L^2(\Omega )$
are pre-compact in $L^2(\Omega )$![]() and any limit is an entropy solution of (1.1): namely, for every entropy $\Phi \in C^\infty ({\mathbb {R}}^2,{\mathbb {R}}^2)$
and any limit is an entropy solution of (1.1): namely, for every entropy $\Phi \in C^\infty ({\mathbb {R}}^2,{\mathbb {R}}^2)$![]() the distribution $\nabla \cdot \Phi (m)$
the distribution $\nabla \cdot \Phi (m)$![]() is a finite Radon measure. Remarkably, the same class of entropy solutions to (1.1) contains the asymptotic domain of other families of functionals: see [Reference Alouges, Rivière and Serfaty2, Reference Rivière and Serfaty17] for two micromagnetics models.
is a finite Radon measure. Remarkably, the same class of entropy solutions to (1.1) contains the asymptotic domain of other families of functionals: see [Reference Alouges, Rivière and Serfaty2, Reference Rivière and Serfaty17] for two micromagnetics models.
It is shown in [Reference Ghiraldin and Lamy9] that $m$![]() is an entropy solution if and only if the following kinetic equation (introduced in [Reference Jabin and Perthame10]) is satisfied:
is an entropy solution if and only if the following kinetic equation (introduced in [Reference Jabin and Perthame10]) is satisfied:
We denote by $\nu \in \mathcal {M}_{{\rm loc}}(\Omega )$![]() the entropy dissipation measure given by
the entropy dissipation measure given by
It is known [Reference De Lellis and Otto7] that $\mathcal {H}^1$![]() -a.e. point $x\in \Omega$
-a.e. point $x\in \Omega$![]() at which $\nu (B_r(x))/r\to 0$
at which $\nu (B_r(x))/r\to 0$![]() as $r\to 0^+$
as $r\to 0^+$![]() is a vanishing mean oscillation (VMO) point of $m$
is a vanishing mean oscillation (VMO) point of $m$![]() , that is,
, that is,

It is conjectured in [Reference De Lellis and Otto7, conjecture 1(b$'$![]() )] that $\mathcal {H}^1$
)] that $\mathcal {H}^1$![]() -a.e. such point is in fact a Lebesgue point. Our main result states that this conjecture is true under the additional assumption that $\nu (B_r(x))/r$
-a.e. such point is in fact a Lebesgue point. Our main result states that this conjecture is true under the additional assumption that $\nu (B_r(x))/r$![]() decays algebraically to 0.
decays algebraically to 0.
Theorem 1.1 Let $m\colon \Omega \to {\mathbb {R}}^2$![]() be an entropy solution (1.3) of the eikonal equation (1.1). Then $\mathcal {H}^1$
be an entropy solution (1.3) of the eikonal equation (1.1). Then $\mathcal {H}^1$![]() -a.e. $x\in \Omega$
-a.e. $x\in \Omega$![]() such that $\lim _{r\to 0^+}\nu (B_r(x))/r^{1+a}=0$
such that $\lim _{r\to 0^+}\nu (B_r(x))/r^{1+a}=0$![]() for some $a>0$
for some $a>0$![]() is a Lebesgue point of $m$
is a Lebesgue point of $m$![]() . In particular, the set of non-Lebesgue points of $m$
. In particular, the set of non-Lebesgue points of $m$![]() has Hausdorff dimension at most 1.
has Hausdorff dimension at most 1.
Remark 1.2 After this work was submitted, we became aware that the bound on the Hausdorff dimension can also be obtained as a consequence of classical capacity estimates [Reference Adams and Hedberg1, theorem 6.21] and of the regularity $m\in B^{1/3}_{3,\infty }$![]() [Reference Ghiraldin and Lamy9] (which implies $m\in W^{s,3}$
[Reference Ghiraldin and Lamy9] (which implies $m\in W^{s,3}$![]() for any $s<1/3$
for any $s<1/3$![]() ). Note however that the information provided by theorem 1.1 is stronger, in that it directly relates oscillations at a point $x$
). Note however that the information provided by theorem 1.1 is stronger, in that it directly relates oscillations at a point $x$![]() to the local energy dissipation $\nu (B_r(x))$
to the local energy dissipation $\nu (B_r(x))$![]() . Also note that, as will be clear from the proof, the assumption of algebraic energy decay $\nu (B_r)/r =\mathcal {O} (r^a)$
. Also note that, as will be clear from the proof, the assumption of algebraic energy decay $\nu (B_r)/r =\mathcal {O} (r^a)$![]() can be relaxed to $\nu (B_r)/r=\mathcal {O}(|\ln r|^{-14})$
can be relaxed to $\nu (B_r)/r=\mathcal {O}(|\ln r|^{-14})$![]() . Via a covering argument this implies that non-Lebesgue points are finite for the Hausdorff measure defined by the function $r\mapsto r|\ln r|^{-14}$
. Via a covering argument this implies that non-Lebesgue points are finite for the Hausdorff measure defined by the function $r\mapsto r|\ln r|^{-14}$![]() (see e.g. [Reference Adams and Hedberg1, § 5.1]), a fact which does not follow directly from capacity estimates.
(see e.g. [Reference Adams and Hedberg1, § 5.1]), a fact which does not follow directly from capacity estimates.
Analogues of theorem 1.1 have been obtained previously in [Reference Lamy and Otto13] for Burgers’ equation, and in [Reference Marconi16] for general scalar conservations laws. To prove theorem 1.1 we follow the scheme laid out in [Reference Marconi16], where it is shown that oscillations of averages ${\int\hskip -1,05em -\,} _{B_r(x)}u$![]() of the solution $u$
of the solution $u$![]() are controlled by the entropy dissipation. This, together with the VMO property, implies the Lebesgue point property. However, a key feature for the argument of [Reference Marconi16] is that the solution $u$
are controlled by the entropy dissipation. This, together with the VMO property, implies the Lebesgue point property. However, a key feature for the argument of [Reference Marconi16] is that the solution $u$![]() takes values in the ordered set ${\mathbb {R}}$
takes values in the ordered set ${\mathbb {R}}$![]() . Here, our solution $m$
. Here, our solution $m$![]() takes values in $\mathbb {S}^1$
takes values in $\mathbb {S}^1$![]() , and adapting the argument of [Reference Marconi16] is not enough to conclude (see proposition 1.4). Our proof of theorem 1.1 relies instead on the following dichotomy: either the oscillations of ${\int\hskip -1,05em -\,} _{B_r(x)}m$
, and adapting the argument of [Reference Marconi16] is not enough to conclude (see proposition 1.4). Our proof of theorem 1.1 relies instead on the following dichotomy: either the oscillations of ${\int\hskip -1,05em -\,} _{B_r(x)}m$![]() are controlled by the entropy dissipation $\nu$
are controlled by the entropy dissipation $\nu$![]() , or $m$
, or $m$![]() takes very different values in large subsets of $B_{R}(x)$
takes very different values in large subsets of $B_{R}(x)$![]() – this second alternative is ruled out by the VMO property. That dichotomy is made quantitative in the next statement.
– this second alternative is ruled out by the VMO property. That dichotomy is made quantitative in the next statement.
Proposition 1.3 Assume $B_1\subset \Omega$![]() . Let $r\in (0,1/2)$
. Let $r\in (0,1/2)$![]() and
and

There exist absolute constants $c,\delta >0$![]() such that, if
such that, if
then either
or there exist $s_0\in {\mathbb {R}}$![]() such that
such that
Here and in the rest of the article, we denote by $|A|$![]() the Lebesgue measure of a measurable set $A\subset {\mathbb {R}}^d$
the Lebesgue measure of a measurable set $A\subset {\mathbb {R}}^d$![]() . Theorem 1.1 is a rather direct consequence of proposition 1.3, as we explain now.
. Theorem 1.1 is a rather direct consequence of proposition 1.3, as we explain now.
Proof of theorem 1.1 Let $x\in \Omega$![]() be a VMO point of $m$
be a VMO point of $m$![]() such that $\nu (B_r(x))/r^{1+a}\to 0$
such that $\nu (B_r(x))/r^{1+a}\to 0$![]() for some $a>0$
for some $a>0$![]() . Translating and rescaling we assume without loss of generality that $x=0$
. Translating and rescaling we assume without loss of generality that $x=0$![]() and $B_1\subset \Omega$
and $B_1\subset \Omega$![]() . We claim that $h(r)= \mathcal {O}(r^b)$
. We claim that $h(r)= \mathcal {O}(r^b)$![]() for $b= a/(13+2a)>0$
for $b= a/(13+2a)>0$![]() . This, together with the fact that $0$
. This, together with the fact that $0$![]() is a VMO point of $m$
is a VMO point of $m$![]() , implies that $0$
, implies that $0$![]() is a Lebesgue point (see [Reference Marconi16, lemma 4.6]). (Note, in connection with remark 1.2, that $h(r)=\mathcal {O}(|\ln r|^{-1-\varepsilon })$
is a Lebesgue point (see [Reference Marconi16, lemma 4.6]). (Note, in connection with remark 1.2, that $h(r)=\mathcal {O}(|\ln r|^{-1-\varepsilon })$![]() for some $\varepsilon >0$
for some $\varepsilon >0$![]() would imply the same conclusion.) To prove that $h(r)=\mathcal {O}(r^b)$
would imply the same conclusion.) To prove that $h(r)=\mathcal {O}(r^b)$![]() we argue by contradiction and assume that $h(r)/r^b\to \infty$
we argue by contradiction and assume that $h(r)/r^b\to \infty$![]() along a sequence $r\to 0^+$
along a sequence $r\to 0^+$![]() . Then, along the same sequence,
. Then, along the same sequence,

Therefore, applying proposition 1.3 along the sequence $R\to 0$![]() , condition (1.6) cannot be satisfied because $\nu (B_R)/R^{1+a}\to 0$
, condition (1.6) cannot be satisfied because $\nu (B_R)/R^{1+a}\to 0$![]() , so we have (1.7). This contradicts the VMO property: for all small enough $R$
, so we have (1.7). This contradicts the VMO property: for all small enough $R$![]() , the projection $z_R\in \mathbb {S}^1$
, the projection $z_R\in \mathbb {S}^1$![]() of ${\int\hskip -1,05em -\,} _{B_R}m$
of ${\int\hskip -1,05em -\,} _{B_R}m$![]() onto $\mathbb {S}^1$
onto $\mathbb {S}^1$![]() satisfies
satisfies
But one can choose $s\in {\mathbb {R}}$![]() such that $\operatorname {dist}(s,\lbrace s_0,s_0+\pi \rbrace )\leq \pi /4$
such that $\operatorname {dist}(s,\lbrace s_0,s_0+\pi \rbrace )\leq \pi /4$![]() and
and
for any $z\in \mathbb {S}^1$![]() (if $z_R={\rm e}^{is_R}$
(if $z_R={\rm e}^{is_R}$![]() , any $s\in [s_R + 3\pi /4,s_R +5\pi /4]$
, any $s\in [s_R + 3\pi /4,s_R +5\pi /4]$![]() has that property). According to (1.7) this implies $|B_R \cap \lbrace |m-z_R|\geq \pi /12\rbrace | \geq cR^2$
has that property). According to (1.7) this implies $|B_R \cap \lbrace |m-z_R|\geq \pi /12\rbrace | \geq cR^2$![]() , in contradiction with (1.8). Hence, we have proved that $x$
, in contradiction with (1.8). Hence, we have proved that $x$![]() is a Lebesgue point. The estimate on the Hausdorff dimension of non-Lebesgue points follows via a covering argument (see e.g. [Reference Ambrosio, Fusco and Pallara4, theorem 2.56]).
is a Lebesgue point. The estimate on the Hausdorff dimension of non-Lebesgue points follows via a covering argument (see e.g. [Reference Ambrosio, Fusco and Pallara4, theorem 2.56]).
The proof of proposition 1.3 has two main ingredients. The first ingredient consists in adapting the arguments of [Reference Marconi16] to prove a dichotomy similar to proposition 1.3, but where the second option (1.7) is replaced by a statement which is not strong enough to conclude.
Proposition 1.4 Let $r\in (0,1/2)$![]() and $h$
and $h$![]() be as in proposition 1.3. There exist absolute constants $c,\delta >0$
be as in proposition 1.3. There exist absolute constants $c,\delta >0$![]() such that, if $R=32r/(\delta h^2)\leq 1$
such that, if $R=32r/(\delta h^2)\leq 1$![]() , then we have either $\nu (B_{R})\geq c h^{11} r$
, then we have either $\nu (B_{R})\geq c h^{11} r$![]() , or
, or
for some $m_0\in \mathbb {S}^1$![]() .
.
The main idea behind the argument in [Reference Marconi16] is that a large value of $h$![]() implies the existence of a configuration which would be impossible in the absence of entropy dissipation. In the presence of dissipation, such configuration provides a lower bound on the dissipation, and there is no dichotomy. Here instead, not all configurations created by large values of $h$
implies the existence of a configuration which would be impossible in the absence of entropy dissipation. In the presence of dissipation, such configuration provides a lower bound on the dissipation, and there is no dichotomy. Here instead, not all configurations created by large values of $h$![]() can be ruled out in the absence of dissipation: in particular the vortex solution $m(x)= x^\perp /|x|$
can be ruled out in the absence of dissipation: in particular the vortex solution $m(x)= x^\perp /|x|$![]() has zero dissipation but the values of $h(r)$
has zero dissipation but the values of $h(r)$![]() around the origin are not vanishing. This is reflected in the second alternative (1.9) of the dichotomy.
around the origin are not vanishing. This is reflected in the second alternative (1.9) of the dichotomy.
The second ingredient in our proof of proposition 1.3 consists in using the methods developed in [Reference Contreras Hip, Lamy and Marconi6, Reference Lamy and Marconi12, Reference Marconi14, Reference Marconi15] in order to pass from (1.9) to (1.7).
Proposition 1.5 Let $m_0={\rm e}^{is_0}\in \mathbb {S}^1$![]() , and $R>0$
, and $R>0$![]() such that $B_R\subset \Omega$
such that $B_R\subset \Omega$![]() . Then we have either
. Then we have either
or $\nu (B_R)\geq c R$![]() , or (1.7), for some absolute constant $c>0$
, or (1.7), for some absolute constant $c>0$![]() .
.
Proposition 1.3 follows readily from propositions 1.4 and 1.5. Thanks to proposition 1.4, we know indeed that either $\nu (B_R)\geq c h^{11}r$![]() , in which case we are done, or estimate (1.9) is valid. But according to proposition 1.5, if (1.9) is satisfied, then we have either $\nu (B_R)\geq c hr^2/R \geq c h^{11} r$
, in which case we are done, or estimate (1.9) is valid. But according to proposition 1.5, if (1.9) is satisfied, then we have either $\nu (B_R)\geq c hr^2/R \geq c h^{11} r$![]() , or $\nu (B_R)\geq c R\geq c h^{11}r$
, or $\nu (B_R)\geq c R\geq c h^{11}r$![]() , or (1.7). In all cases, proposition 1.3 is verified.
, or (1.7). In all cases, proposition 1.3 is verified.
The proofs of propositions 1.4 and 1.5 are presented in § 2 and § 3.
Notations.
We denote by $|A|$![]() the Lebesgue measure of a set $A\subset {\mathbb {R}}^d$
the Lebesgue measure of a set $A\subset {\mathbb {R}}^d$![]() . We use the symbol $\gtrsim$
. We use the symbol $\gtrsim$![]() to signify inequality up to an absolute multiplicative constant.
to signify inequality up to an absolute multiplicative constant.
2. Proof of proposition 1.4
Let $x_1,x_2$![]() attain the maximum in definition (1.5) of $h$
attain the maximum in definition (1.5) of $h$![]() , and define, for $j=1,2$
, and define, for $j=1,2$![]() , $\rho _j(s)$
, $\rho _j(s)$![]() as the proportion of points $x\in B_r(x_j)$
as the proportion of points $x\in B_r(x_j)$![]() at which $m(x)$
at which $m(x)$![]() lies in the semi-circle of direction ${\rm e}^{is}$
lies in the semi-circle of direction ${\rm e}^{is}$![]() , that is, for every $s\in {\mathbb {R}}/2\pi {\mathbb {Z}}$
, that is, for every $s\in {\mathbb {R}}/2\pi {\mathbb {Z}}$![]() , we set
, we set
where
Note that $|\rho _j|\leq 1$![]() and, since for every $x \in \Omega$
and, since for every $x \in \Omega$![]() it holds $|D_s\mathbf {1}_{E_m} (x,\cdot )| ( {\mathbb {R}}/2\pi {\mathbb {Z}}) =2$
it holds $|D_s\mathbf {1}_{E_m} (x,\cdot )| ( {\mathbb {R}}/2\pi {\mathbb {Z}}) =2$![]() , then $\rho _j\in BV({\mathbb {R}}/2\pi {\mathbb {Z}})$
, then $\rho _j\in BV({\mathbb {R}}/2\pi {\mathbb {Z}})$![]() with $|D\rho _j|({\mathbb {R}}/2\pi {\mathbb {Z}})\leq 2$
with $|D\rho _j|({\mathbb {R}}/2\pi {\mathbb {Z}})\leq 2$![]() . Moreover, by Fubini theorem, these functions satisfy the identities
. Moreover, by Fubini theorem, these functions satisfy the identities
For $s\in {\mathbb {R}}$![]() and $\rho >0$
and $\rho >0$![]() we denote by $I_\rho (s)$
we denote by $I_\rho (s)$![]() the segment
the segment
For a small enough absolute constant $\delta \in (0,1)$![]() , the subset $S\subset {\mathbb {R}}/2\pi {\mathbb {Z}}$
, the subset $S\subset {\mathbb {R}}/2\pi {\mathbb {Z}}$![]() given by
given by
satisfies $|S|\leq h /2$![]() (as follows e.g. from a Besicovitch covering argument). Thus, we have
(as follows e.g. from a Besicovitch covering argument). Thus, we have

We may therefore find $s\in {\mathbb {R}}/2\pi {\mathbb {Z}}$![]() such that $s\notin S$
such that $s\notin S$![]() and $|\rho _1(s)-\rho _2(s)|\geq h/{2\pi }$
and $|\rho _1(s)-\rho _2(s)|\geq h/{2\pi }$![]() . We assume without loss of generality that $\rho _1(s)-\rho _2(s)\geq h/2\pi$
. We assume without loss of generality that $\rho _1(s)-\rho _2(s)\geq h/2\pi$![]() , and by definition of $S$
, and by definition of $S$![]() we deduce
we deduce
In particular, setting $s_0=s-\pi /2 -3\delta h^2/4$![]() , we have
, we have

As $\rho _j(s+\pi )=1-\rho _j(s)$![]() for a.e. $s\in {\mathbb {R}}/2\pi {\mathbb {Z}}$
for a.e. $s\in {\mathbb {R}}/2\pi {\mathbb {Z}}$![]() , this implies
, this implies
The relevance of (2.2)–(2.3) comes from the following geometric observation. Given two directions $s_1\in I_{\delta h^2/4}(s_0+\pi /2)$![]() and $s_2\in I_{\delta h^2/4}(s_0-\pi /2+\delta h^2)$
and $s_2\in I_{\delta h^2/4}(s_0-\pi /2+\delta h^2)$![]() and two points $y_1\in B_r(x_1)\cap \lbrace m\cdot {\rm e}^{is_1}>0\rbrace$
and two points $y_1\in B_r(x_1)\cap \lbrace m\cdot {\rm e}^{is_1}>0\rbrace$![]() , $y_2\in B_r(x_2)\cap \lbrace m\cdot {\rm e}^{is_2}>0\rbrace$
, $y_2\in B_r(x_2)\cap \lbrace m\cdot {\rm e}^{is_2}>0\rbrace$![]() , we have $|s_1-s_2|\geq \delta h^2$
, we have $|s_1-s_2|\geq \delta h^2$![]() , and the two lines $y_j +{\mathbb {R}} {\rm e}^{is_j}$
, and the two lines $y_j +{\mathbb {R}} {\rm e}^{is_j}$![]() intersect at a point $z\in B_{8r/(\delta h^2)}$
intersect at a point $z\in B_{8r/(\delta h^2)}$![]() . In the absence of dissipation, one would have $m(z)\cdot {\rm e}^{is_j}>0$
. In the absence of dissipation, one would have $m(z)\cdot {\rm e}^{is_j}>0$![]() for $j=1,2$
for $j=1,2$![]() , and therefore $m(z)\cdot {\rm e}^{is_0}\geq \cos (2\delta h^2)\geq 1/2$
, and therefore $m(z)\cdot {\rm e}^{is_0}\geq \cos (2\delta h^2)\geq 1/2$![]() . The last lower bound is valid provided $\delta \leq \pi /24$
. The last lower bound is valid provided $\delta \leq \pi /24$![]() , since $|h|\leq 2$
, since $|h|\leq 2$![]() . The same argument with $s_1\in I_{\delta h^2/4}(s_0+\pi /2+\delta h^2)$
. The same argument with $s_1\in I_{\delta h^2/4}(s_0+\pi /2+\delta h^2)$![]() and $s_2\in I_{\delta h^2/4}(s_0-\pi /2)$
and $s_2\in I_{\delta h^2/4}(s_0-\pi /2)$![]() implies instead $m(z)\cdot {\rm e}^{is_0}\leq -1/2$
implies instead $m(z)\cdot {\rm e}^{is_0}\leq -1/2$![]() .
.
Thanks to the techniques in [Reference Marconi16], in the presence of dissipation this can be made quantitative. The main idea is that (1.3) provides an estimate on the difference between the ‘epigraph’ $E_m$![]() defined in (2.1) and its free transport ${\mathrm {FT}}(E_m,t)$
defined in (2.1) and its free transport ${\mathrm {FT}}(E_m,t)$![]() , where the free transport operator ${\mathrm {FT}}(\cdot,t)$
, where the free transport operator ${\mathrm {FT}}(\cdot,t)$![]() is defined for $t\in {\mathbb {R}}$
is defined for $t\in {\mathbb {R}}$![]() by
by
Lemma 2.1 Let $t\in {\mathbb {R}}$![]() and $\rho >0$
and $\rho >0$![]() such that $B_{\rho + |t|}\subset \Omega$
such that $B_{\rho + |t|}\subset \Omega$![]() . For all $\phi \in C_c^1(B_\rho \times {\mathbb {R}}/2\pi {\mathbb {Z}})$
. For all $\phi \in C_c^1(B_\rho \times {\mathbb {R}}/2\pi {\mathbb {Z}})$![]() we have
we have
Proof of lemma 2.1 Define $\chi,\chi ^{{\mathrm {FT}}}\colon [-|t|,|t|]\times \Omega \times {\mathbb {R}}/2\pi {\mathbb {Z}}\to {\mathbb {R}}$![]() by
by
so we have, in the sense of distributions,
Setting $\hat \chi =\chi ^{{\mathrm {FT}}}-\chi$![]() , and $\psi (\tau,x,s)=\phi (x+{\rm e}^{is}(t-\tau ),s)$
, and $\psi (\tau,x,s)=\phi (x+{\rm e}^{is}(t-\tau ),s)$![]() which satisfies $\partial _\tau \psi +{\rm e}^{is}\cdot \nabla _x\psi =0$
which satisfies $\partial _\tau \psi +{\rm e}^{is}\cdot \nabla _x\psi =0$![]() , we deduce
, we deduce
Integrating with respect to $(x,s)$![]() (this is formal but makes sense distributionally) we deduce
(this is formal but makes sense distributionally) we deduce
Integrating this from $0$![]() to $t$
to $t$![]() and recalling $\nu (A)=|\sigma |(A\times {\mathbb {R}}/2\pi {\mathbb {Z}})$
and recalling $\nu (A)=|\sigma |(A\times {\mathbb {R}}/2\pi {\mathbb {Z}})$![]() for $A\subset \Omega$
for $A\subset \Omega$![]() , we obtain
, we obtain

Noting that $\|\partial _s\psi \|_\infty \leq \|\partial _s\phi \|_\infty +|t| \,\|\nabla _x\phi \|_\infty$![]() completes the proof.
completes the proof.
Equipped with lemma 2.1 we continue the proof of proposition 1.4. First, we make use of (2.2). We define $\hat z\in {\mathbb {R}}^2$![]() as the intersection of the lines $x_1+{\mathbb {R}}\,{\rm e}^{i(s_0+\pi /2)}$
as the intersection of the lines $x_1+{\mathbb {R}}\,{\rm e}^{i(s_0+\pi /2)}$![]() and $x_2+{\mathbb {R}}\,{\rm e}^{i(s_0-\pi /2+\delta h^2)}$
and $x_2+{\mathbb {R}}\,{\rm e}^{i(s_0-\pi /2+\delta h^2)}$![]() , that is,
, that is,
for some $t_1,t_2\in {\mathbb {R}}$![]() . Since $|x_1-x_2|\leq 4r$
. Since $|x_1-x_2|\leq 4r$![]() , we have
, we have
and therefore $B_r(\hat z)\subset B_{R/2}$![]() . We will use lemma 2.1 to compare $E_m$
. We will use lemma 2.1 to compare $E_m$![]() with ${\mathrm {FT}}(E_m,t_1)$
with ${\mathrm {FT}}(E_m,t_1)$![]() and ${\mathrm {FT}}(E_m,t_2)$
and ${\mathrm {FT}}(E_m,t_2)$![]() on $B_r(\hat z)$
on $B_r(\hat z)$![]() . We define
. We define
with $c= \delta h^3/128\pi \le \delta h^2/4$![]() , and their free transport counterparts
, and their free transport counterparts
We estimate

Moreover,

where in the last inequality we used (2.4). Therefore, we have

and similarly

From (2.2) we know that
Integrating this inequality in $s\in [-c,c]$![]() , it follows from (2.5) and (2.6) that
, it follows from (2.5) and (2.6) that
by the choice $c=\delta h^3/128\pi$![]() . Next, we consider two cases, depending on whether $A_1$
. Next, we consider two cases, depending on whether $A_1$![]() and $A_2$
and $A_2$![]() satisfy a similar inequality.
satisfy a similar inequality.
Case 1. Assume first that
then
Moreover, since $\pi _x(A_1) \cup \pi _x(A_2) \subset B_r(\hat z)$![]() , it follows that $A:= \pi _x(A_1) \cap \pi _x(A_2)$
, it follows that $A:= \pi _x(A_1) \cap \pi _x(A_2)$![]() satisfies $|A|\ge h|B_r|/16$
satisfies $|A|\ge h|B_r|/16$![]() . By construction, we have
. By construction, we have

so this implies
Case 2. Assume now that
Then using (2.7) we obtain
so either $|A_1^{{\mathrm {FT}}}|-|A_1|$![]() or $|A_2^{{\mathrm {FT}}}|-|A_2|$
or $|A_2^{{\mathrm {FT}}}|-|A_2|$![]() is larger than half the right-hand side. We consider without loss of generality only the first case:
is larger than half the right-hand side. We consider without loss of generality only the first case:
This implies a lower bound on the entropy dissipation $\nu (B_{R})$![]() thanks to lemma 2.1. Specifically, we apply lemma 2.1 to $t=t_1$
thanks to lemma 2.1. Specifically, we apply lemma 2.1 to $t=t_1$![]() and $\phi \in C_c^\infty (B_{2r(\hat z)}\times I_{2c}(s_0+\pi /2))$
and $\phi \in C_c^\infty (B_{2r(\hat z)}\times I_{2c}(s_0+\pi /2))$![]() such that
such that
and $|\partial _s\phi |\leq 2/(\varepsilon c)$![]() , $|\nabla _x\phi |\leq 2/(\varepsilon r)$
, $|\nabla _x\phi |\leq 2/(\varepsilon r)$![]() . We choose $\varepsilon =h/192\pi$
. We choose $\varepsilon =h/192\pi$![]() to ensure
to ensure
Since $|t_1|\leq 8r/(\delta h^2)$![]() and $B_{2r+|t_1|}(\hat z)\subset B_R$
and $B_{2r+|t_1|}(\hat z)\subset B_R$![]() , we deduce $\nu (B_R)\gtrsim \delta ^3 h^{11} r \gtrsim h^{11}r$
, we deduce $\nu (B_R)\gtrsim \delta ^3 h^{11} r \gtrsim h^{11}r$![]() .
.
Similarly, using (2.3) we have two cases: either
or $\nu (B_R)\gtrsim h^{11} r$![]() . So gathering all cases, we see that either both (2.8) and (2.9) are satisfied, or $\nu (B_R)\gtrsim h^{11}r$
. So gathering all cases, we see that either both (2.8) and (2.9) are satisfied, or $\nu (B_R)\gtrsim h^{11}r$![]() , which is exactly the dichotomy of proposition 1.4.
, which is exactly the dichotomy of proposition 1.4.
3. Proof of proposition 1.5
To prove proposition 1.5, we briefly recall from [Reference Marconi14] the notion of Lagrangian representation of an entropy solution $m$![]() of the eikonal equation. In [Reference Marconi14, Reference Marconi15], the second author shows the existence of a finite non-negative Radon measure $\omega$
of the eikonal equation. In [Reference Marconi14, Reference Marconi15], the second author shows the existence of a finite non-negative Radon measure $\omega$![]() on the set of curves:
on the set of curves:

with the following three properties:
• for every $t\in (0,1)$
 , the pushforward of $\omega$
, the pushforward of $\omega$ , restricted to the section $\Gamma (t)=\lbrace (\gamma,t^-_\gamma,t^+_\gamma )\in \Gamma \colon t_\gamma ^- < t < t_\gamma ^+\rbrace$
, restricted to the section $\Gamma (t)=\lbrace (\gamma,t^-_\gamma,t^+_\gamma )\in \Gamma \colon t_\gamma ^- < t < t_\gamma ^+\rbrace$ , by the evaluation map $e_t\colon \gamma \mapsto \gamma (t)$
, by the evaluation map $e_t\colon \gamma \mapsto \gamma (t)$ (a right-continuous representative of $\gamma _s$
(a right-continuous representative of $\gamma _s$ is always considered), is uniform on the ‘epigraph’ $E_m=\lbrace m(x)\cdot {\rm e}^{is}>0\rbrace$
is always considered), is uniform on the ‘epigraph’ $E_m=\lbrace m(x)\cdot {\rm e}^{is}>0\rbrace$ , that is,
(3.1)\begin{equation} ( e_t)_\sharp \left[ \omega \lfloor \Gamma(t)\right]= \mathbf 1_{m(x)\cdot {\rm e}^{is}>0}\,{\rm d}x\,{\rm d}s ; \end{equation}
, that is,
(3.1)\begin{equation} ( e_t)_\sharp \left[ \omega \lfloor \Gamma(t)\right]= \mathbf 1_{m(x)\cdot {\rm e}^{is}>0}\,{\rm d}x\,{\rm d}s ; \end{equation}
• the measure $\omega$
 is concentrated on curves $(\gamma,t^-_\gamma,t^+_\gamma )\in \Gamma$
is concentrated on curves $(\gamma,t^-_\gamma,t^+_\gamma )\in \Gamma$ solving the characteristic equation:
(3.2)\begin{equation} \dot\gamma_x(t)= {\rm e}^{i \gamma_s(t)}\quad\text{for a.e. }t\in (t^-_\gamma,t^+_\gamma); \end{equation}
solving the characteristic equation:
(3.2)\begin{equation} \dot\gamma_x(t)= {\rm e}^{i \gamma_s(t)}\quad\text{for a.e. }t\in (t^-_\gamma,t^+_\gamma); \end{equation}
• the entropy dissipation measure (1.4) disintegrates along the Lagrangian curves as
(3.3)\begin{equation} \nu(A)= \int_\Gamma \mu_\gamma (\gamma_x^{{-}1}(A))\,{\rm d}\omega(\gamma)\quad\text{for all measurable }A\subset\Omega, \end{equation}where $\mu _\gamma =|D_t\gamma _s|$
 , with the convention that a jump of $\gamma _s$
, with the convention that a jump of $\gamma _s$ from $s^-$
from $s^-$ to $s^+$
to $s^+$ at time $t_0\in (t_\gamma ^-,t_\gamma ^+)$
at time $t_0\in (t_\gamma ^-,t_\gamma ^+)$ contributes $\operatorname {dist}_{{\mathbb {R}}/2\pi {\mathbb {Z}}}(s^-,s^+)\delta _{t=t_0}$
contributes $\operatorname {dist}_{{\mathbb {R}}/2\pi {\mathbb {Z}}}(s^-,s^+)\delta _{t=t_0}$ to the jump part of $\mu _\gamma$
to the jump part of $\mu _\gamma$ (see [Reference Marconi14, proposition 2.5]).
(see [Reference Marconi14, proposition 2.5]).
Moreover, the Lagrangian property (3.1) implies that $\omega$![]() is concentrated on curves $\gamma$
is concentrated on curves $\gamma$![]() such that $\gamma _x(t)$
such that $\gamma _x(t)$![]() is a Lebesgue point of $m$
is a Lebesgue point of $m$![]() with $m(\gamma _x(t))\cdot {\rm e}^{i\gamma _s(t^+)}>0$
with $m(\gamma _x(t))\cdot {\rm e}^{i\gamma _s(t^+)}>0$![]() , for a.e. $t\in (0,1)$
, for a.e. $t\in (0,1)$![]() [Reference Marconi14, lemma 2.7]. We denote by $\Gamma _g\subset \Gamma$
[Reference Marconi14, lemma 2.7]. We denote by $\Gamma _g\subset \Gamma$![]() the full-measure subset of Lagrangian curves which satisfy that property together with the characteristic equation (3.2).
the full-measure subset of Lagrangian curves which satisfy that property together with the characteristic equation (3.2).
The proof of proposition 1.5 is based on two main tools. The first, lemma 3.1, is a dichotomy stating that either Lagrangian curves passing through a given set create a lot of dissipation, or one can find an almost-straight Lagrangian curve passing through that set. The second ([Reference Lamy and Marconi12, lemma 5.2], a slightly more precise version of [Reference Marconi14, lemma 3.1], itself adapted from [Reference Marconi15, lemma 22]) is another dichotomy: given an almost-straight Lagrangian curve, either the density of points at which $m$![]() lies in the semi-circle indicated by the $s$
lies in the semi-circle indicated by the $s$![]() -component of that curve is high, or a lot of dissipation must be created. The succession of these two dichotomies is reflected in the three alternatives in the conclusion of proposition 1.5. We first state and prove the first tool, and then proceed to the proof of proposition 1.5.
-component of that curve is high, or a lot of dissipation must be created. The succession of these two dichotomies is reflected in the three alternatives in the conclusion of proposition 1.5. We first state and prove the first tool, and then proceed to the proof of proposition 1.5.
Lemma 3.1 For any $R>0$![]() such that $B_R\subset \Omega$
such that $B_R\subset \Omega$![]() , any measurable set $A\subset B_{R}\times {\mathbb {R}}/2\pi {\mathbb {Z}}$
, any measurable set $A\subset B_{R}\times {\mathbb {R}}/2\pi {\mathbb {Z}}$![]() , and any $\eta \in (0,1)$
, and any $\eta \in (0,1)$![]() , we have either
, we have either
or there exists a curve $\gamma \in \Gamma _g$![]() and a connected component $J$
and a connected component $J$![]() of $\gamma _x^{-1}(B_R)$
of $\gamma _x^{-1}(B_R)$![]() such that
such that
Proof of lemma 3.1 Assume that the second alternative of lemma 3.1 is not verified: for every curve $\gamma \in \Gamma _g$![]() and every connected component $J$
and every connected component $J$![]() of $\gamma _x^{-1}(B_R)$
of $\gamma _x^{-1}(B_R)$![]() intersecting $\gamma ^{-1}(A)$
intersecting $\gamma ^{-1}(A)$![]() , we have $\mu _\gamma (J) >\eta$
, we have $\mu _\gamma (J) >\eta$![]() . Then we claim that
. Then we claim that
for all $\gamma \in \Gamma _g$![]() . To prove (3.5), denote by $J_k=(t_k^-,t_k^+)$
. To prove (3.5), denote by $J_k=(t_k^-,t_k^+)$![]() the connected components of $\gamma _x^{-1}(B_R)$
the connected components of $\gamma _x^{-1}(B_R)$![]() which intersect $\gamma ^{-1}(A)$
which intersect $\gamma ^{-1}(A)$![]() . We show next that $\mu _\gamma (J_k)\gtrsim \eta |J_k|/ R$
. We show next that $\mu _\gamma (J_k)\gtrsim \eta |J_k|/ R$![]() for all $k$
for all $k$![]() . On the one hand, if $|J_k|\leq 4R$
. On the one hand, if $|J_k|\leq 4R$![]() then $\mu _\gamma (J_k)\gtrsim \eta |J_k|/ R$
then $\mu _\gamma (J_k)\gtrsim \eta |J_k|/ R$![]() because $\mu _\gamma (J_k)> \eta$
because $\mu _\gamma (J_k)> \eta$![]() by assumption. On the other, from the characteristic equation (3.2) and the definition of $\mu _\gamma =|D_t\gamma _s|$
by assumption. On the other, from the characteristic equation (3.2) and the definition of $\mu _\gamma =|D_t\gamma _s|$![]() , we have the inequality:
, we have the inequality:
and we deduce that in any interval $J\subset (0,1)$![]() such that $\gamma _x(J)\subset B_R$
such that $\gamma _x(J)\subset B_R$![]() and $|J|\geq 4R$
and $|J|\geq 4R$![]() , we must have $\mu _\gamma (J) \geq 1/2$
, we must have $\mu _\gamma (J) \geq 1/2$![]() . Therefore, if $|J_k|\geq 4R$
. Therefore, if $|J_k|\geq 4R$![]() , cutting $J_k$
, cutting $J_k$![]() in disjoint subintervals of length between $4R$
in disjoint subintervals of length between $4R$![]() and $8R$
and $8R$![]() , we obtain that $\mu _\gamma (J_k) \gtrsim |J_k|/R \geq \eta |J_k|/ R$
, we obtain that $\mu _\gamma (J_k) \gtrsim |J_k|/R \geq \eta |J_k|/ R$![]() . So we have
. So we have
which implies (3.5) since $\gamma ^{-1}(A)\subset \bigcup _k J_k$![]() . From (3.5) and the fact that $\omega (\Gamma {\setminus} \Gamma _g)=0$
. From (3.5) and the fact that $\omega (\Gamma {\setminus} \Gamma _g)=0$![]() we infer
we infer
where the first equality comes from disintegration (3.3). Making use of the Lagrangian property (3.1) to rewrite the last expression, we see that it is precisely equal to the right-hand side of (3.4), which concludes the proof of lemma 3.1.
Proof of proposition 1.5 We recall that $m_0={\rm e}^{is_0}$![]() and the sets $X_\pm$
and the sets $X_\pm$![]() are defined by
are defined by
For any $\hat s\in [s_0-\pi /4,s_0+\pi /4]$![]() , we apply lemma 3.1 to $A(\hat s)=B_{R/2}\times I_\eta (\hat s)$
, we apply lemma 3.1 to $A(\hat s)=B_{R/2}\times I_\eta (\hat s)$![]() , where $I_\eta (\hat s)=[\hat s-\eta,\hat s+\eta ]$
, where $I_\eta (\hat s)=[\hat s-\eta,\hat s+\eta ]$![]() . If $\eta \in (0,\pi /12)$
. If $\eta \in (0,\pi /12)$![]() then we have $m(x)\cdot {\rm e}^{is}>0$
then we have $m(x)\cdot {\rm e}^{is}>0$![]() for all $(x,s)\in X_+\times I_\eta (\hat s)$
for all $(x,s)\in X_+\times I_\eta (\hat s)$![]() , and therefore,
, and therefore,
So, we have either $\nu (B_R)\gtrsim \eta ^2|X_+|/R$![]() , or there exists a curve $\gamma \in \Gamma _g$
, or there exists a curve $\gamma \in \Gamma _g$![]() and a connected component $J$
and a connected component $J$![]() of $\gamma _x^{-1}(B_R)$
of $\gamma _x^{-1}(B_R)$![]() intersecting $A(\hat s)$
intersecting $A(\hat s)$![]() such that $\mu _\gamma (J)<\eta$
such that $\mu _\gamma (J)<\eta$![]() . In that second case, applying [Reference Lamy and Marconi12, lemma 5.2] we deduce that either $\nu (B_R)\gtrsim \eta ^3 R$
. In that second case, applying [Reference Lamy and Marconi12, lemma 5.2] we deduce that either $\nu (B_R)\gtrsim \eta ^3 R$![]() or $|B_R\cap \lbrace m\cdot {\rm e}^{i\hat s}\geq -2\eta \rbrace |\gtrsim \eta R^2$
or $|B_R\cap \lbrace m\cdot {\rm e}^{i\hat s}\geq -2\eta \rbrace |\gtrsim \eta R^2$![]() . We fix $\eta =1/4$
. We fix $\eta =1/4$![]() and summarize the preceding discussion: for all $\hat s\in [s_0-\pi /4,s_0+\pi /4]$
and summarize the preceding discussion: for all $\hat s\in [s_0-\pi /4,s_0+\pi /4]$![]() , we have
, we have
Similarly, for all $\hat s\in [s_0+3\pi /4,s_0+5\pi /4]$![]() , we have
, we have
We conclude that we have either (1.10), or $\nu (B_R)\gtrsim R$![]() , or
, or
for all $s\in [s_0-\pi /4,s_0+\pi /4]\cup [s_0+3\pi /4,s_0+5\pi /4]$![]() . This corresponds exactly to the three alternatives in the statement of proposition 1.5.
. This corresponds exactly to the three alternatives in the statement of proposition 1.5.
Acknowledgements
We would like to thank Bogdan Raiţă for pointing out to us the capacity argument in remark 1.2. Part of this work was completed during X.L.'s stay at the EPFL's Institute of Mathematics, which he thanks for their hospitality. X.L. received support from ANR project ANR-22-CE40-0006. E.M. acknowledges the support received from the SNF Grant 182565 and the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant No. 101025032.