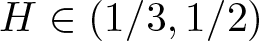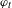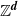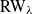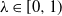Refine search
Actions for selected content:
13 results
Large deviation principle for slow-fast rough differential equations via controlled rough paths
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 January 2025, pp. 1-31
-
- Article
- Export citation
Invariant measures and large deviation principles for stochastic Schrödinger delay lattice systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1813-1854
- Print publication:
- October 2025
-
- Article
- Export citation
Unique equilibrium states, large deviations and Lyapunov spectra for the Katok map
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 20 March 2020, pp. 2182-2219
- Print publication:
- July 2021
-
- Article
- Export citation
An invariance principle and a large deviation principle for the biased random walk on
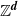 ${\mathbb{Z}}^{\lowercase{\textbf{\textit{d}}}}$
${\mathbb{Z}}^{\lowercase{\textbf{\textit{d}}}}$
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 295-313
- Print publication:
- March 2020
-
- Article
- Export citation
Large deviation principle for epidemic models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 15 September 2017, pp. 905-920
- Print publication:
- September 2017
-
- Article
- Export citation
Large deviation principles for connectable receivers in wireless networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 11 January 2017, pp. 1061-1094
- Print publication:
- December 2016
-
- Article
- Export citation
Laplace transform asymptotics and large deviation principles for longest success runs in Bernoulli trials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 747-764
- Print publication:
- September 2016
-
- Article
- Export citation
Limit theorems for a supercritical Poisson random indexed branching process
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 307-314
- Print publication:
- March 2016
-
- Article
- Export citation
A Minimum Action Method with Optimal Linear Time Scaling
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 5 / November 2015
- Published online by Cambridge University Press:
- 23 November 2015, pp. 1352-1379
- Print publication:
- November 2015
-
- Article
- Export citation
A generalized mean-reverting equation andapplications
-
- Journal:
- ESAIM: Probability and Statistics / Volume 18 / 2014
- Published online by Cambridge University Press:
- 22 October 2014, pp. 799-828
- Print publication:
- 2014
-
- Article
- Export citation
Asymptotic equipartition properties for simple hierarchical and networked structures
-
- Journal:
- ESAIM: Probability and Statistics / Volume 16 / 2012
- Published online by Cambridge University Press:
- 03 July 2012, pp. 114-138
- Print publication:
- 2012
-
- Article
- Export citation
A Markov Chain Analysis of Genetic Algorithms: Large Deviation Principle Approach
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 4 / December 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 967-975
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
A large deviation principle for a Brownian immigration particle system
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1120-1133
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation