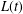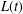Refine search
Actions for selected content:
5 results
Large and moderate deviations in Poisson navigations
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 10 September 2025, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moderate deviations of many-server queues via idempotent processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 708-742
- Print publication:
- June 2025
-
- Article
- Export citation
A large-deviation principle for birth–death processes with a linear rate of downward jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 31 October 2023, pp. 781-801
- Print publication:
- September 2024
-
- Article
- Export citation
LARGE DEVIATIONS FOR THE LONGEST GAP IN POISSON PROCESSES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 16 October 2019, pp. 146-156
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Large deviations for super-Brownian motion with immigration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 1 / March 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 187-201
- Print publication:
- March 2004
-
- Article
- Export citation