We study bracket words, which are a far-reaching generalization of Sturmian words, along Hardy field sequences, which are a far-reaching generalization of Piatetski-Shapiro sequences 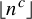 $\lfloor n^c \rfloor $. We show that sequences thus obtained are deterministic (that is, they have subexponential subword complexity) and satisfy Sarnak’s conjecture.
$\lfloor n^c \rfloor $. We show that sequences thus obtained are deterministic (that is, they have subexponential subword complexity) and satisfy Sarnak’s conjecture.