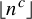1 Introduction
One of the key results in a recent paper [Reference Deshouillers, Drmota, Müllner, Shubin and SpiegelhoferDDM+22] by Deshouillers et al states that for each
![]() $m \in \mathbb {N}$
and
$m \in \mathbb {N}$
and
![]() $c> 1$
, the subword complexity of the sequence
$c> 1$
, the subword complexity of the sequence
![]() $(\lfloor n^c \rfloor \bmod m)_{n=0}^{\infty }$
grows at most polynomially, which in particular shows that this sequence is deterministic. The philosophy behind this result is the following: if we take a regularly growing function (
$(\lfloor n^c \rfloor \bmod m)_{n=0}^{\infty }$
grows at most polynomially, which in particular shows that this sequence is deterministic. The philosophy behind this result is the following: if we take a regularly growing function (
![]() $(\lfloor n^c \rfloor )_{n=0}^{\infty }$
) and apply a very simple rule to it (taking the residue modulo m), then the resulting sequence is still quite simple (in this case it has polynomial subword complexity). In this paper we vastly generalize both main aspects of this result, that is, we replace
$(\lfloor n^c \rfloor )_{n=0}^{\infty }$
) and apply a very simple rule to it (taking the residue modulo m), then the resulting sequence is still quite simple (in this case it has polynomial subword complexity). In this paper we vastly generalize both main aspects of this result, that is, we replace
![]() $(\lfloor n^c \rfloor )_{n=0}^{\infty }$
with Hardy sequences and we replace taking the residue modulo m by applying a bracket word.
$(\lfloor n^c \rfloor )_{n=0}^{\infty }$
with Hardy sequences and we replace taking the residue modulo m by applying a bracket word.
Sturmian words are among the simplest and most extensively studied classes of infinite words over a finite alphabet. One of their defining properties is extremely low subword complexity. Recall that the subword complexity of an infinite word
![]() $\mathbf a = (a(n))_{n=0}^\infty $
over a finite alphabet
$\mathbf a = (a(n))_{n=0}^\infty $
over a finite alphabet
![]() $\Sigma $
is the function
$\Sigma $
is the function
![]() $p_{\mathbf a}$
which assigns to each integer N the number
$p_{\mathbf a}$
which assigns to each integer N the number
![]() $p_{\mathbf a}(N)$
of words
$p_{\mathbf a}(N)$
of words
![]() $w \in \Sigma ^N$
which appear in
$w \in \Sigma ^N$
which appear in
![]() ${\mathbf a}$
. If there exists at least one value of N such that
${\mathbf a}$
. If there exists at least one value of N such that
![]() $p_{\mathbf a}(N) \leq N$
then a must be eventually periodic, in which case
$p_{\mathbf a}(N) \leq N$
then a must be eventually periodic, in which case
![]() $p_{\mathbf a}$
is bounded. If
$p_{\mathbf a}$
is bounded. If
![]() ${\mathbf a}$
is a Sturmian word then
${\mathbf a}$
is a Sturmian word then
![]() $p_{\mathbf a}(N) = N+1$
for all N, which in light of the remark above is the least subword complexity possible for a word that is not eventually periodic. In [Reference Adamczewski and KoniecznyAK23] Adamczewski and the first-named author studied a generalization of Sturmian words obtained by considering letter-to-letter codings of finite-valued generalized polynomials, which they dubbed bracket words. A generalized polynomial is an expression built from the usual polynomials using addition, multiplication and the integer part function. More precisely, generalized polynomials from
$p_{\mathbf a}(N) = N+1$
for all N, which in light of the remark above is the least subword complexity possible for a word that is not eventually periodic. In [Reference Adamczewski and KoniecznyAK23] Adamczewski and the first-named author studied a generalization of Sturmian words obtained by considering letter-to-letter codings of finite-valued generalized polynomials, which they dubbed bracket words. A generalized polynomial is an expression built from the usual polynomials using addition, multiplication and the integer part function. More precisely, generalized polynomials from
![]() $\mathbb {Z}$
to
$\mathbb {Z}$
to
![]() $\mathbb {R}$
are the smallest class of sequences that contain the usual polynomials, and such that if
$\mathbb {R}$
are the smallest class of sequences that contain the usual polynomials, and such that if
![]() $g,h \colon \mathbb {Z} \to \mathbb {R}$
are generalized polynomials then so are
$g,h \colon \mathbb {Z} \to \mathbb {R}$
are generalized polynomials then so are
![]() $g+h,\ g \cdot h$
and
$g+h,\ g \cdot h$
and
![]() $\lfloor g \rfloor $
. A bracket word is an infinite word
$\lfloor g \rfloor $
. A bracket word is an infinite word
![]() $\mathbf a = (a(n))_{n=0}^\infty $
over some finite alphabet
$\mathbf a = (a(n))_{n=0}^\infty $
over some finite alphabet
![]() $\Sigma $
which takes the form
$\Sigma $
which takes the form
![]() $a(n) = \varphi (g(n))$
for some generalized polynomial g such that
$a(n) = \varphi (g(n))$
for some generalized polynomial g such that
![]() $g(\mathbb {Z})$
is finite and some map
$g(\mathbb {Z})$
is finite and some map
![]() $\varphi \colon \mathbb {Z} \to \Sigma $
. For instance, Sturmian words (up to letter-to-letter coding) take the form
$\varphi \colon \mathbb {Z} \to \Sigma $
. For instance, Sturmian words (up to letter-to-letter coding) take the form
with
![]() $\alpha \in (0,1) \setminus \mathbb {Q}$
and
$\alpha \in (0,1) \setminus \mathbb {Q}$
and
![]() $\beta \in (0,1)$
(possibly with the integer part
$\beta \in (0,1)$
(possibly with the integer part
![]() $\lfloor \cdot \rfloor $
replaced by the ceiling
$\lfloor \cdot \rfloor $
replaced by the ceiling
![]() $\lceil {\cdot }\rceil $
), and hence are special cases of bracket words. One of the main results of [Reference Adamczewski and KoniecznyAK23] is a polynomial bound on subword complexity of bracket words:
$\lceil {\cdot }\rceil $
), and hence are special cases of bracket words. One of the main results of [Reference Adamczewski and KoniecznyAK23] is a polynomial bound on subword complexity of bracket words:
![]() $p_{\mathbf a}(N) \ll N^C$
for a constant C (dependent on
$p_{\mathbf a}(N) \ll N^C$
for a constant C (dependent on
![]() $\mathbf a$
).
$\mathbf a$
).
In [Reference Deshouillers, Drmota, Müllner, Shubin and SpiegelhoferDDM+22], Deshouillers et al investigated synchronizing automatic sequences along Piatetski-Shapiro sequences
![]() $(\lfloor n^c \rfloor )_{n=0}^\infty $
, where
$(\lfloor n^c \rfloor )_{n=0}^\infty $
, where
![]() $c> 1$
. A special case which plays a crucial role in the argument is when the synchronizing automatic sequence is periodic, in which case they obtained a polynomial bound on the subword complexity.
$c> 1$
. A special case which plays a crucial role in the argument is when the synchronizing automatic sequence is periodic, in which case they obtained a polynomial bound on the subword complexity.
As a joint extension of the two lines of investigation discussed above, we investigate bracket words along Piatetski-Shapiro sequences. In fact, we can deal with a considerably larger class of Hardy field functions with polynomial growth, which in addition to
![]() $n^c$
(
$n^c$
(
![]() $c> 1$
) include logarithmic-exponential expressions such as
$c> 1$
) include logarithmic-exponential expressions such as
![]() $\alpha n^{c} + \alpha ' n^{c'}$
and
$\alpha n^{c} + \alpha ' n^{c'}$
and
![]() $n^c \log ^{c'} n$
, as well as some more complicated expressions such as
$n^c \log ^{c'} n$
, as well as some more complicated expressions such as
![]() $\log (n!)$
. Our first result is a bound on the subword complexity.
$\log (n!)$
. Our first result is a bound on the subword complexity.
Theorem A. Let
![]() ${\mathbf a} = (a(n))_{n \in \mathbb {Z}}$
be a (two-sided) bracket word over the alphabet
${\mathbf a} = (a(n))_{n \in \mathbb {Z}}$
be a (two-sided) bracket word over the alphabet
![]() $\Sigma $
and let
$\Sigma $
and let
![]() $f \colon \mathbb {R}_+ \to \mathbb {R}$
be a Hardy field function with polynomial growth. Then the subword complexity of
$f \colon \mathbb {R}_+ \to \mathbb {R}$
be a Hardy field function with polynomial growth. Then the subword complexity of
![]() $(a(\lfloor f(n) \rfloor )_{n = 0}^\infty $
is bounded by
$(a(\lfloor f(n) \rfloor )_{n = 0}^\infty $
is bounded by
![]() $\exp (O(N^{\delta }))$
for some
$\exp (O(N^{\delta }))$
for some
![]() $0<\delta <1$
.
$0<\delta <1$
.
The study of (special) automatic sequences along Piatetski-Shapiro sequences
![]() $\lfloor n^c \rfloor $
has a long history. We mention results by Mauduit and Rivat [Reference Mauduit and RivatMR95, Reference Mauduit and RivatMR05], Deshouillers, Drmota and Morgenbesser [Reference Deshouillers, Drmota and MorgenbesserDDM12], Spiegelhofer [Reference SpiegelhoferSpi15, Reference SpiegelhoferSpi20], and Spiegelhofer and the second-named author [Reference Müllner and SpiegelhoferMS17]. Interestingly, two very different situations can appear. On the one hand, the Thue–Morse sequence along Piatetski-Shapiro sequences (for
$\lfloor n^c \rfloor $
has a long history. We mention results by Mauduit and Rivat [Reference Mauduit and RivatMR95, Reference Mauduit and RivatMR05], Deshouillers, Drmota and Morgenbesser [Reference Deshouillers, Drmota and MorgenbesserDDM12], Spiegelhofer [Reference SpiegelhoferSpi15, Reference SpiegelhoferSpi20], and Spiegelhofer and the second-named author [Reference Müllner and SpiegelhoferMS17]. Interestingly, two very different situations can appear. On the one hand, the Thue–Morse sequence along Piatetski-Shapiro sequences (for
![]() $1<c<3/2$
) is normal; in particular it has maximal subword complexity. On the other hand, synchronizing automatic sequences along Piatetski-Shapiro sequences are very far from normal; they have subexponential subword complexity. One natural generalization of automatic sequences are morphic sequences. These are letter-to-letter codings of fixed points of substitutions. A prominent morphic sequence is the Fibonacci word which is the fixed point of the substitution
$1<c<3/2$
) is normal; in particular it has maximal subword complexity. On the other hand, synchronizing automatic sequences along Piatetski-Shapiro sequences are very far from normal; they have subexponential subword complexity. One natural generalization of automatic sequences are morphic sequences. These are letter-to-letter codings of fixed points of substitutions. A prominent morphic sequence is the Fibonacci word which is the fixed point of the substitution
![]() $0 \mapsto 01, 1 \mapsto 0$
. Moreover, this sequence is also a Sturmian word and many interesting morphic sequences are also Sturmian words (see, for example, [Reference Klouda, Medková, Pelantová and StarostaKMPS18]). Thus, we obtain as a very special case (one of) the first results for morphic sequences along Piatetski-Shapiro sequences.
$0 \mapsto 01, 1 \mapsto 0$
. Moreover, this sequence is also a Sturmian word and many interesting morphic sequences are also Sturmian words (see, for example, [Reference Klouda, Medková, Pelantová and StarostaKMPS18]). Thus, we obtain as a very special case (one of) the first results for morphic sequences along Piatetski-Shapiro sequences.
It follows from Theorem A that the sequence
![]() $(a(\lfloor f(n) \rfloor )_{n = 0}^\infty $
is deterministic, meaning that it has subexponential subword complexity. A conjecture of Sarnak [Reference SarnakSar11] asserts that each deterministic sequence should be orthogonal to the Möbius function, given by
$(a(\lfloor f(n) \rfloor )_{n = 0}^\infty $
is deterministic, meaning that it has subexponential subword complexity. A conjecture of Sarnak [Reference SarnakSar11] asserts that each deterministic sequence should be orthogonal to the Möbius function, given by
 $$ \begin{align*} \mu(n) = \begin{cases} (-1)^k &\text{if } n \text{ is the product of } k \text{ distinct primes;}\\ 0 &\text{if } n \text{ is divisible by a square.} \end{cases} \end{align*} $$
$$ \begin{align*} \mu(n) = \begin{cases} (-1)^k &\text{if } n \text{ is the product of } k \text{ distinct primes;}\\ 0 &\text{if } n \text{ is divisible by a square.} \end{cases} \end{align*} $$
This conjecture is wide open in general. However, it has been resolved in a number of special cases [Reference BourgainBou13, Reference Bourgain, Sarnak, Ziegler, Farkas, Gunning, Knopp and TaylorBSZ13, Reference Deshouillers, Drmota and MüllnerDDM15, Reference Downarowicz and KasjanDK15, Reference el Abdalaoui, Kasjan and LemańczykeAKL16, Reference el Abdalaoui, Lemańczyk and de la RueeALdlR14, Reference Ferenczi, Kułaga-Przymus, Lemanczyk, Mauduit, Auslander, Johnson and SilvaFKPLM16, Reference Green and TaoGT12a, Reference GreenGre12, Reference Kułaga-Przymus and LemańczykKPL15, Reference Liu and SarnakLS15, Reference Mauduit and RivatMR10, Reference Mauduit and RivatMR15, Reference MüllnerMül17, Reference PecknerPec18, Reference VeechVee16]; see also the recent survey articles [Reference Drmota, Lemanczyk, Müllner and RivatDLMR, Reference Ferenczi, Kułaga-Przymus, Lemańczyk, Ferenczi, Kułaga-Przymus and LemańczykFKPL18]. Of particular importance to the current paper is Möbius orthogonality for nilsequences [Reference Green and TaoGT12a], which was recently strengthened to short intervals [Reference Matomäki, Shao, Tao and TeräväinenMSTT22]. As we discuss later in this paper, this is closely connected to bracket words thanks to the work of Bergelson and Leibman [Reference Bergelson and LeibmanBL07]. Our second result is the Möbius orthogonality for bracket words along Hardy field functions.
Theorem B. Let
![]() ${\mathbf a} = (a(n))_{n \in \mathbb {Z}}$
be a (two-sided)
${\mathbf a} = (a(n))_{n \in \mathbb {Z}}$
be a (two-sided)
![]() $\mathbb {R}$
-valued bracket word and let
$\mathbb {R}$
-valued bracket word and let
![]() $f \colon \mathbb {R}_+ \to \mathbb {R}$
be a Hardy field function with polynomial growth. Then
$f \colon \mathbb {R}_+ \to \mathbb {R}$
be a Hardy field function with polynomial growth. Then
 $$ \begin{align} \frac{1}{N} \sum_{n=1}^N \mu(n) a(n) \to 0 \quad\text{as } N \to \infty. \end{align} $$
$$ \begin{align} \frac{1}{N} \sum_{n=1}^N \mu(n) a(n) \to 0 \quad\text{as } N \to \infty. \end{align} $$
Remark 1.1. We point out that using similar techniques, it is possible to obtain a slightly stronger result. Firstly, instead of the bracket word, we could work with a bounded generalized polynomial; in fact, each bounded generalized polynomial can be approximated in the supremum norm by finite-valued ones, which allows for a straightforward reduction. Secondly, since all of the key ingredients in the proof of Theorem B are quantitative, one can obtain an explicit rate of convergence to
![]() $0$
in (1). We leave the details to the interested reader.
$0$
in (1). We leave the details to the interested reader.
Theorem B is closely related to Möbius orthogonality for nilsequences, that is, sequences that can be obtained by evaluating a continuous function along an orbit of a point in a nilsystem. The connection between generalized polynomials and nilsequences was established by Bergelson and Leibman [Reference Bergelson and LeibmanBL07], who showed that bounded generalized polynomials can be represented by evaluating a piecewise polynomial function along an orbit in a nilsystem (see Theorem 4.2 for details).
The fact that nilsequences are orthogonal to the Möbius function was established by Green and Tao [Reference Green and TaoGT12a] as a part of their programme of understanding additive patterns in the primes. In fact, [Reference Green and TaoGT12a] already contains an outline of the proof of Möbius orthogonality for bounded generalized polynomials, although some technical details are left out.
In order to obtain a result for a bracket word along a Hardy field function, we split the range of summation into intervals where the Hardy field function under consideration can be efficiently approximated by polynomials. We are then left with the task of establishing cancellation in each of these intervals. A key ingredient is Möbius orthogonality for nilsequences in short intervals, Theorem 5.3, recently established in [Reference Matomäki, Shao, Tao and TeräväinenMSTT22]. The main technical difficulty of our argument lies in extending Theorem 5.3 to piecewise constant (and hence necessarily not continuous) functions with semialgebraic pieces, which we accomplish in §5.2.
1.1 Plan of the paper
In §2 we recall some basic definitions and results about Hardy fields. Moreover, we study Taylor polynomials of functions from a Hardy field generalizing the corresponding part in [Reference Deshouillers, Drmota, Müllner, Shubin and SpiegelhoferDDM+22]. This allows us to locally replace functions from a Hardy field with polynomials. Thus, we need to be able to work with polynomials with varying coefficients. To do so, we study in §3 parametric generalized polynomials, building on and refining results obtained in [Reference Adamczewski and KoniecznyAK23]. These tools allow us to prove Theorem A. In §4 we present some basics on nilmanifolds and discuss the connection to generalized polynomials. Then in §5 we recall a result on Möbius orthogonality for nilsequences in short intervals. This is the final result that we need to prove Theorem B. One naturally arising difficulty is to translate the result on Möbius orthogonality for smooth functions to piecewise polynomial functions.
1.2 Notation
We use
![]() $\mathbb {N} = \{1,2,\dots \}$
to denote the set of positive integers and
$\mathbb {N} = \{1,2,\dots \}$
to denote the set of positive integers and
![]() ${\mathbb {N}_0 = \mathbb {N} \cup \{0\}}$
. For
${\mathbb {N}_0 = \mathbb {N} \cup \{0\}}$
. For
![]() $N \in \mathbb {N}$
, we let
$N \in \mathbb {N}$
, we let
![]() $[N] = \{0,1,\dots ,N-1\}$
. For a non-empty finite set X and a map
$[N] = \{0,1,\dots ,N-1\}$
. For a non-empty finite set X and a map
![]() $f \colon X \to \mathbb {R}$
, we use the symbol
$f \colon X \to \mathbb {R}$
, we use the symbol
![]() $\mathbb {E}$
borrowed from probability theory to denote the average
$\mathbb {E}$
borrowed from probability theory to denote the average
![]() $ \mathbb {E}_{x \in X} f(x) = ({1}/{|X|}) \sum _{x \in X} f(x)$
.
$ \mathbb {E}_{x \in X} f(x) = ({1}/{|X|}) \sum _{x \in X} f(x)$
.
2 Hardy fields
In this section we discuss functions from a Hardy field which have polynomial growth. In particular, we study how the Taylor polynomial of f can be used to describe
![]() $\lfloor f(n) \rfloor $
. Therefore, we first gather some basic results on Hardy fields. Then we discus the uniform distribution of polynomials modulo
$\lfloor f(n) \rfloor $
. Therefore, we first gather some basic results on Hardy fields. Then we discus the uniform distribution of polynomials modulo
![]() $\mathbb {Z}$
. Finally, we study properties of Taylor polynomials and prove the main theorem of this section, namely Theorem 2.11.
$\mathbb {Z}$
. Finally, we study properties of Taylor polynomials and prove the main theorem of this section, namely Theorem 2.11.
2.1 Preliminaries
We start by gathering the basic facts and results on Hardy fields. For further discussion we refer, for example, to [Reference BoshernitzanBos94, Reference FrantzikinakisFra09].
Let
![]() $\mathcal {B}$
be the collection of equivalence classes of real-valued functions defined on some half-line
$\mathcal {B}$
be the collection of equivalence classes of real-valued functions defined on some half-line
![]() $(c, \infty )$
, where we identify two functions if they agree eventually. (The equivalence classes just defined are often called germs of functions. We choose instead to refer to elements of
$(c, \infty )$
, where we identify two functions if they agree eventually. (The equivalence classes just defined are often called germs of functions. We choose instead to refer to elements of
![]() $\mathcal {B}$
as functions, with the understanding that all the operations defined and statements made for elements of
$\mathcal {B}$
as functions, with the understanding that all the operations defined and statements made for elements of
![]() $\mathcal {B}$
are considered only for sufficiently large values of
$\mathcal {B}$
are considered only for sufficiently large values of
![]() $t \in \mathbb {R}$
.) A Hardy field H is a subfield of the ring
$t \in \mathbb {R}$
.) A Hardy field H is a subfield of the ring
![]() $(\mathcal {B}, + , \cdot )$
that is closed under differentiation, meaning that H is a subring of
$(\mathcal {B}, + , \cdot )$
that is closed under differentiation, meaning that H is a subring of
![]() $\mathcal {B}$
such that for each
$\mathcal {B}$
such that for each
![]() $0 \neq f \in H$
, the inverse
$0 \neq f \in H$
, the inverse
![]() $1/f$
exists and belongs to H, f is differentiable and
$1/f$
exists and belongs to H, f is differentiable and
![]() $f' \in H$
. We let
$f' \in H$
. We let
![]() $\mathcal {H}$
denote the union of all Hardy fields. If
$\mathcal {H}$
denote the union of all Hardy fields. If
![]() $f \in \mathcal {H}$
is defined on
$f \in \mathcal {H}$
is defined on
![]() $[0,\infty )$
(one can always choose such a representative of f) we call the sequence
$[0,\infty )$
(one can always choose such a representative of f) we call the sequence
![]() $(f(n))_{n=0}^\infty $
a Hardy sequence.
$(f(n))_{n=0}^\infty $
a Hardy sequence.
We note that choosing different representatives of the same germ of a function f changes the number of subwords of length N of
![]() $a(\lfloor f(n) \rfloor )$
by at most an additive constant. As a consequence, the asymptotic behaviour of the subword complexity of
$a(\lfloor f(n) \rfloor )$
by at most an additive constant. As a consequence, the asymptotic behaviour of the subword complexity of
![]() $a(\lfloor f(n) \rfloor )$
depends only on the germ of f.
$a(\lfloor f(n) \rfloor )$
depends only on the germ of f.
A logarithmic-exponential function is any real-valued function on a half-line
![]() $(c,\infty )$
that can be constructed from the identity map
$(c,\infty )$
that can be constructed from the identity map
![]() $t \mapsto t$
using basic arithmetic operations
$t \mapsto t$
using basic arithmetic operations
![]() $+,-,\times , \div $
, the logarithmic and the exponential functions, and real constants. For example,
$+,-,\times , \div $
, the logarithmic and the exponential functions, and real constants. For example,
![]() $ t^2 + 5t, t^{\sqrt {2}+\sqrt {3}}, e^{(\log t)^2}$
and
$ t^2 + 5t, t^{\sqrt {2}+\sqrt {3}}, e^{(\log t)^2}$
and
![]() $e^{\sqrt {\log t}}/\sqrt {t^2+1}$
are all logarithmic-exponential functions. Every logarithmic-exponential functions belongs to
$e^{\sqrt {\log t}}/\sqrt {t^2+1}$
are all logarithmic-exponential functions. Every logarithmic-exponential functions belongs to
![]() $\mathcal {H}$
, and so do some other classical functions such as
$\mathcal {H}$
, and so do some other classical functions such as
![]() $\Gamma $
,
$\Gamma $
,
![]() $\zeta $
and
$\zeta $
and
![]() $t \mapsto \sin (1/t)$
.
$t \mapsto \sin (1/t)$
.
For real-valued functions f and g on
![]() $(c,\infty )$
such that
$(c,\infty )$
such that
![]() $g(t)$
is non-zero for sufficiently large t, we write
$g(t)$
is non-zero for sufficiently large t, we write
![]() $f(t) \prec g(t)$
if
$f(t) \prec g(t)$
if
![]() $\lim _{t\to \infty } f(t) / g(t) = 0$
,
$\lim _{t\to \infty } f(t) / g(t) = 0$
,
![]() $f(t) \sim g(t)$
if
$f(t) \sim g(t)$
if
![]() $\lim _{t\to \infty } f(t) / g(t)$
is a non-zero real number, and
$\lim _{t\to \infty } f(t) / g(t)$
is a non-zero real number, and
![]() $f(t) \ll g(t)$
if there exists
$f(t) \ll g(t)$
if there exists
![]() $C>0$
such that
$C>0$
such that
![]() $|f(t)| \leq C|g(t)|$
for all large t. For completeness, we let
$|f(t)| \leq C|g(t)|$
for all large t. For completeness, we let
![]() $0 \sim 0$
and
$0 \sim 0$
and
![]() $0 \ll 0$
.
$0 \ll 0$
.
We state the following well-known facts as lemmas.
Lemma 2.1. Let
![]() $f \in \mathcal {H}$
be a function that is not eventually zero. Then f is eventually strictly positive or negative. If f is not eventually constant, then f is eventually strictly monotone.
$f \in \mathcal {H}$
be a function that is not eventually zero. Then f is eventually strictly positive or negative. If f is not eventually constant, then f is eventually strictly monotone.
Proof. Since f is not eventually
![]() $0$
, there exists the inverse function
$0$
, there exists the inverse function
![]() $1/f$
; in particular,
$1/f$
; in particular,
![]() $f(t) \neq 0$
for t large enough. Now, the first part follows from continuity of f. The second part follows directly from the first part by considering
$f(t) \neq 0$
for t large enough. Now, the first part follows from continuity of f. The second part follows directly from the first part by considering
![]() $f'$
.
$f'$
.
Lemma 2.2. Let H be a Hardy field and let
![]() $f,g \in H$
. Then one of the following holds:
$f,g \in H$
. Then one of the following holds:
![]() $f \prec g$
,
$f \prec g$
,
![]() $f \sim g$
or
$f \sim g$
or
![]() $f \succ g$
.
$f \succ g$
.
Proof. If g is eventually zero, the situation is trivial, so assume that this is not the case. Since
![]() $f/g$
is eventually monotone, the limit
$f/g$
is eventually monotone, the limit
![]() $\lim _{t \to \infty } |f(t)|/|g(t)| \in \mathbb {R} \cup \{\infty \}$
exists. If the limit is infinite then
$\lim _{t \to \infty } |f(t)|/|g(t)| \in \mathbb {R} \cup \{\infty \}$
exists. If the limit is infinite then
![]() $f \succ g$
. If the limit is zero then
$f \succ g$
. If the limit is zero then
![]() $f \prec g$
. If the limit is finite and non-zero then
$f \prec g$
. If the limit is finite and non-zero then
![]() $f \sim g$
.
$f \sim g$
.
Definition 2.3. We say that f has polynomial growth if there exists
![]() $n \in \mathbb {N}$
such that
$n \in \mathbb {N}$
such that
![]() ${f(t) \prec t^n}$
.
${f(t) \prec t^n}$
.
We will make use of the following estimates for the derivatives of functions with polynomial growth.
Lemma 2.4. [Reference FrantzikinakisFra09, Lemma 2.1]
Let
![]() $f \in \mathcal {H}$
be a function with polynomial growth. Then at least one of the following statements holds.
$f \in \mathcal {H}$
be a function with polynomial growth. Then at least one of the following statements holds.
-
(i)
 $f(t) \prec t^{-n}$
for all
$f(t) \prec t^{-n}$
for all
 $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
. -
(ii)
 $f(t) \to c \neq 0$
as
$f(t) \to c \neq 0$
as
 $t \to \infty $
for some constant c.
$t \to \infty $
for some constant c. -
(iii)
 $f(t)/(t (\log t)^2)\prec f'(t) \ll f(t)/t$
.
$f(t)/(t (\log t)^2)\prec f'(t) \ll f(t)/t$
.
Lemma 2.5. Let
![]() $f \in \mathcal {H}$
be a function such that
$f \in \mathcal {H}$
be a function such that
![]() $f(t) \prec t^{-n}$
for all
$f(t) \prec t^{-n}$
for all
![]() $n \in \mathbb {N}$
. Then also
$n \in \mathbb {N}$
. Then also
![]() $f^{(\ell )}(n) \prec t^{-n}$
for all
$f^{(\ell )}(n) \prec t^{-n}$
for all
![]() $\ell ,n \in \mathbb {N}$
.
$\ell ,n \in \mathbb {N}$
.
Proof. Reasoning inductively, it is enough to consider the case where
![]() $\ell = 1$
. Suppose, for the sake of contradiction, that
$\ell = 1$
. Suppose, for the sake of contradiction, that
![]() $|f'(t)| \gg t^{-n}$
for some
$|f'(t)| \gg t^{-n}$
for some
![]() $n \in \mathbb {N}$
. Since
$n \in \mathbb {N}$
. Since
![]() $f(t) \to 0$
as
$f(t) \to 0$
as
![]() $t \to \infty $
and since f is eventually monotone, for sufficiently large t we have
$t \to \infty $
and since f is eventually monotone, for sufficiently large t we have
 $$ \begin{align*} |f(t)| = \int_{t}^{\infty} |f'(s)|\, ds \gg \int_{t}^{\infty} s^{-n} \,ds \gg t^{-n+1}, \end{align*} $$
$$ \begin{align*} |f(t)| = \int_{t}^{\infty} |f'(s)|\, ds \gg \int_{t}^{\infty} s^{-n} \,ds \gg t^{-n+1}, \end{align*} $$
contradicting the assumption on f.
Lemma 2.6. Let
![]() $f \in \mathcal {H}$
and assume that
$f \in \mathcal {H}$
and assume that
![]() $f(t) \ll t^{k}$
for some
$f(t) \ll t^{k}$
for some
![]() $k \in \mathbb {Z}$
. Then
$k \in \mathbb {Z}$
. Then
![]() $f^{(\ell )}(t) \ll t^{k-\ell }$
for each
$f^{(\ell )}(t) \ll t^{k-\ell }$
for each
![]() $\ell \in \mathbb {N}$
.
$\ell \in \mathbb {N}$
.
Proof. Reasoning inductively, it is enough to consider the case where
![]() $\ell = 1$
. We consider the three possibilities in Lemma 2.4. If
$\ell = 1$
. We consider the three possibilities in Lemma 2.4. If
![]() $f(t) \prec t^{-n}$
for all
$f(t) \prec t^{-n}$
for all
![]() $n \in \mathbb {N}$
then the claim is trivially true by Lemma 2.5. If
$n \in \mathbb {N}$
then the claim is trivially true by Lemma 2.5. If
![]() $f'(t) \ll f(t)/t$
then
$f'(t) \ll f(t)/t$
then
![]() $f'(t) \ll t^{k-1}$
, as required. Finally, suppose that
$f'(t) \ll t^{k-1}$
, as required. Finally, suppose that
![]() $f(t) \to c \neq 0$
as
$f(t) \to c \neq 0$
as
![]() $n \to \infty $
. Clearly, in this case
$n \to \infty $
. Clearly, in this case
![]() $k \geq 0$
. We may decompose
$k \geq 0$
. We may decompose
![]() ${f(t) = \overline f(t) + c}$
, where
${f(t) = \overline f(t) + c}$
, where
![]() $\overline f(t) = f(t) - c$
and
$\overline f(t) = f(t) - c$
and
![]() $\overline f(t) \prec 1$
. Repeating the reasoning with
$\overline f(t) \prec 1$
. Repeating the reasoning with
![]() $\overline f$
in place of f, we conclude that
$\overline f$
in place of f, we conclude that
![]() $f'(t) = \overline f'(t) \ll t^{-1} \ll t^{k - 1}$
.
$f'(t) = \overline f'(t) \ll t^{-1} \ll t^{k - 1}$
.
Remark 2.7. For each
![]() $f \in \mathcal {H}$
and each logarithmic-exponential function g, there exists a Hardy field H such that
$f \in \mathcal {H}$
and each logarithmic-exponential function g, there exists a Hardy field H such that
![]() $f,g \in H$
(see, for example, [Reference BoshernitzanBos94]). Hence, it follows from Lemma 2.2 that for each
$f,g \in H$
(see, for example, [Reference BoshernitzanBos94]). Hence, it follows from Lemma 2.2 that for each
![]() $f \in \mathcal {H}$
there exists
$f \in \mathcal {H}$
there exists
![]() $k_0(f) \in \mathbb {Z} \cup \{- \infty ,+\infty \}$
such that, for
$k_0(f) \in \mathbb {Z} \cup \{- \infty ,+\infty \}$
such that, for
![]() $k \in \mathbb {Z}$
we have:
$k \in \mathbb {Z}$
we have:
![]() $f(t) \prec t^k$
if
$f(t) \prec t^k$
if
![]() $k> k_0(f)$
,
$k> k_0(f)$
,
![]() $f(t) \succ t^k$
if
$f(t) \succ t^k$
if
![]() $k < k_0(f)$
, and, if
$k < k_0(f)$
, and, if
![]() $k_0(f)$
is finite,
$k_0(f)$
is finite,
![]() ${f(t)\ll t^{k_0(f)}}$
. Lemma 2.6 implies that
${f(t)\ll t^{k_0(f)}}$
. Lemma 2.6 implies that
![]() $k_0(f^{(\ell )}) \leq k_0(f) - \ell $
(with the convention that
$k_0(f^{(\ell )}) \leq k_0(f) - \ell $
(with the convention that
![]() $\pm \infty - \ell = \pm \infty $
).
$\pm \infty - \ell = \pm \infty $
).
2.2 Uniform distribution of polynomials
In this subsection we recall a result about the uniform distribution of polynomials modulo
![]() $\mathbb {Z}$
which we need for the next subsection about Taylor polynomials. It is well known that a polynomial distributes uniformly modulo
$\mathbb {Z}$
which we need for the next subsection about Taylor polynomials. It is well known that a polynomial distributes uniformly modulo
![]() $\mathbb {Z}$
if and only if at least one (non-constant) coefficient is irrational. The following proposition is a quantitative version of this statement.
$\mathbb {Z}$
if and only if at least one (non-constant) coefficient is irrational. The following proposition is a quantitative version of this statement.
First we need to specify the way we quantify how uniformly distributed a sequence
![]() $a(n) \bmod \mathbb {Z}$
is. Let
$a(n) \bmod \mathbb {Z}$
is. Let
![]() $( x_1, \ldots , x_N )$
be a finite sequence of real numbers. Its discrepancy is defined by
$( x_1, \ldots , x_N )$
be a finite sequence of real numbers. Its discrepancy is defined by
 $$ \begin{align} D_N (x_1, \ldots, x_N) = \sup_{0 \le \alpha \le \beta \le 1} \bigg| \frac{\# \{ n \le N : \alpha \le \{ x_n \} < \beta \}}{N} - (\beta - \alpha) \bigg|. \end{align} $$
$$ \begin{align} D_N (x_1, \ldots, x_N) = \sup_{0 \le \alpha \le \beta \le 1} \bigg| \frac{\# \{ n \le N : \alpha \le \{ x_n \} < \beta \}}{N} - (\beta - \alpha) \bigg|. \end{align} $$
Thus, we have the necessary prerequisites to state the following proposition.
Proposition 2.8. [Reference Deshouillers, Drmota, Müllner, Shubin and SpiegelhoferDDM+22, Proposition 5.2]
Suppose that
![]() $g: \mathbb {Z} \to \mathbb {R}$
is a polynomial of degree d, which we write as
$g: \mathbb {Z} \to \mathbb {R}$
is a polynomial of degree d, which we write as
Furthermore, let
![]() $\delta \in (0,1/2)$
. Then either the discrepancy of
$\delta \in (0,1/2)$
. Then either the discrepancy of
![]() $(g(n) \bmod \mathbb {Z})_{n\in [N]}$
is smaller than
$(g(n) \bmod \mathbb {Z})_{n\in [N]}$
is smaller than
![]() $\delta $
, or else there is an integer
$\delta $
, or else there is an integer
![]() $1\leq \ell \ll \delta ^{-O_d(1)}$
such that
$1\leq \ell \ll \delta ^{-O_d(1)}$
such that
This proposition is a direct consequence of [Reference Green and TaoGT12b, Proposition 4.3], who attribute this result to Weyl.
2.3 Taylor expansions
For any germ
![]() $f \in \mathcal {H}$
we consider a representative that is defined on
$f \in \mathcal {H}$
we consider a representative that is defined on
![]() $[1,\infty )$
and also call it f. Then, for any
$[1,\infty )$
and also call it f. Then, for any
![]() $x \in (1,\infty )$
and
$x \in (1,\infty )$
and
![]() $\ell \in \mathbb {N}_0$
, we can consider the length-
$\ell \in \mathbb {N}_0$
, we can consider the length-
![]() $\ell $
Taylor expansion of f at the point x,
$\ell $
Taylor expansion of f at the point x,
 $$ \begin{align} \!\!\!\!\!\!\!\!\!P_{x,\ell}(y) &:= f(x) + y f'(x) + \cdots + \frac{y^{\ell-1}}{(\ell-1)!} f^{(\ell-1)}(x), \end{align} $$
$$ \begin{align} \!\!\!\!\!\!\!\!\!P_{x,\ell}(y) &:= f(x) + y f'(x) + \cdots + \frac{y^{\ell-1}}{(\ell-1)!} f^{(\ell-1)}(x), \end{align} $$
Proposition 2.9. Let
![]() $k \in \mathbb {Z}$
,
$k \in \mathbb {Z}$
,
![]() $\ell \in \mathbb {N}_0$
, and let
$\ell \in \mathbb {N}_0$
, and let
![]() $f \in \mathcal {H}$
be a function with
$f \in \mathcal {H}$
be a function with
![]() $f(t) \ll t^{k}$
. Then the error term
$f(t) \ll t^{k}$
. Then the error term
![]() $R_{x,\ell }(y)$
in the Taylor expansion (3)–(5) satisfies
$R_{x,\ell }(y)$
in the Taylor expansion (3)–(5) satisfies
uniformly for all
![]() $x\geq 1$
and
$x\geq 1$
and
![]() $0\leq y \leq x$
, where the implied constant only depends on f and
$0\leq y \leq x$
, where the implied constant only depends on f and
![]() $\ell $
.
$\ell $
.
Proof. Combining (5) and Lemma 2.6. we have
 $$ \begin{align*} y^{-\ell} R_{x,\ell}(y) \ll \sup_{\xi \in [0,y]} f^{(\ell)}(x+\xi) \ll \sup_{\xi \in [0,y]} (x+\xi)^{k-\ell} = \begin{cases} x^{k-\ell} & \text{if } k < \ell,\\ (x+y)^{k-\ell} & \text{if } k \geq \ell. \end{cases} \end{align*} $$
$$ \begin{align*} y^{-\ell} R_{x,\ell}(y) \ll \sup_{\xi \in [0,y]} f^{(\ell)}(x+\xi) \ll \sup_{\xi \in [0,y]} (x+\xi)^{k-\ell} = \begin{cases} x^{k-\ell} & \text{if } k < \ell,\\ (x+y)^{k-\ell} & \text{if } k \geq \ell. \end{cases} \end{align*} $$
Assuming that
![]() $x \geq y$
, the two estimates are equivalent.
$x \geq y$
, the two estimates are equivalent.
Lemma 2.10. Let
![]() $k \in \mathbb {N}$
and let f be a k times continuously differentiable function defined on an open interval
$k \in \mathbb {N}$
and let f be a k times continuously differentiable function defined on an open interval
![]() $I \subseteq \mathbb {R}$
. Suppose that
$I \subseteq \mathbb {R}$
. Suppose that
![]() $f^{(k)}(t)$
has constant sign on I. Then f changes monotonicity on I at most
$f^{(k)}(t)$
has constant sign on I. Then f changes monotonicity on I at most
![]() $k-1$
times.
$k-1$
times.
Proof. If
![]() $f^{(k)}(t)$
is constant zero for all
$f^{(k)}(t)$
is constant zero for all
![]() $t \in I$
, then f is a polynomial of degree at most
$t \in I$
, then f is a polynomial of degree at most
![]() $k-1$
and the statement is trivially true. Thus, we assume without loss of generality that
$k-1$
and the statement is trivially true. Thus, we assume without loss of generality that
![]() $f^{(k)}(t)> 0$
for all
$f^{(k)}(t)> 0$
for all
![]() $t \in I$
. Let us assume for the sake of contradiction that f changes monotonicity at least k times. Thus,
$t \in I$
. Let us assume for the sake of contradiction that f changes monotonicity at least k times. Thus,
![]() $f'$
has at least k zeros in I. It follows from the mean value theorem that
$f'$
has at least k zeros in I. It follows from the mean value theorem that
![]() $f"$
has at least
$f"$
has at least
![]() $k-1$
zeros in I. Inductively applying this reasoning shows that
$k-1$
zeros in I. Inductively applying this reasoning shows that
![]() $f^{(k)}$
has at least one zero in I, giving the desired contradiction.
$f^{(k)}$
has at least one zero in I, giving the desired contradiction.
Theorem 2.11. Let
![]() $k,\ell \in \mathbb {N}$
be integers with
$k,\ell \in \mathbb {N}$
be integers with
![]() $k < \ell $
, and let
$k < \ell $
, and let
![]() $f \in \mathcal {H}$
be a function satisfying
$f \in \mathcal {H}$
be a function satisfying
![]() $f(t) \ll t^{k}$
, and let
$f(t) \ll t^{k}$
, and let
![]() $P_{N,\ell }$
and
$P_{N,\ell }$
and
![]() $R_{N,\ell }$
be given by (3)–(5). Then there exists some
$R_{N,\ell }$
be given by (3)–(5). Then there exists some
![]() $0<\eta <1$
(only depending on
$0<\eta <1$
(only depending on
![]() $\ell $
) such that for any
$\ell $
) such that for any
![]() $H \in \mathbb {N}$
, the formula
$H \in \mathbb {N}$
, the formula
defines at most
![]() $\exp (O(H^{\eta }))$
different functions
$\exp (O(H^{\eta }))$
different functions
![]() $e_{N}: [H] \to \mathbb {Z}$
for
$e_{N}: [H] \to \mathbb {Z}$
for
![]() $N \in \mathbb {N}$
. Moreover, for each N, at least one of the following statements holds.
$N \in \mathbb {N}$
. Moreover, for each N, at least one of the following statements holds.
-
(i) N is small:
 $N = O(H^{( \ell + \eta )/( \ell - k )})$
.
$N = O(H^{( \ell + \eta )/( \ell - k )})$
. -
(ii)
 $e_N$
is sparse: there are at most
$e_N$
is sparse: there are at most
 $O(H^{\eta })$
values of
$O(H^{\eta })$
values of
 $h \in [H]$
such that
$h \in [H]$
such that
 $e_N(h) \neq 0$
.
$e_N(h) \neq 0$
. -
(iii)
 $e_N$
is structured: there exists a partition of
$e_N$
is structured: there exists a partition of
 $[H]$
into
$[H]$
into
 $O(H^{\eta })$
arithmetic progressions with step
$O(H^{\eta })$
arithmetic progressions with step
 $O(H^{\eta })$
on which
$O(H^{\eta })$
on which
 $e_N$
is constant.
$e_N$
is constant.
(In the theorem above, the constants implicit in the
![]() $O(\cdot )$
notation are allowed to depend on
$O(\cdot )$
notation are allowed to depend on
![]() $k,\ell $
and f.)
$k,\ell $
and f.)
Proof. We define
![]() $\varepsilon = H^{-\eta _0}$
for some
$\varepsilon = H^{-\eta _0}$
for some
![]() $\eta _0> 0$
which only depends on
$\eta _0> 0$
which only depends on
![]() $\ell $
and will be specified later. Let
$\ell $
and will be specified later. Let
![]() $N \in \mathbb {N}$
. Recall that by Proposition 2.9, we have
$N \in \mathbb {N}$
. Recall that by Proposition 2.9, we have
unless
![]() $N \ll \varepsilon ^{-{1}/( \ell -k ) }H^{{\ell }/( \ell - k )} = H^{( \ell + \eta _0 )/( \ell -k )}$
. Thus, the values of N such that (7) is false contribute only
$N \ll \varepsilon ^{-{1}/( \ell -k ) }H^{{\ell }/( \ell - k )} = H^{( \ell + \eta _0 )/( \ell -k )}$
. Thus, the values of N such that (7) is false contribute only
![]() $O( H^{O(1)} )$
different sequences
$O( H^{O(1)} )$
different sequences
![]() $e_N$
, and we may freely assume that N is large enough that (7) holds. In this case we have
$e_N$
, and we may freely assume that N is large enough that (7) holds. In this case we have
![]() $e_N: [H] \to \{-1,0,1\}$
. Additionally, by Lemma 2.1 we may also assume that
$e_N: [H] \to \{-1,0,1\}$
. Additionally, by Lemma 2.1 we may also assume that
![]() $f^{(\ell )}(x) \neq 0$
for all
$f^{(\ell )}(x) \neq 0$
for all
![]() $x \geq N$
. As a consequence of (7), for each
$x \geq N$
. As a consequence of (7), for each
![]() $0 \leq h < H$
, if
$0 \leq h < H$
, if
then ⌊f(N + h)⌋ = ⌊P
N, ℓ
(h)⌋ and hence
![]() $e_N(h) = 0$
.
$e_N(h) = 0$
.
Let
![]() $\alpha _0,\dots ,\alpha _{\ell -1}$
denote the coefficients of
$\alpha _0,\dots ,\alpha _{\ell -1}$
denote the coefficients of
![]() $P_{N,\ell }$
:
$P_{N,\ell }$
:
By Proposition 2.8, we distinguish two cases.
-
(I)
 $(P_{N,\ell }(h))_{h \in [H]}$
has discrepancy at most
$(P_{N,\ell }(h))_{h \in [H]}$
has discrepancy at most
 $\varepsilon $
.
$\varepsilon $
. -
(II) There exists
 $1\leq q \ll \varepsilon ^{-O(1)}$
such that
$1\leq q \ll \varepsilon ^{-O(1)}$
such that
 $\max _{0 \leq j < \ell } H^j\lVert q \alpha _j \rVert \ll \varepsilon ^{-O(1)}$
.
$\max _{0 \leq j < \ell } H^j\lVert q \alpha _j \rVert \ll \varepsilon ^{-O(1)}$
.
In the first case, it follows that the number of
![]() $h \in [H]$
such that (8) does not hold is at most
$h \in [H]$
such that (8) does not hold is at most
![]() ${3}\varepsilon H$
. Thus,
${3}\varepsilon H$
. Thus,
![]() $e_{N}$
is sparse, that is, it has at most
$e_{N}$
is sparse, that is, it has at most
![]() ${3}\varepsilon H \ll H^{1-\eta _0}$
non-zero entries. It remains to estimate the number of the sequences
${3}\varepsilon H \ll H^{1-\eta _0}$
non-zero entries. It remains to estimate the number of the sequences
![]() $e_N$
of this type. Using a standard estimate
$e_N$
of this type. Using a standard estimate
![]() $\binom {n}{k} \leq n^k/k! < (en)^k/k^k$
, we find
$\binom {n}{k} \leq n^k/k! < (en)^k/k^k$
, we find
 $$ \begin{align*} \log \left( \sum_{0\leq j \leq 3 \varepsilon H} \binom{H}{j} 2^j \right) & \ll \log ( 3\varepsilon H ) + \log \binom{H}{ 3 \varepsilon H} + 3 \varepsilon H \\ & \ll \log(3 H^{1-\eta_0}) + 3 \varepsilon H \log(e 3 H^{1-\eta_0}) + 3 H^{1-\eta_0}\\ &\ll_{\eta_0} H^{1-\eta_0/2}. \end{align*} $$
$$ \begin{align*} \log \left( \sum_{0\leq j \leq 3 \varepsilon H} \binom{H}{j} 2^j \right) & \ll \log ( 3\varepsilon H ) + \log \binom{H}{ 3 \varepsilon H} + 3 \varepsilon H \\ & \ll \log(3 H^{1-\eta_0}) + 3 \varepsilon H \log(e 3 H^{1-\eta_0}) + 3 H^{1-\eta_0}\\ &\ll_{\eta_0} H^{1-\eta_0/2}. \end{align*} $$
Thus the number of distinct sequences
![]() $e_N$
is bounded by
$e_N$
is bounded by
![]() $\exp (O(H^{1-\eta _0/2}))$
, which gives the desired result as long as
$\exp (O(H^{1-\eta _0/2}))$
, which gives the desired result as long as
![]() $1-\eta _0/2\leq \eta $
.
$1-\eta _0/2\leq \eta $
.
In the second case we split
![]() $[H]$
into arithmetic progressions with common difference
$[H]$
into arithmetic progressions with common difference
![]() $q \ll \varepsilon ^{-O_{\ell }(1)}$
. This allows us to write (for
$q \ll \varepsilon ^{-O_{\ell }(1)}$
. This allows us to write (for
![]() $0\leq m < q$
)
$0\leq m < q$
)
 $$ \begin{align*} P_{N,\ell}(q h + m) &= \alpha_{0} + (q h + m) \alpha_{1} + \cdots + (q h + m)^{\ell-1} \alpha_{\ell-1}\\ &= \beta_{0} + h \beta_{1} + \cdots + h^{\ell-1}\beta_{\ell-1}. \end{align*} $$
$$ \begin{align*} P_{N,\ell}(q h + m) &= \alpha_{0} + (q h + m) \alpha_{1} + \cdots + (q h + m)^{\ell-1} \alpha_{\ell-1}\\ &= \beta_{0} + h \beta_{1} + \cdots + h^{\ell-1}\beta_{\ell-1}. \end{align*} $$
The defining property of q implies that
In particular, we can write
where
![]() $z_{j} \in \mathbb {Z}$
and
$z_{j} \in \mathbb {Z}$
and
![]() $|s_{j}| \ll H^{-j} \cdot \varepsilon ^{-O_{\ell }(1)}$
for
$|s_{j}| \ll H^{-j} \cdot \varepsilon ^{-O_{\ell }(1)}$
for
![]() $ 0 \leq j < \ell $
. Putting everything together, we find
$ 0 \leq j < \ell $
. Putting everything together, we find
where
 $$ \begin{align*} Q(h) &= z_{0} + h z_{1} + \cdots + h^{\ell-1} z_{\ell-1},\\ r(h) &= s_{0} + h s_{1} + \cdots + h^{\ell-1} s_{\ell-1}. \end{align*} $$
$$ \begin{align*} Q(h) &= z_{0} + h z_{1} + \cdots + h^{\ell-1} z_{\ell-1},\\ r(h) &= s_{0} + h s_{1} + \cdots + h^{\ell-1} s_{\ell-1}. \end{align*} $$
In particular, Q is a polynomial of degree at most
![]() $\ell -1$
with integer coefficients and
$\ell -1$
with integer coefficients and
![]() $P_{N, \ell }(q h +m) = Q(h) + r(h)$
. Moreover,
$P_{N, \ell }(q h +m) = Q(h) + r(h)$
. Moreover,
![]() $|r(h)| \ll \varepsilon ^{-O_{\ell }(1)}$
for all
$|r(h)| \ll \varepsilon ^{-O_{\ell }(1)}$
for all
![]() $h \in [0,H/q]$
. Since
$h \in [0,H/q]$
. Since
![]() $|R_{N,\ell }(h)| \leq \varepsilon $
, we see that
$|R_{N,\ell }(h)| \leq \varepsilon $
, we see that
holds exactly if either
 $$ \begin{align} \begin{split} \{r(h) \} \leq \varepsilon \quad &\text{and} \quad \{r(h) + R_{N,\ell}(q h + m) \} \geq 1-\varepsilon,\quad \text{or}\\\{r(h) \} \geq 1-\varepsilon \quad &\text{and} \quad \{r(h) + R_{N,\ell}(q h + m) \} \leq \varepsilon. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \{r(h) \} \leq \varepsilon \quad &\text{and} \quad \{r(h) + R_{N,\ell}(q h + m) \} \geq 1-\varepsilon,\quad \text{or}\\\{r(h) \} \geq 1-\varepsilon \quad &\text{and} \quad \{r(h) + R_{N,\ell}(q h + m) \} \leq \varepsilon. \end{split} \end{align} $$
In the first case
![]() $e_N(q h +m) = 1$
and in the second case
$e_N(q h +m) = 1$
and in the second case
![]() $e_N(q h + m) = -1$
. Since
$e_N(q h + m) = -1$
. Since
![]() $r(h)$
is a polynomial of degree at most
$r(h)$
is a polynomial of degree at most
![]() $\ell -1$
, it changes monotonicity at most
$\ell -1$
, it changes monotonicity at most
![]() $\ell - 2$
times. Since the
$\ell - 2$
times. Since the
![]() $\ell $
th derivative of
$\ell $
th derivative of
![]() $r(h) + R_{N,\ell }(q h + m) = f(N + q h + m) - P_{N,\ell }(q h + m) + r(h)$
has constant sign, by Lemma 2.10 it changes monotonicity at most
$r(h) + R_{N,\ell }(q h + m) = f(N + q h + m) - P_{N,\ell }(q h + m) + r(h)$
has constant sign, by Lemma 2.10 it changes monotonicity at most
![]() $\ell -1$
times on the interval
$\ell -1$
times on the interval
![]() $[0, H/q]$
. Hence, we can decompose
$[0, H/q]$
. Hence, we can decompose
![]() $[0, H/q]$
into at most
$[0, H/q]$
into at most
![]() $2 \ell -2$
intervals
$2 \ell -2$
intervals
![]() $I_1, \ldots , I_p$
on which
$I_1, \ldots , I_p$
on which
![]() $r(h)$
and
$r(h)$
and
![]() $r(h) + R_{N,\ell }(q h + m)$
are both monotone. As
$r(h) + R_{N,\ell }(q h + m)$
are both monotone. As
![]() $|r(h)| \ll \varepsilon ^{-O_{\ell }(1)}$
, we can further subdivide each of the intervals
$|r(h)| \ll \varepsilon ^{-O_{\ell }(1)}$
, we can further subdivide each of the intervals
![]() $I_j$
into
$I_j$
into
![]() $O(\varepsilon ^{-O_{\ell }(1)})$
subintervals such that for each subinterval, each of the inequalities is either true on the entire subinterval or false on the entire subinterval. As a consequence,
$O(\varepsilon ^{-O_{\ell }(1)})$
subintervals such that for each subinterval, each of the inequalities is either true on the entire subinterval or false on the entire subinterval. As a consequence,
![]() $e_N$
is structured, that is,
$e_N$
is structured, that is,
![]() $e_N$
is constant on each subinterval. Thus, we have found a decomposition of
$e_N$
is constant on each subinterval. Thus, we have found a decomposition of
![]() $[H]$
into
$[H]$
into
![]() $O(\varepsilon ^{-O_{\ell }(1)})$
arithmetic progressions on which
$O(\varepsilon ^{-O_{\ell }(1)})$
arithmetic progressions on which
![]() $e_N$
is constant. We can write
$e_N$
is constant. We can write
![]() $O(\varepsilon ^{-O_{\ell }(1)}) = O(H^{C \eta _0})$
for some
$O(\varepsilon ^{-O_{\ell }(1)}) = O(H^{C \eta _0})$
for some
![]() $C = C(\ell )>0$
. Using the rough estimate
$C = C(\ell )>0$
. Using the rough estimate
![]() $H^3$
for the number of arithmetic sequences contained in
$H^3$
for the number of arithmetic sequences contained in
![]() $[H]$
, we can bound the number of sequences
$[H]$
, we can bound the number of sequences
![]() $e_N$
which arise this way by
$e_N$
which arise this way by
It remains to choose
![]() $\eta _0 = (C+2)^{-1}$
and
$\eta _0 = (C+2)^{-1}$
and
![]() $\eta = 1-(2(C+2))^{-1}$
to finish the proof.
$\eta = 1-(2(C+2))^{-1}$
to finish the proof.
3 Parametric generalized polynomials
In this section we discuss parametric generalized polynomials, building on and refining results obtained in [Reference Adamczewski and KoniecznyAK23]. In particular, we show that for any parametrized general polynomial that takes values in
![]() $[M]$
, we can assume that the parameters belong to
$[M]$
, we can assume that the parameters belong to
![]() $[0,1)^J$
for some finite set J (Proposition 3.5). This allows us to show a polynomial bound on the number of subwords of bracket words along polynomials of a fixed degree (Corollary 3.7). At the end of the section we give the proof of Theorem A.
$[0,1)^J$
for some finite set J (Proposition 3.5). This allows us to show a polynomial bound on the number of subwords of bracket words along polynomials of a fixed degree (Corollary 3.7). At the end of the section we give the proof of Theorem A.
Let
![]() $d \in \mathbb {N}$
. Generalized polynomial (GP) maps from
$d \in \mathbb {N}$
. Generalized polynomial (GP) maps from
![]() $\mathbb {R}^d$
to
$\mathbb {R}^d$
to
![]() $\mathbb {R}$
are the smallest family
$\mathbb {R}$
are the smallest family
![]() $\mathcal {G}$
such that (1) all polynomial maps belong to
$\mathcal {G}$
such that (1) all polynomial maps belong to
![]() $\mathcal {G}$
; (2) if
$\mathcal {G}$
; (2) if
![]() $g,h \in \mathcal {G}$
then also
$g,h \in \mathcal {G}$
then also
![]() $ g + h, g \cdot h \in \mathcal {G}$
(with operations defined pointwise); (3) if
$ g + h, g \cdot h \in \mathcal {G}$
(with operations defined pointwise); (3) if
![]() $g \in \mathcal {G}$
then also
$g \in \mathcal {G}$
then also
![]() $\lfloor g \rfloor \in \mathcal {G}$
, where
$\lfloor g \rfloor \in \mathcal {G}$
, where
![]() $\lfloor g \rfloor $
is defined pointwise by
$\lfloor g \rfloor $
is defined pointwise by
![]() $\lfloor g \rfloor (x) = \lfloor g(x) \rfloor $
. We note that GP maps are also closed under the operation of taking the fractional part, given by
$\lfloor g \rfloor (x) = \lfloor g(x) \rfloor $
. We note that GP maps are also closed under the operation of taking the fractional part, given by
![]() $\{ g \} = g - \lfloor g \rfloor $
. For sets
$\{ g \} = g - \lfloor g \rfloor $
. For sets
![]() $\Omega \subseteq \mathbb {R}^d$
and
$\Omega \subseteq \mathbb {R}^d$
and
![]() $\Sigma \subseteq \mathbb {R}$
(for example,
$\Sigma \subseteq \mathbb {R}$
(for example,
![]() $\Omega = \mathbb {Z}^d$
,
$\Omega = \mathbb {Z}^d$
,
![]() $\Sigma = \mathbb {Z}$
), by a GP map
$\Sigma = \mathbb {Z}$
), by a GP map
![]() $g \colon \Omega \to \Sigma $
we mean the restriction
$g \colon \Omega \to \Sigma $
we mean the restriction
![]() $\widetilde g|_{\Omega }$
to
$\widetilde g|_{\Omega }$
to
![]() $\Omega $
of a GP map
$\Omega $
of a GP map
![]() $\widetilde g \colon \mathbb {R}^d \to \mathbb {R}$
such that
$\widetilde g \colon \mathbb {R}^d \to \mathbb {R}$
such that
![]() $\widetilde g(\Omega ) \subseteq \Sigma $
. We point out that, unlike in the case of polynomials, the lift
$\widetilde g(\Omega ) \subseteq \Sigma $
. We point out that, unlike in the case of polynomials, the lift
![]() $\widetilde g$
is not uniquely determined by g, unless
$\widetilde g$
is not uniquely determined by g, unless
![]() $\Omega = \mathbb {R}^d$
.
$\Omega = \mathbb {R}^d$
.
In [Reference Adamczewski and KoniecznyAK23], we introduced the notion of a parametric GP map
![]() $\mathbb {Z} \to \mathbb {R}$
with a finite index set I, which (modulo some notational conventions) is essentially the same as a GP map
$\mathbb {Z} \to \mathbb {R}$
with a finite index set I, which (modulo some notational conventions) is essentially the same as a GP map
![]() $\mathbb {R}^I \times \mathbb {Z} \to \mathbb {R}$
. For instance, the formula
$\mathbb {R}^I \times \mathbb {Z} \to \mathbb {R}$
. For instance, the formula
defines a GP map
![]() $\mathbb {Z} \to \mathbb {R}$
(or, strictly speaking, a family of GP maps) parametrized by
$\mathbb {Z} \to \mathbb {R}$
(or, strictly speaking, a family of GP maps) parametrized by
![]() $\mathbb {R}^2$
. Formally, a parametric GP map with index set I or a GP map parametrized by
$\mathbb {R}^2$
. Formally, a parametric GP map with index set I or a GP map parametrized by
![]() $\mathbb {R}^I$
is a map
$\mathbb {R}^I$
is a map
![]() $\mathbb {R}^I \to \mathbb {R}^{\mathbb {Z}}$
,
$\mathbb {R}^I \to \mathbb {R}^{\mathbb {Z}}$
,
![]() $\alpha \mapsto g_\alpha $
, such that the combined map
$\alpha \mapsto g_\alpha $
, such that the combined map
![]() $\mathbb {R}^I \times \mathbb {Z} \to \mathbb {R}$
,
$\mathbb {R}^I \times \mathbb {Z} \to \mathbb {R}$
,
![]() $(\alpha ,n) \mapsto g_\alpha (n)$
, is a GP map.
$(\alpha ,n) \mapsto g_\alpha (n)$
, is a GP map.
Here we will need a marginally more precise notion, where the set of parameters takes the form
![]() $\mathbb {R}^{I_{\mathrm {real}}} \times \mathbb {Z}^{I_{\mathrm {int}}} \times [0,1)^{I_{\mathrm {frac}}}$
rather than
$\mathbb {R}^{I_{\mathrm {real}}} \times \mathbb {Z}^{I_{\mathrm {int}}} \times [0,1)^{I_{\mathrm {frac}}}$
rather than
![]() $\mathbb {R}^I$
. Let
$\mathbb {R}^I$
. Let
![]() $I_{\mathrm {real}}, I_{\mathrm {int}}, I_{\mathrm {frac}}$
be pairwise disjoint finite sets and put
$I_{\mathrm {real}}, I_{\mathrm {int}}, I_{\mathrm {frac}}$
be pairwise disjoint finite sets and put
![]() $I = I_{\mathrm {real}} \cup I_{\mathrm {int}} \cup I_{\mathrm {frac}}$
. Then a GP map parametrized by
$I = I_{\mathrm {real}} \cup I_{\mathrm {int}} \cup I_{\mathrm {frac}}$
. Then a GP map parametrized by
![]() $\mathbb {R}^{I_{\mathrm {real}}} \times \mathbb {Z}^{I_{\mathrm {int}}} \times [0,1)^{I_{\mathrm {frac}}}$
is the restriction of a GP map parametrized by
$\mathbb {R}^{I_{\mathrm {real}}} \times \mathbb {Z}^{I_{\mathrm {int}}} \times [0,1)^{I_{\mathrm {frac}}}$
is the restriction of a GP map parametrized by
![]() $\mathbb {R}^{I_{\mathrm {real}}} \times \mathbb {R}^{I_{\mathrm {int}}} \times \mathbb {R}^{I_{\mathrm {frac}}}$
(as defined above) to
$\mathbb {R}^{I_{\mathrm {real}}} \times \mathbb {R}^{I_{\mathrm {int}}} \times \mathbb {R}^{I_{\mathrm {frac}}}$
(as defined above) to
![]() $\mathbb {R}^{I_{\mathrm {real}}} \times \mathbb {Z}^{I_{\mathrm {int}}} \times [0,1)^{I_{\mathrm {frac}}}$
. We note that in the case where
$\mathbb {R}^{I_{\mathrm {real}}} \times \mathbb {Z}^{I_{\mathrm {int}}} \times [0,1)^{I_{\mathrm {frac}}}$
. We note that in the case where
![]() $I_{\mathrm {int}} = I_{\mathrm {frac}} = \emptyset $
, the new definition is consistent with the previous one.
$I_{\mathrm {int}} = I_{\mathrm {frac}} = \emptyset $
, the new definition is consistent with the previous one.
In [Reference Adamczewski and KoniecznyAK23] we defined the operations of addition, multiplication and the integer part for parametric GP maps, not necessarily indexed by the same set. Roughly speaking, if
![]() $I \subseteq J$
are finite sets then we can always think of a GP map parametrized by
$I \subseteq J$
are finite sets then we can always think of a GP map parametrized by
![]() $\mathbb {R}^I$
as a GP map parametrized by
$\mathbb {R}^I$
as a GP map parametrized by
![]() $\mathbb {R}^J$
, with trivial dependence on the parameters in
$\mathbb {R}^J$
, with trivial dependence on the parameters in
![]() $\mathbb {R}^{J \setminus I}$
. Thus, if
$\mathbb {R}^{J \setminus I}$
. Thus, if
![]() $g_{\bullet }$
and
$g_{\bullet }$
and
![]() $h_{\bullet }$
are GP maps parametrized by
$h_{\bullet }$
are GP maps parametrized by
![]() $\mathbb {R}^I$
and
$\mathbb {R}^I$
and
![]() $\mathbb {R}^J$
respectively, then we can think of both
$\mathbb {R}^J$
respectively, then we can think of both
![]() $g_{\bullet }$
and
$g_{\bullet }$
and
![]() $h_{\bullet }$
as GP maps parametrized by
$h_{\bullet }$
as GP maps parametrized by
![]() $\mathbb {R}^{I \cup J}$
, which gives us a natural way to define the (pointwise) sum and product
$\mathbb {R}^{I \cup J}$
, which gives us a natural way to define the (pointwise) sum and product
![]() $g_{\bullet } + h_{\bullet }$
and
$g_{\bullet } + h_{\bullet }$
and
![]() $g_{\bullet } \cdot h_{\bullet }$
. We refer to [Reference Adamczewski and KoniecznyAK23] for a formal definition. This construction directly extends to GP maps parametrized by
$g_{\bullet } \cdot h_{\bullet }$
. We refer to [Reference Adamczewski and KoniecznyAK23] for a formal definition. This construction directly extends to GP maps parametrized by
![]() $\mathbb {R}^{I_{\mathrm {real}}} \times \mathbb {Z}^{I_{\mathrm {int}}} \times [0,1)^{I_{\mathrm {frac}}}$
.
$\mathbb {R}^{I_{\mathrm {real}}} \times \mathbb {Z}^{I_{\mathrm {int}}} \times [0,1)^{I_{\mathrm {frac}}}$
.
Definition 3.1. Let
![]() $g_\bullet $
and
$g_\bullet $
and
![]() $h_\bullet $
be two GP maps parametrized by
$h_\bullet $
be two GP maps parametrized by
![]() $\mathbb {R}^{I_{\mathrm {real}}} \times \mathbb {Z}^{I_{\mathrm {int}}} \times [0,1)^{I_{\mathrm {frac}}}$
and
$\mathbb {R}^{I_{\mathrm {real}}} \times \mathbb {Z}^{I_{\mathrm {int}}} \times [0,1)^{I_{\mathrm {frac}}}$
and
![]() $\mathbb {R}^{J_{\mathrm {real}}} \times \mathbb {Z}^{J_{\mathrm {int}}} \times [0,1)^{J_{\mathrm {frac}}}$
, respectively. Then we say that
$\mathbb {R}^{J_{\mathrm {real}}} \times \mathbb {Z}^{J_{\mathrm {int}}} \times [0,1)^{J_{\mathrm {frac}}}$
, respectively. Then we say that
![]() $h_\bullet $
extends
$h_\bullet $
extends
![]() $g_\bullet $
, denoted
$g_\bullet $
, denoted
![]() ${h_\bullet \succeq g_\bullet }$
, if there exists a GP map
${h_\bullet \succeq g_\bullet }$
, if there exists a GP map
![]() $\varphi \colon \mathbb {R}^{I_{\mathrm {real}}} \times \mathbb {R}^{I_{\mathrm {int}}} \times \mathbb {R}^{I_{\mathrm {frac}}} \to \mathbb {R}^{J_{\mathrm {real}}} \times \mathbb {R}^{J_{\mathrm {int}}} \times \mathbb {R}^{J_{\mathrm {frac}}}$
such that
$\varphi \colon \mathbb {R}^{I_{\mathrm {real}}} \times \mathbb {R}^{I_{\mathrm {int}}} \times \mathbb {R}^{I_{\mathrm {frac}}} \to \mathbb {R}^{J_{\mathrm {real}}} \times \mathbb {R}^{J_{\mathrm {int}}} \times \mathbb {R}^{J_{\mathrm {frac}}}$
such that
-
• φ(ℝ I real × ℤ I int × [0, 1) I frac ) ⊆ ℝ I real × ℤ I int × [0, 1) I frac , and
-
• g α = h φ(α) for all α ∈ ℝ I real × ℤ I int × [0, 1) I frac .
We use different notation
![]() $h_\bullet \succeq g_\bullet $
than in [Reference Adamczewski and KoniecznyAK23] in order to avoid confusion with the symbol
$h_\bullet \succeq g_\bullet $
than in [Reference Adamczewski and KoniecznyAK23] in order to avoid confusion with the symbol
![]() $\succ $
extensively used in §2. In [Reference Adamczewski and KoniecznyAK23] we obtained a polynomial bound on the number of possible prefixes of a given GP map parametrized by
$\succ $
extensively used in §2. In [Reference Adamczewski and KoniecznyAK23] we obtained a polynomial bound on the number of possible prefixes of a given GP map parametrized by
![]() $[0,1)^I$
.
$[0,1)^I$
.
Theorem 3.2. [Reference Adamczewski and KoniecznyAK23, Theorem 15.3]
Let
![]() $g_\bullet :\mathbb {Z} \to \mathbb {Z}$
be a GP map parametrized by
$g_\bullet :\mathbb {Z} \to \mathbb {Z}$
be a GP map parametrized by
![]() $[0,1)^I$
for some finite set I. Then there exists a constant C such that, as
$[0,1)^I$
for some finite set I. Then there exists a constant C such that, as
![]() $N \to \infty $
, we have
$N \to \infty $
, we have
Above, the implicit constant depends only on
![]() $g_{\bullet }$
.
$g_{\bullet }$
.
Our next goal is to obtain a similar bound for the number of prefixes of a bounded GP map parametrized by
![]() $\mathbb {R}^I$
. Even though we are ultimately interested in bounded GP maps, Proposition 3.4 concerning unbounded GP maps is more amenable to proof by structural induction. We will use the following induction scheme.
$\mathbb {R}^I$
. Even though we are ultimately interested in bounded GP maps, Proposition 3.4 concerning unbounded GP maps is more amenable to proof by structural induction. We will use the following induction scheme.
Proposition 3.3. [Reference Adamczewski and KoniecznyAK23, Proposition 13.9]
Let
![]() $\mathcal {G}$
be a family of parametric GP maps from
$\mathcal {G}$
be a family of parametric GP maps from
![]() $\mathbb {Z}$
to
$\mathbb {Z}$
to
![]() $\mathbb {Z}$
with index sets contained in
$\mathbb {Z}$
with index sets contained in
![]() $\mathbb {N}$
. Suppose that
$\mathbb {N}$
. Suppose that
![]() $\mathcal {G}$
has the following closure properties.
$\mathcal {G}$
has the following closure properties.
-
(i) All GP maps
 $\mathbb {Z} \to \mathbb {Z}$
belong to
$\mathbb {Z} \to \mathbb {Z}$
belong to
 $\mathcal {G}$
.
$\mathcal {G}$
. -
(ii) For every
 $g_{\bullet }$
and
$g_{\bullet }$
and
 $h_{\bullet } \in \mathcal {G}$
, we have that
$h_{\bullet } \in \mathcal {G}$
, we have that
 $g_{\bullet }+h_{\bullet } \in \mathcal {G}$
and
$g_{\bullet }+h_{\bullet } \in \mathcal {G}$
and
 $g_{\bullet } \cdot h_{\bullet } \in \mathcal {G}$
.
$g_{\bullet } \cdot h_{\bullet } \in \mathcal {G}$
. -
(iii) For every
 $g_\bullet \in \mathcal {G}$
,
$g_\bullet \in \mathcal {G}$
,
 $\mathcal {G}$
contains all the parametric GP maps
$\mathcal {G}$
contains all the parametric GP maps
 $g^\prime _\bullet \colon \mathbb {Z} \to \mathbb {Z}$
satisfying
$g^\prime _\bullet \colon \mathbb {Z} \to \mathbb {Z}$
satisfying
 $g_\bullet \succeq g^\prime _\bullet $
.
$g_\bullet \succeq g^\prime _\bullet $
. -
(iv) For every pair of disjoint finite sets
 $I \subseteq \mathbb {N}$
,
$I \subseteq \mathbb {N}$
,
 $J \subseteq \mathbb {N}$
, and every sequence of parametric GP maps
$J \subseteq \mathbb {N}$
, and every sequence of parametric GP maps
 $h^{(i)}_{\bullet } \in \mathcal {G}$
,
$h^{(i)}_{\bullet } \in \mathcal {G}$
,
 $i \in I$
, with index set J,
$i \in I$
, with index set J,
 $\mathcal {G}$
contains the parametric GP map
$\mathcal {G}$
contains the parametric GP map
 $g_\bullet $
defined by
$g_\bullet $
defined by  $$ \begin{align*} g_{\alpha,\beta}(n) = \bigg\lfloor \sum_{i\in I} \alpha_i h^{(i)}_{\beta}(n) \bigg\rfloor , \quad n \in \mathbb{Z},\ \alpha \in \mathbb{R}^{I},\ \beta \in \mathbb{R}^J.\end{align*} $$
$$ \begin{align*} g_{\alpha,\beta}(n) = \bigg\lfloor \sum_{i\in I} \alpha_i h^{(i)}_{\beta}(n) \bigg\rfloor , \quad n \in \mathbb{Z},\ \alpha \in \mathbb{R}^{I},\ \beta \in \mathbb{R}^J.\end{align*} $$
Then
![]() $\mathcal {G}$
contains all parametric GP maps
$\mathcal {G}$
contains all parametric GP maps
![]() $\mathbb {Z} \to \mathbb {Z}$
with index sets contained in
$\mathbb {Z} \to \mathbb {Z}$
with index sets contained in
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
Proposition 3.4. Let
![]() $g_{\bullet } \colon \mathbb {Z} \to \mathbb {Z}$
be a GP map parametrized by
$g_{\bullet } \colon \mathbb {Z} \to \mathbb {Z}$
be a GP map parametrized by
![]() $\mathbb {R}^I$
for a finite set I. Then there exist finite sets
$\mathbb {R}^I$
for a finite set I. Then there exist finite sets
![]() $J,K$
and a GP map
$J,K$
and a GP map
![]() $\widetilde g_\bullet \colon \mathbb {Z} \to \mathbb {Z}$
parametrized by
$\widetilde g_\bullet \colon \mathbb {Z} \to \mathbb {Z}$
parametrized by
![]() $\mathbb {Z}^J \times [0,1)^K$
such that
$\mathbb {Z}^J \times [0,1)^K$
such that
![]() $\widetilde g_\bullet \succeq g_\bullet $
and
$\widetilde g_\bullet \succeq g_\bullet $
and
![]() $\widetilde g_\bullet $
takes the form
$\widetilde g_\bullet $
takes the form
 $$ \begin{align*} \widetilde g_{a,\beta} &= \sum_{j \in J} a_j h^{(j)}_{\beta}, \quad a \in \mathbb{Z}^J,\ \beta \in [0,1)^K, \end{align*} $$
$$ \begin{align*} \widetilde g_{a,\beta} &= \sum_{j \in J} a_j h^{(j)}_{\beta}, \quad a \in \mathbb{Z}^J,\ \beta \in [0,1)^K, \end{align*} $$
where for each
![]() $j \in J$
,
$j \in J$
,
![]() $h^{(j)}_{\bullet } \colon \mathbb {Z} \to \mathbb {Z}$
is a GP map parametrized by
$h^{(j)}_{\bullet } \colon \mathbb {Z} \to \mathbb {Z}$
is a GP map parametrized by
![]() $[0,1)^K$
.
$[0,1)^K$
.
Proof. (i) If
![]() $g \colon \mathbb {Z} \to \mathbb {Z}$
is a fixed GP map (that is, if
$g \colon \mathbb {Z} \to \mathbb {Z}$
is a fixed GP map (that is, if
![]() $I = \emptyset $
) then we can simply take
$I = \emptyset $
) then we can simply take
![]() $\widetilde g = g$
.
$\widetilde g = g$
.
(ii) Suppose that the conclusion holds for
![]() $g_\bullet ,h_\bullet \colon \mathbb {Z} \to \mathbb {Z}$
, and let the corresponding extensions
$g_\bullet ,h_\bullet \colon \mathbb {Z} \to \mathbb {Z}$
, and let the corresponding extensions
![]() $\widetilde g_{\bullet }$
and
$\widetilde g_{\bullet }$
and
![]() $\widetilde h_\bullet $
be given by
$\widetilde h_\bullet $
be given by
 $$ \begin{align*} \widetilde g_{a,\beta} &= \sum_{j \in J} a_j h^{(j)}_{\beta}, \quad a \in \mathbb{Z}^J,\ \beta \in [0,1)^K, \\ \widetilde h_{c,\delta} &= \sum_{l \in L} c_{l} h^{(l)}_{\delta}, \quad c \in \mathbb{Z}^L,\ \delta \in [0,1)^M. \end{align*} $$
$$ \begin{align*} \widetilde g_{a,\beta} &= \sum_{j \in J} a_j h^{(j)}_{\beta}, \quad a \in \mathbb{Z}^J,\ \beta \in [0,1)^K, \\ \widetilde h_{c,\delta} &= \sum_{l \in L} c_{l} h^{(l)}_{\delta}, \quad c \in \mathbb{Z}^L,\ \delta \in [0,1)^M. \end{align*} $$
We may freely assume that the index sets
![]() $J,K,L,M$
are pairwise disjoint. We will show that the conclusion also holds for
$J,K,L,M$
are pairwise disjoint. We will show that the conclusion also holds for
![]() $g_{\bullet } + h_{\bullet }$
and
$g_{\bullet } + h_{\bullet }$
and
![]() $g_{\bullet } \cdot h_{\bullet }$
. In the case of
$g_{\bullet } \cdot h_{\bullet }$
. In the case of
![]() $g_{\bullet } + h_{\bullet }$
it is enough to combine the sums representing
$g_{\bullet } + h_{\bullet }$
it is enough to combine the sums representing
![]() $\widetilde g_{a,\beta } $
and
$\widetilde g_{a,\beta } $
and
![]() $\widetilde h_{c,\delta }$
into a single sum. In the case of
$\widetilde h_{c,\delta }$
into a single sum. In the case of
![]() $g_{\bullet } \cdot h_{\bullet }$
, we take
$g_{\bullet } \cdot h_{\bullet }$
, we take
 $$ \begin{align*} \widetilde f_{e,(\beta,\delta)} &= \sum_{j \in J,\ l \in L} e_{j,l} ( h^{(j)}_{\beta} \cdot h^{(l)}_{\delta} ), \quad e \in \mathbb{Z}^{J \times L},\ (\beta,\delta) \in [0,1)^{K\times M}. \end{align*} $$
$$ \begin{align*} \widetilde f_{e,(\beta,\delta)} &= \sum_{j \in J,\ l \in L} e_{j,l} ( h^{(j)}_{\beta} \cdot h^{(l)}_{\delta} ), \quad e \in \mathbb{Z}^{J \times L},\ (\beta,\delta) \in [0,1)^{K\times M}. \end{align*} $$
Then
![]() $\widetilde f$
has the required form and (taking
$\widetilde f$
has the required form and (taking
![]() $e_{j,l} = a_j c_l$
) we see that
$e_{j,l} = a_j c_l$
) we see that
![]() $\widetilde f_{\bullet } \succeq \widetilde g_{\bullet } \cdot \widetilde h_{\bullet } \succeq g_{\bullet } \cdot h_{\bullet }$
.
$\widetilde f_{\bullet } \succeq \widetilde g_{\bullet } \cdot \widetilde h_{\bullet } \succeq g_{\bullet } \cdot h_{\bullet }$
.
(iii) Suppose that the conclusion holds for
![]() $g_\bullet $
and that
$g_\bullet $
and that
![]() $g_{\bullet } \succeq g^\prime _\bullet $
. Then the conclusion also holds for
$g_{\bullet } \succeq g^\prime _\bullet $
. Then the conclusion also holds for
![]() $g^\prime _{\bullet }$
because the relation of being an extension is transitive.
$g^\prime _{\bullet }$
because the relation of being an extension is transitive.
(iv) Suppose that
![]() $I \subseteq \mathbb {N}$
,
$I \subseteq \mathbb {N}$
,
![]() $J \subseteq \mathbb {N}$
are disjoint finite sets,
$J \subseteq \mathbb {N}$
are disjoint finite sets,
![]() $h^{(i)}_{\bullet }$
are GP maps parametrized by
$h^{(i)}_{\bullet }$
are GP maps parametrized by
![]() $\mathbb {R}^J$
which satisfy the conclusion for each for
$\mathbb {R}^J$
which satisfy the conclusion for each for
![]() $i \in I$
, and
$i \in I$
, and
![]() $g_\bullet $
is the parametric GP map defined by
$g_\bullet $
is the parametric GP map defined by
 $$ \begin{align*} g_{\alpha,\beta}(n) &:= \bigg\lfloor \sum_{i\in I} \alpha_i h^{(i)}_{\beta}(n) \bigg\rfloor ,\quad n \in \mathbb{Z},\ \alpha \in \mathbb{R}^{I},\ \beta \in \mathbb{R}^J. \end{align*} $$
$$ \begin{align*} g_{\alpha,\beta}(n) &:= \bigg\lfloor \sum_{i\in I} \alpha_i h^{(i)}_{\beta}(n) \bigg\rfloor ,\quad n \in \mathbb{Z},\ \alpha \in \mathbb{R}^{I},\ \beta \in \mathbb{R}^J. \end{align*} $$
Let the extensions of
![]() $h^{(i)}$
be given by
$h^{(i)}$
be given by
(Note that without loss of generality we may use the same index sets L and M for each
![]() $i \in I$
.) We will show that the conclusion is satisfied for
$i \in I$
.) We will show that the conclusion is satisfied for
![]() $g_\bullet $
. We observe that we have the equality
$g_\bullet $
. We observe that we have the equality
 $$ \begin{align*} \bigg\lfloor \sum_{i\in I} \alpha_i \widetilde h_{c,\delta}^{(i)} \bigg\rfloor &= \bigg\lfloor \sum_{i\in I,\ l \in L} \kern-2pt\alpha_i c_{l} f^{(i,l)}_{\delta} \!\bigg\rfloor = \sum_{i\in I,\ l \in L} \kern-1pt\lfloor \alpha_i c_{l} \rfloor f^{(i,l)}_{\delta} + \bigg\lfloor \sum_{i\in I,\ l \in L} \kern-1pt\{ \alpha_i c_{l} \} f^{(i,l)}_{\delta} \!\bigg\rfloor. \end{align*} $$
$$ \begin{align*} \bigg\lfloor \sum_{i\in I} \alpha_i \widetilde h_{c,\delta}^{(i)} \bigg\rfloor &= \bigg\lfloor \sum_{i\in I,\ l \in L} \kern-2pt\alpha_i c_{l} f^{(i,l)}_{\delta} \!\bigg\rfloor = \sum_{i\in I,\ l \in L} \kern-1pt\lfloor \alpha_i c_{l} \rfloor f^{(i,l)}_{\delta} + \bigg\lfloor \sum_{i\in I,\ l \in L} \kern-1pt\{ \alpha_i c_{l} \} f^{(i,l)}_{\delta} \!\bigg\rfloor. \end{align*} $$
This motivates us to define
 $$ \begin{align*} \widetilde g_{e,\delta,\phi} &:= \sum_{i \in I,\ l \in L} e_{i,l} f^{(i,l)}_{\delta} + e_{\diamond} \bigg\lfloor \sum_{i\in I,\ l \in L} \phi_{i,l} f^{(i,l)}_{\delta} \bigg\rfloor, \\ & e \in \mathbb{Z}^{I \times L \cup \{\diamond\}}, \phi \in [0,1)^{I \times L}, \delta \in [0,1)^M, \end{align*} $$
$$ \begin{align*} \widetilde g_{e,\delta,\phi} &:= \sum_{i \in I,\ l \in L} e_{i,l} f^{(i,l)}_{\delta} + e_{\diamond} \bigg\lfloor \sum_{i\in I,\ l \in L} \phi_{i,l} f^{(i,l)}_{\delta} \bigg\rfloor, \\ & e \in \mathbb{Z}^{I \times L \cup \{\diamond\}}, \phi \in [0,1)^{I \times L}, \delta \in [0,1)^M, \end{align*} $$
where
![]() $\diamond $
is some index that does not belong to
$\diamond $
is some index that does not belong to
![]() $I \times J$
. Letting also
$I \times J$
. Letting also
 $$ \begin{align*} f^{(\diamond)}_{\delta,\phi} := \bigg\lfloor \sum_{i\in I,\ l \in L} \phi_{i,l} f^{(i,l)}_{\delta} \bigg\rfloor,\quad \phi \in [0,1)^{I \times L},\ \delta \in [0,1)^M, \end{align*} $$
$$ \begin{align*} f^{(\diamond)}_{\delta,\phi} := \bigg\lfloor \sum_{i\in I,\ l \in L} \phi_{i,l} f^{(i,l)}_{\delta} \bigg\rfloor,\quad \phi \in [0,1)^{I \times L},\ \delta \in [0,1)^M, \end{align*} $$
we see that
![]() $\widetilde g_{\bullet }$
takes the required form and (setting
$\widetilde g_{\bullet }$
takes the required form and (setting
![]() $\phi _{i,l} = \{ \alpha _i c_l \} $
and
$\phi _{i,l} = \{ \alpha _i c_l \} $
and
![]() $e_{\diamond } = 1$
) we have
$e_{\diamond } = 1$
) we have
![]() $\widetilde g_\bullet \succeq g_\bullet $
.
$\widetilde g_\bullet \succeq g_\bullet $
.
Combining the closure properties proved above, we infer from Proposition 3.3 that the conclusion holds for all parametric GP maps.
Proposition 3.5. Let
![]() $M \in \mathbb {N}$
and let
$M \in \mathbb {N}$
and let
![]() $g_{\bullet } \colon \mathbb {Z} \to [M]$
be a GP map parametrized by
$g_{\bullet } \colon \mathbb {Z} \to [M]$
be a GP map parametrized by
![]() $\mathbb {R}^I$
for a finite set I. Then there exists a GP map
$\mathbb {R}^I$
for a finite set I. Then there exists a GP map
![]() $\widetilde g_\bullet \colon \mathbb {Z} \to [M]$
parametrized by
$\widetilde g_\bullet \colon \mathbb {Z} \to [M]$
parametrized by
![]() $[0,1)^J$
for a finite set J such that
$[0,1)^J$
for a finite set J such that
![]() $\widetilde g_\bullet \succeq g_\bullet $
.
$\widetilde g_\bullet \succeq g_\bullet $
.
Proof. Let
![]() $\widetilde g^{(0)}_{\bullet } \succeq g_{\bullet }$
be the parametric GP from Proposition 3.4, and let
$\widetilde g^{(0)}_{\bullet } \succeq g_{\bullet }$
be the parametric GP from Proposition 3.4, and let
 $$ \begin{align*} \widetilde g_{a,\beta}^{(0)} &= \sum_{j \in J} a_j h^{(j)}_{\beta}, \quad a \in \mathbb{Z}^J, \beta \in [0,1)^K. \end{align*} $$
$$ \begin{align*} \widetilde g_{a,\beta}^{(0)} &= \sum_{j \in J} a_j h^{(j)}_{\beta}, \quad a \in \mathbb{Z}^J, \beta \in [0,1)^K. \end{align*} $$
Since the value of
![]() $g_{\alpha ,\beta }(n)$
is completely determined by its residue modulo M, we expect that it is enough to consider the values of a with
$g_{\alpha ,\beta }(n)$
is completely determined by its residue modulo M, we expect that it is enough to consider the values of a with
![]() $a \in [M]^J$
. This motivates us to put
$a \in [M]^J$
. This motivates us to put
 $$ \begin{align*} \widetilde g_{\alpha,\beta} &= \sum_{j \in J} \lfloor M \alpha_j \rfloor h^{(j)}_{\beta}, \quad \alpha \in [0,1)^J, \beta \in [0,1)^K. \end{align*} $$
$$ \begin{align*} \widetilde g_{\alpha,\beta} &= \sum_{j \in J} \lfloor M \alpha_j \rfloor h^{(j)}_{\beta}, \quad \alpha \in [0,1)^J, \beta \in [0,1)^K. \end{align*} $$
Let
![]() $\phi \colon \mathbb {Z}^I \to \mathbb {Z}^J$
and
$\phi \colon \mathbb {Z}^I \to \mathbb {Z}^J$
and
![]() $\psi \colon \mathbb {Z}^I \to \mathbb {R}^K$
be GP maps such that
$\psi \colon \mathbb {Z}^I \to \mathbb {R}^K$
be GP maps such that
![]() $g_{\alpha } = \widetilde g^{(0)}_{\phi (\alpha ),\psi (\alpha )}$
. Let
$g_{\alpha } = \widetilde g^{(0)}_{\phi (\alpha ),\psi (\alpha )}$
. Let
![]() $\theta \colon \mathbb {Z}^I \to [0,1)^J$
be given by
$\theta \colon \mathbb {Z}^I \to [0,1)^J$
be given by
![]() $\theta (\alpha ) := \{ \phi (\alpha )/M \} $
(with fractional part taken coordinatewise). Then
$\theta (\alpha ) := \{ \phi (\alpha )/M \} $
(with fractional part taken coordinatewise). Then
Since
![]() $g_{\bullet }$
takes values in
$g_{\bullet }$
takes values in
![]() $[M]$
, it follows that
$[M]$
, it follows that
Replacing
![]() $\widetilde g_\bullet $
with
$\widetilde g_\bullet $
with
![]() $M \cdot \{ \widetilde {g_\bullet }/M \} $
if necessary, we may further ensure that
$M \cdot \{ \widetilde {g_\bullet }/M \} $
if necessary, we may further ensure that
![]() $\widetilde g_\bullet $
takes values in
$\widetilde g_\bullet $
takes values in
![]() $[M]$
. As a consequence,
$[M]$
. As a consequence,
![]() $\widetilde g_\bullet \succeq g_\bullet $
, as needed.
$\widetilde g_\bullet \succeq g_\bullet $
, as needed.
Proposition 3.6. Let
![]() $\mathbf a = (a(n))_{n \in \mathbb {Z}}$
be a (two-sided) bracket word over a finite alphabet
$\mathbf a = (a(n))_{n \in \mathbb {Z}}$
be a (two-sided) bracket word over a finite alphabet
![]() $\Sigma $
, and let
$\Sigma $
, and let
![]() $g_{\bullet } \colon \mathbb {Z} \to \mathbb {Z}$
be a GP map parametrized by
$g_{\bullet } \colon \mathbb {Z} \to \mathbb {Z}$
be a GP map parametrized by
![]() $\mathbb {R}^I$
for some finite set I. Then there exists a constant
$\mathbb {R}^I$
for some finite set I. Then there exists a constant
![]() $C> 0$
such that, as
$C> 0$
such that, as
![]() $N \to \infty $
, we have
$N \to \infty $
, we have
Above, the implicit constant depends on
![]() $\mathbf a$
and
$\mathbf a$
and
![]() $g_\bullet $
.
$g_\bullet $
.
Proof. Let
![]() $M := |\Sigma |$
. We may freely assume that
$M := |\Sigma |$
. We may freely assume that
![]() $\Sigma = [M]$
, in which case a is a GP map by [Reference Adamczewski and KoniecznyAK23, Lemma 5.2]. Thus,
$\Sigma = [M]$
, in which case a is a GP map by [Reference Adamczewski and KoniecznyAK23, Lemma 5.2]. Thus,
![]() $a\circ g_{\bullet }$
is a GP map parametrized by
$a\circ g_{\bullet }$
is a GP map parametrized by
![]() $\mathbb {R}^I$
and taking values in
$\mathbb {R}^I$
and taking values in
![]() $[M]$
. By Proposition 3.5, there exists a GP map
$[M]$
. By Proposition 3.5, there exists a GP map
![]() $\widetilde g_{\bullet }$
parametrized by
$\widetilde g_{\bullet }$
parametrized by
![]() $[0,1)^J$
for a finite set J such that
$[0,1)^J$
for a finite set J such that
![]() $\widetilde g_{\bullet } \succeq a \circ g_{\bullet }$
. Thus, it suffices to show that, for a certain
$\widetilde g_{\bullet } \succeq a \circ g_{\bullet }$
. Thus, it suffices to show that, for a certain
![]() $C> 0$
, the number of words
$C> 0$
, the number of words
![]() $ ( \widetilde g_{\alpha }(n) )_{n=0}^{N-1}$
for
$ ( \widetilde g_{\alpha }(n) )_{n=0}^{N-1}$
for
![]() $\alpha \in [0,1)^J$
is
$\alpha \in [0,1)^J$
is
![]() $O(N^C)$
as
$O(N^C)$
as
![]() $N \to \infty $
. This is precisely Theorem 3.2.
$N \to \infty $
. This is precisely Theorem 3.2.
As a special case, we obtain a bound on the number of subsequences of bracket words along polynomials of a given degree.
Corollary 3.7. Let
![]() $\mathbf a = (a(n))_{n \in \mathbb {Z}}$
be a (two-sided) bracket word over a finite alphabet
$\mathbf a = (a(n))_{n \in \mathbb {Z}}$
be a (two-sided) bracket word over a finite alphabet
![]() $\Sigma $
and let
$\Sigma $
and let
![]() $d \in \mathbb {N}$
. Then there exists a constant
$d \in \mathbb {N}$
. Then there exists a constant
![]() $C> 0$
such that, as
$C> 0$
such that, as
![]() $N\to \infty $
, we have
$N\to \infty $
, we have
where the implied constant depends only on
![]() $\mathbf a$
and d.
$\mathbf a$
and d.
Thus we are now in a position to prove Theorem A.
Proof of Theorem A
We aim to estimate the number of subwords of length H of
![]() $(a(\lfloor f(n) \rfloor ))_{n=0}^{\infty }$
, that is, we count words of the form
$(a(\lfloor f(n) \rfloor ))_{n=0}^{\infty }$
, that is, we count words of the form
for
![]() $N\in \mathbb {N}$
. Since f has polynomial growth, there exists
$N\in \mathbb {N}$
. Since f has polynomial growth, there exists
![]() $k \in \mathbb {N}$
such that
$k \in \mathbb {N}$
such that
![]() $f(t) \ll t^k$
. We choose
$f(t) \ll t^k$
. We choose
![]() $\ell \geq k+1$
and apply Theorem 2.11 to find some
$\ell \geq k+1$
and apply Theorem 2.11 to find some
![]() $0<\eta <1$
such that for any
$0<\eta <1$
such that for any
![]() $H \in \mathbb {N}$
at least one of statements (i)–(iii) in Theorem 2.11 holds, where
$H \in \mathbb {N}$
at least one of statements (i)–(iii) in Theorem 2.11 holds, where
and
![]() $P_{N,\ell }$
is the Taylor polynomial of f (see (4)). We distinguish the three possible cases. Obviously (i) contributes at most
$P_{N,\ell }$
is the Taylor polynomial of f (see (4)). We distinguish the three possible cases. Obviously (i) contributes at most
![]() $O(H^{\ell + 1})$
different words. For (ii) we first consider
$O(H^{\ell + 1})$
different words. For (ii) we first consider
![]() $a(\lfloor P_{N,\ell }(h) \rfloor )_{h=0}^{H-1}$
. By Corollary 3.7 this word is contained in a set of size
$a(\lfloor P_{N,\ell }(h) \rfloor )_{h=0}^{H-1}$
. By Corollary 3.7 this word is contained in a set of size
![]() $O(H^C)$
. By assumption
$O(H^C)$
. By assumption
![]() $a(\lfloor f(N+h) \rfloor ) \neq a(\lfloor P_{N,\ell }(h) \rfloor )$
for at most
$a(\lfloor f(N+h) \rfloor ) \neq a(\lfloor P_{N,\ell }(h) \rfloor )$
for at most
![]() $O(H^{\eta })$
values of
$O(H^{\eta })$
values of
![]() $h\in [H]$
, which can be chosen in
$h\in [H]$
, which can be chosen in
![]() $\binom {H}{O(H^{\eta })}$
ways For each position h with
$\binom {H}{O(H^{\eta })}$
ways For each position h with
![]() $a(\lfloor f(N+h) \rfloor ) \neq a(\lfloor P_{N,\ell }(h) \rfloor )$
we have at most
$a(\lfloor f(N+h) \rfloor ) \neq a(\lfloor P_{N,\ell }(h) \rfloor )$
we have at most
![]() $|\Sigma |$
possibilities for the value of
$|\Sigma |$
possibilities for the value of
![]() $a(\lfloor f(N+h) \rfloor )$
. In total, we can estimate the number of subwords of length H in this case (up to a constant) by
$a(\lfloor f(N+h) \rfloor )$
. In total, we can estimate the number of subwords of length H in this case (up to a constant) by
 $$ \begin{align*} H^C \cdot \binom{H}{O(H^{\eta})} \cdot |\Sigma|^{O(H^{\eta})} &\leq H^C \cdot H^{O(H^{\eta})} \cdot |\Sigma|^{O(H^{\eta})}\\ &= \exp( C \log H + O((\log H) \cdot H^{\eta}) + O((\log |\Sigma|) \cdot H^{\eta}) )\\ &= \exp( O_{C, \eta}(H^{(1+\eta)/2}) ). \end{align*} $$
$$ \begin{align*} H^C \cdot \binom{H}{O(H^{\eta})} \cdot |\Sigma|^{O(H^{\eta})} &\leq H^C \cdot H^{O(H^{\eta})} \cdot |\Sigma|^{O(H^{\eta})}\\ &= \exp( C \log H + O((\log H) \cdot H^{\eta}) + O((\log |\Sigma|) \cdot H^{\eta}) )\\ &= \exp( O_{C, \eta}(H^{(1+\eta)/2}) ). \end{align*} $$
In the last case (iii) we decompose
![]() $[H]$
into
$[H]$
into
![]() $O(H^{\eta })$
arithmetic progressions on which
$O(H^{\eta })$
arithmetic progressions on which
![]() $e_N$
is constant. We let these arithmetic progressions be denoted by
$e_N$
is constant. We let these arithmetic progressions be denoted by
![]() $P_1, \ldots , P_s$
. As there are at most
$P_1, \ldots , P_s$
. As there are at most
![]() $H^3$
arithmetic progressions contained in
$H^3$
arithmetic progressions contained in
![]() $[H]$
we can bound the number of possible different decompositions by
$[H]$
we can bound the number of possible different decompositions by
![]() $(H^3)^{O(H^{\eta })}$
. On every such progression there exists a polynomial q (which is either
$(H^3)^{O(H^{\eta })}$
. On every such progression there exists a polynomial q (which is either
![]() $P_{N,\ell }, P_{N,\ell }+1$
or
$P_{N,\ell }, P_{N,\ell }+1$
or
![]() $P_{N,\ell }-1$
) such that
$P_{N,\ell }-1$
) such that
![]() $a(\lfloor f(N+h) \rfloor ) = a(\lfloor q(h) \rfloor )$
. As a polynomial along an arithmetic progression is again a polynomial, by Corollary 3.7 we can bound the number of subwords appearing along some
$a(\lfloor f(N+h) \rfloor ) = a(\lfloor q(h) \rfloor )$
. As a polynomial along an arithmetic progression is again a polynomial, by Corollary 3.7 we can bound the number of subwords appearing along some
![]() $P_j$
by
$P_j$
by
![]() $H^C$
. In total, we can estimate the number of subwords of length H in this case by
$H^C$
. In total, we can estimate the number of subwords of length H in this case by
 $$ \begin{align*} (H^3)^{O(H^{\eta})}\cdot (H^C)^{O(H^{\eta})} &= \exp( (C+3) \log(H) \cdot O(H^{\eta}))\\ &= \exp(O_{C,\eta}(H^{(1+\eta)/2})). \end{align*} $$
$$ \begin{align*} (H^3)^{O(H^{\eta})}\cdot (H^C)^{O(H^{\eta})} &= \exp( (C+3) \log(H) \cdot O(H^{\eta}))\\ &= \exp(O_{C,\eta}(H^{(1+\eta)/2})). \end{align*} $$
This finishes the proof for
![]() $\delta = (1+\eta )/2 < 1$
.
$\delta = (1+\eta )/2 < 1$
.
4 Nilmanifolds
In this section we recall some basic definitions and results on nilmanifolds and discuss the connection to generalized polynomials which goes back to the work of Bergelson and Leibman [Reference Bergelson and LeibmanBL07].
4.1 Basic definitions
In this section we very briefly introduce definitions and basic facts related to nilmanifolds and nilpotent dynamics. Throughout this section, we let G denote an s-step nilpotent Lie group of some dimension D. We assume that G is connected and simply connected. We also let
![]() $\Gamma < G$
denote a subgroup that is discrete and cocompact, meaning that the quotient space
$\Gamma < G$
denote a subgroup that is discrete and cocompact, meaning that the quotient space
![]() $G/\Gamma $
is compact. The space
$G/\Gamma $
is compact. The space
![]() $X = G/\Gamma $
is called an s-step nilmanifold. A degree- d filtration on G is a sequence
$X = G/\Gamma $
is called an s-step nilmanifold. A degree- d filtration on G is a sequence
![]() $G_\bullet $
of subgroups
$G_\bullet $
of subgroups
such that
![]() $G_{d+1} = \{e_G\}$
(and hence
$G_{d+1} = \{e_G\}$
(and hence
![]() $G_{i} = \{e_G\}$
for all
$G_{i} = \{e_G\}$
for all
![]() $i> d$
) and for each
$i> d$
) and for each
![]() $i,j$
we have
$i,j$
we have
![]() $[G_i,G_j] \subseteq G_{i+j}$
, where
$[G_i,G_j] \subseteq G_{i+j}$
, where
![]() $[G_i,G_j]$
is the group generated by the commutators
$[G_i,G_j]$
is the group generated by the commutators
![]() $[g,h] = ghg^{-1}h^{-1}$
with
$[g,h] = ghg^{-1}h^{-1}$
with
![]() $g \in G_i$
,
$g \in G_i$
,
![]() $h \in G_j$
. A standard example of a filtration is the lower central series given by
$h \in G_j$
. A standard example of a filtration is the lower central series given by
![]() $G_{(0)} = G_{(1)} = G$
and
$G_{(0)} = G_{(1)} = G$
and
![]() $G_{(i+1)} = [G,G_{(i)}]$
for
$G_{(i+1)} = [G,G_{(i)}]$
for
![]() $i \geq 1$
.
$i \geq 1$
.
A Mal’cev basis compatible with
![]() $\Gamma $
and
$\Gamma $
and
![]() $G_\bullet $
is a basis
$G_\bullet $
is a basis ![]() of the Lie algebra
of the Lie algebra
![]() $\mathfrak {g}$
of G such that:
$\mathfrak {g}$
of G such that:
-
(i) for each
 $0 \leq j \leq D$
, the subspace
$0 \leq j \leq D$
, the subspace
 $\mathfrak {h}_j := \operatorname {span}( X_{j+1},X_{j+2},\dots ,X_D )$
is a Lie algebra ideal in
$\mathfrak {h}_j := \operatorname {span}( X_{j+1},X_{j+2},\dots ,X_D )$
is a Lie algebra ideal in
 $\mathfrak {g}$
;
$\mathfrak {g}$
; -
(ii) for each
 $0 \leq i \leq d$
, each
$0 \leq i \leq d$
, each
 $g \in G_i$
has a unique representation as
$g \in G_i$
has a unique representation as
 $g = \exp (t_{D(i) + 1} X_{t_{D(i) + 1}}) \cdots \exp (t_{D-1} X_{D-1}) \exp (t_D X_D) $
, where
$g = \exp (t_{D(i) + 1} X_{t_{D(i) + 1}}) \cdots \exp (t_{D-1} X_{D-1}) \exp (t_D X_D) $
, where
 $D(i) := \operatorname {codim} G_i$
and
$D(i) := \operatorname {codim} G_i$
and
 $t_j \in \mathbb {R}$
for
$t_j \in \mathbb {R}$
for
 $D(i) < j \leq D$
;
$D(i) < j \leq D$
; -
(iii)
 $\Gamma $
is the set of all products
$\Gamma $
is the set of all products
 $\exp (t_1 X_1) \exp (t_2 X_2) \cdots \exp (t_D X_D)$
with
$\exp (t_1 X_1) \exp (t_2 X_2) \cdots \exp (t_D X_D)$
with
 $t_j \in \mathbb {Z}$
for
$t_j \in \mathbb {Z}$
for
 $1 \leq j \leq D$
.
$1 \leq j \leq D$
.
If the Lie bracket is given in coordinates by
 $$ \begin{align*} [X_i,X_j] = \sum_{k=1}^D c^{(k)}_{i,j} X_k, \end{align*} $$
$$ \begin{align*} [X_i,X_j] = \sum_{k=1}^D c^{(k)}_{i,j} X_k, \end{align*} $$
where all of the constants
![]() $c^{(k)}_{i,j}$
are rationals with height at most M, then we will say that the complexity of
$c^{(k)}_{i,j}$
are rationals with height at most M, then we will say that the complexity of
![]() $(G,\Gamma ,G_\bullet )$
is at most M. We recall that the height of a rational number
$(G,\Gamma ,G_\bullet )$
is at most M. We recall that the height of a rational number
![]() $a/b$
is
$a/b$
is
![]() $\max (|a|,|b|)$
(
$\max (|a|,|b|)$
(
![]() $a \in \mathbb {Z}$
,
$a \in \mathbb {Z}$
,
![]() $b \in \mathbb {N}$
,
$b \in \mathbb {N}$
,
![]() $\gcd (a,b) = 1$
).
$\gcd (a,b) = 1$
).
We will usually keep the choice of the Mal’cev basis implicit, and assume that each filtered nilmanifold under consideration comes equipped with a fixed choice of Mal’cev basis. The Mal’cev basis ![]() induces bijective coordinate maps
induces bijective coordinate maps
![]() $\tau \colon X \to [0,1)^D$
and
$\tau \colon X \to [0,1)^D$
and
![]() $\widetilde \tau \colon G \to \mathbb {R}^D$
, such that
$\widetilde \tau \colon G \to \mathbb {R}^D$
, such that
 $$ \begin{align*} x &= \exp(\tau_1(x)X_1) \exp(\tau_2(x)X_2) \cdots \exp(\tau_D(x)X_D) \Gamma, \quad x \in X, \\ g &= \exp(\widetilde\tau_1(g)X_1) \exp(\widetilde\tau_2(g)X_2) \cdots \exp(\widetilde\tau_D(g)X_D), \quad g \in G. \end{align*} $$
$$ \begin{align*} x &= \exp(\tau_1(x)X_1) \exp(\tau_2(x)X_2) \cdots \exp(\tau_D(x)X_D) \Gamma, \quad x \in X, \\ g &= \exp(\widetilde\tau_1(g)X_1) \exp(\widetilde\tau_2(g)X_2) \cdots \exp(\widetilde\tau_D(g)X_D), \quad g \in G. \end{align*} $$
The Mal’cev basis also induces a natural choice of a right-invariant metric on G and a metric on X. We refer to [Reference Green and TaoGT12b, Definition 2.2] for a precise definition. Keeping the dependence on ![]() implicit, we will use the symbol d to denote either of those metrics.
implicit, we will use the symbol d to denote either of those metrics.
The space X comes equipped with the Haar measure
![]() $\mu _X$
, which is the unique Borel probability measure on X invariant under the action of G:
$\mu _X$
, which is the unique Borel probability measure on X invariant under the action of G:
![]() $\mu _X(gE) = \mu _X(E)$
for all measurable
$\mu _X(gE) = \mu _X(E)$
for all measurable
![]() $E \subseteq X$
and
$E \subseteq X$
and
![]() $g \in G$
. When there is no risk of confusion, we write
$g \in G$
. When there is no risk of confusion, we write
![]() $dx$
as a shorthand for
$dx$
as a shorthand for
![]() $d\mu _X(x)$
.
$d\mu _X(x)$
.
A map
![]() $g \colon \mathbb {Z} \to G$
is polynomial with respect to the filtration
$g \colon \mathbb {Z} \to G$
is polynomial with respect to the filtration
![]() $G_\bullet $
, denoted
$G_\bullet $
, denoted
![]() ${g \in \mathrm {poly}(\mathbb {Z},G_\bullet )}$
, if it takes the form
${g \in \mathrm {poly}(\mathbb {Z},G_\bullet )}$
, if it takes the form
where
![]() $g_i \in G_i$
for all
$g_i \in G_i$
for all
![]() $0 \leq i \leq d$
(cf. [Reference Green and TaoGT12b, Lemma 6.7]; see also [Reference Green and TaoGT12b, Definition 1.8] for an alternative definition). Although it is not immediately apparent from the definition above, polynomial sequences with respect to a given filtration form a group and are preserved under passing to an arithmetic progression (that is, if
$0 \leq i \leq d$
(cf. [Reference Green and TaoGT12b, Lemma 6.7]; see also [Reference Green and TaoGT12b, Definition 1.8] for an alternative definition). Although it is not immediately apparent from the definition above, polynomial sequences with respect to a given filtration form a group and are preserved under passing to an arithmetic progression (that is, if
![]() $g \in \mathrm {poly}(\mathbb {Z},G_\bullet )$
and
$g \in \mathrm {poly}(\mathbb {Z},G_\bullet )$
and
![]() $g'(n) := g(An+B)$
for some
$g'(n) := g(An+B)$
for some
![]() $A,B \in \mathbb {Z}$
then
$A,B \in \mathbb {Z}$
then
![]() $g' \in \mathrm {poly}(\mathbb {Z},G_\bullet )$
).
$g' \in \mathrm {poly}(\mathbb {Z},G_\bullet )$
).
4.2 Semialgebraic geometry
A basic semialgebraic set
![]() $S \subseteq \mathbb {R}^D$
is a set given by a finite number of polynomial equalities and inequalities:
$S \subseteq \mathbb {R}^D$
is a set given by a finite number of polynomial equalities and inequalities:
A semialgebraic set is a finite union of basic semialgebraic sets. In a somewhat ad hoc manner, we define the complexity of the basic semialgebraic set S given by (11) to be the sum
![]() $\sum _{i=1}^n \deg P_i + \sum _{j=1}^m \deg Q_j$
of degrees of polynomials appearing in its definition. (Strictly speaking, we take the infimum over all representations of S in the form (11).) We also define the complexity of a semialgebraic set
$\sum _{i=1}^n \deg P_i + \sum _{j=1}^m \deg Q_j$
of degrees of polynomials appearing in its definition. (Strictly speaking, we take the infimum over all representations of S in the form (11).) We also define the complexity of a semialgebraic set
represented to be the finite union of basic semialgebraic sets
![]() $S_i$
as the sum of complexities of
$S_i$
as the sum of complexities of
![]() $S_i$
. (Again, we take the infimum over all representations (12).)
$S_i$
. (Again, we take the infimum over all representations (12).)
Using the Mal’cev coordinates to identify the nilmanifold X with
![]() $[0,1)^D$
, we extend the notion of a semialgebraic set to subsets of X. A map
$[0,1)^D$
, we extend the notion of a semialgebraic set to subsets of X. A map
![]() $F \colon X \to \mathbb {R}$
is piecewise polynomial if there exists a partition
$F \colon X \to \mathbb {R}$
is piecewise polynomial if there exists a partition
![]() $X = \bigcup _{i=1}^r S_i$
into semialgebraic pieces and polynomial maps
$X = \bigcup _{i=1}^r S_i$
into semialgebraic pieces and polynomial maps
![]() $\Phi _i \colon \mathbb {R}^D \to \mathbb {R}$
such that
$\Phi _i \colon \mathbb {R}^D \to \mathbb {R}$
such that
![]() $F(x) = \Phi _i(\tau (x))$
for each
$F(x) = \Phi _i(\tau (x))$
for each
![]() $1 \leq i \leq r$
and
$1 \leq i \leq r$
and
![]() $x \in S_i$
. One can check that these notions are independent of the choice of basis, although strictly speaking we will not need this fact.
$x \in S_i$
. One can check that these notions are independent of the choice of basis, although strictly speaking we will not need this fact.
4.3 Quantitative equidistribution
The Lipschitz norm of a function
![]() $F \colon X \to \mathbb {R}$
is defined as
$F \colon X \to \mathbb {R}$
is defined as
 $$ \begin{align*} \lVert F \rVert_{\mathrm{Lip}} = \lVert F \rVert_{\infty} + \sup_{x,y \in X,\ x \neq y} \frac{|F(x)-F(y)|}{d(x,y)}. \end{align*} $$
$$ \begin{align*} \lVert F \rVert_{\mathrm{Lip}} = \lVert F \rVert_{\infty} + \sup_{x,y \in X,\ x \neq y} \frac{|F(x)-F(y)|}{d(x,y)}. \end{align*} $$
A sequence
![]() $(x_n)_{n=0}^{N-1}$
in X is
$(x_n)_{n=0}^{N-1}$
in X is
![]() $\delta $
-equidistributed if for each Lipschitz function
$\delta $
-equidistributed if for each Lipschitz function
![]() $F \colon X \to \mathbb {R}$
we have
$F \colon X \to \mathbb {R}$
we have

In the case where
![]() $X = [0,1]$
this notion is highly connected to the discrepancy of a sequence (see (2)). In fact, for
$X = [0,1]$
this notion is highly connected to the discrepancy of a sequence (see (2)). In fact, for
![]() $\delta>0$
small enough we have that
$\delta>0$
small enough we have that
![]() $(x_n)_{n=0}^{N-1}$
has discrepancy
$(x_n)_{n=0}^{N-1}$
has discrepancy
![]() $\delta $
if and only if it is
$\delta $
if and only if it is
![]() $\delta ^{O(1)}$
distributed. One direction follows immediately from the Koksma–Hlawka inequality and the other direction can be found for example in the proof of [Reference Deshouillers, Drmota, Müllner, Shubin and SpiegelhoferDDM+22, Proposition 5.2].
$\delta ^{O(1)}$
distributed. One direction follows immediately from the Koksma–Hlawka inequality and the other direction can be found for example in the proof of [Reference Deshouillers, Drmota, Müllner, Shubin and SpiegelhoferDDM+22, Proposition 5.2].
More restrictively,
![]() $(x_n)_{n=0}^{N-1}$
is totally
$(x_n)_{n=0}^{N-1}$
is totally
![]() $\delta $
-equidistributed if for each arithmetic progression
$\delta $
-equidistributed if for each arithmetic progression
![]() $P \subseteq [N]$
of length at least
$P \subseteq [N]$
of length at least
![]() $\delta N$
we have
$\delta N$
we have

A sequence
![]() $(\varepsilon _n)_{n=0}^{N-1}$
in G is
$(\varepsilon _n)_{n=0}^{N-1}$
in G is
![]() $(M,N)$
-smooth if
$(M,N)$
-smooth if
![]() $d(\varepsilon _n, e_G) \leq M$
and
$d(\varepsilon _n, e_G) \leq M$
and
![]() $d(\varepsilon _n,\varepsilon _{n+1}) \leq M/N$
for all
$d(\varepsilon _n,\varepsilon _{n+1}) \leq M/N$
for all
![]() $n \in [N-1]$
. A group element
$n \in [N-1]$
. A group element
![]() $\gamma \in G$
is Q-rational if
$\gamma \in G$
is Q-rational if
![]() $\gamma ^r \in \Gamma $
for some positive integer
$\gamma ^r \in \Gamma $
for some positive integer
![]() $r \leq Q$
. A point
$r \leq Q$
. A point
![]() $x \in G/\Gamma $
is Q-rational if it takes the form
$x \in G/\Gamma $
is Q-rational if it takes the form
![]() $x = \gamma \Gamma $
for some Q-rational
$x = \gamma \Gamma $
for some Q-rational
![]() $\gamma \in G$
. A sequence
$\gamma \in G$
. A sequence
![]() $(x_n)_{n=0}^{N-1}$
in X is Q-rational if each point
$(x_n)_{n=0}^{N-1}$
in X is Q-rational if each point
![]() $x_n$
is Q-rational.
$x_n$
is Q-rational.
Theorem 4.1. [Reference Green and TaoGT12b, Theorem 1.19]
Let
![]() $C> 0$
be a constant. Let G be a connected, simply connected nilpotent Lie group of dimension D, let
$C> 0$
be a constant. Let G be a connected, simply connected nilpotent Lie group of dimension D, let
![]() $\Gamma < G$
be a lattice, let
$\Gamma < G$
be a lattice, let
![]() $G_\bullet $
be a nilpotent filtration on G of length d, and assume that the complexity of
$G_\bullet $
be a nilpotent filtration on G of length d, and assume that the complexity of
![]() $(G,\Gamma ,G_\bullet )$
is at most
$(G,\Gamma ,G_\bullet )$
is at most
![]() $M_0$
. Then for each
$M_0$
. Then for each
![]() $N \in \mathbb {N}$
and each polynomial sequence
$N \in \mathbb {N}$
and each polynomial sequence
![]() $g \in \mathrm {poly}(\mathbb {Z},G_\bullet )$
there exists an integer M with
$g \in \mathrm {poly}(\mathbb {Z},G_\bullet )$
there exists an integer M with
![]() $M_0 \leq M \ll M_0^{O_{C,d,D}(1)}$
and a decomposition
$M_0 \leq M \ll M_0^{O_{C,d,D}(1)}$
and a decomposition
![]() $g(n) = \varepsilon (n) g'(n) \gamma (n)$
(
$g(n) = \varepsilon (n) g'(n) \gamma (n)$
(
![]() $n \in \mathbb {Z}$
), where
$n \in \mathbb {Z}$
), where
![]() $\varepsilon ,g',\gamma \in \mathrm {poly}(\mathbb {Z},G_\bullet )$
and
$\varepsilon ,g',\gamma \in \mathrm {poly}(\mathbb {Z},G_\bullet )$
and
-
(i) the sequence
 $( \varepsilon (n) )_{n=0}^{N-1}$
is
$( \varepsilon (n) )_{n=0}^{N-1}$
is
 $(M,N)$
-smooth;
$(M,N)$
-smooth; -
(ii) the sequence
 $( \gamma (n)\Gamma )_{n=0}^{N-1}$
is M-rational and periodic with period less than or equal to M;
$( \gamma (n)\Gamma )_{n=0}^{N-1}$
is M-rational and periodic with period less than or equal to M; -
(iii) there is a group
 $G' < G$
with Mal’cev basis
$G' < G$
with Mal’cev basis  in which each element is an M-rational combination of elements of
in which each element is an M-rational combination of elements of  such that
such that
 $g'(n) \in G'$
for all
$g'(n) \in G'$
for all
 $n \in \mathbb {Z}$
, and the sequence
$n \in \mathbb {Z}$
, and the sequence
 $( g'(n)\Gamma ' )_{n=0}^{N-1}$
is totally
$( g'(n)\Gamma ' )_{n=0}^{N-1}$
is totally
 $1/M^C$
-equidistributed in
$1/M^C$
-equidistributed in
 $G'/\Gamma '$
, where
$G'/\Gamma '$
, where
 $\Gamma ' = \Gamma \cap G'$
.
$\Gamma ' = \Gamma \cap G'$
.
4.4 Generalized polynomials
The connection between nilmanifolds and generalized polynomials was first elucidated by Bergelson and Leibman [Reference Bergelson and LeibmanBL07].
Theorem 4.2. [Reference Bergelson and LeibmanBL07]
Let
![]() $f \colon \mathbb {Z} \to [0,1)$
be a sequence. Then the following conditions are equivalent.
$f \colon \mathbb {Z} \to [0,1)$
be a sequence. Then the following conditions are equivalent.
-
(i) f is a GP map.
-
(ii) There exist a connected, simply connected nilpotent Lie group G, a lattice
 $\Gamma < G$
,
$\Gamma < G$
,
 $g \in G$
and a piecewise polynomial map
$g \in G$
and a piecewise polynomial map
 $F \colon G/\Gamma \to [0,1)$
such that
$F \colon G/\Gamma \to [0,1)$
such that
 $f(n) = F(g^n\Gamma )$
for all
$f(n) = F(g^n\Gamma )$
for all
 $n \in \mathbb {Z}$
.
$n \in \mathbb {Z}$
. -
(iii) There exist a connected, simply connected nilpotent Lie group G of some dimension D, a lattice
 $\Gamma < G$
, a compatible filtration
$\Gamma < G$
, a compatible filtration
 $G_\bullet $
, a polynomial sequence
$G_\bullet $
, a polynomial sequence
 ${g \in \mathrm {poly}(\mathbb {Z},G_\bullet )}$
and an index
${g \in \mathrm {poly}(\mathbb {Z},G_\bullet )}$
and an index
 $1 \leq j \leq D$
such that
$1 \leq j \leq D$
such that
 $f(n) = \tau _j(g(n)\Gamma )$
for all
$f(n) = \tau _j(g(n)\Gamma )$
for all
 $n \in \mathbb {Z}$
.
$n \in \mathbb {Z}$
.
Remark 4.3. Strictly speaking, [Reference Bergelson and LeibmanBL07] does not include the assumption that G should be connected and simply connected. However, this requirement can be ensured by replacing G with a larger group. (cf. the ‘lifting argument’ in [Reference FrantzikinakisFra09, pp. 368] and also [Reference Bergelson and LeibmanBL07, Theorem A*]). The cost of this operation is that in (ii) one may not assume that the action of g on
![]() $G/\Gamma $
is minimal, but we do not need this assumption.
$G/\Gamma $
is minimal, but we do not need this assumption.
In our applications, we will need to simultaneously represent maps of the form
![]() $f(\lfloor p(n) \rfloor )$
where f is a fixed GP map and p is a polynomial which is allowed to vary. Such a representation is readily obtained from Theorem 4.2.
$f(\lfloor p(n) \rfloor )$
where f is a fixed GP map and p is a polynomial which is allowed to vary. Such a representation is readily obtained from Theorem 4.2.
Theorem 4.4. Let
![]() $f \colon \mathbb {Z} \to \mathbb {R}$
be a bounded GP map and let
$f \colon \mathbb {Z} \to \mathbb {R}$
be a bounded GP map and let
![]() $d \in \mathbb {N}$
. Then there exist a connected, simply connected nilpotent Lie group G, a lattice
$d \in \mathbb {N}$
. Then there exist a connected, simply connected nilpotent Lie group G, a lattice
![]() $\Gamma < G$
, a filtration
$\Gamma < G$
, a filtration
![]() $G_\bullet $
, and a piecewise polynomial map
$G_\bullet $
, and a piecewise polynomial map
![]() $F \colon G/\Gamma \to \mathbb {Z}$
such that for each polynomial
$F \colon G/\Gamma \to \mathbb {Z}$
such that for each polynomial
![]() $p(x) \in \mathbb {R}[x]$
with
$p(x) \in \mathbb {R}[x]$
with
![]() $\deg p \leq d$
there exists
$\deg p \leq d$
there exists
![]() $g_p \in \mathrm {poly}(G_\bullet )$
such that for all
$g_p \in \mathrm {poly}(G_\bullet )$
such that for all
![]() $n \in \mathbb {Z}$
we have
$n \in \mathbb {Z}$
we have
![]() $f( \lfloor p(n) \rfloor ) = F(g_p(n)\Gamma )$
.
$f( \lfloor p(n) \rfloor ) = F(g_p(n)\Gamma )$
.
Proof. By Theorem 4.2, there exist a nilmanifold
![]() $G^{(0)}/\Gamma ^{(0)}$
together with a piecewise polynomial map
$G^{(0)}/\Gamma ^{(0)}$
together with a piecewise polynomial map
![]() $F^{(0)} \colon G^{(0)}/\Gamma ^{(0)} \to \mathbb {R}$
, and a group element
$F^{(0)} \colon G^{(0)}/\Gamma ^{(0)} \to \mathbb {R}$
, and a group element
![]() $g_0 \in G^{(0)}$
such that
$g_0 \in G^{(0)}$
such that
![]() ${f(n) = F^{(0)}(g_0^n \Gamma )}$
for all
${f(n) = F^{(0)}(g_0^n \Gamma )}$
for all
![]() $n \in \mathbb {Z}$
. Following the strategy in [Reference FrantzikinakisFra09, Lemma 4.1], let
$n \in \mathbb {Z}$
. Following the strategy in [Reference FrantzikinakisFra09, Lemma 4.1], let
![]() $G := G^{(0)} \times \mathbb {R}$
and
$G := G^{(0)} \times \mathbb {R}$
and
![]() $\Gamma := \Gamma ^{(0)} \times \mathbb {Z}$
, and let
$\Gamma := \Gamma ^{(0)} \times \mathbb {Z}$
, and let
![]() $F \colon G/\Gamma \to \mathbb {R}$
be given by
$F \colon G/\Gamma \to \mathbb {R}$
be given by
![]() $F(t + \mathbb {Z},h \Gamma ^{(0)}) := F^{(0)}( g_0^{-\{ t \} } h \Gamma ^{(0)})$
for
$F(t + \mathbb {Z},h \Gamma ^{(0)}) := F^{(0)}( g_0^{-\{ t \} } h \Gamma ^{(0)})$
for
![]() $t \in \mathbb {R}$
and
$t \in \mathbb {R}$
and
![]() $h \in G^{(0)}$
. This construction guarantees that F is piecewise polynomial and for all
$h \in G^{(0)}$
. This construction guarantees that F is piecewise polynomial and for all
![]() $t \in \mathbb {R}$
we have
$t \in \mathbb {R}$
we have
For
![]() $p \in \mathbb {R}[x]$
and
$p \in \mathbb {R}[x]$
and
![]() $n \in \mathbb {Z}$
let g
p
(n):= (p(n), g
0
p(n)). Then
$n \in \mathbb {Z}$
let g
p
(n):= (p(n), g
0
p(n)). Then
![]() $g_\alpha $
is polynomial with respect to the filtration
$g_\alpha $
is polynomial with respect to the filtration
![]() $G_\bullet $
given by
$G_\bullet $
given by
![]() $G_{i} = G_{(\lfloor i/d \rfloor )}$
, where
$G_{i} = G_{(\lfloor i/d \rfloor )}$
, where
![]() $( G_{(j)} )_j$
denotes the lower central series, and we have
$( G_{(j)} )_j$
denotes the lower central series, and we have
![]() $f( \lfloor p(n) \rfloor ) = F(g_p(n)\Gamma )$
for all
$f( \lfloor p(n) \rfloor ) = F(g_p(n)\Gamma )$
for all
![]() $n \in \mathbb {Z}$
.
$n \in \mathbb {Z}$
.
5 Möbius orthogonality
5.1 Main result
In this section, we discuss Möbius orthogonality of bracket words along Hardy field sequences. Our main result is Theorem B, which we restate below.
Theorem 5.1. Let
![]() ${\mathbf a} = (a(n))_{n \in \mathbb {Z}}$
be a (two-sided)
${\mathbf a} = (a(n))_{n \in \mathbb {Z}}$
be a (two-sided)
![]() $\mathbb {R}$
-valued bracket word and let
$\mathbb {R}$
-valued bracket word and let
![]() $f \colon \mathbb {R}_+ \to \mathbb {R}$
be a Hardy field function with polynomial growth. Then
$f \colon \mathbb {R}_+ \to \mathbb {R}$
be a Hardy field function with polynomial growth. Then
 $$ \begin{align} \frac{1}{N} \sum_{n=1}^N \mu(n) a( \lfloor f(n) \rfloor ) \to 0 \quad \text{as } N \to \infty. \end{align} $$
$$ \begin{align} \frac{1}{N} \sum_{n=1}^N \mu(n) a( \lfloor f(n) \rfloor ) \to 0 \quad \text{as } N \to \infty. \end{align} $$
As usual, we will use Taylor expansion to approximate the restriction of
![]() $f(n)$
to an interval with a polynomial sequence, and then use Theorem 2.11 to control the error term involved in computing
$f(n)$
to an interval with a polynomial sequence, and then use Theorem 2.11 to control the error term involved in computing
![]() $\lfloor f(n) \rfloor $
. The sequence
$\lfloor f(n) \rfloor $
. The sequence
![]() $a(\lfloor f(n) \rfloor )$
can then be represented on a nilmanifold by Bergelson–Leibman machinery. As the next step, we require a suitable result on Möbius orthogonality in short intervals. In §5.2, we will prove the following theorem, which is closely related to [Reference Matomäki, Shao, Tao and TeräväinenMSTT22, Theorem 1.1(i)]. Below, we let
$a(\lfloor f(n) \rfloor )$
can then be represented on a nilmanifold by Bergelson–Leibman machinery. As the next step, we require a suitable result on Möbius orthogonality in short intervals. In §5.2, we will prove the following theorem, which is closely related to [Reference Matomäki, Shao, Tao and TeräväinenMSTT22, Theorem 1.1(i)]. Below, we let
![]() $\mathcal {AP}$
denote the set of all arithmetic progressions in
$\mathcal {AP}$
denote the set of all arithmetic progressions in
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
Theorem 5.2. Let G be a connected, simply connected nilpotent Lie group, let
![]() $\Gamma < G$
be a lattice, let
$\Gamma < G$
be a lattice, let
![]() $G_\bullet $
be a filtration on G, assume that
$G_\bullet $
be a filtration on G, assume that
![]() $G_\bullet $
and
$G_\bullet $
and
![]() $\Gamma $
are compatible, and let
$\Gamma $
are compatible, and let
![]() $F \colon G/\Gamma \to \mathbb {R}$
be a finite-valued piecewise polynomial map. Let
$F \colon G/\Gamma \to \mathbb {R}$
be a finite-valued piecewise polynomial map. Let
![]() $N,H$
be integers with
$N,H$
be integers with
![]() $N^{0.626} \leq H \leq N$
. Then
$N^{0.626} \leq H \leq N$
. Then
where the rate of convergence may depend on
![]() $G,\Gamma ,G_\bullet $
and F.
$G,\Gamma ,G_\bullet $
and F.
Proof of Theorem 5.1 assuming Theorem 5.2
Applying a dyadic decomposition, it will suffice to show that
Fix a small
![]() $\varepsilon> 0$
. We will show that for all sufficiently large N we have
$\varepsilon> 0$
. We will show that for all sufficiently large N we have
Splitting the average in (16) into intervals of length
![]() $\lceil (2N)^{0.7} \rceil $
, we see that (16) will follow once we show that for sufficiently large N and for H satisfying
$\lceil (2N)^{0.7} \rceil $
, we see that (16) will follow once we show that for sufficiently large N and for H satisfying
![]() $N^{0.7} \leq H < N$
we have
$N^{0.7} \leq H < N$
we have
Pick an integer
![]() $k \in \mathbb {N}$
such that
$k \in \mathbb {N}$
such that
![]() $f(t) \ll t^k$
, and let
$f(t) \ll t^k$
, and let
![]() $\ell = 10 k$
. By Theorem 2.11, we have
$\ell = 10 k$
. By Theorem 2.11, we have
where
![]() $P_N$
is a polynomial of degree (at most)
$P_N$
is a polynomial of degree (at most)
![]() $\ell $
and one of the conditions (i)–(iii) in Theorem 2.11 holds. In the case (i) we have
$\ell $
and one of the conditions (i)–(iii) in Theorem 2.11 holds. In the case (i) we have
![]() $N \ll _{\varepsilon } H^{10/9} \leq N^{7/9}$
, which implies that
$N \ll _{\varepsilon } H^{10/9} \leq N^{7/9}$
, which implies that
![]() ${N = O_\varepsilon (1)}$
. Assuming that N is sufficiently large, we may disregard this case.
${N = O_\varepsilon (1)}$
. Assuming that N is sufficiently large, we may disregard this case.
In case (ii) we have
![]() ${\mathbb {E}}_{h < H} |e_N(h)| < \varepsilon $
, and as a consequence
${\mathbb {E}}_{h < H} |e_N(h)| < \varepsilon $
, and as a consequence
By Theorem 4.4, there exist a connected and simply connected nilpotent Lie group G, a lattice
![]() $\Gamma < G$
, a filtration
$\Gamma < G$
, a filtration
![]() $G_\bullet $
and a finite-valued piecewise polynomial map
$G_\bullet $
and a finite-valued piecewise polynomial map
![]() $F \colon G/\Gamma \to \mathbb {Z}$
such that for each polynomial P of degree at most
$F \colon G/\Gamma \to \mathbb {Z}$
such that for each polynomial P of degree at most
![]() $\ell $
there exists
$\ell $
there exists
![]() $g \in \mathrm {poly}(G_\bullet )$
such that
$g \in \mathrm {poly}(G_\bullet )$
such that
![]() $a(\lfloor P(h) \rfloor ) = F(g(h)\Gamma )$
; it is crucial that we have the same
$a(\lfloor P(h) \rfloor ) = F(g(h)\Gamma )$
; it is crucial that we have the same
![]() $(G,\Gamma , G_{\bullet })$
for all polynomials P. In particular,
$(G,\Gamma , G_{\bullet })$
for all polynomials P. In particular,
By Theorem 5.2 (which is uniform in g), for sufficiently large N the expression in (20) is bounded by
![]() $\varepsilon $
. Inserting this bound into (19) yields (17).
$\varepsilon $
. Inserting this bound into (19) yields (17).
In case (iii), passing to an arithmetic progression, we may replace
![]() $e_N$
with a constant sequence:
$e_N$
with a constant sequence:
To finish the argument, it suffices to apply Theorem 5.2 similarly to the previous case.
5.2 Short intervals
The remainder of this section is devoted to proving Theorem 5.2. We will derive it from closely related estimates for correlations of the Möbius function with nilsequences in short intervals. Recall that we let
![]() $\mathcal {AP}$
denote the set of all arithmetic progressions in
$\mathcal {AP}$
denote the set of all arithmetic progressions in
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
Theorem 5.3. (Corollary of [Reference Matomäki, Shao, Tao and TeräväinenMSTT22, Theorem 1.1(i)])
Let
![]() $N,H$
be integers with
$N,H$
be integers with
![]() $N^{0.626} \leq H \leq N$
and let
$N^{0.626} \leq H \leq N$
and let
![]() $\delta \in (0,1/2)$
. Let G be a connected, simply connected nilpotent Lie group of dimension D, let
$\delta \in (0,1/2)$
. Let G be a connected, simply connected nilpotent Lie group of dimension D, let
![]() $\Gamma < G$
be a lattice, let
$\Gamma < G$
be a lattice, let
![]() $G_\bullet $
be a nilpotent filtration on G of length d, and assume that the complexity of
$G_\bullet $
be a nilpotent filtration on G of length d, and assume that the complexity of
![]() $(G,\Gamma ,G_\bullet )$
is at most
$(G,\Gamma ,G_\bullet )$
is at most
![]() $1/\delta $
. Let
$1/\delta $
. Let
![]() $F \colon G/\Gamma \to \mathbb {C}$
be a function with Lipschitz norm at most
$F \colon G/\Gamma \to \mathbb {C}$
be a function with Lipschitz norm at most
![]() $1/\delta $
. Then for each
$1/\delta $
. Then for each
![]() $A> 0$
we have the bound
$A> 0$
we have the bound

This theorem is almost the ingredient that we need, except that in our application the function F is not necessarily continuous (much less Lipschitz). Instead, F is a finite-valued piecewise polynomial function, meaning that there exists a partition
![]() $G/\Gamma = \bigcup _{i=1}^r S_i$
into semialgebraic pieces and constants
$G/\Gamma = \bigcup _{i=1}^r S_i$
into semialgebraic pieces and constants
![]() $c_i \in \mathbb {R}$
such that for each
$c_i \in \mathbb {R}$
such that for each
![]() $x \in X$
and
$x \in X$
and
![]() $1 \leq i \leq r$
,
$1 \leq i \leq r$
,
![]() $F(x) = c_i$
if and only if
$F(x) = c_i$
if and only if
![]() $x \in S_i$
. In this case, it is enough to consider each of the level sets separately. It is clear that Theorem 5.2 will follow from the following more precise result.
$x \in S_i$
. In this case, it is enough to consider each of the level sets separately. It is clear that Theorem 5.2 will follow from the following more precise result.
Theorem 5.4. Let
![]() $N,H$
be integers with
$N,H$
be integers with
![]() $N^{0.626} \leq H \leq N$
and let
$N^{0.626} \leq H \leq N$
and let
![]() $\delta \in (0,1/2)$
. Let G be a connected, simply connected nilpotent Lie group of dimension D, let
$\delta \in (0,1/2)$
. Let G be a connected, simply connected nilpotent Lie group of dimension D, let
![]() $\Gamma < G$
be a lattice, let
$\Gamma < G$
be a lattice, let
![]() $G_\bullet $
be a nilpotent filtration on G of length d, and assume that the complexity of
$G_\bullet $
be a nilpotent filtration on G of length d, and assume that the complexity of
![]() $(G,\Gamma ,G_\bullet )$
is at most
$(G,\Gamma ,G_\bullet )$
is at most
![]() $1/\delta $
. Let
$1/\delta $
. Let
![]() $S \subseteq G/\Gamma $
be a semialgebraic set with complexity at most E. Then for each
$S \subseteq G/\Gamma $
be a semialgebraic set with complexity at most E. Then for each
![]() $A \geq 1$
we have the bound
$A \geq 1$
we have the bound

In the case where
![]() $(g(n)\Gamma )_n$
is highly equidistributed in
$(g(n)\Gamma )_n$
is highly equidistributed in
![]() $G/\Gamma $
, we will derive Theorem 5.4 directly from Theorem 5.3. In fact, we will obtain a slightly stronger version, given in Proposition 5.6 below. Then we will deduce the general case of Theorem 5.4 using the factorization theorem from [Reference Green and TaoGT12b]. In order to avoid unnecessarily obfuscating the notation, from this point onwards we will allow all implicit constants to depend on the parameters d, D and E; thus, for instance, the term on the right-hand side of (24) will be more succinctly written as
$G/\Gamma $
, we will derive Theorem 5.4 directly from Theorem 5.3. In fact, we will obtain a slightly stronger version, given in Proposition 5.6 below. Then we will deduce the general case of Theorem 5.4 using the factorization theorem from [Reference Green and TaoGT12b]. In order to avoid unnecessarily obfuscating the notation, from this point onwards we will allow all implicit constants to depend on the parameters d, D and E; thus, for instance, the term on the right-hand side of (24) will be more succinctly written as
![]() ${ (1/\delta )^{O(1)}}/{\log ^A N}$
.
${ (1/\delta )^{O(1)}}/{\log ^A N}$
.
5.3 Equidistributed case
Before we proceed, we will need the following technical lemma.
Lemma 5.5. Let
![]() $d,D \in \mathbb {N}$
, and let
$d,D \in \mathbb {N}$
, and let
![]() $\mathcal {V}$
denote the vector space of all polynomial maps
$\mathcal {V}$
denote the vector space of all polynomial maps
![]() $P \colon [0,1)^D \to \mathbb {R}$
of degree at most d.
$P \colon [0,1)^D \to \mathbb {R}$
of degree at most d.
-
(i) There is a constant
 $C> 1$
(dependent on
$C> 1$
(dependent on
 $d,D$
) such that for
$d,D$
) such that for
 $P \in \mathcal {V}$
given by we have the inequalities C −1∥P∥ ∞ ≤ max α |a α |≤ C∥P∥ ∞ .
$P \in \mathcal {V}$
given by we have the inequalities C −1∥P∥ ∞ ≤ max α |a α |≤ C∥P∥ ∞ . $$ \begin{align*} P(x) = \sum_{\alpha \in \mathbb{N}_0^D} a_\alpha \prod_{i=1}^D x_i^{\alpha_i}, \end{align*} $$
$$ \begin{align*} P(x) = \sum_{\alpha \in \mathbb{N}_0^D} a_\alpha \prod_{i=1}^D x_i^{\alpha_i}, \end{align*} $$
-
(ii) For each
 $P \in \mathcal {V}$
and for each
$P \in \mathcal {V}$
and for each
 $\delta \in (0,1)$
we have (25)
$\delta \in (0,1)$
we have (25) $$ \begin{align} \unicode{x3bb}( \{ x \in [0,1)^D \mid |P(x)| < \delta^d\lVert P \rVert_\infty \} ) \ll_{d,D} \delta. \end{align} $$
$$ \begin{align} \unicode{x3bb}( \{ x \in [0,1)^D \mid |P(x)| < \delta^d\lVert P \rVert_\infty \} ) \ll_{d,D} \delta. \end{align} $$
Proof. Item (i) follows from the fact that each pair of norms on the finite-dimensional vector space
![]() $\mathcal {V}$
are equivalent. For item (ii) we proceed by induction with respect to D. Multiplying P by a scalar, we may assume that
$\mathcal {V}$
are equivalent. For item (ii) we proceed by induction with respect to D. Multiplying P by a scalar, we may assume that
![]() $\lVert P \rVert _\infty = 1$
.
$\lVert P \rVert _\infty = 1$
.
Suppose first that
![]() $D = 1$
. We proceed by induction on d. If
$D = 1$
. We proceed by induction on d. If
![]() $d = 1$
then P is an affine function
$d = 1$
then P is an affine function
![]() $P(x) = a x + b$
, and the claim follows easily. Assume that
$P(x) = a x + b$
, and the claim follows easily. Assume that
![]() $d \geq 2$
and that the claim has been proved for
$d \geq 2$
and that the claim has been proved for
![]() $d-1$
. By item (i), at least one of the coefficients of P has absolute value
$d-1$
. By item (i), at least one of the coefficients of P has absolute value
![]() $\gg _{d,D} 1$
. In fact, we may assume that this coefficient is not the constant term, since otherwise for all
$\gg _{d,D} 1$
. In fact, we may assume that this coefficient is not the constant term, since otherwise for all
![]() $x \in [0,1)$
we would have
$x \in [0,1)$
we would have
![]() $P(x) \in (\frac {99}{100}P(0),\frac {101}{100}P(0))$
and hence the set in (25) would be empty for sufficiently small
$P(x) \in (\frac {99}{100}P(0),\frac {101}{100}P(0))$
and hence the set in (25) would be empty for sufficiently small
![]() $\delta $
. Thus,
$\delta $
. Thus,
![]() $\lVert P' \rVert _\infty \gg _{d,D} 1$
. By the inductive assumption,
$\lVert P' \rVert _\infty \gg _{d,D} 1$
. By the inductive assumption,
Thus, it will suffice to show that
For each interval
![]() $I \subseteq [0,1)$
such that
$I \subseteq [0,1)$
such that
![]() $P'(x)$
has constant sign for
$P'(x)$
has constant sign for
![]() $x \in I$
, we have
$x \in I$
, we have
Since
![]() $[0,1)$
can be divided into
$[0,1)$
can be divided into
![]() $O(d)$
intervals where P is monotone, (27) follows.
$O(d)$
intervals where P is monotone, (27) follows.
Suppose now that
![]() $D \geq 2$
and the claim has been proved for all
$D \geq 2$
and the claim has been proved for all
![]() $D' < D$
. Reasoning as above, we infer from item (i) that P has a coefficient with absolute value
$D' < D$
. Reasoning as above, we infer from item (i) that P has a coefficient with absolute value
![]() $\gg _{d,D} 1$
other than the constant. We may expand P as
$\gg _{d,D} 1$
other than the constant. We may expand P as
 $$ \begin{align*} P(y,t) &= \sum_{i=0}^{d} t^{i} Q_i(y), \quad y \in [0,1)^{D-1},\ t \in [0,1), \end{align*} $$
$$ \begin{align*} P(y,t) &= \sum_{i=0}^{d} t^{i} Q_i(y), \quad y \in [0,1)^{D-1},\ t \in [0,1), \end{align*} $$
where the
![]() $Q_i$
are polynomials in
$Q_i$
are polynomials in
![]() $D-1$
variables of degree
$D-1$
variables of degree
![]() $d-i$
. Changing the order of variables if necessary, we may assume that there exists j with
$d-i$
. Changing the order of variables if necessary, we may assume that there exists j with
![]() $1 \leq j \leq d$
such that
$1 \leq j \leq d$
such that
![]() $Q_j$
has a coefficient
$Q_j$
has a coefficient
![]() $\gg _{d,D} 1$
, and hence
$\gg _{d,D} 1$
, and hence
![]() $\lVert Q_j \rVert _{\infty } \gg _{d,D} 1$
. For
$\lVert Q_j \rVert _{\infty } \gg _{d,D} 1$
. For
![]() $k \in \mathbb {N}$
, let us consider the set
$k \in \mathbb {N}$
, let us consider the set
The set in (28) is the disjoint union
![]() $\bigcup _{k=1}^\infty E_i$
, so our goal is to show that
$\bigcup _{k=1}^\infty E_i$
, so our goal is to show that
 $$ \begin{align} \sum_{k=1}^\infty \unicode{x3bb}(E_k) \ll_{d,D} \delta. \end{align} $$
$$ \begin{align} \sum_{k=1}^\infty \unicode{x3bb}(E_k) \ll_{d,D} \delta. \end{align} $$
Fix a value of k. By the inductive assumption, as long as
![]() $j \neq d$
, we have
$j \neq d$
, we have
(If
![]() $j = d$
, the set in (30) is empty for all sufficiently large k, and the reasoning simplifies.) For each
$j = d$
, the set in (30) is empty for all sufficiently large k, and the reasoning simplifies.) For each
![]() $y \in [0,1)^{D-1}$
such that
$y \in [0,1)^{D-1}$
such that
![]() $2^{-k} \leq |Q_j(y)| < 2^{-k+1}$
, by the inductive assumption (for
$2^{-k} \leq |Q_j(y)| < 2^{-k+1}$
, by the inductive assumption (for
![]() $D=1$
) we have
$D=1$
) we have
Combining (30) and (31) yields
We are now ready to prove a variant of Theorem 5.2 concerning highly equidistributed polynomial sequences on nilmanifolds. For technical reasons which will become clear in the next section, it will be convenient to consider more general type of averages, where instead of a factor of the form
![]() $1_S( g(h)\Gamma )$
with semialgebraic
$1_S( g(h)\Gamma )$
with semialgebraic
![]() $S \subseteq G/\Gamma $
we have a factor of the form
$S \subseteq G/\Gamma $
we have a factor of the form
![]() $1_S( {h}/{H},g(h)\Gamma )$
with semialgebraic
$1_S( {h}/{H},g(h)\Gamma )$
with semialgebraic
![]() $S \subseteq (\mathbb {R} /\mathbb {Z}) \times (G/\Gamma )$
; thus, in addition to the highly equidistributed sequence
$S \subseteq (\mathbb {R} /\mathbb {Z}) \times (G/\Gamma )$
; thus, in addition to the highly equidistributed sequence
![]() $g(h)\Gamma $
, we keep track of how large h is compared to H.
$g(h)\Gamma $
, we keep track of how large h is compared to H.
Proposition 5.6. Let
![]() $N,H$
be integers with
$N,H$
be integers with
![]() $N^{0.626} \leq H \leq N$
and let
$N^{0.626} \leq H \leq N$
and let
![]() $\delta \in (0,1/2)$
. Let G be a connected, simply connected nilpotent Lie group of dimension D, let
$\delta \in (0,1/2)$
. Let G be a connected, simply connected nilpotent Lie group of dimension D, let
![]() $\Gamma < G$
be a lattice, let
$\Gamma < G$
be a lattice, let
![]() $G_\bullet $
be a nilpotent filtration on G of length d, and assume that the complexity of
$G_\bullet $
be a nilpotent filtration on G of length d, and assume that the complexity of
![]() $(G,\Gamma ,G_\bullet )$
is at most
$(G,\Gamma ,G_\bullet )$
is at most
![]() $1/\delta $
. Let
$1/\delta $
. Let
![]() $S \subseteq (\mathbb {R}/\mathbb {Z}) \times (G/\Gamma )$
be a semialgebraic set with complexity at most E. Then for each
$S \subseteq (\mathbb {R}/\mathbb {Z}) \times (G/\Gamma )$
be a semialgebraic set with complexity at most E. Then for each
![]() $A \geq 1$
, there exists
$A \geq 1$
, there exists
![]() $B = O(A)$
such that
$B = O(A)$
such that

where
![]() $\widetilde \delta := 1/\log ^B{N}$
and the supremum is taken over all polynomial sequences g such that
$\widetilde \delta := 1/\log ^B{N}$
and the supremum is taken over all polynomial sequences g such that
![]() $( g(h)\Gamma )_{h =0}^H$
is totally
$( g(h)\Gamma )_{h =0}^H$
is totally
![]() $\widetilde \delta $
-equidistributed (t.e.d.).
$\widetilde \delta $
-equidistributed (t.e.d.).
Proof. We may freely assume that
![]() $\delta \geq 1/\log ^A N$
, since otherwise there is nothing to prove. In particular,
$\delta \geq 1/\log ^A N$
, since otherwise there is nothing to prove. In particular,
![]() $\delta = \log ^{O(A)}N$
and
$\delta = \log ^{O(A)}N$
and
![]() $1/\delta = O(\log ^A N)$
. Decomposing S into a bounded number of pieces, we may assume that S is a basic semialgebraic set. We will assume that
$1/\delta = O(\log ^A N)$
. Decomposing S into a bounded number of pieces, we may assume that S is a basic semialgebraic set. We will assume that
![]() $\operatorname {int} S \neq \emptyset $
; the case where
$\operatorname {int} S \neq \emptyset $
; the case where
![]() $\operatorname {int} S = \emptyset $
can be handled using similar methods and is somewhat simpler. Thus, S takes the form
$\operatorname {int} S = \emptyset $
can be handled using similar methods and is somewhat simpler. Thus, S takes the form
where
![]() $r = O(1)$
and
$r = O(1)$
and
![]() $P_i$
are polynomial maps (under identification of
$P_i$
are polynomial maps (under identification of
![]() $(\mathbb {R}/\mathbb {Z}) \times (G/\Gamma )$
with
$(\mathbb {R}/\mathbb {Z}) \times (G/\Gamma )$
with
![]() $[0,1)^{1+D}$
) with
$[0,1)^{1+D}$
) with
![]() $\deg P_i = O(1)$
for
$\deg P_i = O(1)$
for
![]() $1 \leq i \leq r$
. Scaling, we may assume that
$1 \leq i \leq r$
. Scaling, we may assume that
![]() ${\lVert P_i \rVert _\infty = 1}$
for all
${\lVert P_i \rVert _\infty = 1}$
for all
![]() $1 \leq i \leq r$
. Let
$1 \leq i \leq r$
. Let
![]() $\tau _1$
denote Mal’cev coordinates on
$\tau _1$
denote Mal’cev coordinates on
![]() $(\mathbb {R}/\mathbb {Z}) \times (G/\Gamma )$
, given by
$(\mathbb {R}/\mathbb {Z}) \times (G/\Gamma )$
, given by
![]() $\tau _1(t ,x) = (t,\tau (x))$
, where we identify
$\tau _1(t ,x) = (t,\tau (x))$
, where we identify
![]() $[0,1)$
with
$[0,1)$
with
![]() $\mathbb {R}/\mathbb {Z}$
in the standard way. Furthermore, splitting S further and applying a translation if necessary, we may assume that
$\mathbb {R}/\mathbb {Z}$
in the standard way. Furthermore, splitting S further and applying a translation if necessary, we may assume that
![]() $\tau _1(S) \subseteq ( \frac {1}{10},\frac {9}{10} )^{1+D}$
, implying in particular that
$\tau _1(S) \subseteq ( \frac {1}{10},\frac {9}{10} )^{1+D}$
, implying in particular that
![]() $\tau _1$
is continuous in a neighbourhood of S.
$\tau _1$
is continuous in a neighbourhood of S.
Let
![]() $\eta \in (0,\delta )$
be a small positive quantity, to be specified in the course of the argument, and let
$\eta \in (0,\delta )$
be a small positive quantity, to be specified in the course of the argument, and let
![]() $\Psi ,\Psi ' \colon \mathbb {R} \to [0,1]$
be given by
$\Psi ,\Psi ' \colon \mathbb {R} \to [0,1]$
be given by
 $$ \begin{align*} \Psi(t) = \begin{cases} 0 & \text{if } t < 0,\\ t/\eta & \text{if } t \in [0,\eta],\\ 1 & \text{if } t> \eta, \end{cases} \quad \Psi'(t) = \begin{cases} 0 & \text{if } |t| > 2\eta,\\ 2- |t|/\eta & \text{if } |t| \in [\eta,2\eta],\\ 1 & \text{if } |t| < \eta. \end{cases} \end{align*} $$
$$ \begin{align*} \Psi(t) = \begin{cases} 0 & \text{if } t < 0,\\ t/\eta & \text{if } t \in [0,\eta],\\ 1 & \text{if } t> \eta, \end{cases} \quad \Psi'(t) = \begin{cases} 0 & \text{if } |t| > 2\eta,\\ 2- |t|/\eta & \text{if } |t| \in [\eta,2\eta],\\ 1 & \text{if } |t| < \eta. \end{cases} \end{align*} $$
It is clear that
![]() $\lVert \Psi \rVert _{\mathrm {Lip}} = \lVert \Psi ' \rVert _{\mathrm {Lip}} = 1/\eta $
. Let
$\lVert \Psi \rVert _{\mathrm {Lip}} = \lVert \Psi ' \rVert _{\mathrm {Lip}} = 1/\eta $
. Let
![]() $\Psi _{\square } \colon [0,1)^{1+D} \to [0,1]$
be an
$\Psi _{\square } \colon [0,1)^{1+D} \to [0,1]$
be an
![]() $O(1)$
-Lipschitz function with
$O(1)$
-Lipschitz function with
![]() $\Psi _{\square }(t,u) = 1$
if
$\Psi _{\square }(t,u) = 1$
if
![]() $(t,u) \in ( \frac {1}{10},\frac {9}{10} )^{1+D}$
and
$(t,u) \in ( \frac {1}{10},\frac {9}{10} )^{1+D}$
and
![]() $\Psi _{\square }(t,u) = 0$
if
$\Psi _{\square }(t,u) = 0$
if
![]() $(t,u) \not \in ( \frac {1}{20},\frac {19}{20} )^{1+D}$
. For
$(t,u) \not \in ( \frac {1}{20},\frac {19}{20} )^{1+D}$
. For
![]() $1 \leq i \leq r$
, put
$1 \leq i \leq r$
, put
 $$ \begin{align*} F_i(t,x) &= \Psi(P_i(t,x)), \quad F_i'(t,x) = \Psi_{\square}(\tau_1(t,x))\Psi'(P_i(t,x)),\\[-1pt] F(t,x) &= \prod_{i=1}^r F_i(t,x), \quad F'(t,x) = \min\bigg( \sum_{i=1}^r F_i'(t,x),1 \bigg). \end{align*} $$
$$ \begin{align*} F_i(t,x) &= \Psi(P_i(t,x)), \quad F_i'(t,x) = \Psi_{\square}(\tau_1(t,x))\Psi'(P_i(t,x)),\\[-1pt] F(t,x) &= \prod_{i=1}^r F_i(t,x), \quad F'(t,x) = \min\bigg( \sum_{i=1}^r F_i'(t,x),1 \bigg). \end{align*} $$
It is routine (although tedious) to verify that F and
![]() $F'$
are
$F'$
are
![]() $1/\eta ^{O(1)}$
-Lipschitz (cf. [Reference Green and TaoGT12b, Lemma A.4]); this follows from the aforementioned bounds on the Lipschitz norms of
$1/\eta ^{O(1)}$
-Lipschitz (cf. [Reference Green and TaoGT12b, Lemma A.4]); this follows from the aforementioned bounds on the Lipschitz norms of
![]() $\Psi $
and
$\Psi $
and
![]() $\Psi '$
and the fact that the derivatives of the polynomials
$\Psi '$
and the fact that the derivatives of the polynomials
![]() $P_i$
are bounded by
$P_i$
are bounded by
![]() $O(1)$
on
$O(1)$
on
![]() $[0,1)^{D+1}$
, which follows, for example, from Lemma 5.5. Directly from the definitions, we see that for each
$[0,1)^{D+1}$
, which follows, for example, from Lemma 5.5. Directly from the definitions, we see that for each
![]() $t \in \mathbb {R}/\mathbb {Z}$
and
$t \in \mathbb {R}/\mathbb {Z}$
and
![]() $x \in G/\Gamma $
we have
$x \in G/\Gamma $
we have
![]() $F(t,x) = 1_S(t,x)$
or
$F(t,x) = 1_S(t,x)$
or
![]() $F'(t,x) = 1$
. It follows that
$F'(t,x) = 1$
. It follows that

In order to estimate either of the summands in (35), we begin by dividing the interval
![]() $[H]$
into
$[H]$
into
![]() $O(1/\alpha )$
subintervals with lengths between
$O(1/\alpha )$
subintervals with lengths between
![]() $\alpha H$
and
$\alpha H$
and
![]() $2\alpha H$
, where
$2\alpha H$
, where
To estimate the first summand, we note that for each such subinterval
![]() $[k ,k +H')$
(where
$[k ,k +H')$
(where
![]() $\alpha H \leq H' < 2\alpha H < H$
), for each
$\alpha H \leq H' < 2\alpha H < H$
), for each
![]() $h \in [k ,k +H')$
, we have
$h \in [k ,k +H')$
, we have
 $$ \begin{align} F\bigg( \frac{h}{H},g(h)\Gamma \bigg) &= F\bigg( \frac{k}{H},g(h)\Gamma \bigg) + O\bigg( \frac{H'}{H} \lVert F \rVert_{\mathrm{Lip}} \bigg)\nonumber\\& = F\bigg( \frac{k}{H},g(h)\Gamma \bigg) + O\bigg( \frac{1}{\log^A N} \bigg). \end{align} $$
$$ \begin{align} F\bigg( \frac{h}{H},g(h)\Gamma \bigg) &= F\bigg( \frac{k}{H},g(h)\Gamma \bigg) + O\bigg( \frac{H'}{H} \lVert F \rVert_{\mathrm{Lip}} \bigg)\nonumber\\& = F\bigg( \frac{k}{H},g(h)\Gamma \bigg) + O\bigg( \frac{1}{\log^A N} \bigg). \end{align} $$
Applying Theorem 5.3 to each subinterval, for each constant
![]() $C \geq 1$
we obtain
$C \geq 1$
we obtain

Let us now consider the second summand. We have, similarly to (37),
 $$ \begin{align*} F'\bigg( \frac{h}{H},g(h)\Gamma \bigg) = F'\bigg( \frac{k}{H},g(h)\Gamma \bigg) + O\bigg( \frac{1}{\log^A N} \bigg). \end{align*} $$
$$ \begin{align*} F'\bigg( \frac{h}{H},g(h)\Gamma \bigg) = F'\bigg( \frac{k}{H},g(h)\Gamma \bigg) + O\bigg( \frac{1}{\log^A N} \bigg). \end{align*} $$
For now, let us assume that
![]() $\alpha> \widetilde \delta $
, which we will verify at the end of the argument. We conclude from the fact that
$\alpha> \widetilde \delta $
, which we will verify at the end of the argument. We conclude from the fact that
![]() $(g(h)\Gamma )_{h =0}^{H-1}$
is totally
$(g(h)\Gamma )_{h =0}^{H-1}$
is totally
![]() $\widetilde \delta $
-equidistributed that
$\widetilde \delta $
-equidistributed that

where we use
![]() $dx$
as a shorthand for
$dx$
as a shorthand for
![]() $d \mu _{G/\Gamma }(x)$
. Taking the weighted average of (39) over all subintervals, we conclude that
$d \mu _{G/\Gamma }(x)$
. Taking the weighted average of (39) over all subintervals, we conclude that

Applying Lemma 5.5(ii) to estimate the measure of the support of
![]() $F_i'$
for each
$F_i'$
for each
![]() $1 \leq i \leq r$
, we conclude that
$1 \leq i \leq r$
, we conclude that
 $$ \begin{align} \int_{[0,1)} \int_{G/\Gamma} F'(t,x) \,dx dt \ll \eta^{1/O(1)}. \end{align} $$
$$ \begin{align} \int_{[0,1)} \int_{G/\Gamma} F'(t,x) \,dx dt \ll \eta^{1/O(1)}. \end{align} $$
Thus, we may choose
![]() $\eta = 1/\log ^{O(A)} N$
such that
$\eta = 1/\log ^{O(A)} N$
such that
 $$ \begin{align} \int_{[0,1)} \int_{G/\Gamma}F'(t,x) \,dx dt \leq \frac{1}{\log^A N}, \end{align} $$
$$ \begin{align} \int_{[0,1)} \int_{G/\Gamma}F'(t,x) \,dx dt \leq \frac{1}{\log^A N}, \end{align} $$
which allows us to simplify (40) to

Combining (38) and (43) with (35), we conclude that

Letting C and B be sufficiently large multiples of A, we conclude that

as needed. Note that choosing B as a large multiple of A also guarantees that
![]() ${\alpha = 1{/}\kern1pt{\log} ^{O(A)}N> \widetilde \delta = 1{/}\kern1pt{\log} ^B N}$
.
${\alpha = 1{/}\kern1pt{\log} ^{O(A)}N> \widetilde \delta = 1{/}\kern1pt{\log} ^B N}$
.
5.4 General case
We now have all the ingredients necessary to complete the proof.
Proof of Theorem 5.4
The argument is very similar to the proof of Theorem 1.1, assuming [Reference Green and TaoGT12a, Proposition 2.1]. As the first step, we apply the factorization theorem [Reference Green and TaoGT12b, Theorem 1.19], Theorem 4.1 above, with
![]() $M_0 = \log N$
and parameter C to be determined in the course of the argument. We conclude that there exists an integer M with
$M_0 = \log N$
and parameter C to be determined in the course of the argument. We conclude that there exists an integer M with
![]() $\log N \leq M \ll \log ^{O_C(1)}N$
such that g admits a factorization of the form
$\log N \leq M \ll \log ^{O_C(1)}N$
such that g admits a factorization of the form
where
![]() $\varepsilon $
is
$\varepsilon $
is
![]() $(M,N)$
-smooth,
$(M,N)$
-smooth,
![]() $\gamma $
is M-rational, and
$\gamma $
is M-rational, and
![]() $g'$
takes values in a rational subgroup
$g'$
takes values in a rational subgroup
![]() $G' < G$
which admits a Mal’cev basis
$G' < G$
which admits a Mal’cev basis ![]() where each element is an M-rational combination of elements of
where each element is an M-rational combination of elements of ![]() , and
, and
![]() $(g'(h)\Gamma )_{h =0}^{H-1}$
is totally
$(g'(h)\Gamma )_{h =0}^{H-1}$
is totally
![]() $1/M^{C}$
-equidistributed in
$1/M^{C}$
-equidistributed in
![]() $G'/(\Gamma \cap G')$
(with respect to the metric induced by
$G'/(\Gamma \cap G')$
(with respect to the metric induced by ![]() ).
).
With the same reasoning as in [Reference Green and TaoGT12a], we conclude that
![]() $(\gamma (h)\Gamma )_h$
is a periodic sequence with some period
$(\gamma (h)\Gamma )_h$
is a periodic sequence with some period
![]() $q \leq M$
, and for each
$q \leq M$
, and for each
![]() $0 \leq j < q$
and
$0 \leq j < q$
and
![]() $h \equiv j \bmod q$
we have
$h \equiv j \bmod q$
we have
![]() $\gamma (h) \Gamma = \gamma _j \Gamma $
for some
$\gamma (h) \Gamma = \gamma _j \Gamma $
for some
![]() $\gamma _j \in G$
with coordinates
$\gamma _j \in G$
with coordinates
![]() $\tau (\gamma _j)$
that are rationals with height much less than
$\tau (\gamma _j)$
that are rationals with height much less than
![]() $ M^{O(1)}$
. Splitting the average in (24) into subprogressions, it will suffice to show that for each residue
$ M^{O(1)}$
. Splitting the average in (24) into subprogressions, it will suffice to show that for each residue
![]() $0 \leq j < q$
modulo q, and for each arithmetic progression
$0 \leq j < q$
modulo q, and for each arithmetic progression
![]() $Q \subseteq q \mathbb {Z} + j$
with diameter at most
$Q \subseteq q \mathbb {Z} + j$
with diameter at most
![]() $N/M$
, we have
$N/M$
, we have

The key difference between our current work and the corresponding argument in [Reference Green and TaoGT12a] is that
![]() $1_S$
is not continuous and hence in (47) we cannot replace
$1_S$
is not continuous and hence in (47) we cannot replace
![]() $\varepsilon (h)$
with a constant and hope that the value of the average will remain approximately unchanged. Instead, we will use an argument of a more algebraic type. We note that, as a consequence of invariance of the metric on G under multiplication on the right, for each
$\varepsilon (h)$
with a constant and hope that the value of the average will remain approximately unchanged. Instead, we will use an argument of a more algebraic type. We note that, as a consequence of invariance of the metric on G under multiplication on the right, for each
![]() $h,h' \in Q$
we have
$h,h' \in Q$
we have
Let us fix
![]() $k \in Q$
and put
$k \in Q$
and put
![]() $\varepsilon '(h) = \varepsilon (h)\varepsilon (k )^{-1}$
. Then
$\varepsilon '(h) = \varepsilon (h)\varepsilon (k )^{-1}$
. Then
![]() $d(\varepsilon '(h),e_G) = O(1)$
and
$d(\varepsilon '(h),e_G) = O(1)$
and
![]() $g(h)\Gamma = \varepsilon (h) g'(h) \gamma _j \Gamma = \varepsilon '(h) \varepsilon (k )g'(h)\gamma _j\Gamma $
.
$g(h)\Gamma = \varepsilon (h) g'(h) \gamma _j \Gamma = \varepsilon '(h) \varepsilon (k )g'(h)\gamma _j\Gamma $
.
Let
![]() $\Omega \subseteq G$
be a bounded semialgebraic set such that
$\Omega \subseteq G$
be a bounded semialgebraic set such that
![]() $\varepsilon '(h) \in \Omega $
for all
$\varepsilon '(h) \in \Omega $
for all
![]() $h \in Q$
. For instance, we may take
$h \in Q$
. For instance, we may take
![]() $\Omega $
to be the preimage of a certain ball with radius
$\Omega $
to be the preimage of a certain ball with radius
![]() $1/\delta ^{O(1)}$
under
$1/\delta ^{O(1)}$
under
![]() $\widetilde \tau $
. Let also
$\widetilde \tau $
. Let also
![]() $\Pi := \widetilde \tau ^{-1}( [0,1)^D )$
denote the standard fundamental domain for
$\Pi := \widetilde \tau ^{-1}( [0,1)^D )$
denote the standard fundamental domain for
![]() $G/\Gamma $
. Consider the set
$G/\Gamma $
. Consider the set
We may decompose R as
 $$ \begin{align} R = \bigcup_{\gamma \in \Gamma} R_\gamma \quad\text{where } R_\gamma = \{ (g_1,g_2) \in \Omega \times \Pi \mid g_1g_2 \Gamma \in S,\ g_1g_2\gamma \in \Pi \}. \end{align} $$
$$ \begin{align} R = \bigcup_{\gamma \in \Gamma} R_\gamma \quad\text{where } R_\gamma = \{ (g_1,g_2) \in \Omega \times \Pi \mid g_1g_2 \Gamma \in S,\ g_1g_2\gamma \in \Pi \}. \end{align} $$
Using the quantitative bounds in [Reference Green and TaoGT12b, Lemmas A.2 and A.3], we see that for each
![]() $\gamma \in \Gamma $
such that
$\gamma \in \Gamma $
such that
![]() $R_\gamma \neq \emptyset $
we have
$R_\gamma \neq \emptyset $
we have
![]() $|\widetilde \tau (\gamma )| = O(1/\delta ^{O(1)})$
. Hence, the union in (48) involves
$|\widetilde \tau (\gamma )| = O(1/\delta ^{O(1)})$
. Hence, the union in (48) involves
![]() $O(1/\delta ^{O(1)})$
non-empty terms, and in particular is finite. Each of the sets
$O(1/\delta ^{O(1)})$
non-empty terms, and in particular is finite. Each of the sets
![]() $R_\gamma $
is semialgebraic with complexity
$R_\gamma $
is semialgebraic with complexity
![]() $O(1)$
. Moreover, since
$O(1)$
. Moreover, since
![]() $\varepsilon '$
is a polynomial map of bounded degree, for each
$\varepsilon '$
is a polynomial map of bounded degree, for each
![]() $\gamma \in \Gamma $
the set
$\gamma \in \Gamma $
the set
is also semialgebraic with complexity
![]() $O(1)$
. Hence, (47) will follow once we show that for each semialgebraic set
$O(1)$
. Hence, (47) will follow once we show that for each semialgebraic set
![]() $T \subseteq [0,1) \times G/\Gamma $
with bounded complexity we have
$T \subseteq [0,1) \times G/\Gamma $
with bounded complexity we have

Following [Reference Green and TaoGT12a], we put
![]() $\widetilde{G}' := \gamma _j^{-1}G'\gamma _j$
,
$\widetilde{G}' := \gamma _j^{-1}G'\gamma _j$
,
![]() $\Lambda := \Gamma \cap \widetilde{G}'$
and
$\Lambda := \Gamma \cap \widetilde{G}'$
and
![]() $ \widetilde{g}'(n) := \gamma _j^{-1}g'(n)\gamma _j$
. Let also
$ \widetilde{g}'(n) := \gamma _j^{-1}g'(n)\gamma _j$
. Let also
![]() $D' = \dim G'$
, let
$D' = \dim G'$
, let
![]() $\sigma $
and
$\sigma $
and
![]() $\widetilde \sigma $
denote the coordinate maps on
$\widetilde \sigma $
denote the coordinate maps on
![]() $\widetilde{G}'/\Lambda $
and
$\widetilde{G}'/\Lambda $
and
![]() $\widetilde{G}'$
respectively, and let
$\widetilde{G}'$
respectively, and let
![]() $\Delta = \widetilde \sigma ^{-1}( [0,1)^{D'} )$
denote the fundamental domain. Then
$\Delta = \widetilde \sigma ^{-1}( [0,1)^{D'} )$
denote the fundamental domain. Then
![]() $\widetilde{g}'$
is a polynomial sequence with respect to the filtration
$\widetilde{g}'$
is a polynomial sequence with respect to the filtration
![]() $\widetilde{G}'_{\bullet }$
given by
$\widetilde{G}'_{\bullet }$
given by
![]() $\widetilde{G}'_{i} = \gamma _j^{-1}G^\prime _i\gamma _j$
. We have a well-defined map
$\widetilde{G}'_{i} = \gamma _j^{-1}G^\prime _i\gamma _j$
. We have a well-defined map
![]() $\iota \colon \widetilde{G}'/\Lambda \to G/\Gamma $
given by
$\iota \colon \widetilde{G}'/\Lambda \to G/\Gamma $
given by
Thus, for all
![]() $h \in [H]$
we have
$h \in [H]$
we have
As discussed in [Reference Green and TaoGT12b], the Lipschitz norm of the map
![]() $\iota $
is
$\iota $
is
![]() $O(M^{O(1)})$
and the sequence
$O(M^{O(1)})$
and the sequence
![]() $(\widetilde{G}'(h)\Lambda )_{h = 0}^{H-1}$
is
$(\widetilde{G}'(h)\Lambda )_{h = 0}^{H-1}$
is
![]() $1/M^{\unicode{x3bb} C+O(1)}$
-equidistributed, where
$1/M^{\unicode{x3bb} C+O(1)}$
-equidistributed, where
![]() $\unicode{x3bb}> 0$
is a constant dependent only on d and D.
$\unicode{x3bb}> 0$
is a constant dependent only on d and D.
For each
![]() $\gamma \in \Gamma $
, the map
$\gamma \in \Gamma $
, the map
![]() $\iota $
is a polynomial on the semialgebraic set
$\iota $
is a polynomial on the semialgebraic set
![]() $\Delta \cap \iota ^{-1}(\Pi \gamma )$
. The estimate on the Lipschitz norm of
$\Delta \cap \iota ^{-1}(\Pi \gamma )$
. The estimate on the Lipschitz norm of
![]() $\iota $
implies that
$\iota $
implies that
![]() $\Delta $
can be partitioned into
$\Delta $
can be partitioned into
![]() $M^{O(1)}$
semialgebraic sets with complexity
$M^{O(1)}$
semialgebraic sets with complexity
![]() $O(1)$
such that on each of the pieces
$O(1)$
such that on each of the pieces
![]() $\iota $
is a polynomial of degree
$\iota $
is a polynomial of degree
![]() $O(1)$
(using the coordinates
$O(1)$
(using the coordinates
![]() $\widetilde \tau $
and
$\widetilde \tau $
and
![]() $\widetilde \sigma $
). Applying the corresponding partition in (49), we see that it will suffice to show that for each semialgebraic set
$\widetilde \sigma $
). Applying the corresponding partition in (49), we see that it will suffice to show that for each semialgebraic set
![]() $T \subseteq (\mathbb {R}/\mathbb {Z}) \times (\widetilde{G}'/\Lambda )$
with bounded complexity and for each constant
$T \subseteq (\mathbb {R}/\mathbb {Z}) \times (\widetilde{G}'/\Lambda )$
with bounded complexity and for each constant
![]() $A'> 0$
we have
$A'> 0$
we have

Bearing in mind that
![]() $M \geq \log N$
, it will suffice to show that
$M \geq \log N$
, it will suffice to show that

We are now in position to apply Proposition 5.6 on
![]() $\widetilde{G}'/\Lambda $
. The complexity of
$\widetilde{G}'/\Lambda $
. The complexity of
![]() $(\widetilde{G}',\Lambda ,\widetilde{G}'_\bullet )$
is
$(\widetilde{G}',\Lambda ,\widetilde{G}'_\bullet )$
is
![]() $1/\delta '$
, where
$1/\delta '$
, where
![]() $\delta ' = 1/M^{O(1)}$
. The largest exponent
$\delta ' = 1/M^{O(1)}$
. The largest exponent
![]() $A'$
with which Proposition 5.6 is applicable to
$A'$
with which Proposition 5.6 is applicable to
![]() $(\widetilde{g}'(h))_{h=0}^{H-1}$
satisfies
$(\widetilde{g}'(h))_{h=0}^{H-1}$
satisfies
![]() $\log ^{A'}N \gg M^{\mu C}$
for a constant
$\log ^{A'}N \gg M^{\mu C}$
for a constant
![]() $\mu \gg 1$
, leading to
$\mu \gg 1$
, leading to

In order to derive (51) it is enough to let C be a sufficiently large multiple of A.
Acknowledgements
The authors wish to thank Michael Drmota for many insightful discussions, for suggesting this problem, and also for inviting the first-named author to Vienna for a visit during which this project started; and Fernando Xuancheng Shao for helpful comments on Möbius orthogonality of nilsequences. The authors are also grateful to the anonymous referee for careful reading of the paper and for thoughtful corrections.
During the initial work on this paper, the first-named author worked within the framework of the LABEX MILYON (ANR-10-LABX-0070) of Université de Lyon, within the ‘Investissements d’Avenir’ programme (ANR-11-IDEX-0007) operated by the French National Research Agency (ANR). Currently, he works at the University of Oxford and is supported by UKRI Fellowship EP/X033813/1. The second-named author is supported by the Austrian-French project ‘Arithmetic Randomness’ between FWF and ANR (grant numbers I4945-N and ANR-20-CE91-0006).
For the purpose of open access, the authors have applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising.