Multistate monotone systems are used to describe technological or biological systems when the system itself and its components can perform at different operationally meaningful levels. This generalizes the binary monotone systems used in standard reliability theory. In this paper we consider the availabilities and unavailabilities of the system in an interval, i.e. the probabilities that the system performs above or below the different levels throughout the whole interval. In complex systems it is often impossible to calculate these availabilities and unavailabilities exactly, but it is possible to construct lower and upper bounds based on the minimal path and cut vectors to the different levels. In this paper we consider systems which allow a modular decomposition. We analyse in depth the relationship between the minimal path and cut vectors for the system, the modules, and the organizing structure. We analyse the extent to which the availability bounds are improved by taking advantage of the modular decomposition. This problem was also treated in Butler (1982) and Funnemark and Natvig (1985), but the treatment was based on an inadequate analysis of the relationship between the different minimal path and cut vectors involved, and as a result was somewhat inaccurate. We also extend to interval bounds that have previously only been given for availabilities at a fixed point of time.

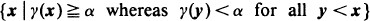A continuum structure function γ is a non-decreasing mapping from the unit hypercube to the unit interval. Block and Savits (1984) use the sets and 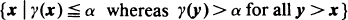to determine bounds on the distribution of γ (X) when X is a vector of associated random variables. It is shown that, if γ admits of a modular decomposition, improved bounds may be obtained.

A continuum structure function γ is a non-decreasing mapping from the unit hypercube to the unit interval. Minimal path (cut) sets of upper (lower) simple continuum structure functions are introduced and are used to determine bounds on the distribution of γ (Χ) when X is a vector of associated random variables and when γ is right (left)-continuous. It is shown that, if γ admits of a modular decomposition, improved bounds may be obtained.