Article contents
Bounding the stochastic performance of continuum structure functions. II
Published online by Cambridge University Press: 14 July 2016
Abstract
A continuum structure function γ is a non-decreasing mapping from the unit hypercube to the unit interval. Block and Savits (1984) use the sets 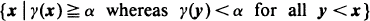 and
and 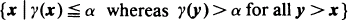 to determine bounds on the distribution of γ (X) when X is a vector of associated random variables. It is shown that, if γ admits of a modular decomposition, improved bounds may be obtained.
to determine bounds on the distribution of γ (X) when X is a vector of associated random variables. It is shown that, if γ admits of a modular decomposition, improved bounds may be obtained.
Information
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1987
Footnotes
Present address: Agency for Defense Development, P.O. Box 35, Daejeon, Korea.
Research supported by the National Science Foundation under grant ECS-8306871 and by the Air Force Office of Scientific Research, AFSC, USAF, under grant AFOSR-84-0243. The US Government is authorised to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright notation thereon.
References
- 10
- Cited by

