In a random sample of n pairs (Xr, Yr), r = 1, 2, …, n, drawn from a bivariate normal 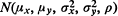 distribution, let Xr:n be the rth order statistic among the Xr and let Y[r:n] be the Y-variate paired with Xr:n. The Y[r:n], which we call concomitants of the order statistics, arise most naturally in selection procedures based on the Xr:n. It is shown that asymptotically the k quantities
distribution, let Xr:n be the rth order statistic among the Xr and let Y[r:n] be the Y-variate paired with Xr:n. The Y[r:n], which we call concomitants of the order statistics, arise most naturally in selection procedures based on the Xr:n. It is shown that asymptotically the k quantities 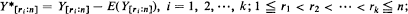 k fixed, are independent, identically distributed
k fixed, are independent, identically distributed 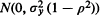 variates. In addition, putting Rt,n for the number of integers j for which
variates. In addition, putting Rt,n for the number of integers j for which 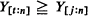 , the asymptotic distribution and all moments of n–1Rt, n are determined for t such that t/n → λ with 0 < λ < 1.
, the asymptotic distribution and all moments of n–1Rt, n are determined for t such that t/n → λ with 0 < λ < 1.

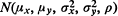 distribution, let
distribution, let 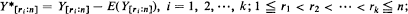
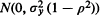 variates. In addition, putting
variates. In addition, putting 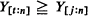 , the asymptotic distribution and all moments of
, the asymptotic distribution and all moments of 