Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T06:19:32.610Z Has data issue: false hasContentIssue false
  • English
  • Français

The asymptotic theory of concomitants of order statistics

Published online by Cambridge University Press:  14 July 2016

H. A. David  and
J. Galambos
H. A. David
Affiliation:
Iowa State University, Ames
J. Galambos*
Affiliation:
Iowa State University, Ames
*
*Now at Temple University, Philadelphia.
Get access Rights & Permissions [Opens in a new window]

Abstract

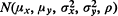In a random sample of n pairs (Xr, Yr), r = 1, 2, …, n, drawn from a bivariate normal distribution, let Xr:n be the rth order statistic among the Xr and let Y[r:n] be the Y-variate paired with Xr:n. The Y[r:n], which we call concomitants of the order statistics, arise most naturally in selection procedures based on the Xr:n. It is shown that asymptotically the k quantities 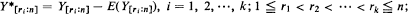k fixed, are independent, identically distributed 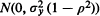variates. In addition, putting Rt,n for the number of integers j for which 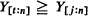, the asymptotic distribution and all moments of n–1Rt, n are determined for t such that t/n → λ with 0 < λ < 1.

Keywords

BIVARIATE NORMALORDER STATISTICSCONCOMITANTSSELECTIONSRANKASYMPTOTIC DISTRIBUTIONSMOMENTSMULTIVARIATE NORMAL
Type
Research Papers
Information
Journal of Applied Probability , Volume 11 , Issue 4 , December 1974 , pp. 762 - 770
Copyright
Copyright © Applied Probability Trust 1974 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Parts of this paper were presented by the first named author at the 39th Session of the I. S. I., Vienna, 1973. The present work was supported by the Army Research Office — Durham.

References

Anderson, T. W. (1958) Introduction to Multivariate Statistical Analysis. Wiley, New York.Google Scholar
Cramer, H. (1946) Mathematical Methods of Statistics. Princeton University Press, N. J.Google Scholar
Rao, C. R. (1965) Linear Statistical Inference and its Applications. Wiley, New York.Google Scholar
Watterson, G. A. (1959) Linear estimation in censored samples from multivariate normal populations. Ann. Math. Statist. 30, 814–824.Google Scholar