1 results
Improved Poisson approximations for word patterns
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 334-347
- Print publication:
- June 1993
-
- Article
- Export citation
-
Let X1, X2, · ··, Xn be a sequence of n random variables taking values in the ξ -letter alphabet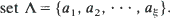
. We consider the number N = N(n, k) of non-overlapping occurrences of a fixed k-letter word under (a) i.i.d. and (b) stationary Markovian hypotheses on the sequence 
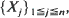, and use the Stein–Chen method to obtain Poisson approximations for the same. In each case, results and couplings from Barbour et al. (1992) are used to show that the total variation distance between the distribution of N and that of an appropriate Poisson random variable is of order (roughly) O(kS(k)), where S(k) denotes the stationary probability of the word in question. These results vastly improve on the approximations obtained in Godbole (1991). In the Markov case, we also make use of recently obtained eigenvalue bounds on convergence to stationarity due to Diaconis and Stroock (1991) and Fill (1991).
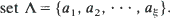. We consider the number 
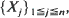, and use the Stein–Chen method to obtain Poisson approximations for the same. In each case, results and couplings from Barbour et al. (1992) are used to show that the total variation distance between the distribution of 