Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-11T06:53:27.903Z Has data issue: false hasContentIssue false
  • English
  • Français

Improved Poisson approximations for word patterns

Part of: Combinatorial probability Markov processes Limit theorems

Published online by Cambridge University Press:  01 July 2016

Anant P. Godbole  and
Andrew A. Schaffner
Anant P. Godbole*
Affiliation:
Michigan Technological University
Andrew A. Schaffner*
Affiliation:
California Polytechnic State University, San Luis Obispo
*
∗Postal address: Department of Mathematical Sciences, Michigan Technological University, Houghton, MI 49931, USA.
∗∗Postal address: Department of Mathematics, California Polytechnic State University, San Luis Obispo, CA 93407, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

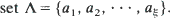Let X1, X2, · ··, Xn be a sequence of n random variables taking values in the ξ -letter alphabet . We consider the number N = N(n, k) of non-overlapping occurrences of a fixed k-letter word under (a) i.i.d. and (b) stationary Markovian hypotheses on the sequence 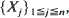, and use the Stein–Chen method to obtain Poisson approximations for the same. In each case, results and couplings from Barbour et al. (1992) are used to show that the total variation distance between the distribution of N and that of an appropriate Poisson random variable is of order (roughly) O(kS(k)), where S(k) denotes the stationary probability of the word in question. These results vastly improve on the approximations obtained in Godbole (1991). In the Markov case, we also make use of recently obtained eigenvalue bounds on convergence to stationarity due to Diaconis and Stroock (1991) and Fill (1991).

Keywords

NON-OVERLAPPING AND OVERLAPPING OCCURRENCES OF WORD PATTERNSPOISSON APPROXIMATIONSTEIN-CHEN METHODCOUPLINGRATES OF CONVERGENCE TO STATIONARITY

MSC classification

Primary: 60F05: Central limit and other weak theorems
Secondary: 60C05: Combinatorial probability 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Research Article
Information
Advances in Applied Probability , Volume 25 , Issue 2 , June 1993 , pp. 334 - 347
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of both authors was partially supported by U.S. National Science Foundation REU Grant DMS-9100829.

References

Arratia, R., Gordon, L. and Waterman, M. (1990) The Erdös–Rényi law in distribution, for coin tossing and sequence matching. Ann. Statist. 18, 539–570.Google Scholar
Barbour, A. D. and Eagleson, G. K. (1984) Poisson convergence for dissociated statistics. J. R. Statist. Soc. B 46, 397–402.Google Scholar
Barbour, A. D., Holst, L. and Janson, S. (1992) Poisson Approximation. Oxford University Press.Google Scholar
Chrysaphinou, O. and Papastavridis, S. (1988) A limit theorem on the number of overlapping appearances of a pattern in a sequence of independent trials. Prob. Theory Rel. Fields 79, 129–143.CrossRefGoogle Scholar
Chrysaphinou, O. and Papastavridis, S. (1990) The occurrence of sequence patterns in repeated dependent experiments. Theory Prob. Appl. 35, 145–152.Google Scholar
Diaconis, P. and Stroock, D. (1991) Geometric bounds for eigenvalues of Markov chains. Ann. Appl. Prob. 1, 36–61.Google Scholar
Fill, J. A. (1991) Eigenvalue bounds on convergence to stationarity for nonreversible Markov chains, with an application to the exclusion process. Ann. Appl. Prob. 1, 62–87.Google Scholar
Geske, M. X., Godbole, A. P. and Schaffner, A. A. (1992) Compound Poisson approximations for runs and patterns. Preprint.Google Scholar
Godbole, A. P. (1991) Poisson approximations for runs and patterns of rare events. Adv. Appl. Prob. 23, 851–865.CrossRefGoogle Scholar