We construct a family of compactifications of the affine cone of the Grassmannian variety of
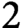 $2$
-planes. We show that both the tropical variety of the Plücker ideal and familiar valuations associated to the construction of Newton–Okounkov bodies for the Grassmannian variety can be recovered from these compactifications. In this way, we unite various perspectives for constructing toric degenerations of flag varieties.
$2$
-planes. We show that both the tropical variety of the Plücker ideal and familiar valuations associated to the construction of Newton–Okounkov bodies for the Grassmannian variety can be recovered from these compactifications. In this way, we unite various perspectives for constructing toric degenerations of flag varieties.