1 results
Dual ground state solutions for the critical nonlinear Helmholtz equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1155-1186
- Print publication:
- June 2020
-
- Article
- Export citation
-
Using a dual variational approach, we obtain nontrivial real-valued solutions of the critical nonlinear Helmholtz equation
for N ⩾ 4, where 2* : = 2N/(N − 2). The coefficient
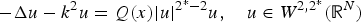$$-\Delta u-k^2u = Q(x) \vert u \vert ^{2^*-2}u,\quad u\in W^{2,2^*}({\open R}^{N})$$
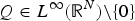$Q \in L^{\infty }({\open R}^{N}){\setminus }\{0\}$ is assumed to be nonnegative, asymptotically periodic and to satisfy a flatness condition at one of its maximum points. The solutions obtained are so-called dual ground states, that is, solutions arising from critical points of the dual functional with the property of having minimal energy among all nontrivial critical points. Moreover, we show that no dual ground state exists for N = 3.
