Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T04:29:45.679Z Has data issue: false hasContentIssue false
  • English
  • Français

Dual ground state solutions for the critical nonlinear Helmholtz equation

Part of: Elliptic equations and systems

Published online by Cambridge University Press:  30 January 2019

Gilles Evéquoz  and
Tolga Yeşil
Gilles Evéquoz
Affiliation:
Institut für Mathematik, Johann Wolfgang Goethe–Universität, Robert-Mayer-Str. 10, 60629 Frankfurt am Main, Germany (evequoz@math.uni-frankfurt.de; yesil@math.uni-frankfurt.de)
Tolga Yeşil
Affiliation:
Institut für Mathematik, Johann Wolfgang Goethe–Universität, Robert-Mayer-Str. 10, 60629 Frankfurt am Main, Germany (evequoz@math.uni-frankfurt.de; yesil@math.uni-frankfurt.de)
Get access Rights & Permissions [Opens in a new window]

Abstract

Using a dual variational approach, we obtain nontrivial real-valued solutions of the critical nonlinear Helmholtz equation

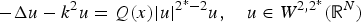$$-\Delta u-k^2u = Q(x) \vert u \vert ^{2^*-2}u,\quad u\in W^{2,2^*}({\open R}^{N})$$
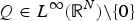for N ⩾ 4, where 2* : = 2N/(N − 2). The coefficient $Q \in L^{\infty }({\open R}^{N}){\setminus }\{0\}$ is assumed to be nonnegative, asymptotically periodic and to satisfy a flatness condition at one of its maximum points. The solutions obtained are so-called dual ground states, that is, solutions arising from critical points of the dual functional with the property of having minimal energy among all nontrivial critical points. Moreover, we show that no dual ground state exists for N = 3.

Keywords

Nonlinear Helmholtz equationcritical exponentdual variational methodnonvanishingnonexistence results

MSC classification

Primary: 35J20: Variational methods for second-order elliptic equations
Secondary: 35J05: Laplacian operator, reduced wave equation (Helmholtz equation), Poisson equation
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 3 , June 2020 , pp. 1155 - 1186
Copyright
Copyright © 2019 The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

Present address: School of Engineering, University of Applied Sciences of Western Switzerland, Route du Rawil 47, 1950 Sion, Switzerland (gilles.evequoz@hevs.ch)

References

1Ambrosetti, A. and Rabinowitz, P. H.. Dual variational methods in critical point theory and applications. J. Funct. Anal. 14 (1973), 349–381.10.1016/0022-1236(73)90051-7CrossRefGoogle Scholar
2Ambrosetti, A. and Struwe, M.. A note on the problem $-\Delta u=\lambda u+u\vert u\vert ^{2^{\ast }}-2$. Man. Math. 54 (1986), 373–379.10.1007/BF01168482CrossRefGoogle Scholar
3Brézis, H. and Nirenberg, L.. Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents. Comm. Pure Appl. Math. 36 (1983), 437–477.CrossRefGoogle Scholar
4Chabrowski, J. and Szulkin, A.. On a semilinear Schrödinger equation with critical Sobolev exponent. Proc. Amer. Math. Soc. 130 (2002), 85–93 (electronic).10.1090/S0002-9939-01-06143-3CrossRefGoogle Scholar
5Dolbeault, J.. Sobolev and Hardy–Littlewood–Sobolev inequalities: duality and fast diffusion. Math. Res. Lett. 18 (2011), 1037–1050.CrossRefGoogle Scholar
6Egnell, H.. Semilinear elliptic equations involving critical Sobolev exponents. Arch. Ration. Mech. Anal. 104 (1988), 27–56.10.1007/BF00256931CrossRefGoogle Scholar
7Escobar, J. F.. Positive solutions for some semilinear elliptic equations with critical Sobolev exponents. Comm. Pure Appl. Math. 40 (1987), 623–657.CrossRefGoogle Scholar
8Evéquoz, G.. Multiple standing waves for the nonlinear Helmholtz equation concentrating in the high frequency limit. Ann. Mat. Pura Appl. 196 (2017a), 2023–2042.10.1007/s10231-017-0651-6CrossRefGoogle Scholar
9Evéquoz, G.. On the periodic and asymptotically periodic nonlinear Helmholtz equation. Nonlin. Anal. 152 (2017b), 88–101.10.1016/j.na.2016.12.012CrossRefGoogle Scholar
10Evéquoz, G. and Weth, T.. Real solutions to the nonlinear Helmholtz equation with local nonlinearity. Arch. Ration. Mech. Anal. 211 (2014), 359–388.CrossRefGoogle Scholar
11Evéquoz, G. and Weth, T.. Dual variational methods and nonvanishing for the nonlinear Helmholtz equation. Adv. Math. 280 (2015), 690–728.10.1016/j.aim.2015.04.017CrossRefGoogle Scholar
12Gelfand, I. M. and Shilov, G. E.. Generalized functions, vol. 1, properties and operations (Amsterdam: Academic Press, 1964).Google Scholar
13Kato, T.. Growth properties of solutions of the reduced wave equation with a variable coefficient. Comm. Pure Appl. Math. 12 (1959), 403–425.10.1002/cpa.3160120302CrossRefGoogle Scholar
14Kenig, C. E., Ruiz, A. and Sogge, C.. Uniform Sobolev inequalities and unique continuation for second order constant coefficient differential operators. Duke Math. J. 55 (1987), 329–347.10.1215/S0012-7094-87-05518-9CrossRefGoogle Scholar
15Lebedev, N. N.. Special functions and their applications, Revised edn (translated from the Russian and edited by R. A. Silverman) (New York: Dover, 2012).Google Scholar
16Lieb, E. H.. Sharp constants in the Hardy–Littlewood–Sobolev and related inequalities. Ann. of Math. 118 (1983), 349–374.CrossRefGoogle Scholar
17Lieb, E. H. and Loss, M.. Analysis, 2nd edn, Graduate Studies in Mathematics, vol. 14 (Providence: American Mathematical Society, 2001).Google Scholar
18Lions, P.-L.. The concentration-compactness principle in the calculus of variations. The locally compact case. I, II. Ann. Inst. H. Poincaré Anal. Non Linéaire 1 (1984), 109–145, 223–283.10.1016/S0294-1449(16)30428-0CrossRefGoogle Scholar
19Mandel, R., Montefusco, E. and Pellacci, B.. Oscillating solutions for nonlinear Helmholtz equations. Z. Angew. Math. Phys. 68 (2017), 19.10.1007/s00033-017-0859-8CrossRefGoogle Scholar
20Rellich, F.. Über das asymptotische Verhalten der Lösungen von Δu + λu = 0 in unendlichen Gebieten. Jber. Deutsch. Math. Verein. 53 (1943), 57–65.Google Scholar
21Rudin, W.. Functional analysis, 2nd edn, International Series in Pure and Applied Mathematics (New York: McGraw-Hill, 1991).Google Scholar
22Willem, M.. Minimax theorems. Progress in nonlinear differential equations and their applications, vol. 24 (Boston: Birkhäuser, 1996).CrossRefGoogle Scholar