We study existence and approximation of non-negative solutions of partial differential equations of the type 
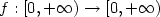 $$\partial_t u - \div (A(\nabla (f(u))+u\nabla V )) = 0 \qquad \mbox{in } (0,+\infty )\times \mathbb{R}^n,\qquad\qquad (0.1)$$ where A is a symmetric matrix-valued function of the spatial variable satisfying a uniform ellipticity condition, $f:[0,+\infty) \rightarrow[0,+\infty)$ is a suitable non decreasing function, $V:\mathbb{R}^n \rightarrow\mathbb{R}$ 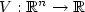is a convex function.Introducing the energy functional $\phi(u)=\int_{\mathbb{R}^n} F(u(x))\,{\rm d}x+\int_{\mathbb{R}^n}V(x)u(x)\,{\rm d}x$ 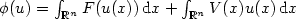,where F is a convex function linked to f by $f(u) = uF'(u)-F(u)$ 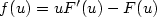,we show that u is the “gradient flow” of ϕ with respect to the2-Wasserstein distance between probability measures onthe space $\mathbb{R}^n$ 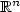, endowed with the Riemannian distance induced by $A^{-1}.$ 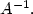In the case of uniform convexity of V, long time asymptotic behaviour and decay rate to the stationary statefor solutions of equation (0.1) are studied.A contraction property in Wasserstein distance for solutions of equation (0.1)is also studied in a particular case.

In this article, we consider the initial value problem which is obtained after a space discretization (with space step h) of the equations governing the solidification process of a multicomponent alloy. We propose a numerical scheme to solve numerically this initial value problem. We prove an error estimate which is not affected by the step size h chosen in the space discretization. Consequently, our scheme provides global convergence without any stability condition between h and the time step size τ. Moreover, it is not of excessive algorithmic complexity since it does not require more than one resolution of a linear system at each time step.