Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bolley, François
Gentil, Ivan
and
Guillin, Arnaud
2012.
Convergence to equilibrium in Wasserstein distance for Fokker–Planck equations.
Journal of Functional Analysis,
Vol. 263,
Issue. 8,
p.
2430.
Bolley, François
Gentil, Ivan
and
Guillin, Arnaud
2013.
Uniform Convergence to Equilibrium for Granular Media.
Archive for Rational Mechanics and Analysis,
Vol. 208,
Issue. 2,
p.
429.
Liero, Matthias
and
Mielke, Alexander
2013.
Gradient structures and geodesic convexity for reaction–diffusion systems.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 371,
Issue. 2005,
p.
20120346.
Wu, Lijiang
and
Slepčev, Dejan
2015.
Nonlocal Interaction Equations in Environments with Heterogeneities and Boundaries.
Communications in Partial Differential Equations,
Vol. 40,
Issue. 7,
p.
1241.
Cancès, Clément
Gallouët, Thomas O.
and
Monsaingeon, Léonard
2015.
The gradient flow structure for incompressible immiscible two-phase flows in porous media.
Comptes Rendus. Mathématique,
Vol. 353,
Issue. 11,
p.
985.
Fathi, Max
2016.
A gradient flow approach to large deviations for diffusion processes.
Journal de Mathématiques Pures et Appliquées,
Vol. 106,
Issue. 5,
p.
957.
Mimura, Yoshifumi
2017.
The variational formulation of the fully parabolic Keller–Segel system with degenerate diffusion.
Journal of Differential Equations,
Vol. 263,
Issue. 2,
p.
1477.
Cancès, Clément
and
Guichard, Cindy
2017.
Numerical Analysis of a Robust Free Energy Diminishing Finite Volume Scheme for Parabolic Equations with Gradient Structure.
Foundations of Computational Mathematics,
Vol. 17,
Issue. 6,
p.
1525.
Cancès, Clément
Gallouët, Thomas O.
and
Monsaingeon, Léonard
2017.
Incompressible immiscible multiphase flows in porous media: a variational approach.
Analysis & PDE,
Vol. 10,
Issue. 8,
p.
1845.
Bolley, François
Gentil, Ivan
and
Guillin, Arnaud
2018.
Dimensional improvements of the logarithmic Sobolev, Talagrand and Brascamp–Lieb inequalities.
The Annals of Probability,
Vol. 46,
Issue. 1,
Ferreira, Lucas C. F.
and
Valencia-Guevara, Julio C.
2018.
Gradient flows of time-dependent functionals in metric spaces and applications to PDEs.
Monatshefte für Mathematik,
Vol. 185,
Issue. 2,
p.
231.
Wei, Susan
and
Panaretos, Victor M.
2018.
Empirical evolution equations.
Electronic Journal of Statistics,
Vol. 12,
Issue. 1,
CANCÈS, CLÉMENT
GALLOUËT, THOMAS
LABORDE, MAXIME
and
MONSAINGEON, LÉONARD
2019.
Simulation of multiphase porous media flows with minimising movement and finite volume schemes.
European Journal of Applied Mathematics,
Vol. 30,
Issue. 6,
p.
1123.
Zinsl, Jonathan
2019.
Well-posedness of evolution equations with time-dependent nonlinear mobility: A modified minimizing movement scheme.
Advances in Calculus of Variations,
Vol. 12,
Issue. 4,
p.
423.
Carrillo, José A.
Choi, Young-Pil
and
Tse, Oliver
2019.
Convergence to Equilibrium in Wasserstein Distance for Damped Euler Equations with Interaction Forces.
Communications in Mathematical Physics,
Vol. 365,
Issue. 1,
p.
329.
Garbuno-Inigo, Alfredo
Nüsken, Nikolas
and
Reich, Sebastian
2020.
Affine Invariant Interacting Langevin Dynamics for Bayesian Inference.
SIAM Journal on Applied Dynamical Systems,
Vol. 19,
Issue. 3,
p.
1633.
Halder, Abhishek
Caluya, Kenneth F.
Travacca, Bertrand
and
Moura, Scott J.
2020.
Hopfield Neural Network Flow: A Geometric Viewpoint.
IEEE Transactions on Neural Networks and Learning Systems,
Vol. 31,
Issue. 11,
p.
4869.
Li, Buyang
Ueda, Yuki
and
Zhou, Guanyu
2020.
A Second-Order Stabilization Method for Linearizing and Decoupling Nonlinear Parabolic Systems.
SIAM Journal on Numerical Analysis,
Vol. 58,
Issue. 5,
p.
2736.
Fetecau, Razvan C.
Park, Hansol
and
Patacchini, Francesco S.
2021.
Well-posedness and asymptotic behavior of an aggregation model with intrinsic interactions on sphere and other manifolds.
Analysis and Applications,
Vol. 19,
Issue. 06,
p.
965.
Chalub, Fabio A. C. C.
Monsaingeon, Léonard
Ribeiro, Ana Margarida
and
Souza, Max O.
2021.
Gradient Flow Formulations of Discrete and Continuous Evolutionary Models: A Unifying Perspective.
Acta Applicandae Mathematicae,
Vol. 171,
Issue. 1,
 where A is a symmetric matrix-valued function of the spatial variable satisfying a uniform ellipticity condition, $f:[0,+\infty) \rightarrow[0,+\infty)$
where A is a symmetric matrix-valued function of the spatial variable satisfying a uniform ellipticity condition, $f:[0,+\infty) \rightarrow[0,+\infty)$ 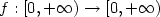 is a suitable non decreasing function, $V:\mathbb{R}^n \rightarrow\mathbb{R}$
is a suitable non decreasing function, $V:\mathbb{R}^n \rightarrow\mathbb{R}$ 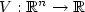 is a convex function.Introducing the energy functional $\phi(u)=\int_{\mathbb{R}^n} F(u(x))\,{\rm d}x+\int_{\mathbb{R}^n}V(x)u(x)\,{\rm d}x$
is a convex function.Introducing the energy functional $\phi(u)=\int_{\mathbb{R}^n} F(u(x))\,{\rm d}x+\int_{\mathbb{R}^n}V(x)u(x)\,{\rm d}x$ 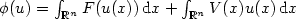 ,where F is a convex function linked to f by $f(u) = uF'(u)-F(u)$
,where F is a convex function linked to f by $f(u) = uF'(u)-F(u)$ 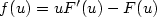 ,we show that u is the “gradient flow” of ϕ with respect to the2-Wasserstein distance between probability measures onthe space $\mathbb{R}^n$
,we show that u is the “gradient flow” of ϕ with respect to the2-Wasserstein distance between probability measures onthe space $\mathbb{R}^n$ 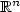 , endowed with the Riemannian distance induced by $A^{-1}.$
, endowed with the Riemannian distance induced by $A^{-1}.$ 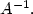 In the case of uniform convexity of V, long time asymptotic behaviour and decay rate to the stationary statefor solutions of equation (0.1) are studied.A contraction property in Wasserstein distance for solutions of equation (0.1)is also studied in a particular case.
In the case of uniform convexity of V, long time asymptotic behaviour and decay rate to the stationary statefor solutions of equation (0.1) are studied.A contraction property in Wasserstein distance for solutions of equation (0.1)is also studied in a particular case.
