PageRank is a ranking method that assigns scores to web pages using the limit
distribution of a random walk on the web graph. A fibration of graphs is a
morphism that is a local isomorphism of in-neighbourhoods, much in the same way
a covering projection is a local isomorphism of neighbourhoods. We show that a
deep connection relates fibrations and Markov chains with restart, a
particular kind of Markov chains that include the PageRank one as a
special case. This fact provides constraints on the values that PageRank can
assume. Using our results, we show that a recently defined class of graphs that
admit a polynomial-time isomorphism algorithm based on the computation of
PageRank is really a subclass of fibration-prime graphs, which possess
simple, entirely discrete polynomial-time isomorphism algorithms based on
classical techniques for graph isomorphism. We discuss efficiency issues in the
implementation of such algorithms for the particular case of web graphs, in which
O(n) space occupancy (where n is the number of nodes) may be acceptable, but
O(m) is not (where m is the number of arcs).


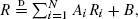 where the
where the 