Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T13:58:24.591Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic analysis for personalized Web search

Part of: Theory of data Operations research and management science Inversion theorems

Published online by Cambridge University Press:  01 July 2016

Yana Volkovich  and
Nelly Litvak
Yana Volkovich*
Affiliation:
University of Twente
Nelly Litvak*
Affiliation:
University of Twente
*
∗ Current address: Barcelona Media - Innovation Center, Av. Diagonal 177, 9th Floor, 08018 Barcelona, Spain. Email address: yana.volkovich@barcelonamedia.org
∗∗ Postal address: Faculty of EEMCS, University of Twente, 7500 AE Enschede, The Netherlands. Email address: n.litvak@ewi.utwente.nl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

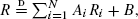PageRank with personalization is used in Web search as an importance measure for Web documents. The goal of this paper is to characterize the tail behavior of the PageRank distribution in the Web and other complex networks characterized by power laws. To this end, we model the PageRank as a solution of a stochastic equation where the Ris are distributed as R. This equation is inspired by the original definition of the PageRank. In particular, N models the number of incoming links to a page, and B stays for the user preference. Assuming that N or B are heavy tailed, we employ the theory of regular variation to obtain the asymptotic behavior of R under quite general assumptions on the involved random variables. Our theoretical predictions show good agreement with experimental data.

Keywords

PageRankWebregular variationstochastic equationTauberian theorem

MSC classification

Primary: 68P10: Searching and sorting 90B15: Network models, stochastic
Secondary: 40E05: Tauberian theorems, general
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 42 , Issue 2 , June 2010 , pp. 577 - 604
Copyright
Copyright © Applied Probability Trust 2010 

References

Andersen, R., Chung, F. and Lang, K. (2006). Local graph partitioning using PageRank vectors. In Proc. FOCS 2006, IEEE Computer Society, Washington, DC, pp. 475–486.Google Scholar
Andersen, R., Chung, F. and Lang, K. (2007). Local partitioning for directed graphs using PageRank. In Algorithms and Models for the Web-Graph (Lecture Notes Comput. Sci. 4863), Springer, Berlin, pp. 166–178.CrossRefGoogle Scholar
Avrachenkov, K. and Lebedev, D. (2006). PageRank of scale-free growing networks. Internet Math. 3, 207–231.CrossRefGoogle Scholar
Avrachenkov, K., Litvak, N. and Pham, K. S. (2007). Distribution of PageRank mass among principle components of the web. In Algorithms and Models for the Web-Graph (Lecture Notes Comput. Sci. 4863), Springer, Berlin, pp. 16–28.CrossRefGoogle Scholar
Barabási, A.-L. and Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509–512.CrossRefGoogle ScholarPubMed
Bingham, N. H., Goldie, C. M. and Teugels, J. L. (1989). Regular Variation. Cambridge University Press.Google Scholar
Boldi, P., Santini, M. and Vigna, S. (2005). PageRank as a function of the damping factor. In Proc. 14th Internat. Conf. World Wide Web, ACM, New York, pp. 557–566.Google Scholar
Brin, S. and Page, L. (1998). The anatomy of a large-scale hypertextual Web search engine. Comput. Networks ISDN Systems 30, 107–117.CrossRefGoogle Scholar
Broder, A. et al. (2000). Graph structure in the Web. Comput. Networks 33, 309–320.CrossRefGoogle Scholar
Chen, P., Xie, H., Maslov, S. and Redner, S. (2007). Finding scientific gems with Google's PageRank algorithm. J. Informetrics 1, 8–15.CrossRefGoogle Scholar
Constantine, P. G. and Gleich, D. F. (2007). Using polynomial chaos to compute the influence of multiple random surfers in the PageRank model. In Algorithms and Models for the Web-Graph (Lecture Notes Comput. Sci. 4863), Springer, Berlin, pp. 82–95.CrossRefGoogle Scholar
De Meyer, A. and Teugels, J. L. (1980). On the asymptotic behaviour of the distributions of the busy period and service time in M/G/1. J. Appl. Prob. 17, 802–813.CrossRefGoogle Scholar
Fortunato, S. and Flammini, A. (2007). Random walks on directed networks: the case of PageRank. Internat. J. Bifur. Chaos Appl. Sci. Eng. 17, 2343–2353.CrossRefGoogle Scholar
Fortunato, S., Boguñá, M., Flammini, A. and Menczer, F. (2006). Approximating PageRank from in-degree. In Algorithms and Models for the Web-Graph (Lecture Notes Comput. Sci. 4936), Springer, Berlin, pp. 59–71.Google Scholar
Gyöngyi, Z., Garcia-Molina, H. and Pedersen, J. (2004). Combating Web spam with TrustRank. In Proc. 13th Internat. Conf. Very Large Data Bases, VLDB Endowment, pp. 576–587.Google Scholar
Haveliwala, T. H. (2003). Topic-sensitive PageRank: a context-sensitive ranking algorithm for Web search. IEEE Trans. Knowledge Data Eng. 15, 784–796.CrossRefGoogle Scholar
Haveliwala, T. H., Kamvar, A. and Jeh, G. (2003). An analytical comparison of approaches to personalizing PageRank. Tech. Rep., Stanford University.Google Scholar
Jeh, G. and Widom, J. (2003). Scaling personalized Web search. In Proc. 12th Internat. Conf. World Wide Web, ACM, New York, pp. 271–279.Google Scholar
Jelenkovic, P. R. and Olvera-Cravioto, M. (2009). Information ranking and power laws on trees. Preprint. Available at http://arxiv.org/abs/0905.1738.Google Scholar
Jessen, A. H. and Mikosch, T. (2006). Regularly varying functions. Publ. Inst. Math. (Beograd) (N.S.) 80, 171–192.CrossRefGoogle Scholar
Kamvar, S. D., Haveliwala, T. H., Manning, C. D. and Golub, G. H. (2003). Exploiting the block structure of the Web for computing. Tech. Rep., Stanford University.Google Scholar
Kleinberg, J. M. (1999). Authoritative sources in a hyperlinked environment. J. ACM 46, 604–632.CrossRefGoogle Scholar
Kraaij, W., Westerveld, T. and Hiemstra, D. (2002). The importance of prior probabilities for entry page search. In Proc. 25th Annual Internat. ACM SIGIR Conf. Research and Development in Information Retrieval, ACM, New York, pp. 27–34.Google Scholar
Langville, A. N. and Meyer, C. D. (2006). Google's PageRank and Beyond: the Science of Search Engine Rankings. Princeton University Press.CrossRefGoogle Scholar
Leskovec, J. and Faloutsos, C. (2006). Sampling from large graphs. In Proc. 12th ACM SIGKDD Internat. Conf. Knowledge Discovery and Data Mining, ACM, New York, pp. 631–636.Google Scholar
Litvak, N., Scheinhardt, W. R. W. and Volkovich, Y. (2007). In-degree and PageRank: why do they follow similar power laws? Internet Math. 4, 175–198.CrossRefGoogle Scholar
Litvak, N., Scheinhardt, W., Volkovich, Y. and Zwart, B. (2009). Characterization of tail dependence for in-degree and PageRank. In Algorithms and Models for the Web-Graph (Lecture Notes Comput. Sci. 5427), Springer, Berlin, pp. 90–103.CrossRefGoogle Scholar
Liu, Q. (1998). Fixed points of a generalized smoothing transformation and applications to the branching random walk. Adv. Appl. Prob. 30, 85–112.CrossRefGoogle Scholar
Liu, Q. (2001). Asymptotic properties and absolute continuity of laws stable by random weighted mean. Stoch. Process. Appl. 95, 83–107.CrossRefGoogle Scholar
Micarelli, A., Gasparetti, F., Sciarrone, F. and Gauch, S. (2007). Personalized search on the World Wide Web. In The Adaptive Web (Lecture Notes Comput. Sci. 4321), Springer, Berlin, pp. 195–230.CrossRefGoogle Scholar
Page, L., Brin, S., Motwani, R. and Winograd, T. (1998). The PageRank citation ranking: bringing order to the Web. Tech. Rep., Stanford Digital Library Technologies Project.Google Scholar
Pandurangan, G., Raghavan, P. and Upfal, E. (2002). Using PageRank to characterize Web structure. In Computing and Combinatorics (Lecture Notes Comput. Sci. 2387), Springer, Berlin, pp. 330–339.CrossRefGoogle Scholar
Ponte, J. M. and Croft, W. B. (1998). A language modeling approach to information retrieval. In Proc. 21st Annual Internat. ACM SIGIR Conf. Research and Development in Information Retrieval. ACM, New York, pp. 275–281.Google Scholar
Resnick, S. I. (2007). Heavy-tail Phenomena. Springer, New York.Google Scholar
Richardson, M. and Domingos, P. (2002). The intelligent surfer: probabilistic combination of link and content information in PageRank. Adv. NIPS 14, 1441–1448.Google Scholar
Ross, S. M. (2003). The inspection paradox. Prob. Eng. Inform. Sci. 17, 47–51.CrossRefGoogle Scholar
Volkovich, Y., Litvak, N. and Donato, D. (2007). Determining factors behind the PageRank log-log plot. In Algorithms and Models for the Web-Graph (Lecture Notes Comput. Sci. 4863), Springer, Berlin, pp. 108–123.CrossRefGoogle Scholar
Volkovich, Y., Litvak, N. and Zwart, B. (2008). A framework for evaluating statistical dependencies and rank correlations in power law graphs. Memorandum 1868. University of Twente Enschede.Google Scholar
Volkovich, Y., Litvak, N. and Zwart, B. (2009). Extremal dependencies and rank correlations in power law networks. In Complex Sciences, Springer, Berlin, pp. 1642–1653.CrossRefGoogle Scholar
Zwart, A. P. (2001). Queueing systems with heavy tails. , Eindhoven University of Technology.Google Scholar