The curse of dimensionality confounds the comprehensive evaluation of computational structural mechanics problems. Adequately capturing complex material behavior and interacting physics phenomenon in models can lead to long run times and memory requirements resulting in the need for substantial computational resources to analyze one scenario for a single set of input parameters. The computational requirements are then compounded when considering the number and range of input parameters spanning material properties, loading, boundary conditions, and model geometry that must be evaluated to characterize behavior, identify dominant parameters, perform uncertainty quantification, and optimize performance. To reduce model dimensionality, global sensitivity analysis (GSA) enables the identification of dominant input parameters for a specific structural performance output. However, many distinct types of GSA methods are available, presenting a challenge when selecting the optimal approach for a specific problem. While substantial documentation is available in the literature providing details on the methodology and derivation of GSA methods, application-based case studies focus on fields such as finance, chemistry, and environmental science. To inform the selection and implementation of a GSA method for structural mechanics problems for a nonexpert user, this article investigates five of the most widespread GSA methods with commonly used structural mechanics methods and models of varying dimensionality and complexity. It is concluded that all methods can identify the most dominant parameters, although with significantly different computational costs and quantitative capabilities. Therefore, method selection is dependent on computational resources, information required from the GSA, and available data.
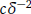 (where
(where 