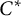 $C^*$
-algebras induced by equivalence bimodules
$C^*$
-algebras induced by equivalence bimodules
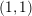 $(1,1)$ theorem
$(1,1)$ theorem
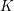 $K$-theory spectra at height
$K$-theory spectra at height 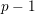 $p-1$
$p-1$
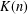 $K(n)$-LOCAL PICARD GROUP
$K(n)$-LOCAL PICARD GROUP