Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T08:38:09.746Z Has data issue: false hasContentIssue false
  • English
  • Français

The Picard groups of inclusions of 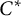$C^*$-algebras induced by equivalence bimodules

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  06 July 2021

Kazunori Kodaka
Kazunori Kodaka*
Affiliation:
Department of Mathematical Sciences, Faculty of Science, Ryukyu University, Nishihara-cho, Okinawa903-0213, Japan
*
e-mail: kodaka@math.u-ryukyu.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

For two 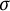$\sigma $ -unital 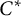$C^*$ -algebras, we consider two equivalence bimodules over them, respectively. Then, by taking the crossed products by the equivalence bimodules, we get two inclusions of 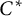$C^*$ -algebras. Furthermore, we suppose that one of the inclusions of 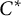$C^*$ -algebras is irreducible, that is, the relative commutant of one of the 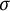$\sigma $ -unital 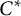$C^*$ -algebras in the multiplier 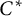$C^*$ -algebra of the crossed product is trivial. We will give a sufficient and necessary condition that the two inclusions are strongly Morita equivalent. Applying this result, we will compute the Picard group of a unital inclusion of unital 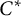$C^*$ -algebras induced by an equivalence bimodule over the unital 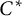$C^*$ -algebra under the assumption that the unital inclusion of unital 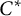$C^*$ -algebras is irreducible.

Keywords

Crossed productsequivalence bimodulesinclusions of C*-algebrasstrong Morita equivalencePicard groups

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 46L08: $C^*$-modules
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 3 , September 2022 , pp. 743 - 758
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abadie, B., Eilers, S., and Exel, R., Morita equivalence for crossed products by Hilbert C*-bimodules. Trans. Amer. Math. Soc. 350(1998), 3043–3054.CrossRefGoogle Scholar
Bédos, E. and Conti, R., On discrete twisted C*-dynamical systems, Hilbert C*-modules and regularity. Münster J. Math. 5(2012), 183–208.Google Scholar
Brown, L. G., Green, P., and Rieffel, M. A., Stable isomorphism and strong Morita equivalence of C*-algebras. Pacific J. Math. 71(1977), 349–363.CrossRefGoogle Scholar
Brown, L. G., Mingo, J., and Shen, N.-T., Quasi-multipliers and embeddings of Hilbert C*-bimodules. Canad. J. Math. 46(1994), 1150–1174.10.4153/CJM-1994-065-5CrossRefGoogle Scholar
Jensen, K. K. and Thomsen, K., Elements of KK-theory, Birkhuser Birkhäuser, 1991.10.1007/978-1-4612-0449-7CrossRefGoogle Scholar
Kodaka, K., The Picard groups for unital inclusions of unital C*-algebras. Acta Sci. Math. (Szeged) 86(2020), 183–207.CrossRefGoogle Scholar
Kodaka, K., Equivalence bundles over a finite group and strong Morita equivalence for unital inclusions of unital C*-algebras. Math. Bohem., to appear.Google Scholar
Kodaka, K., Strong Morita equivalence for inclusions of C*-algebras induced by twisted actions of a countable discrete group. Math. Scand., to appear.Google Scholar
Kodaka, K. and Teruya, T., Involutive equivalence bimodules and inclusions of C*-algebras with Watatani index 2. J. Operator Theory 57(2007), 3–18.Google Scholar
Kodaka, K. and Teruya, T., The strong Morita equivalence for inclusions of C*-algebras and conditional expectations for equivalence bimodules. J. Aust. Math. Soc. 105(2018), 103–144.CrossRefGoogle Scholar
Kodaka, K. and Teruya, T., Coactions of a finite dimensional C*-Hopf algebra on unital C*-algebras, unital inclusions of unital C*-algebras and the strong Morita equivalence. Studia Math. 256(2021), 147–167.CrossRefGoogle Scholar