Let 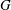it(G) be the number of independent sets of size t in a graph G. Engbers and Galvin asked how large it(G) could be in graphs with minimum degree at least δ. They further conjectured that when n ⩾ 2δ and t ⩾ 3, it(G) is maximized by the complete bipartite graph Kδ,n−δ. This conjecture has recently drawn the attention of many researchers. In this short note, we prove this conjecture.

Let $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}G$ be a graph and ${{\tau }}$ be an assignment of nonnegative thresholds to the vertices of 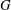$G$. A subset of vertices, 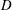$D$, is an irreversible dynamic monopoly of 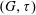$(G, \tau )$ if the vertices of 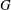$G$ can be partitioned into subsets 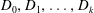$D_0, D_1, \ldots, D_k$ such that 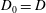$D_0=D$ and, for all 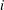$i$ with 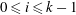$0 \leq i \leq k-1$, each vertex $v$ in 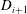$D_{i+1}$ has at least 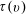$\tau (v)$ neighbours in the union of 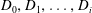$D_0, D_1, \ldots, D_i$. Dynamic monopolies model the spread of influence or propagation of opinion in social networks, where the graph 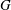$G$ represents the underlying network. The smallest cardinality of any dynamic monopoly of 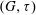$(G,\tau )$ is denoted by 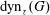$\mathrm{dyn}_{\tau }(G)$. In this paper we assume that the threshold of each vertex $v$ of the network is a random variable 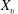$X_v$ such that 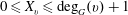$0\leq X_v \leq \deg _G(v)+1$. We obtain sharp bounds on the expectation and the concentration of 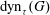$\mathrm{dyn}_{\tau }(G)$ around its mean value. We also obtain some lower bounds for the size of dynamic monopolies in terms of the order of graph and expectation of the thresholds.