Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T20:07:40.520Z Has data issue: false hasContentIssue false
  • English
  • Français

ON DYNAMIC MONOPOLIES OF GRAPHS WITH PROBABILISTIC THRESHOLDS

Part of: Mathematical sociology Graph theory

Published online by Cambridge University Press:  09 September 2014

HOSSEIN SOLTANI  and
MANOUCHEHR ZAKER
HOSSEIN SOLTANI
Affiliation:
Department of Mathematics, Institute for Advanced Studies in Basic Sciences, Zanjan 45137-66731, Iran email h_soltani@iasbs.ac.ir
MANOUCHEHR ZAKER*
Affiliation:
Department of Mathematics, Institute for Advanced Studies in Basic Sciences, Zanjan 45137-66731, Iran email mzaker@iasbs.ac.ir
*
✉mzaker@iasbs.ac.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 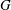$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}G$ be a graph and ${{\tau }}$ be an assignment of nonnegative thresholds to the vertices of 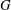$G$. A subset of vertices, 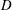$D$, is an irreversible dynamic monopoly of 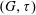$(G, \tau )$ if the vertices of 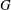$G$ can be partitioned into subsets 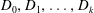$D_0, D_1, \ldots, D_k$ such that 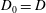$D_0=D$ and, for all 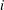$i$ with 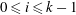$0 \leq i \leq k-1$, each vertex $v$ in 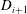$D_{i+1}$ has at least 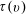$\tau (v)$ neighbours in the union of 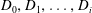$D_0, D_1, \ldots, D_i$. Dynamic monopolies model the spread of influence or propagation of opinion in social networks, where the graph 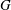$G$ represents the underlying network. The smallest cardinality of any dynamic monopoly of 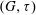$(G,\tau )$ is denoted by 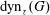$\mathrm{dyn}_{\tau }(G)$. In this paper we assume that the threshold of each vertex $v$ of the network is a random variable 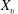$X_v$ such that 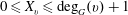$0\leq X_v \leq \deg _G(v)+1$. We obtain sharp bounds on the expectation and the concentration of 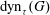$\mathrm{dyn}_{\tau }(G)$ around its mean value. We also obtain some lower bounds for the size of dynamic monopolies in terms of the order of graph and expectation of the thresholds.

Keywords

spread of influence in graphsirreversible dynamic monopoliesprobabilistic threshold assignment

MSC classification

Secondary: 05C69: Dominating sets, independent sets, cliques 91D30: Social networks
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 3 , December 2014 , pp. 363 - 375
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Ackerman, E., Ben-Zwi, O. and Wolfovitz, G., ‘Combinatorial model and bounds for target set selection’, Theoret. Comput. Sci. 411 (2010), 4017–4022.Google Scholar
Adams, S. S., Booth, P., Troxell, D. S. and Zinnen, S. L., ‘Modeling the spread of fault in majority-based network systems: dynamic monopolies in triangular grids’, Discrete Appl. Math. 160 (2012), 1624–1633.CrossRefGoogle Scholar
Balogh, J. and Bollobás, B., ‘Bootstrap percolation on the hypercube’, Probab. Theory Related Fields 134 (2006), 624–648.Google Scholar
Centeno, C. C., Dourado, M. C., Penso, L. D., Rautenbach, D. and Szwarcfiter, J. L., ‘Irreversible conversion of graphs’, Theoret. Comput. Sci. 412 (2011), 3693–3700.Google Scholar
Chang, C.-L. and Lyuu, Y.-D., ‘Spreading messages’, Theoret. Comput. Sci. 410 (2009), 2714–2724.CrossRefGoogle Scholar
Chang, C.-L. and Lyuu, Y.-D., On irreversible dynamic monopolies in general graphs, www.arXiv.org.Google Scholar
Chang, C.-L. and Lyuu, Y.-D., ‘Bounding the sizes of dynamic monopolies and convergent sets for threshold-based cascades’, Theoret. Comput. Sci. 468 (2013), 37–49.Google Scholar
Chen, N., ‘On the approximability of influence in social networks’, SIAM J. Discrete Math. 23 (2009), 1400–1415.Google Scholar
Chiang, C.-Y., Huang, L.-H., Li, B.-J., Wu, J. and Yeh, H.-G., ‘Some results on the target set selection problem’, J. Comb. Optim. 25 (2013), 702–715.Google Scholar
Domingos, P. and Richardson, M., ‘Mining the network value of customers’, Proc. 7th ACM Int. Conf. on Knowledge Discovery and Data Mining (KDD), (2001), 57–66.Google Scholar
Dreyer, P. A. and Roberts, F. S., ‘Irreversible k-threshold processes: graph-theoretical threshold models of the spread of disease and of opinion’, Discrete Appl. Math. 157 (2009), 1615–1627.Google Scholar
Flocchini, P., Kralovic, R., Roncato, A., Ruzicka, P. and Santoro, N., ‘On time versus size for monotone dynamic monopolies in regular topologies’, J. Discrete Algorithms 1 (2003), 129–150.Google Scholar
Grimmett, G. R. and Stirzaker, D. R., Probability and Random Processes, 2nd edn (Oxford University Press, Oxford, 1992).Google Scholar
Khoshkhah, K., Soltani, H. and Zaker, M., ‘On dynamic monopolies of graphs: The average and strict majority thresholds’, Discrete Optim. 9 (2012), 77–83.Google Scholar
Khoshkhah, K., Soltani, H. and Zaker, M., ‘Dynamic monopolies in directed graphs: The spread of unilateral influence in social networks’, Discrete Appl. Math. 171 (2014), 81–89.CrossRefGoogle Scholar
Kulich, T., ‘Dynamic monopolies with randomized starting configuration’, Theoret. Comput. Sci. 412 (2011), 6371–6381.CrossRefGoogle Scholar
McDiarmid, C., ‘Concentration’, in: Probabilistic Methods for Algorithmic Discrete Mathematics (Springer, New York, 1998).Google Scholar
Nichterlein, A., Niedermeier, R., Uhlmann, J. and Weller, M., ‘On tractable cases of target set selection’, in: Algorithms and computation. Part I, Lecture Notes in Computer Science, 6506 (Springer, Berlin, 2010).Google Scholar
Zaker, M., ‘On dynamic monopolies of graphs with general thresholds’, Discrete Math. 312 (2012), 1136–1143.Google Scholar
Zaker, M., ‘Generalized degeneracy, dynamic monopolies and maximum degenerate subgraphs’, Discrete Appl. Math. 161 (2013), 2716–2723.Google Scholar