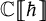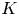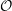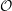Refine search
Actions for selected content:
21 results
Semi-discrete unbalanced optimal transport and quantization
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 17 October 2025, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
3 - The Time-Independent Schrödinger Equation
-
- Book:
- A Computational Introduction to Quantum Physics
- Published online:
- 24 April 2024
- Print publication:
- 25 April 2024, pp 37-56
-
- Chapter
- Export citation

Quantum Geometry, Matrix Theory, and Gravity
-
- Published online:
- 04 April 2024
- Print publication:
- 11 April 2024
The restricted quantum double of the Yangian
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 16 February 2024, pp. 770-841
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chapter 8 - Speech Coding
-
- Book:
- Wireless Communications
- Published online:
- 22 March 2024
- Print publication:
- 08 February 2024, pp 415-446
-
- Chapter
- Export citation
2 - Field Quantization
-
- Book:
- Introductory Quantum Optics
- Published online:
- 14 December 2023
- Print publication:
- 30 November 2023, pp 11-49
-
- Chapter
- Export citation

The Classical–Quantum Correspondence
-
- Published online:
- 16 December 2022
- Print publication:
- 19 January 2023
-
- Element
- Export citation
1 - Stern-Gerlach Experiments
-
- Book:
- Quantum Mechanics
- Published online:
- 11 February 2023
- Print publication:
- 15 September 2022, pp 1-33
-
- Chapter
- Export citation
2 - Quantum Mechanics
-
- Book:
- Quantum Information and Quantum Optics with Superconducting Circuits
- Published online:
- 04 August 2022
- Print publication:
- 18 August 2022, pp 7-18
-
- Chapter
- Export citation
Steenrod operators, the Coulomb branch and the Frobenius twist
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 04 November 2021, pp. 2494-2552
- Print publication:
- November 2021
-
- Article
- Export citation
5 - Reduplication as Summation
-
-
- Book:
- Countability in Natural Language
- Published online:
- 11 June 2021
- Print publication:
- 01 July 2021, pp 145-160
-
- Chapter
- Export citation

Countability in Natural Language
-
- Published online:
- 11 June 2021
- Print publication:
- 01 July 2021
Every symplectic manifold is a (linear) coadjoint orbit
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 18 May 2021, pp. 345-360
- Print publication:
- June 2022
-
- Article
- Export citation
32 - Moduli Space; Soliton Scattering in Moduli Space Approximation; Collective Coordinates
- from Part II - Solitons and Topology; Non-Abelian Theory
-
- Book:
- Classical Field Theory
- Published online:
- 04 March 2019
- Print publication:
- 14 March 2019, pp 294-306
-
- Chapter
- Export citation
Uniform decomposition of probability measures: quantization, clustering and rate of convergence
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1037-1045
- Print publication:
- December 2018
-
- Article
- Export citation
On categories
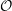 ${\mathcal{O}}$ for quantized symplectic resolutions
${\mathcal{O}}$ for quantized symplectic resolutions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 07 September 2017, pp. 2445-2481
- Print publication:
- December 2017
-
- Article
- Export citation
Dimensionality reduction of visual features for efficient retrieval and classification
-
- Journal:
- APSIPA Transactions on Signal and Information Processing / Volume 5 / 2016
- Published online by Cambridge University Press:
- 12 July 2016, e14
- Print publication:
- 2016
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Numerical Methods for the Exit Time of a Piecewise-Deterministic Markov Process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 196-225
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Approximation by finitely supported measures
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 13 April 2011, pp. 343-359
- Print publication:
- April 2012
-
- Article
- Export citation
The TanDEM-X mission: overview and interferometric performance
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 2 / Issue 3-4 / August 2010
- Published online by Cambridge University Press:
- 07 July 2010, pp. 379-389
-
- Article
- Export citation