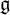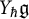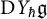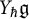1 Introduction
This article is a continuation of [Reference Wendlandt41], which studied the Yangian double
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
associated with an arbitrary symmetrizable Kac–Moody algebra
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
associated with an arbitrary symmetrizable Kac–Moody algebra
![]() $\mathfrak {g}$
through the lens of a
$\mathfrak {g}$
through the lens of a
![]() $\mathbb {Z}$
-graded algebra homomorphism
$\mathbb {Z}$
-graded algebra homomorphism
Here,
![]() $\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
is a naturally defined
$\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
is a naturally defined
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra, described explicitly in Lemma 4.5, and
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra, described explicitly in Lemma 4.5, and
![]() $Y_{\hbar }\mathfrak {g}$
is the Yangian of
$Y_{\hbar }\mathfrak {g}$
is the Yangian of
![]() $\mathfrak {g}$
, defined over
$\mathfrak {g}$
, defined over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. This homomorphism, called the formal shift operator, naturally extends the so-called shift homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. This homomorphism, called the formal shift operator, naturally extends the so-called shift homomorphism
![]() $\tau _z$
on the Yangian, and has a number of remarkable properties. For instance, it induces a family of isomorphisms between completions of
$\tau _z$
on the Yangian, and has a number of remarkable properties. For instance, it induces a family of isomorphisms between completions of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
and
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
and
![]() $Y_{\hbar }\mathfrak {g}$
, realizes
$Y_{\hbar }\mathfrak {g}$
, realizes
![]() $Y_{\hbar }\mathfrak {g}$
as a degeneration of
$Y_{\hbar }\mathfrak {g}$
as a degeneration of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
, and is injective provided
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
, and is injective provided
![]() $\mathfrak {g}$
is of finite type or of simply laced affine type. In addition, it was applied in [Reference Gautam and Wendlandt18] to characterize the category of finite-dimensional representations of
$\mathfrak {g}$
is of finite type or of simply laced affine type. In addition, it was applied in [Reference Gautam and Wendlandt18] to characterize the category of finite-dimensional representations of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
, for
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
, for
![]() ${\hbar }\in \mathbb {C}^\times $
and
${\hbar }\in \mathbb {C}^\times $
and
![]() $\mathfrak {g}$
of finite type, as the tensor-closed Serre subcategory of that of the Yangian consisting of those representations which have no poles at zero.
$\mathfrak {g}$
of finite type, as the tensor-closed Serre subcategory of that of the Yangian consisting of those representations which have no poles at zero.
In this article, we narrow our focus to the case where
![]() $\mathfrak {g}$
is a finite-dimensional simple Lie algebra, and apply these results in conjunction with those of the recent article [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17] to prove one of the main conjectures from the work [Reference Khoroshkin and Tolstoy32] of Khoroshkin and Tolstoy. Namely, we establish that
$\mathfrak {g}$
is a finite-dimensional simple Lie algebra, and apply these results in conjunction with those of the recent article [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17] to prove one of the main conjectures from the work [Reference Khoroshkin and Tolstoy32] of Khoroshkin and Tolstoy. Namely, we establish that
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
, which is defined by doubling the generators of
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
, which is defined by doubling the generators of
![]() $Y_{\hbar }\mathfrak {g}$
(see Definition 4.1), is isomorphic to the restricted quantum double of the Yangian
$Y_{\hbar }\mathfrak {g}$
(see Definition 4.1), is isomorphic to the restricted quantum double of the Yangian
![]() $Y_{\hbar }\mathfrak {g}$
, where the prefix “restricted” indicates that all duality operations are taken so as to respect the underlying gradings. As a consequence of this result and its proof, we find that
$Y_{\hbar }\mathfrak {g}$
, where the prefix “restricted” indicates that all duality operations are taken so as to respect the underlying gradings. As a consequence of this result and its proof, we find that
![]() $\Phi _z$
identifies the universal R-matrix of
$\Phi _z$
identifies the universal R-matrix of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
, which arises from the quantum double construction, with Drinfeld’s universal R-matrix
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
, which arises from the quantum double construction, with Drinfeld’s universal R-matrix
![]() $\mathcal {R}(z)\in (Y_{\hbar }\mathfrak {g}\otimes Y_{\hbar }\mathfrak {g})[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. Our argument makes essential use of the constructive proof of the existence of
$\mathcal {R}(z)\in (Y_{\hbar }\mathfrak {g}\otimes Y_{\hbar }\mathfrak {g})[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. Our argument makes essential use of the constructive proof of the existence of
![]() $\mathcal {R}(z)$
given in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17], which is independent from Drinfeld’s cohomological construction of
$\mathcal {R}(z)$
given in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17], which is independent from Drinfeld’s cohomological construction of
![]() $\mathcal {R}(z)$
from the foundational article [Reference Drinfel’d6].
$\mathcal {R}(z)$
from the foundational article [Reference Drinfel’d6].
1.1 Main results
Let us now sketch our main results in detail. The two results alluded to above form Parts (1) and (2) of the following theorem.
Theorem I There is a unique
![]() $\mathbb {Z}$
-graded Hopf algebra structure on
$\mathbb {Z}$
-graded Hopf algebra structure on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
over
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
such that the formal shift operator
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
such that the formal shift operator
intertwines the Hopf structures on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
and
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
and
![]() $Y_{\hbar }\mathfrak {g}$
. Moreover:
$Y_{\hbar }\mathfrak {g}$
. Moreover:
-
(1)
 $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is isomorphic, as a
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is isomorphic, as a
 $\mathbb {Z}$
-graded Hopf algebra, to the restricted quantum double of the Yangian
$\mathbb {Z}$
-graded Hopf algebra, to the restricted quantum double of the Yangian
 $Y_{\hbar }\mathfrak {g}$
.
$Y_{\hbar }\mathfrak {g}$
. -
(2) Under the above identifications, the universal R-matrix
 of
of
 $\mathrm {D}Y_{\hbar }\mathfrak {g}$
satisfies
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
satisfies 
This is a combination of the three main results of this article: Theorems 7.5, 8.4, and 9.6. Part (1) is the statement of our second main result – Theorem 8.4 – and is precisely the variant of the conjecture from [Reference Khoroshkin and Tolstoy32, Section 2], which we establish in the present article. Our approach to proving it is, in a certain sense, dual to the strategy outlined in [Reference Khoroshkin and Tolstoy32], which was brought to fruition for
![]() $\mathfrak {g}=\mathfrak {s}\mathfrak {l}_2$
. In more detail, our argument hinges on the fact, proven in Proposition 7.1, that the universal R-matrix
$\mathfrak {g}=\mathfrak {s}\mathfrak {l}_2$
. In more detail, our argument hinges on the fact, proven in Proposition 7.1, that the universal R-matrix
![]() $\mathcal {R}(z)$
of the Yangian gives rise to a
$\mathcal {R}(z)$
of the Yangian gives rise to a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
which is compatible with the Hopf algebra structure on
![]() $Y_{\hbar }\mathfrak {g}$
and the co-opposite Hopf structure on the dual
$Y_{\hbar }\mathfrak {g}$
and the co-opposite Hopf structure on the dual
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
of the Yangian
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
of the Yangian
![]() $Y_{\hbar }\mathfrak {g}$
taken in the category of
$Y_{\hbar }\mathfrak {g}$
taken in the category of
![]() $\mathbb {Z}$
-graded quantized enveloping algebras. That is,
$\mathbb {Z}$
-graded quantized enveloping algebras. That is,
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is the restricted (or graded) dual of the Drinfeld–Gavarini [Reference Drinfel’d7, Reference Gavarini19] subalgebra
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is the restricted (or graded) dual of the Drinfeld–Gavarini [Reference Drinfel’d7, Reference Gavarini19] subalgebra
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\subset Y_{\hbar }\mathfrak {g}$
, defined in Section 5, and provides a homogeneous quantization of the restricted dual
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\subset Y_{\hbar }\mathfrak {g}$
, defined in Section 5, and provides a homogeneous quantization of the restricted dual
![]() $t^{-1}\mathfrak {g}[t^{-1}]$
to the
$t^{-1}\mathfrak {g}[t^{-1}]$
to the
![]() $\mathbb {N}$
-graded Lie bialgebra
$\mathbb {N}$
-graded Lie bialgebra
![]() $\mathfrak {g}[t]$
, as we prove in detail in Section 6 (see Theorem 6.7).
$\mathfrak {g}[t]$
, as we prove in detail in Section 6 (see Theorem 6.7).
Using the construction of
![]() $\mathcal {R}(z)$
given in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17] and properties of
$\mathcal {R}(z)$
given in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17] and properties of
![]() $\Phi _z$
established in [Reference Wendlandt41], we deduce that the image of
$\Phi _z$
established in [Reference Wendlandt41], we deduce that the image of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
under
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
under ![]() is contained in the image of
is contained in the image of
![]() $\Phi _z$
. We may thus compose
$\Phi _z$
. We may thus compose ![]() with
with
![]() $\Phi _z^{-1}$
to obtain a
$\Phi _z^{-1}$
to obtain a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
where ![]() . In our first main result – Theorem 7.5 – we show that there is a unique
. In our first main result – Theorem 7.5 – we show that there is a unique
![]() $\mathbb {Z}$
-graded Hopf algebra structure on
$\mathbb {Z}$
-graded Hopf algebra structure on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
for which both
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
for which both
![]() $\check {\imath }$
and the natural inclusion
$\check {\imath }$
and the natural inclusion
![]() $\imath :Y_{\hbar }\mathfrak {g}\to \mathrm {D}Y_{\hbar }\mathfrak {g}$
are injective homomorphisms of graded Hopf algebras. This is exactly the Hopf structure alluded to in the statement of Theorem I, and is such that
$\imath :Y_{\hbar }\mathfrak {g}\to \mathrm {D}Y_{\hbar }\mathfrak {g}$
are injective homomorphisms of graded Hopf algebras. This is exactly the Hopf structure alluded to in the statement of Theorem I, and is such that
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
provides a homogeneous quantization of the restricted Drinfeld double
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
provides a homogeneous quantization of the restricted Drinfeld double
![]() $\mathfrak {g}[t^{\pm 1}]$
of
$\mathfrak {g}[t^{\pm 1}]$
of
![]() $\mathfrak {g}[t]$
. Using Theorem 7.5, it is then not difficult to establish Part (1) above (i.e., Theorem 8.4) using the double cross-product realization of the restricted quantum double (see Section 8.2).
$\mathfrak {g}[t]$
. Using Theorem 7.5, it is then not difficult to establish Part (1) above (i.e., Theorem 8.4) using the double cross-product realization of the restricted quantum double (see Section 8.2).
Our third and final main result, Theorem 9.6, is a strengthening of Part (2) above. Indeed, it outputs the Gauss decomposition for ![]() while identifying each factor appearing in this decomposition with the factors
while identifying each factor appearing in this decomposition with the factors
![]() $\mathcal {R}^\pm (z)$
and
$\mathcal {R}^\pm (z)$
and
![]() $\mathcal {R}^0(z)$
of
$\mathcal {R}^0(z)$
of
![]() $\mathcal {R}(z)$
, which were studied in detail in [Reference Gautam and Toledano Laredo16, Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17].
$\mathcal {R}(z)$
, which were studied in detail in [Reference Gautam and Toledano Laredo16, Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17].
1.2 Motivation
Part (2) of Theorem I implies that
![]() $\mathcal {R}(z)$
can be recovered from the canonical element defined by the pairing between
$\mathcal {R}(z)$
can be recovered from the canonical element defined by the pairing between
![]() $Y_{\hbar }\mathfrak {g}$
and its restricted dual
$Y_{\hbar }\mathfrak {g}$
and its restricted dual
![]() $Y_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \subset \mathrm {D}Y_{\hbar }\mathfrak {g}$
by applying the injection
$Y_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \subset \mathrm {D}Y_{\hbar }\mathfrak {g}$
by applying the injection ![]() to its second tensor factor:
to its second tensor factor:
Here, we refer the reader to Theorem 9.6 for further details, which takes into account the topological subtleties surrounding this statement. Obtaining this interpretation of
![]() $\mathcal {R}(z)$
is in fact our original motivation for addressing the conjecture of [Reference Khoroshkin and Tolstoy32, Section 2], and brings the theory surrounding the universal R-matrix of the Yangian to a more equal footing with that of the (extended, untwisted) quantum affine algebra
$\mathcal {R}(z)$
is in fact our original motivation for addressing the conjecture of [Reference Khoroshkin and Tolstoy32, Section 2], and brings the theory surrounding the universal R-matrix of the Yangian to a more equal footing with that of the (extended, untwisted) quantum affine algebra
![]() $U_q(\widehat {\mathfrak {g}})$
and the quantum loop algebra
$U_q(\widehat {\mathfrak {g}})$
and the quantum loop algebra
![]() $U_q(L\mathfrak {g})$
. The differences are, however, still quite pronounced. Indeed,
$U_q(L\mathfrak {g})$
. The differences are, however, still quite pronounced. Indeed,
![]() $U_q(\widehat {\mathfrak {g}})$
is itself nearly the quantum double of its (quantum Kac–Moody) Borel subalgebra
$U_q(\widehat {\mathfrak {g}})$
is itself nearly the quantum double of its (quantum Kac–Moody) Borel subalgebra
![]() $U_q({\mathfrak {b}}^+)$
, and its universal R-matrix
$U_q({\mathfrak {b}}^+)$
, and its universal R-matrix
![]() $\mathscr {R}$
lies in a completion of
$\mathscr {R}$
lies in a completion of
![]() $U_q({\mathfrak {b}}^+)\otimes U_q({\mathfrak {b}}^-)$
. One then recovers the universal R-matrix
$U_q({\mathfrak {b}}^+)\otimes U_q({\mathfrak {b}}^-)$
. One then recovers the universal R-matrix
![]() $\mathscr {R}_{L\mathfrak {g}}$
of
$\mathscr {R}_{L\mathfrak {g}}$
of
![]() $U_q(L\mathfrak {g})$
as a truncation of
$U_q(L\mathfrak {g})$
as a truncation of
![]() $\mathscr {R}$
, and its z-dependent analogue is
$\mathscr {R}$
, and its z-dependent analogue is
where
![]() $D_z$
is given by the
$D_z$
is given by the
![]() $\mathbb {Z}$
-grading on
$\mathbb {Z}$
-grading on
![]() $U_q(L\mathfrak {g})$
(see [Reference Etingof, Frenkel and Kirillov10, Section 9.4] or [Reference Frenkel and Reshetikhin14, Section 4], for instance). Crucially,
$U_q(L\mathfrak {g})$
(see [Reference Etingof, Frenkel and Kirillov10, Section 9.4] or [Reference Frenkel and Reshetikhin14, Section 4], for instance). Crucially,
![]() $\mathscr {R}$
can be constructed by computing dual bases with respect to the pairing between
$\mathscr {R}$
can be constructed by computing dual bases with respect to the pairing between
![]() $U_q({\mathfrak {b}}^+)$
and
$U_q({\mathfrak {b}}^+)$
and
![]() $U_q({\mathfrak {b}}^-)$
, and was done explicitly by Damiani in [Reference Damiani5]. In contrast, the Yangian
$U_q({\mathfrak {b}}^-)$
, and was done explicitly by Damiani in [Reference Damiani5]. In contrast, the Yangian
![]() $Y_{\hbar }\mathfrak {g}$
is not of Kac–Moody type and does not arise as a Hopf algebra from the quantum double construction applied to any analogue of
$Y_{\hbar }\mathfrak {g}$
is not of Kac–Moody type and does not arise as a Hopf algebra from the quantum double construction applied to any analogue of
![]() $U_q({\mathfrak {b}}^+)$
.Footnote
1
In addition,
$U_q({\mathfrak {b}}^+)$
.Footnote
1
In addition,
![]() $\mathcal {R}(z)$
and
$\mathcal {R}(z)$
and
![]() $\mathscr {R}_{L\mathfrak {g}}(z)$
exhibit significantly different analytic behaviour when evaluated on finite-dimensional representations [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17]. Nonetheless, the results of this article further cement that there are very strong parallels to be drawn between the two pictures. Indeed, one obtains the
$\mathscr {R}_{L\mathfrak {g}}(z)$
exhibit significantly different analytic behaviour when evaluated on finite-dimensional representations [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17]. Nonetheless, the results of this article further cement that there are very strong parallels to be drawn between the two pictures. Indeed, one obtains the
![]() $Y_{\hbar }\mathfrak {g}$
-analogue of the above story by replacing
$Y_{\hbar }\mathfrak {g}$
-analogue of the above story by replacing
![]() $U_q({\mathfrak {b}}^+)$
by
$U_q({\mathfrak {b}}^+)$
by
![]() $Y_{\hbar }\mathfrak {g}$
,
$Y_{\hbar }\mathfrak {g}$
,
![]() $U_q(L\mathfrak {g})$
by the Yangian double
$U_q(L\mathfrak {g})$
by the Yangian double
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
, and
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
, and
![]() $D_z$
by the formal shift operator
$D_z$
by the formal shift operator
![]() $\Phi _z$
.
$\Phi _z$
.
It should be noted that it appears that this realization of
![]() $\mathcal {R}(z)$
has been anticipated for some time in the mathematical physics community; see, for instance, [Reference Stukopin40, Section 5], which considers its super-analogue. The direction taken therein is, however, based on both the conjecture from [Reference Khoroshkin and Tolstoy32, Section 2] at the heart of the present article, and on the infinite product formulas for the factors
$\mathcal {R}(z)$
has been anticipated for some time in the mathematical physics community; see, for instance, [Reference Stukopin40, Section 5], which considers its super-analogue. The direction taken therein is, however, based on both the conjecture from [Reference Khoroshkin and Tolstoy32, Section 2] at the heart of the present article, and on the infinite product formulas for the factors ![]() of
of ![]() given [Reference Khoroshkin and Tolstoy32, Section 5], which remain conjectural. Some more discussion on this point is given in Section 9.4.
given [Reference Khoroshkin and Tolstoy32, Section 5], which remain conjectural. Some more discussion on this point is given in Section 9.4.
1.3 Remarks
Let us now give a few brief remarks. First, it is essential that the Yangian double
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is defined as a topological algebra over
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is defined as a topological algebra over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
for the above results to hold true. To expand on this,
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
for the above results to hold true. To expand on this,
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
can be realized as the
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
can be realized as the
![]() ${\hbar }$
-adic completion of a
${\hbar }$
-adic completion of a
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-algebra
$\mathbb {C}[{\hbar }]$
-algebra
![]() $ {D}Y_{{\hbar }}\mathfrak {g}^\jmath $
defined by generators and relations (see Remark 4.2). One can further specialize
$ {D}Y_{{\hbar }}\mathfrak {g}^\jmath $
defined by generators and relations (see Remark 4.2). One can further specialize
![]() ${\hbar }$
to any nonzero complex number
${\hbar }$
to any nonzero complex number
![]() $\zeta $
to obtain a
$\zeta $
to obtain a
![]() $\mathbb {C}$
-algebra
$\mathbb {C}$
-algebra
![]() $ {D}Y_\zeta \mathfrak {g}= {D}Y_{{\hbar }}\mathfrak {g}^\jmath /({\hbar }-\zeta ) {D}Y_{{\hbar }}\mathfrak {g}^\jmath $
, whose category of finite-dimensional representations was characterized in terms of that of the corresponding Yangian
$ {D}Y_\zeta \mathfrak {g}= {D}Y_{{\hbar }}\mathfrak {g}^\jmath /({\hbar }-\zeta ) {D}Y_{{\hbar }}\mathfrak {g}^\jmath $
, whose category of finite-dimensional representations was characterized in terms of that of the corresponding Yangian
![]() $Y_\zeta (\mathfrak {g})$
in [Reference Gautam and Wendlandt18]. Though this category has a tensor structure which corresponds to the Hopf structure on
$Y_\zeta (\mathfrak {g})$
in [Reference Gautam and Wendlandt18]. Though this category has a tensor structure which corresponds to the Hopf structure on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
, it is important to note that
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
, it is important to note that
![]() $ {D}Y_\zeta \mathfrak {g}$
is not a Hopf algebra over
$ {D}Y_\zeta \mathfrak {g}$
is not a Hopf algebra over
![]() $\mathbb {C}$
, and in particular it does not coincide with the (restricted) quantum double of
$\mathbb {C}$
, and in particular it does not coincide with the (restricted) quantum double of
![]() $Y_\zeta (\mathfrak {g})$
defined in any reasonable sense.
$Y_\zeta (\mathfrak {g})$
defined in any reasonable sense.
That being said,
![]() $ {D}Y_\zeta \mathfrak {g}$
admits a natural
$ {D}Y_\zeta \mathfrak {g}$
admits a natural
![]() $\mathbb {Z}$
-filtration corresponding to the
$\mathbb {Z}$
-filtration corresponding to the
![]() $\mathbb {Z}$
-grading on
$\mathbb {Z}$
-grading on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
, and the expectation is that the formal completion of
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
, and the expectation is that the formal completion of
![]() $ {D}Y_\zeta \mathfrak {g}$
with respect to this filtration coincides with the (restricted) quantum double of
$ {D}Y_\zeta \mathfrak {g}$
with respect to this filtration coincides with the (restricted) quantum double of
![]() $Y_\zeta (\mathfrak {g})$
taken in the appropriate category of
$Y_\zeta (\mathfrak {g})$
taken in the appropriate category of
![]() $\mathbb {Z}$
-filtered, complete topological Hopf algebras. This is in fact the version of Part (2) of Theorem I conjectured in [Reference Khoroshkin and Tolstoy32], and is consistent with the situation that transpires in type A for the R-matrix realization of the Yangian, which has been developed in great detail in the recent article [Reference Nazarov38]. For our purposes, it is more natural to work over
$\mathbb {Z}$
-filtered, complete topological Hopf algebras. This is in fact the version of Part (2) of Theorem I conjectured in [Reference Khoroshkin and Tolstoy32], and is consistent with the situation that transpires in type A for the R-matrix realization of the Yangian, which has been developed in great detail in the recent article [Reference Nazarov38]. For our purposes, it is more natural to work over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
within the framework of quantized enveloping algebras first developed by Drinfeld [Reference Drinfel’d7], where we may study
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
within the framework of quantized enveloping algebras first developed by Drinfeld [Reference Drinfel’d7], where we may study
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
from the point of view of quantization of Lie bialgebras. At the same time, many of our results are “global” (in the sense of [Reference Gavarini20]) and admit an interpretation over both
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
from the point of view of quantization of Lie bialgebras. At the same time, many of our results are “global” (in the sense of [Reference Gavarini20]) and admit an interpretation over both
![]() $\mathbb {C}[{\hbar }]$
and
$\mathbb {C}[{\hbar }]$
and
![]() $\mathbb {C}$
, including the realization of
$\mathbb {C}$
, including the realization of
![]() $\mathcal {R}(z)$
provided by Theorem 9.6 (see Appendix A).
$\mathcal {R}(z)$
provided by Theorem 9.6 (see Appendix A).
1.4 Outline
The article is written so as to provide a complete picture, accessible to non-experts, where possible. For this reason, we take great care to lay the foundation needed to state and prove the results outlined in Section 1.1. The first three sections – Sections 2–4 – are intended to serve a preliminary role: Section 2 surveys the theory of
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules, algebras, and Hopf algebras, including homogeneous quantizations of graded Lie bialgebras. This theory plays a prominent role throughout the article. In Section 3, we review the definition and main properties of the Yangian
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules, algebras, and Hopf algebras, including homogeneous quantizations of graded Lie bialgebras. This theory plays a prominent role throughout the article. In Section 3, we review the definition and main properties of the Yangian
![]() $Y_{\hbar }\mathfrak {g}$
, defined both over
$Y_{\hbar }\mathfrak {g}$
, defined both over
![]() $\mathbb {C}[{\hbar }]$
and
$\mathbb {C}[{\hbar }]$
and
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. Notably, this includes a review of the construction of the universal R-matrix
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. Notably, this includes a review of the construction of the universal R-matrix
![]() $\mathcal {R}(z)$
carried out in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17]. Section 4 is focused on the Yangian double
$\mathcal {R}(z)$
carried out in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17]. Section 4 is focused on the Yangian double
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
and, in particular, on reviewing the main results of [Reference Wendlandt41] (see Theorems 4.6 and 4.8).
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
and, in particular, on reviewing the main results of [Reference Wendlandt41] (see Theorems 4.6 and 4.8).
In Sections 5 and 6, we study the Drinfeld–Gavarini subalgebra
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
of the Yangian, its
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
of the Yangian, its
![]() $\mathbb {C}[{\hbar }]$
-form, and its restricted dual
$\mathbb {C}[{\hbar }]$
-form, and its restricted dual
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
in detail. This includes a detailed proof that
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
in detail. This includes a detailed proof that
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
provides a homogeneous quantization of
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
provides a homogeneous quantization of
![]() $t^{-1}\mathfrak {g}[t^{-1}]$
, equipped with the Yangian Lie bialgebra structure (see Definition 6.1 and Theorem 6.7).
$t^{-1}\mathfrak {g}[t^{-1}]$
, equipped with the Yangian Lie bialgebra structure (see Definition 6.1 and Theorem 6.7).
The last three sections of the article contain its three main results: Theorems 7.5, 8.4, and 9.6. We refer the reader to Section 1.1 above, where these are outlined in detail. Finally, in Appendix Appendix A, we explain how to translate the construction of the universal R-matrix given in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17] for
![]() ${\hbar }\in \mathbb {C}^\times $
to the setting of the present article, in which
${\hbar }\in \mathbb {C}^\times $
to the setting of the present article, in which
![]() ${\hbar }$
is a formal variable (see Proposition A.1, which appears in Section 3.6 as Theorem 3.8).
${\hbar }$
is a formal variable (see Proposition A.1, which appears in Section 3.6 as Theorem 3.8).
2 Homogeneous quantizations
2.1 Topological modules
Recall that a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module
![]() $\mathsf {M}$
is separated if the intersection of the family of submodules
$\mathsf {M}$
is separated if the intersection of the family of submodules
![]() ${\hbar }^n\mathsf {M}$
is trivial, and it is complete if the natural
${\hbar }^n\mathsf {M}$
is trivial, and it is complete if the natural
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear map
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear map
is surjective, where the inverse limit is taken over the set
![]() $\mathbb {N}$
of nonnegative integers. In particular,
$\mathbb {N}$
of nonnegative integers. In particular,
![]() $\mathsf {M}$
is both separated and complete if and only if the above map is an isomorphism. If
$\mathsf {M}$
is both separated and complete if and only if the above map is an isomorphism. If
![]() $\mathsf {M}$
is separated, complete, and torsion-free as a
$\mathsf {M}$
is separated, complete, and torsion-free as a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module, then it is said to be topologically free. This is equivalent to the existence of a
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module, then it is said to be topologically free. This is equivalent to the existence of a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module isomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module isomorphism
![]() $\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
for a complex vector space
$\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
for a complex vector space
![]() $\mathsf {V}$
. Such an isomorphism is specified by a choice of complement
$\mathsf {V}$
. Such an isomorphism is specified by a choice of complement
![]() $\mathsf {V}\subset \mathsf {M}$
to
$\mathsf {V}\subset \mathsf {M}$
to
![]() ${\hbar }\mathsf {M}$
:
${\hbar }\mathsf {M}$
:
More generally, if
![]() $\mathsf {M}$
is any
$\mathsf {M}$
is any
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module, then the space
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module, then the space
![]() $\mathsf {V}=\mathsf {M}/{\hbar }\mathsf {M}$
is called the semiclassical limit of
$\mathsf {V}=\mathsf {M}/{\hbar }\mathsf {M}$
is called the semiclassical limit of
![]() $\mathsf {M}$
. Similarly, the semiclassical limit of a
$\mathsf {M}$
. Similarly, the semiclassical limit of a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear map
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear map
![]() is the
is the
![]() $\mathbb {C}$
-linear map
$\mathbb {C}$
-linear map ![]() uniquely determined by the commutativity of the diagram
uniquely determined by the commutativity of the diagram

As the following elementary result illustrates, the semiclassical limit of a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphism encodes important information about the original map.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphism encodes important information about the original map.
Lemma 2.1 Let
![]() $\mathsf {M}$
,
$\mathsf {M}$
,
![]() $\mathsf {N}$
,
$\mathsf {N}$
,
![]() , and
, and
![]() be as above.
be as above.
-
(1) Suppose that
 $\mathsf {M}$
is separated,
$\mathsf {M}$
is separated,
 $\mathsf {N}$
is torsion-free, and
$\mathsf {N}$
is torsion-free, and
 is injective. Then
is injective. Then
 is injective.
is injective. -
(2) Suppose that
 $\mathsf {M}$
is complete,
$\mathsf {M}$
is complete,
 $\mathsf {N}$
is separated, and
$\mathsf {N}$
is separated, and
 is surjective. Then
is surjective. Then
 is surjective.
is surjective.
The topological tensor product
![]() $\mathsf {M} \,{\widehat {\otimes }}\, \mathsf {N}$
of two
$\mathsf {M} \,{\widehat {\otimes }}\, \mathsf {N}$
of two
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
![]() $\mathsf {M}$
and
$\mathsf {M}$
and
![]() $\mathsf {N}$
is the
$\mathsf {N}$
is the
![]() ${\hbar }$
-adic completion of the algebraic tensor product
${\hbar }$
-adic completion of the algebraic tensor product
![]() $\mathsf {M}\otimes _{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}\mathsf {N}$
:
$\mathsf {M}\otimes _{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}\mathsf {N}$
:
If
![]() $\mathsf {M}$
and
$\mathsf {M}$
and
![]() $\mathsf {N}$
are topologically free with
$\mathsf {N}$
are topologically free with
![]() $\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
and
$\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
and
![]() $\mathsf {N}\cong \mathsf {W}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, then
$\mathsf {N}\cong \mathsf {W}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, then
![]() $\mathsf {M} \,{\widehat {\otimes }}\, \mathsf {N}$
is topologically free and isomorphic to
$\mathsf {M} \,{\widehat {\otimes }}\, \mathsf {N}$
is topologically free and isomorphic to
![]() $(\mathsf {V}\otimes _{\mathbb {C}} \mathsf {W})[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
.
$(\mathsf {V}\otimes _{\mathbb {C}} \mathsf {W})[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
.
In this article, we shall say that
![]() $\mathsf {M}$
is a topological module over
$\mathsf {M}$
is a topological module over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
if
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
if
![]() $\mathsf {M}$
is a
$\mathsf {M}$
is a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module which is both separated and complete. For any such module, we have
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module which is both separated and complete. For any such module, we have
Similarly, by a topological algebra
![]() $\mathsf {A}$
over
$\mathsf {A}$
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, we shall always mean that
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, we shall always mean that
![]() $\mathsf {A}$
is a
$\mathsf {A}$
is a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra which is both separated and complete as a module over
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra which is both separated and complete as a module over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. In particular, the multiplication m can be viewed as a
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. In particular, the multiplication m can be viewed as a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear map
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear map
A topological Hopf algebra
![]() $\mathsf {H}$
over
$\mathsf {H}$
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
is a topological
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
is a topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra equipped with a counit
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra equipped with a counit
![]() $\varepsilon :\mathsf {H}\to \mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, a coproduct
$\varepsilon :\mathsf {H}\to \mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, a coproduct
![]() $\Delta :\mathsf {H}\to \mathsf {H} \, \widehat {\otimes }\, \mathsf {H}$
, and an antipode
$\Delta :\mathsf {H}\to \mathsf {H} \, \widehat {\otimes }\, \mathsf {H}$
, and an antipode
![]() $S:\mathsf {H}\to \mathsf {H}$
which collectively satisfy the axioms of a Hopf algebra with all tensor products given by the topological tensor product
$S:\mathsf {H}\to \mathsf {H}$
which collectively satisfy the axioms of a Hopf algebra with all tensor products given by the topological tensor product
![]() $\widehat {\otimes }$
. By modifying these definitions in the expected way, one obtains the notion of a topological coalgebra and bialgebra over
$\widehat {\otimes }$
. By modifying these definitions in the expected way, one obtains the notion of a topological coalgebra and bialgebra over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
.
If
![]() $\mathsf {M}$
and
$\mathsf {M}$
and
![]() $\mathsf {N}$
are topological
$\mathsf {N}$
are topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules and
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules and
![]() $\mathsf {N}\cong \mathsf {W}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
is topologically free, then the space of
$\mathsf {N}\cong \mathsf {W}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
is topologically free, then the space of
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphisms
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphisms
![]() $\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}(\mathsf {M},\mathsf {N})$
is separated, complete, and torsion-free. If, in addition,
$\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}(\mathsf {M},\mathsf {N})$
is separated, complete, and torsion-free. If, in addition,
![]() $\mathsf {M}$
is topologically free with
$\mathsf {M}$
is topologically free with
![]() $\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, then one has
$\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, then one has
In particular, the
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear dual
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear dual
![]() $\mathsf {M}^\ast :=\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}(\mathsf {M},\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])$
of a topologically free
$\mathsf {M}^\ast :=\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}(\mathsf {M},\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])$
of a topologically free
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module
![]() $\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
satisfies
$\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
satisfies
![]() $\mathsf {M}^\ast \cong \mathsf {V}^\ast [\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
.
$\mathsf {M}^\ast \cong \mathsf {V}^\ast [\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
.
2.2 Graded topological modules
Let us now turn toward the
![]() $\mathbb {Z}$
-graded analogues of the above definitions. Henceforth, we view
$\mathbb {Z}$
-graded analogues of the above definitions. Henceforth, we view
![]() $\mathbb {C}[{\hbar }]=\bigoplus _{k\in \mathbb {N}}\mathbb {C}{\hbar }^k$
as an
$\mathbb {C}[{\hbar }]=\bigoplus _{k\in \mathbb {N}}\mathbb {C}{\hbar }^k$
as an
![]() $\mathbb {N}$
-graded ring. For brevity, we shall denote its
$\mathbb {N}$
-graded ring. For brevity, we shall denote its
![]() $\mathbb {N}$
-graded quotient
$\mathbb {N}$
-graded quotient
![]() $\mathbb {C}[{\hbar }]/{\hbar }^n \mathbb {C}[{\hbar }]$
by
$\mathbb {C}[{\hbar }]/{\hbar }^n \mathbb {C}[{\hbar }]$
by
![]() $\mathsf {K}_n$
, for each
$\mathsf {K}_n$
, for each
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Definition 2.2 We say that a topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module
![]() $\mathsf {M}$
is
$\mathsf {M}$
is
![]() $\mathbb {Z}$
-graded if, for each
$\mathbb {Z}$
-graded if, for each
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $\mathsf {M}/{\hbar }^n \mathsf {M}=\bigoplus _{k\in \mathbb {Z}}(\mathsf {M}/{\hbar }^n\mathsf {M})_k$
is a
$\mathsf {M}/{\hbar }^n \mathsf {M}=\bigoplus _{k\in \mathbb {Z}}(\mathsf {M}/{\hbar }^n\mathsf {M})_k$
is a
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathsf {K}_n$
-module and the natural homomorphism
$\mathsf {K}_n$
-module and the natural homomorphism
is
![]() $\mathbb {Z}$
-graded. If
$\mathbb {Z}$
-graded. If
![]() $(\mathsf {M}/{\hbar }^n\mathsf {M})_k$
is trivial for
$(\mathsf {M}/{\hbar }^n\mathsf {M})_k$
is trivial for
![]() $k<0$
, we say that
$k<0$
, we say that
![]() $\mathsf {M}$
is
$\mathsf {M}$
is
![]() $\mathbb {N}$
-graded.
$\mathbb {N}$
-graded.
A
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphism
![]() $\mathsf {M}\to \mathsf {N}$
between
$\mathsf {M}\to \mathsf {N}$
between
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
![]() $\mathsf {M}$
and
$\mathsf {M}$
and
![]() $\mathsf {N}$
is said to be
$\mathsf {N}$
is said to be
![]() $\mathbb {Z}$
-graded if the induced morphisms
$\mathbb {Z}$
-graded if the induced morphisms
are all
![]() $\mathbb {Z}$
-graded. More generally, it is
$\mathbb {Z}$
-graded. More generally, it is
![]() $\mathbb {Z}$
-graded of degree
$\mathbb {Z}$
-graded of degree
![]() $a\in \mathbb {Z}$
if each of these induced morphisms is homogeneous of degree a.
$a\in \mathbb {Z}$
if each of these induced morphisms is homogeneous of degree a.
The category of
![]() $\mathbb {Z}$
-graded topological modules is closed under the tensor product
$\mathbb {Z}$
-graded topological modules is closed under the tensor product
![]() $\widehat {\otimes }$
. Indeed, this follows from the elementary observation that, given two
$\widehat {\otimes }$
. Indeed, this follows from the elementary observation that, given two
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
![]() $\mathsf {M}$
and
$\mathsf {M}$
and
![]() $\mathsf {N}$
, one has
$\mathsf {N}$
, one has
which can be equipped with the standard tensor product grading, provided
![]() $\mathsf {M}/{\hbar }^n\mathsf {M}$
and
$\mathsf {M}/{\hbar }^n\mathsf {M}$
and
![]() $\mathsf {N}/{\hbar }^n\mathsf {N}$
are both
$\mathsf {N}/{\hbar }^n\mathsf {N}$
are both
![]() $\mathbb {Z}$
-graded.
$\mathbb {Z}$
-graded.
Definition 2.3 A topological algebra
![]() $\mathsf {A}$
is said to be
$\mathsf {A}$
is said to be
![]() $\mathbb {Z}$
-graded if it is graded as a topological
$\mathbb {Z}$
-graded if it is graded as a topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module and the multiplication map
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module and the multiplication map
is a
![]() $\mathbb {Z}$
-graded homomorphism. Similarly, a topological Hopf algebra
$\mathbb {Z}$
-graded homomorphism. Similarly, a topological Hopf algebra
![]() $\mathsf {H}$
is
$\mathsf {H}$
is
![]() $\mathbb {Z}$
-graded if it is
$\mathbb {Z}$
-graded if it is
![]() $\mathbb {Z}$
-graded as a topological algebra and the structure maps
$\mathbb {Z}$
-graded as a topological algebra and the structure maps
are all
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphisms. Equivalently, a topological algebra or Hopf algebra
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphisms. Equivalently, a topological algebra or Hopf algebra
![]() $\mathsf {H}$
is
$\mathsf {H}$
is
![]() $\mathbb {Z}$
-graded if the conditions of Definition 2.2 hold and each
$\mathbb {Z}$
-graded if the conditions of Definition 2.2 hold and each
![]() $\mathsf {H}/{\hbar }^n\mathsf {H}$
is a
$\mathsf {H}/{\hbar }^n\mathsf {H}$
is a
![]() $\mathbb {Z}$
-graded algebra or Hopf algebra over
$\mathbb {Z}$
-graded algebra or Hopf algebra over
![]() $\mathsf {K}_n$
, respectively.
$\mathsf {K}_n$
, respectively.
Of course, one also has the notion of a
![]() $\mathbb {Z}$
-graded topological coalgebra and bialgebra, which are defined by making the obvious modifications to the above definition.
$\mathbb {Z}$
-graded topological coalgebra and bialgebra, which are defined by making the obvious modifications to the above definition.
The prototypical example of a
![]() $\mathbb {Z}$
-graded topological module over
$\mathbb {Z}$
-graded topological module over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
is
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
is
![]() $\mathsf {M}=\mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
where
$\mathsf {M}=\mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
where
![]() $\mathsf {V}=\bigoplus _{k\in \mathbb {Z}}\mathsf {V}_k$
is a
$\mathsf {V}=\bigoplus _{k\in \mathbb {Z}}\mathsf {V}_k$
is a
![]() $\mathbb {Z}$
-graded complex vector space. In this case, one has
$\mathbb {Z}$
-graded complex vector space. In this case, one has
which is naturally graded, as
![]() $\mathsf {V}[{\hbar }]$
is graded with
$\mathsf {V}[{\hbar }]$
is graded with
![]() $\mathsf {V}[{\hbar }]_k= \bigoplus _{n\geq 0} {\hbar }^n \mathsf {V}_{k-n}$
, and
$\mathsf {V}[{\hbar }]_k= \bigoplus _{n\geq 0} {\hbar }^n \mathsf {V}_{k-n}$
, and
![]() ${\hbar }^n\mathsf {V}[{\hbar }]$
is a graded submodule. The assertion that
${\hbar }^n\mathsf {V}[{\hbar }]$
is a graded submodule. The assertion that
![]() $\mathsf {M}$
is
$\mathsf {M}$
is
![]() $\mathbb {Z}$
-graded may be recaptured as follows. For each
$\mathbb {Z}$
-graded may be recaptured as follows. For each
![]() $k\in \mathbb {Z}$
, set
$k\in \mathbb {Z}$
, set
Then each
![]() $\mathsf {M}_k$
is a closed subspace of
$\mathsf {M}_k$
is a closed subspace of
![]() $\mathsf {M}$
satisfying
$\mathsf {M}$
satisfying
![]() $\mathsf {M}_k/{\hbar }^n \mathsf {M}_{k-n}\cong (\mathsf {M}/{\hbar }^n\mathsf {M})_k$
, and
$\mathsf {M}_k/{\hbar }^n \mathsf {M}_{k-n}\cong (\mathsf {M}/{\hbar }^n\mathsf {M})_k$
, and
![]() $\mathsf {M}$
contains the
$\mathsf {M}$
contains the
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-module
$\mathbb {C}[{\hbar }]$
-module
![]() $\bigoplus _{k\in \mathbb {Z}}\mathsf {M}_k$
as a dense
$\bigoplus _{k\in \mathbb {Z}}\mathsf {M}_k$
as a dense
![]() $\mathbb {C}[{\hbar }]$
-submodule. Moreover, the
$\mathbb {C}[{\hbar }]$
-submodule. Moreover, the
![]() ${\hbar }$
-adic topology on this submodule coincides with the subspace topology, so
${\hbar }$
-adic topology on this submodule coincides with the subspace topology, so
![]() $\mathsf {M}$
is the
$\mathsf {M}$
is the
![]() ${\hbar }$
-adic completion of
${\hbar }$
-adic completion of
![]() $\bigoplus _{k\in \mathbb {Z}}\mathsf {M}_k$
. If, in addition,
$\bigoplus _{k\in \mathbb {Z}}\mathsf {M}_k$
. If, in addition,
![]() $\mathsf {V}$
is
$\mathsf {V}$
is
![]() $\mathbb {N}$
-graded, then
$\mathbb {N}$
-graded, then
![]() $\bigoplus _{k\in \mathbb {Z}}\mathsf {M}_k$
coincides with the polynomial space
$\bigoplus _{k\in \mathbb {Z}}\mathsf {M}_k$
coincides with the polynomial space
![]() $\mathsf {V}[{\hbar }]\subset \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
.
$\mathsf {V}[{\hbar }]\subset \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
.
The below lemma provides an equivalent characterization of the definition of a
![]() $\mathbb {Z}$
-graded topological module and algebra which generalizes this picture.
$\mathbb {Z}$
-graded topological module and algebra which generalizes this picture.
Lemma 2.4 A topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module
![]() $\mathsf {M}$
is
$\mathsf {M}$
is
![]() $\mathbb {Z}$
-graded if and only if it admits a dense,
$\mathbb {Z}$
-graded if and only if it admits a dense,
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-submodule
$\mathbb {C}[{\hbar }]$
-submodule
with each
![]() $\mathsf {M}_k$
a closed subspace of
$\mathsf {M}_k$
a closed subspace of
![]() $\mathsf {M}$
and
$\mathsf {M}$
and
![]() ${\hbar }^n \mathsf {M}\cap \mathsf {M}_{\mathbb {Z}}={\hbar }^n\mathsf {M}_{\mathbb {Z}}$
for all
${\hbar }^n \mathsf {M}\cap \mathsf {M}_{\mathbb {Z}}={\hbar }^n\mathsf {M}_{\mathbb {Z}}$
for all
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
If, in addition,
![]() $\mathsf {M}$
has the structure of a topological algebra, then it is
$\mathsf {M}$
has the structure of a topological algebra, then it is
![]() $\mathbb {Z}$
-graded if and only if the above conditions hold and
$\mathbb {Z}$
-graded if and only if the above conditions hold and
![]() $\mathsf {M}_{\mathbb {Z}}$
is a
$\mathsf {M}_{\mathbb {Z}}$
is a
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-subalgebra of
$\mathbb {C}[{\hbar }]$
-subalgebra of
![]() $\mathsf {M}$
.
$\mathsf {M}$
.
If
![]() $\mathsf {M}$
is a
$\mathsf {M}$
is a
![]() $\mathbb {Z}$
-graded topological module, then the kth component
$\mathbb {Z}$
-graded topological module, then the kth component
![]() $\mathsf {M}_k$
of
$\mathsf {M}_k$
of
![]() $\mathsf {M}_{\mathbb {Z}}$
from Lemma 2.4 is uniquely determined and recovered as the inverse limit
$\mathsf {M}_{\mathbb {Z}}$
from Lemma 2.4 is uniquely determined and recovered as the inverse limit
Moreover, one has
![]() $(\mathsf {M}/{\hbar }^n \mathsf {M})_k\cong \mathsf {M}_k/{\hbar }^n \mathsf {M}_{k-n}$
for all
$(\mathsf {M}/{\hbar }^n \mathsf {M})_k\cong \mathsf {M}_k/{\hbar }^n \mathsf {M}_{k-n}$
for all
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $k\in \mathbb {Z}$
.
$k\in \mathbb {Z}$
.
We further observe that, for each
![]() $k\in \mathbb {Z}$
, the system of linear projections
$k\in \mathbb {Z}$
, the system of linear projections
![]() $\pi _{n,k}:\mathsf {M}/{\hbar }^n\mathsf {M}\to (\mathsf {M}/{\hbar }^n\mathsf {M})_k$
gives rise to a projection
$\pi _{n,k}:\mathsf {M}/{\hbar }^n\mathsf {M}\to (\mathsf {M}/{\hbar }^n\mathsf {M})_k$
gives rise to a projection
which restricts to the projection of
![]() $\mathsf {M}_{\mathbb {Z}}$
onto its kth homogeneous component. In particular, a
$\mathsf {M}_{\mathbb {Z}}$
onto its kth homogeneous component. In particular, a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear map
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear map
![]() between
between
![]() $\mathbb {Z}$
-graded topological modules is graded if and only if
$\mathbb {Z}$
-graded topological modules is graded if and only if
![]() $\pi _k^{\mathsf {N}}\circ \unicode{x3c4} =\unicode{x3c4} \circ \pi _k^{\mathsf {M}}$
for each
$\pi _k^{\mathsf {N}}\circ \unicode{x3c4} =\unicode{x3c4} \circ \pi _k^{\mathsf {M}}$
for each
![]() $k\in \mathbb {Z}$
.
$k\in \mathbb {Z}$
.
We conclude this preliminary subsection with two corollaries of the above discussion. The first shows that any topologically free
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module is of the form described above Lemma 2.4.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module is of the form described above Lemma 2.4.
Corollary 2.5 Suppose
![]() $\mathsf {M}$
is a
$\mathsf {M}$
is a
![]() $\mathbb {Z}$
-graded topologically free module over
$\mathbb {Z}$
-graded topologically free module over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, and let
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, and let
![]() $\mathsf {V}$
denote the
$\mathsf {V}$
denote the
![]() $\mathbb {Z}$
-graded complex vector space
$\mathbb {Z}$
-graded complex vector space
![]() $\mathsf {M}/{\hbar }\mathsf {M}=\bigoplus _{k\in \mathbb {Z}} \mathsf {M}_k/{\hbar } \mathsf {M}_{k-1}$
. Then
$\mathsf {M}/{\hbar }\mathsf {M}=\bigoplus _{k\in \mathbb {Z}} \mathsf {M}_k/{\hbar } \mathsf {M}_{k-1}$
. Then
as a
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module. In particular, one has
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module. In particular, one has
Proof This is a refinement of the elementary result, alluded to at the beginning of the section, that
![]() $\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as a
$\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module (see [Reference Kassel26, Proposition XVI.2.4], for instance). In more detail, an isomorphism of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module (see [Reference Kassel26, Proposition XVI.2.4], for instance). In more detail, an isomorphism of
![]() $\mathbb {Z}$
-graded topological modules
$\mathbb {Z}$
-graded topological modules
![]() $\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
is specified by choosing, for each
$\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
is specified by choosing, for each
![]() $k\in \mathbb {Z}$
, a complement
$k\in \mathbb {Z}$
, a complement
![]() $\mathsf {V}_k\subset \mathsf {M}_k$
to
$\mathsf {V}_k\subset \mathsf {M}_k$
to
![]() ${\hbar }\mathsf {M}_{k-1}$
in
${\hbar }\mathsf {M}_{k-1}$
in
![]() $\mathsf {M}_k$
:
$\mathsf {M}_k$
:
Setting
![]() $\mathsf {V}:=\bigoplus _{k\in \mathbb {Z}}\mathsf {V}_k\subset \mathsf {M}_{\mathbb {Z}}$
, we then have
$\mathsf {V}:=\bigoplus _{k\in \mathbb {Z}}\mathsf {V}_k\subset \mathsf {M}_{\mathbb {Z}}$
, we then have

where the third line is an identification of
![]() $\mathbb {Z}$
-graded modules. Here, we note that the second line follows from the definition of
$\mathbb {Z}$
-graded modules. Here, we note that the second line follows from the definition of
![]() $\mathsf {V}_k$
and that
$\mathsf {V}_k$
and that
![]() $\mathsf {M}$
is a torsion-free
$\mathsf {M}$
is a torsion-free
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module. Taking inverse limits, one finds that
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module. Taking inverse limits, one finds that
![]() $\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as
$\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules.
Let us now shift our attention to the case where
![]() $\dot {\mathsf {M}}=\bigoplus _{k\in \mathbb {N}} \dot {\mathsf {M}}_k$
is an
$\dot {\mathsf {M}}=\bigoplus _{k\in \mathbb {N}} \dot {\mathsf {M}}_k$
is an
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-module. Any such module is automatically separated, and so embeds into its
$\mathbb {C}[{\hbar }]$
-module. Any such module is automatically separated, and so embeds into its
![]() ${\hbar }$
-adic completion
${\hbar }$
-adic completion
which is an
![]() $\mathbb {N}$
-graded topological
$\mathbb {N}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module. Moreover, if
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module. Moreover, if
![]() $\dot {\mathsf {M}}$
is a torsion-free
$\dot {\mathsf {M}}$
is a torsion-free
![]() $\mathbb {C}[{\hbar }]$
-module, then
$\mathbb {C}[{\hbar }]$
-module, then
![]() $\mathsf {M}$
is topologically free as a
$\mathsf {M}$
is topologically free as a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module. Since
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module. Since
![]() ${\dot {\mathsf {M}}}_{k-n}$
is trivial for
${\dot {\mathsf {M}}}_{k-n}$
is trivial for
![]() $n>k$
, the submodule
$n>k$
, the submodule
![]() $\mathsf {M}_k$
of
$\mathsf {M}_k$
of
![]() $\mathsf {M}$
(see (2.1)) coincides with
$\mathsf {M}$
(see (2.1)) coincides with
![]() ${\dot {\mathsf {M}}}_k$
and so, in the notation of Lemma 2.4, one has
${\dot {\mathsf {M}}}_k$
and so, in the notation of Lemma 2.4, one has
![]() $\dot {\mathsf {M}}=\mathsf {M}_{\mathbb {N}}$
. These observations, coupled with Corollary 2.5 and that
$\dot {\mathsf {M}}=\mathsf {M}_{\mathbb {N}}$
. These observations, coupled with Corollary 2.5 and that
![]() $\mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]_k=\mathsf {V}[{\hbar }]_k$
when
$\mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]_k=\mathsf {V}[{\hbar }]_k$
when
![]() $\mathsf {V}$
is
$\mathsf {V}$
is
![]() $\mathbb {N}$
-graded, yield the following.
$\mathbb {N}$
-graded, yield the following.
Corollary 2.6 Let
![]() $\dot {\mathsf {M}}$
be an
$\dot {\mathsf {M}}$
be an
![]() $\mathbb {N}$
-graded, torsion-free
$\mathbb {N}$
-graded, torsion-free
![]() $\mathbb {C}[{\hbar }]$
-module. Then
$\mathbb {C}[{\hbar }]$
-module. Then
![]() $\mathsf {M}$
is a topologically free
$\mathsf {M}$
is a topologically free
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module. Moreover, we have
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module. Moreover, we have
Consequently,
![]() $\dot {\mathsf {M}}$
coincides with
$\dot {\mathsf {M}}$
coincides with
![]() $\mathsf {M}_{\mathbb {N}}$
and there is an isomorphism of
$\mathsf {M}_{\mathbb {N}}$
and there is an isomorphism of
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-modules
$\mathbb {C}[{\hbar }]$
-modules
Note that if
![]() $\dot {\mathsf {M}}$
is an
$\dot {\mathsf {M}}$
is an
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-algebra or Hopf algebra, then
$\mathbb {C}[{\hbar }]$
-algebra or Hopf algebra, then
![]() $\mathsf {M}$
is automatically an
$\mathsf {M}$
is automatically an
![]() $\mathbb {N}$
-graded topological algebra or Hopf algebra, respectively.
$\mathbb {N}$
-graded topological algebra or Hopf algebra, respectively.
2.3 The restricted dual
For a given
![]() $\mathbb {Z}$
-graded complex vector space
$\mathbb {Z}$
-graded complex vector space
![]() $\mathsf {V}=\bigoplus _n \mathsf {V}_n$
, we let
$\mathsf {V}=\bigoplus _n \mathsf {V}_n$
, we let
![]() $\mathsf {V}^\star =\bigoplus _n (\mathsf {V}^\star )_n\subset \mathsf {V}^\ast $
denote the restricted, or graded, dual of
$\mathsf {V}^\star =\bigoplus _n (\mathsf {V}^\star )_n\subset \mathsf {V}^\ast $
denote the restricted, or graded, dual of
![]() $\mathsf {V}$
, where
$\mathsf {V}$
, where
and
![]() $\mathbb {C}$
is given the trivial grading with
$\mathbb {C}$
is given the trivial grading with
![]() $\mathbb {C}_0=\mathbb {C}$
and
$\mathbb {C}_0=\mathbb {C}$
and
![]() $\mathbb {C}_m=\{0\}$
for
$\mathbb {C}_m=\{0\}$
for
![]() $m\neq 0$
. One can similarly define the restricted dual
$m\neq 0$
. One can similarly define the restricted dual
![]() $\mathsf {M}^\star \subset \mathsf {M}^\ast $
in the category of
$\mathsf {M}^\star \subset \mathsf {M}^\ast $
in the category of
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules. In this subsection, we will recall some properties of this duality operation in the
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules. In this subsection, we will recall some properties of this duality operation in the
![]() $\mathbb {N}$
-graded setting which will be applied to construct the dual Yangian in Section 6.
$\mathbb {N}$
-graded setting which will be applied to construct the dual Yangian in Section 6.
Suppose that
![]() $\mathsf {M}$
is an
$\mathsf {M}$
is an
![]() $\mathbb {N}$
-graded, topological
$\mathbb {N}$
-graded, topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module with
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module with
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-submodule
$\mathbb {C}[{\hbar }]$
-submodule
![]() $\mathsf {M}_{\mathbb {N}}=\bigoplus _{k\in \mathbb {N}}\mathsf {M}_k$
as in Lemma 2.4. For each
$\mathsf {M}_{\mathbb {N}}=\bigoplus _{k\in \mathbb {N}}\mathsf {M}_k$
as in Lemma 2.4. For each
![]() $n\in \mathbb {N}$
, let
$n\in \mathbb {N}$
, let
![]() $\mathsf {J}_k$
denote the
$\mathsf {J}_k$
denote the
![]() ${\hbar }$
-adic completion of the ideal
${\hbar }$
-adic completion of the ideal
![]() $\bigoplus _{k\geq n}\mathsf {M}_k$
of
$\bigoplus _{k\geq n}\mathsf {M}_k$
of
![]() $\mathsf {M}_{\mathbb {N}}$
. The gradation topology on
$\mathsf {M}_{\mathbb {N}}$
. The gradation topology on
![]() $\mathsf {M}$
is the topology associated with the descending filtration
$\mathsf {M}$
is the topology associated with the descending filtration
Equipped with this terminology, we may make the following definition.
Definition 2.7 The restricted dual
![]() $\mathsf {M}^\star $
is defined to be the
$\mathsf {M}^\star $
is defined to be the
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-submodule of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-submodule of
![]() $\mathsf {M}^\ast $
consisting of those f which are continuous with respect to the gradation topology:
$\mathsf {M}^\ast $
consisting of those f which are continuous with respect to the gradation topology:
The restricted dual of any
![]() $\mathbb {N}$
-graded topological
$\mathbb {N}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module
![]() $\mathsf {M}$
is easily seen to be separated, complete, and torsion-free. Let us now see that it admits a
$\mathsf {M}$
is easily seen to be separated, complete, and torsion-free. Let us now see that it admits a
![]() $\mathbb {Z}$
-graded structure.
$\mathbb {Z}$
-graded structure.
For each
![]() $a\in \mathbb {Z}$
, let
$a\in \mathbb {Z}$
, let
![]() $\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}^a(\mathsf {M},\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])\subset \mathsf {M}^\star $
denote the (closed) subspace consisting of
$\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}^a(\mathsf {M},\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])\subset \mathsf {M}^\star $
denote the (closed) subspace consisting of
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphisms
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphisms
![]() $f:\mathsf {M}\to \mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
of degree a. Equivalently,
$f:\mathsf {M}\to \mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
of degree a. Equivalently,
Then the sum
![]() $\sum _{a\in \mathbb {Z}}\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}^a(\mathsf {M},\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])$
is direct and the space
$\sum _{a\in \mathbb {Z}}\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}^a(\mathsf {M},\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])$
is direct and the space
is a
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-submodule of
$\mathbb {C}[{\hbar }]$
-submodule of
![]() $\mathsf {M}^\star $
.
$\mathsf {M}^\star $
.
Remark 2.8 Under the natural identification of
![]() $\mathsf {M}^\ast $
with
$\mathsf {M}^\ast $
with
![]() $\mathrm {Hom}_{\mathbb {C}[{\hbar }]}(\mathsf {M}_{\mathbb {N}},\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])$
, one has
$\mathrm {Hom}_{\mathbb {C}[{\hbar }]}(\mathsf {M}_{\mathbb {N}},\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])$
, one has
![]() $\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}^a(\mathsf {M},\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])\cong \mathrm {Hom}_{\mathbb {C}[{\hbar }]}^a(\mathsf {M}_{\mathbb {N}},\mathbb {C}[{\hbar }])$
and
$\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}^a(\mathsf {M},\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])\cong \mathrm {Hom}_{\mathbb {C}[{\hbar }]}^a(\mathsf {M}_{\mathbb {N}},\mathbb {C}[{\hbar }])$
and
![]() $(\mathsf {M}^\star )_{\mathbb {Z}}$
coincides with the graded dual
$(\mathsf {M}^\star )_{\mathbb {Z}}$
coincides with the graded dual
![]() $(\mathsf {M}_{\mathbb {N}})^\star \subset \mathrm {Hom}_{\mathbb {C}[{\hbar }]}(\mathsf {M}_{\mathbb {N}},\mathbb {C}[{\hbar }])$
of
$(\mathsf {M}_{\mathbb {N}})^\star \subset \mathrm {Hom}_{\mathbb {C}[{\hbar }]}(\mathsf {M}_{\mathbb {N}},\mathbb {C}[{\hbar }])$
of
![]() $\mathsf {M}_{\mathbb {N}}$
taken in the category of
$\mathsf {M}_{\mathbb {N}}$
taken in the category of
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-modules.
$\mathbb {C}[{\hbar }]$
-modules.
It is not difficult to prove that, for each
![]() $n\in \mathbb {N}$
, one has
$n\in \mathbb {N}$
, one has
Consequently,
![]() $\mathsf {M}^\star $
coincides with the
$\mathsf {M}^\star $
coincides with the
![]() ${\hbar }$
-adic completion of
${\hbar }$
-adic completion of
![]() $(\mathsf {M}^\star )_{\mathbb {Z}}$
and, by Lemma 2.4, is a
$(\mathsf {M}^\star )_{\mathbb {Z}}$
and, by Lemma 2.4, is a
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module. We note that, although Definition 2.7 is strictly for an
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module. We note that, although Definition 2.7 is strictly for an
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module
![]() $\mathsf {M}$
, one can define the restricted dual in the
$\mathsf {M}$
, one can define the restricted dual in the
![]() $\mathbb {Z}$
-graded setting precisely as the
$\mathbb {Z}$
-graded setting precisely as the
![]() ${\hbar }$
-adic completion of the space
${\hbar }$
-adic completion of the space
![]() $(\mathsf {M}^\star )_{\mathbb {Z}}$
.
$(\mathsf {M}^\star )_{\mathbb {Z}}$
.
If
![]() $\mathsf {M}$
is itself topologically free with
$\mathsf {M}$
is itself topologically free with
![]() $\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
for a graded vector space
$\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
for a graded vector space
![]() ${\mathsf {V}=\bigoplus _{k\in \mathbb {N}}\mathsf {V}_n}$
, then the natural homomorphism
${\mathsf {V}=\bigoplus _{k\in \mathbb {N}}\mathsf {V}_n}$
, then the natural homomorphism
![]() $\mathsf {M}^\star /{\hbar } \mathsf {M}^\star \to \mathsf {V}^\star $
is an isomorphism of graded vector spaces. As
$\mathsf {M}^\star /{\hbar } \mathsf {M}^\star \to \mathsf {V}^\star $
is an isomorphism of graded vector spaces. As
![]() $\mathsf {M}^\star $
is topologically free, Corollary 2.5 yields the following.
$\mathsf {M}^\star $
is topologically free, Corollary 2.5 yields the following.
Corollary 2.9 Suppose that
![]() $\mathsf {M}$
is a topologically free
$\mathsf {M}$
is a topologically free
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module with
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module with
![]() $\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
for a graded vector space
$\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
for a graded vector space
![]() $\mathsf {V}=\bigoplus _{k\in \mathbb {N}}\mathsf {V}_k$
. Then
$\mathsf {V}=\bigoplus _{k\in \mathbb {N}}\mathsf {V}_k$
. Then
![]() $\mathsf {M}^\star $
is isomorphic to
$\mathsf {M}^\star $
is isomorphic to
![]() $\mathsf {V}^\star [\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as a
$\mathsf {V}^\star [\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as a
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module.
We shall say that a topologically free
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module is of finite type if the graded components
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module is of finite type if the graded components
![]() $\mathsf {V}_k$
of
$\mathsf {V}_k$
of
![]() $\mathsf {V}\cong \mathsf {M}/{\hbar }\mathsf {M}$
from the above corollary are all finite-dimensional complex vector spaces.
$\mathsf {V}\cong \mathsf {M}/{\hbar }\mathsf {M}$
from the above corollary are all finite-dimensional complex vector spaces.
Now suppose that
![]() $\mathsf {H}$
is an
$\mathsf {H}$
is an
![]() $\mathbb {N}$
-graded topological Hopf algebra with coproduct
$\mathbb {N}$
-graded topological Hopf algebra with coproduct
![]() $\Delta $
, counit
$\Delta $
, counit
![]() $\varepsilon $
, antipode S, product m, and unit
$\varepsilon $
, antipode S, product m, and unit
![]() $\iota $
. Since these are all
$\iota $
. Since these are all
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphisms and
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphisms and
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]^\star \cong \mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, taking transposes yields
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]^\star \cong \mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, taking transposes yields
![]() $\mathbb {Z}$
-graded maps
$\mathbb {Z}$
-graded maps
 $$ \begin{gather*} \Delta^t: (\mathsf{H}\, \widehat{\otimes}\,\mathsf{H})^\star\to \mathsf{H}^\star,\quad \varepsilon^t: \mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt]\to \mathsf{H}^\star, \quad S^t:\mathsf{H}^\star\to \mathsf{H}^\star \\ m^t:\mathsf{H}^\star\to(\mathsf{H}\, \widehat{\otimes}\,\mathsf{H})^\star, \quad \iota^t: \mathsf{H}^\star \to \mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt] \end{gather*} $$
$$ \begin{gather*} \Delta^t: (\mathsf{H}\, \widehat{\otimes}\,\mathsf{H})^\star\to \mathsf{H}^\star,\quad \varepsilon^t: \mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt]\to \mathsf{H}^\star, \quad S^t:\mathsf{H}^\star\to \mathsf{H}^\star \\ m^t:\mathsf{H}^\star\to(\mathsf{H}\, \widehat{\otimes}\,\mathsf{H})^\star, \quad \iota^t: \mathsf{H}^\star \to \mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt] \end{gather*} $$
which formally satisfy the axioms of a Hopf algebra. In particular,
![]() $\mathsf {H}^\star $
is a topological
$\mathsf {H}^\star $
is a topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra with unit
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra with unit
![]() $\varepsilon ^t$
and product given by restricting
$\varepsilon ^t$
and product given by restricting
![]() $\Delta ^t$
. It is not, in general, a topological coalgebra (or Hopf algebra) as
$\Delta ^t$
. It is not, in general, a topological coalgebra (or Hopf algebra) as
![]() $m^t$
does not necessarily have image in
$m^t$
does not necessarily have image in
![]() $\mathsf {H}^\star \, \widehat {\otimes }\,\mathsf {H}^\star $
. However, this is the case when
$\mathsf {H}^\star \, \widehat {\otimes }\,\mathsf {H}^\star $
. However, this is the case when
![]() $\mathsf {H}$
is of finite type, as we now explain.
$\mathsf {H}$
is of finite type, as we now explain.
In general, for any two
![]() $\mathbb {N}$
-graded topological
$\mathbb {N}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
![]() $\mathsf {M}$
and
$\mathsf {M}$
and
![]() $\mathsf {N}$
, there is a canonical injective homomorphism of
$\mathsf {N}$
, there is a canonical injective homomorphism of
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
If
![]() $\mathsf {M}$
and
$\mathsf {M}$
and
![]() $\mathsf {N}$
are topologically free with
$\mathsf {N}$
are topologically free with
![]() $\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
and
$\mathsf {M}\cong \mathsf {V}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
and
![]() $\mathsf {N}\cong \mathsf {W}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, then the semiclassical limit of
$\mathsf {N}\cong \mathsf {W}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, then the semiclassical limit of
![]() $\unicode{x3b3} $
is the natural inclusion
$\unicode{x3b3} $
is the natural inclusion
![]() $\mathsf {V}^\star \otimes _{\mathbb {C}} \mathsf {W}^\star \hookrightarrow (\mathsf {V}\otimes _{\mathbb {C}} \mathsf {W})^\star $
which is an isomorphism provided the graded components of
$\mathsf {V}^\star \otimes _{\mathbb {C}} \mathsf {W}^\star \hookrightarrow (\mathsf {V}\otimes _{\mathbb {C}} \mathsf {W})^\star $
which is an isomorphism provided the graded components of
![]() $\mathsf {V}$
or
$\mathsf {V}$
or
![]() $\mathsf {W}$
are all finite-dimensional. This observation, together with Lemma 2.1, implies the following proposition.
$\mathsf {W}$
are all finite-dimensional. This observation, together with Lemma 2.1, implies the following proposition.
Proposition 2.10 Let
![]() $\mathsf {M}$
and
$\mathsf {M}$
and
![]() $\mathsf {N}$
be topologically free,
$\mathsf {N}$
be topologically free,
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules and suppose that either
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules and suppose that either
![]() $\mathsf {M}$
or
$\mathsf {M}$
or
![]() $\mathsf {N}$
is of finite type. Then
$\mathsf {N}$
is of finite type. Then
![]() $\unicode{x3b3} $
is an isomorphism of
$\unicode{x3b3} $
is an isomorphism of
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
Consequently, if
![]() $\mathsf {H}$
is a topologically free
$\mathsf {H}$
is a topologically free
![]() $\mathbb {N}$
-graded Hopf algebra of finite type, then
$\mathbb {N}$
-graded Hopf algebra of finite type, then
![]() $\mathsf {H}^\star $
is a
$\mathsf {H}^\star $
is a
![]() $\mathbb {Z}$
-graded topological Hopf algebra over
$\mathbb {Z}$
-graded topological Hopf algebra over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
.
Remark 2.11 Henceforth, we shall simply write
![]() $\otimes $
for the topological tensor product
$\otimes $
for the topological tensor product
![]() $\widehat {\otimes }$
. More generally, the use of the symbol
$\widehat {\otimes }$
. More generally, the use of the symbol
![]() $\otimes $
will always be clear from context and will be clarified should any ambiguity arise.
$\otimes $
will always be clear from context and will be clarified should any ambiguity arise.
2.4 Homogeneous quantizations
Let us now recall some basic constructions from the theory of quantum groups, adapted to the graded setting.
A topological Hopf algebra
![]() $\mathsf {H}$
over
$\mathsf {H}$
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
is called a quantized enveloping algebra if it is a flat deformation of the universal enveloping algebra
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
is called a quantized enveloping algebra if it is a flat deformation of the universal enveloping algebra
![]() $U(\mathfrak {b})$
of a complex Lie algebra
$U(\mathfrak {b})$
of a complex Lie algebra
![]() $\mathfrak {b}$
as a Hopf algebra. Equivalently:
$\mathfrak {b}$
as a Hopf algebra. Equivalently:
-
• The semiclassical limit
 $\mathsf {H}/{\hbar }\mathsf {H}$
of
$\mathsf {H}/{\hbar }\mathsf {H}$
of
 $\mathsf {H}$
is isomorphic to
$\mathsf {H}$
is isomorphic to
 $U(\mathfrak {b})$
as a Hopf algebra.
$U(\mathfrak {b})$
as a Hopf algebra. -
•
 $\mathsf {H}$
is topologically free, and thus isomorphic to
$\mathsf {H}$
is topologically free, and thus isomorphic to
 $U(\mathfrak {b})[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as a
$U(\mathfrak {b})[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as a
 $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module.
If
![]() $\mathsf {H}=U_{\hbar }\mathfrak {b}$
is a quantized enveloping algebra with semiclassical limit
$\mathsf {H}=U_{\hbar }\mathfrak {b}$
is a quantized enveloping algebra with semiclassical limit
![]() $U(\mathfrak {b})$
, then
$U(\mathfrak {b})$
, then
![]() $\mathfrak {b}$
inherits from
$\mathfrak {b}$
inherits from
![]() $U_{\hbar }\mathfrak {b}$
the structure of a Lie bialgebra with cocommutator
$U_{\hbar }\mathfrak {b}$
the structure of a Lie bialgebra with cocommutator
![]() $\delta _{\mathfrak {b}}:\mathfrak {b}\to \mathfrak {b}\wedge \mathfrak {b}\subset U(\mathfrak {b})^{\otimes 2}$
given by the formula
$\delta _{\mathfrak {b}}:\mathfrak {b}\to \mathfrak {b}\wedge \mathfrak {b}\subset U(\mathfrak {b})^{\otimes 2}$
given by the formula
where
![]() $\dot {x}\in U_{\hbar }\mathfrak {b}$
is any lift of x. We refer the reader to Propositions 6.2.3 and 6.2.7 of [Reference Chari and Pressley4] for a detailed discussion of this point.
$\dot {x}\in U_{\hbar }\mathfrak {b}$
is any lift of x. We refer the reader to Propositions 6.2.3 and 6.2.7 of [Reference Chari and Pressley4] for a detailed discussion of this point.
Conversely, if
![]() $(\mathfrak {b},\delta _{\mathfrak {b}})$
is a Lie bialgebra, then a quantization of
$(\mathfrak {b},\delta _{\mathfrak {b}})$
is a Lie bialgebra, then a quantization of
![]() $(\mathfrak {b},\delta _{\mathfrak {b}})$
is a quantized enveloping algebra
$(\mathfrak {b},\delta _{\mathfrak {b}})$
is a quantized enveloping algebra
![]() $U_{\hbar }\mathfrak {b}$
with semiclassical limit
$U_{\hbar }\mathfrak {b}$
with semiclassical limit
![]() $U(\mathfrak {b})$
, such that
$U(\mathfrak {b})$
, such that
![]() $\delta _{\mathfrak {b}}$
coincides with the cocommutator (2.2).
$\delta _{\mathfrak {b}}$
coincides with the cocommutator (2.2).
Now let us shift our attention to the graded setting. In what follows, we will say that a Lie bialgebra
![]() $(\mathfrak {b},\delta _{\mathfrak {b}})$
is
$(\mathfrak {b},\delta _{\mathfrak {b}})$
is
![]() $\mathbb {Z}$
-graded if
$\mathbb {Z}$
-graded if
![]() $\mathfrak {b}=\bigoplus _{k\in \mathbb {Z}}\mathfrak {b}_k$
is
$\mathfrak {b}=\bigoplus _{k\in \mathbb {Z}}\mathfrak {b}_k$
is
![]() $\mathbb {Z}$
-graded as a Lie algebra, and the cocommutator
$\mathbb {Z}$
-graded as a Lie algebra, and the cocommutator
![]() $\delta _{\mathfrak {b}}$
is a graded linear map of degree d, for some
$\delta _{\mathfrak {b}}$
is a graded linear map of degree d, for some
![]() $d\in \mathbb {Z}$
. That is,
$d\in \mathbb {Z}$
. That is,
![]() $\delta _{\mathfrak {b}}\in \mathrm {Hom}_{\mathbb {C}}^d(\mathfrak {b},{\mathfrak {b}}^{\otimes 2})$
.
$\delta _{\mathfrak {b}}\in \mathrm {Hom}_{\mathbb {C}}^d(\mathfrak {b},{\mathfrak {b}}^{\otimes 2})$
.
Definition 2.12 Let
![]() $\mathfrak {b}$
be a
$\mathfrak {b}$
be a
![]() $\mathbb {Z}$
-graded complex Lie bialgebra with cocommutator
$\mathbb {Z}$
-graded complex Lie bialgebra with cocommutator
![]() $\delta _{\mathfrak {b}}$
. Then a homogeneous quantization of
$\delta _{\mathfrak {b}}$
. Then a homogeneous quantization of
![]() $(\mathfrak {b},\delta _{\mathfrak {b}})$
is a topological Hopf algebra
$(\mathfrak {b},\delta _{\mathfrak {b}})$
is a topological Hopf algebra
![]() $U_{\hbar }\mathfrak {b}$
satisfying:
$U_{\hbar }\mathfrak {b}$
satisfying:
-
(1)
 $U_{\hbar }\mathfrak {b}$
is a quantization of
$U_{\hbar }\mathfrak {b}$
is a quantization of
 $(\mathfrak {b},\delta _{\mathfrak {b}})$
.
$(\mathfrak {b},\delta _{\mathfrak {b}})$
. -
(2)
 $U_{\hbar }\mathfrak {b}$
is
$U_{\hbar }\mathfrak {b}$
is
 $\mathbb {Z}$
-graded as a topological Hopf algebra, and the natural inclusion is a
$\mathbb {Z}$
-graded as a topological Hopf algebra, and the natural inclusion is a $$ \begin{align*} \mathfrak{b}\hookrightarrow U(\mathfrak{b})\cong U_{\hbar}\mathfrak{b}/{\hbar} U_{\hbar}\mathfrak{b} \end{align*} $$
$$ \begin{align*} \mathfrak{b}\hookrightarrow U(\mathfrak{b})\cong U_{\hbar}\mathfrak{b}/{\hbar} U_{\hbar}\mathfrak{b} \end{align*} $$
 $\mathbb {Z}$
-graded linear map.
$\mathbb {Z}$
-graded linear map.
Note that the last condition guarantees that the grading on
![]() $U(\mathfrak {b})$
inherited from
$U(\mathfrak {b})$
inherited from
![]() $U_{\hbar }\mathfrak {b}$
coincides with that induced by the Lie algebra grading on
$U_{\hbar }\mathfrak {b}$
coincides with that induced by the Lie algebra grading on
![]() $\mathfrak {b}$
. In addition, since the coproduct
$\mathfrak {b}$
. In addition, since the coproduct
![]() $\Delta $
is homogeneous of degree zero, (2.2) implies that the cocommutator
$\Delta $
is homogeneous of degree zero, (2.2) implies that the cocommutator
![]() $\delta _{\mathfrak {b}}$
must be of degree
$\delta _{\mathfrak {b}}$
must be of degree
![]() $d=-1$
.
$d=-1$
.
We shall employ similar terminology to the above in the
![]() $\mathbb {N}$
-graded setting over
$\mathbb {N}$
-graded setting over
![]() $\mathbb {C}[{\hbar }]$
. Namely, if
$\mathbb {C}[{\hbar }]$
. Namely, if
![]() $(\mathfrak {b},\delta _{\mathfrak {b}})$
is an
$(\mathfrak {b},\delta _{\mathfrak {b}})$
is an
![]() $\mathbb {N}$
-graded Lie bialgebra, then a homogeneous quantization of
$\mathbb {N}$
-graded Lie bialgebra, then a homogeneous quantization of
![]() $(\mathfrak {b},\delta _{\mathfrak {b}})$
over
$(\mathfrak {b},\delta _{\mathfrak {b}})$
over
![]() $\mathbb {C}[{\hbar }]$
is a space
$\mathbb {C}[{\hbar }]$
is a space
![]() $ {U}_{\hbar }\mathfrak {b}$
such that:
$ {U}_{\hbar }\mathfrak {b}$
such that:
-
(1)
 $ {U}_{\hbar }\mathfrak {b}$
is an
$ {U}_{\hbar }\mathfrak {b}$
is an
 $\mathbb {N}$
-graded torsion-free Hopf algebra over
$\mathbb {N}$
-graded torsion-free Hopf algebra over
 $\mathbb {C}[{\hbar }]$
.
$\mathbb {C}[{\hbar }]$
. -
(2) The semiclassical limit
 $ {U}_{\hbar }\mathfrak {b}/{\hbar } {U}_{\hbar }\mathfrak {b}$
is isomorphic to
$ {U}_{\hbar }\mathfrak {b}/{\hbar } {U}_{\hbar }\mathfrak {b}$
is isomorphic to
 $U(\mathfrak {b})$
as a graded Hopf algebra, with the cocommutator
$U(\mathfrak {b})$
as a graded Hopf algebra, with the cocommutator
 $\delta _{\mathfrak {b}}$
given by (2.2).
$\delta _{\mathfrak {b}}$
given by (2.2).
Note that, by Corollary 2.6, such a quantization
![]() $ {U}_{\hbar }\mathfrak {b}$
is isomorphic to
$ {U}_{\hbar }\mathfrak {b}$
is isomorphic to
![]() $U(\mathfrak {b})[{\hbar }]$
as an
$U(\mathfrak {b})[{\hbar }]$
as an
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-module, and its
$\mathbb {C}[{\hbar }]$
-module, and its
![]() ${\hbar }$
-adic completion is a homogeneous quantization of
${\hbar }$
-adic completion is a homogeneous quantization of
![]() $\mathfrak {b}$
over
$\mathfrak {b}$
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
.
2.5 The Yangian Manin triple
The most well-known, nontrivial, example of a homogeneous quantization is the Yangian
![]() $Y_{\hbar }\mathfrak {g}$
associated with an arbitrary simple Lie algebra
$Y_{\hbar }\mathfrak {g}$
associated with an arbitrary simple Lie algebra
![]() $\mathfrak {g}$
over the complex numbers. In this article, we shall encounter two other, closely related, examples: the dual Yangian
$\mathfrak {g}$
over the complex numbers. In this article, we shall encounter two other, closely related, examples: the dual Yangian
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
and the Yangian double
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
and the Yangian double
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
. Collectively, these three quantum groups arise as a quantization of a restricted Manin triple structure on
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
. Collectively, these three quantum groups arise as a quantization of a restricted Manin triple structure on
![]() $(\mathfrak {t},{\mathfrak {t}}_{\scriptscriptstyle {+}},{\mathfrak {t}}_{\scriptscriptstyle {-}})$
, where
$(\mathfrak {t},{\mathfrak {t}}_{\scriptscriptstyle {+}},{\mathfrak {t}}_{\scriptscriptstyle {-}})$
, where
In this section, we briefly recall how this structure is defined.
The Lie algebra
![]() $\mathfrak {t}=\mathfrak {g}[t^{\pm 1}]$
comes equipped with a nondegenerate, invariant bilinear form
$\mathfrak {t}=\mathfrak {g}[t^{\pm 1}]$
comes equipped with a nondegenerate, invariant bilinear form
![]() $\langle \,,\,\rangle :\mathfrak {t}\otimes \mathfrak {t}\to \mathbb {C}$
given by
$\langle \,,\,\rangle :\mathfrak {t}\otimes \mathfrak {t}\to \mathbb {C}$
given by
where
![]() $(\,,\,)$
is a fixed symmetric, invariant, and nondegenerate bilinear form on
$(\,,\,)$
is a fixed symmetric, invariant, and nondegenerate bilinear form on
![]() $\mathfrak {g}$
, which has been extended to a
$\mathfrak {g}$
, which has been extended to a
![]() $\mathbb {C}[t^{\pm 1}]$
-valued bilinear form on
$\mathbb {C}[t^{\pm 1}]$
-valued bilinear form on
![]() $\mathfrak {t}$
by
$\mathfrak {t}$
by
![]() $\mathbb {C}[t^{\pm 1}]$
-linearity. The above form is a degree
$\mathbb {C}[t^{\pm 1}]$
-linearity. The above form is a degree
![]() $1$
element of the restricted dual
$1$
element of the restricted dual
![]() $(\mathfrak {t}\otimes \mathfrak {t})^\star $
, as defined in the beginning of Section 2.3. Namely, it vanishes on
$(\mathfrak {t}\otimes \mathfrak {t})^\star $
, as defined in the beginning of Section 2.3. Namely, it vanishes on
for any
![]() $k\neq -1$
, and restricts to a nondegenerate pairing
$k\neq -1$
, and restricts to a nondegenerate pairing
![]() ${\mathfrak {t}}_a\otimes {\mathfrak {t}}_{-a-1}\to \mathbb {C}$
for any
${\mathfrak {t}}_a\otimes {\mathfrak {t}}_{-a-1}\to \mathbb {C}$
for any
![]() $a\in \mathbb {Z}$
. Moreover, one has the polarization
$a\in \mathbb {Z}$
. Moreover, one has the polarization
with
![]() ${\mathfrak {t}}_{\scriptscriptstyle {+}}$
and
${\mathfrak {t}}_{\scriptscriptstyle {+}}$
and
![]() ${\mathfrak {t}}_{\scriptscriptstyle {-}}$
isotropic, graded Lie subalgebras of
${\mathfrak {t}}_{\scriptscriptstyle {-}}$
isotropic, graded Lie subalgebras of
![]() $\mathfrak {t}$
, with gradings concentrated in nonnegative and nonpositive degrees, respectively. Said in fewer words, this collection of data gives rise to a restricted Manin triple
$\mathfrak {t}$
, with gradings concentrated in nonnegative and nonpositive degrees, respectively. Said in fewer words, this collection of data gives rise to a restricted Manin triple
![]() $(\mathfrak {t},{\mathfrak {t}}_{\scriptscriptstyle {+}},{\mathfrak {t}}_{\scriptscriptstyle {-}})$
(see Sections 5.2 and 5.3 of [Reference Appel and Toledano Laredo2]).
$(\mathfrak {t},{\mathfrak {t}}_{\scriptscriptstyle {+}},{\mathfrak {t}}_{\scriptscriptstyle {-}})$
(see Sections 5.2 and 5.3 of [Reference Appel and Toledano Laredo2]).
Since each homogeneous component
![]() ${\mathfrak {t}}_k$
of
${\mathfrak {t}}_k$
of
![]() $\mathfrak {t}$
is finite-dimensional, there are dual Lie bialgebra structures on
$\mathfrak {t}$
is finite-dimensional, there are dual Lie bialgebra structures on
![]() ${\mathfrak {t}}_{\scriptscriptstyle {+}}$
and
${\mathfrak {t}}_{\scriptscriptstyle {+}}$
and
![]() ${\mathfrak {t}}_{\scriptscriptstyle {-}}$
, obtained as follows. The residue form (2.3) yields isomorphisms of graded vector spaces
${\mathfrak {t}}_{\scriptscriptstyle {-}}$
, obtained as follows. The residue form (2.3) yields isomorphisms of graded vector spaces
which are homogeneous of degree
![]() $1$
:
$1$
:
![]() $\mathsf {Res}_{\pm }({\mathfrak {t}}_{{\scriptscriptstyle \pm },n})=(\mathfrak {t}^\star _{\scriptscriptstyle \mp })_{n+1}$
for all
$\mathsf {Res}_{\pm }({\mathfrak {t}}_{{\scriptscriptstyle \pm },n})=(\mathfrak {t}^\star _{\scriptscriptstyle \mp })_{n+1}$
for all
![]() $n\in \mathbb {Z}$
. Dualizing Lie brackets then gives rise to honest, degree
$n\in \mathbb {Z}$
. Dualizing Lie brackets then gives rise to honest, degree
![]() $-1$
, Lie bialgebra cobrackets
$-1$
, Lie bialgebra cobrackets
Observe that the Casimir tensor
![]() $\Omega _{\mathfrak {g}}\in (\mathfrak {g}\otimes \mathfrak {g})^{\mathfrak {g}}$
satisfies
$\Omega _{\mathfrak {g}}\in (\mathfrak {g}\otimes \mathfrak {g})^{\mathfrak {g}}$
satisfies
where
![]() $(,)_{\mathfrak {g}\otimes \mathfrak {g}}=(,)\otimes (,)\circ (2\,3):\mathfrak {g}\otimes \mathfrak {g}\otimes \mathfrak {g}\otimes \mathfrak {g}\to \mathbb {C}$
. It follows readily from this observation and the definition of
$(,)_{\mathfrak {g}\otimes \mathfrak {g}}=(,)\otimes (,)\circ (2\,3):\mathfrak {g}\otimes \mathfrak {g}\otimes \mathfrak {g}\otimes \mathfrak {g}\to \mathbb {C}$
. It follows readily from this observation and the definition of
![]() $\mathsf {Res}_\pm $
that
$\mathsf {Res}_\pm $
that
![]() $\delta _{\scriptscriptstyle +}$
and
$\delta _{\scriptscriptstyle +}$
and
![]() $\delta _{\scriptscriptstyle -}$
are given explicitly on each graded component by
$\delta _{\scriptscriptstyle -}$
are given explicitly on each graded component by
 $$ \begin{gather*} \delta_{\scriptscriptstyle +}(xt^k)=\sum_{a+b=k-1}\![x\otimes 1,\Omega_{\mathfrak{g}}]t^as^{b}\in \mathfrak{g}[t]\otimes \mathfrak{g}[s]={\mathfrak{t}}_{\scriptscriptstyle{+}}\otimes {\mathfrak{t}}_{\scriptscriptstyle{+}},\\ \delta_{\scriptscriptstyle -}(xt^{-k-1})=\sum_{a+b=k}[x\otimes 1,\Omega_{\mathfrak{g}}]t^{-a-1}s^{-b-1}\in t^{-1}\mathfrak{g}[t^{-1}]\otimes s^{-1}\mathfrak{g}[s^{-1}]={\mathfrak{t}}_{\scriptscriptstyle{-}}\otimes {\mathfrak{t}}_{\scriptscriptstyle{-}}, \end{gather*} $$
$$ \begin{gather*} \delta_{\scriptscriptstyle +}(xt^k)=\sum_{a+b=k-1}\![x\otimes 1,\Omega_{\mathfrak{g}}]t^as^{b}\in \mathfrak{g}[t]\otimes \mathfrak{g}[s]={\mathfrak{t}}_{\scriptscriptstyle{+}}\otimes {\mathfrak{t}}_{\scriptscriptstyle{+}},\\ \delta_{\scriptscriptstyle -}(xt^{-k-1})=\sum_{a+b=k}[x\otimes 1,\Omega_{\mathfrak{g}}]t^{-a-1}s^{-b-1}\in t^{-1}\mathfrak{g}[t^{-1}]\otimes s^{-1}\mathfrak{g}[s^{-1}]={\mathfrak{t}}_{\scriptscriptstyle{-}}\otimes {\mathfrak{t}}_{\scriptscriptstyle{-}}, \end{gather*} $$
where we have used the natural identification of
![]() $(\mathfrak {g}\otimes \mathfrak {g})[t^{\pm 1},s^{\pm 1}]$
with
$(\mathfrak {g}\otimes \mathfrak {g})[t^{\pm 1},s^{\pm 1}]$
with
![]() $\mathfrak {g}[t^{\pm 1}]\otimes \mathfrak {g}[s^{\pm 1}]$
, and
$\mathfrak {g}[t^{\pm 1}]\otimes \mathfrak {g}[s^{\pm 1}]$
, and
![]() $a,b$
take values in
$a,b$
take values in
![]() $\mathbb {N}$
. Since
$\mathbb {N}$
. Since
 $$ \begin{align*} (z-w)\sum_{a=0}^kz^aw^{k-a}=z^{k+1}-w^{k+1}, \end{align*} $$
$$ \begin{align*} (z-w)\sum_{a=0}^kz^aw^{k-a}=z^{k+1}-w^{k+1}, \end{align*} $$
the linear map ![]() is given by the formula
is given by the formula
and defines a Lie bialgebra structure on the Lie algebra
![]() $\mathfrak {t}$
such that
$\mathfrak {t}$
such that
![]() $({\mathfrak {t}}_{\scriptscriptstyle {+}},\delta _{\scriptscriptstyle +})$
and
$({\mathfrak {t}}_{\scriptscriptstyle {+}},\delta _{\scriptscriptstyle +})$
and
![]() $({\mathfrak {t}}_{\scriptscriptstyle {-}}, -\delta _{\scriptscriptstyle -})$
are Lie sub-bialgebras. This construction identifies
$({\mathfrak {t}}_{\scriptscriptstyle {-}}, -\delta _{\scriptscriptstyle -})$
are Lie sub-bialgebras. This construction identifies
![]() $\mathfrak {t}$
with the restricted Drinfeld double
$\mathfrak {t}$
with the restricted Drinfeld double
![]() $D({\mathfrak {t}}_{\scriptscriptstyle {+}})$
of the
$D({\mathfrak {t}}_{\scriptscriptstyle {+}})$
of the
![]() $\mathbb {N}$
-graded Lie bialgebra
$\mathbb {N}$
-graded Lie bialgebra
![]() ${\mathfrak {t}}_{\scriptscriptstyle {+}}$
, as defined in [Reference Appel and Toledano Laredo2, Section 5.4], for instance.
${\mathfrak {t}}_{\scriptscriptstyle {+}}$
, as defined in [Reference Appel and Toledano Laredo2, Section 5.4], for instance.
3 The Yangian revisited
3.1 The Lie algebra
 $\mathfrak {g}$
$\mathfrak {g}$
We henceforth fix
![]() $\mathfrak {g}$
to be a finite-dimensional simple Lie algebra over the complex numbers, with invariant form
$\mathfrak {g}$
to be a finite-dimensional simple Lie algebra over the complex numbers, with invariant form
![]() $(\,,\,)$
as in Section 2.5. Let
$(\,,\,)$
as in Section 2.5. Let
![]() $\mathfrak {h}\subset \mathfrak {g}$
be a Cartan subalgebra,
$\mathfrak {h}\subset \mathfrak {g}$
be a Cartan subalgebra,
![]() $\{\alpha _i\}_{i\in \mathbf {I}}\subset \mathfrak {h}^\ast $
a basis of simple roots, and
$\{\alpha _i\}_{i\in \mathbf {I}}\subset \mathfrak {h}^\ast $
a basis of simple roots, and
![]() $\{\alpha _i^\vee \}_{i\in \mathbf {I}}$
the set of simple coroots, so that
$\{\alpha _i^\vee \}_{i\in \mathbf {I}}$
the set of simple coroots, so that
![]() $\alpha _j(\alpha _i^\vee )=a_{ij}=2(\alpha _i,\alpha _j)/(\alpha _i,\alpha _i)$
are the entries of the Cartan matrix
$\alpha _j(\alpha _i^\vee )=a_{ij}=2(\alpha _i,\alpha _j)/(\alpha _i,\alpha _i)$
are the entries of the Cartan matrix
![]() $\mathbf {A}=(a_{ij})_{i,j\in \mathbf {I}}$
of
$\mathbf {A}=(a_{ij})_{i,j\in \mathbf {I}}$
of
![]() $\mathfrak {g}$
. Let
$\mathfrak {g}$
. Let
![]() $\Delta ^+\subset \mathfrak {h}^\ast $
be the associated set of positive roots, and let
$\Delta ^+\subset \mathfrak {h}^\ast $
be the associated set of positive roots, and let
![]() $Q=\bigoplus _{i \in \mathbf {I}}\mathbb {Z}\alpha _i$
and
$Q=\bigoplus _{i \in \mathbf {I}}\mathbb {Z}\alpha _i$
and
![]() $Q_+=\bigoplus _{i\in \mathbf {I}} \mathbb {N}\alpha _i$
denote the root lattice and its positive cone, respectively, where we recall that
$Q_+=\bigoplus _{i\in \mathbf {I}} \mathbb {N}\alpha _i$
denote the root lattice and its positive cone, respectively, where we recall that
![]() $\mathbb {N}$
denotes the set of nonnegative integers. Set
$\mathbb {N}$
denotes the set of nonnegative integers. Set
We normalize
![]() $(\,,\,)$
, if necessary, so that the square length of a short root is
$(\,,\,)$
, if necessary, so that the square length of a short root is
![]() $2$
. In particular, we then have
$2$
. In particular, we then have
![]() $\{d_i\}_{i\in \mathbf {I}}\subset \{1,2,3\}$
. Let
$\{d_i\}_{i\in \mathbf {I}}\subset \{1,2,3\}$
. Let
![]() $\{e_i,f_i\}_{i\in \mathbf {I}}$
denote the Chevalley generators of
$\{e_i,f_i\}_{i\in \mathbf {I}}$
denote the Chevalley generators of
![]() $\mathfrak {g}$
, as in [Reference Kac24, Section 1.3], and set
$\mathfrak {g}$
, as in [Reference Kac24, Section 1.3], and set
These normalized generators satisfy
![]() $(x_i^+,x_i^-)=1$
and
$(x_i^+,x_i^-)=1$
and
![]() $h_i=[x_i^+,x_i^-]$
for all
$h_i=[x_i^+,x_i^-]$
for all
![]() $i\in \mathbf {I}$
.
$i\in \mathbf {I}$
.
3.2 The Yangian
We now recall the definition of the Yangian
![]() $Y_{\hbar }(\mathfrak {g})$
. Let
$Y_{\hbar }(\mathfrak {g})$
. Let
![]() $S_m$
denote the symmetric group on
$S_m$
denote the symmetric group on
![]() $\{1,\ldots ,m\}$
.
$\{1,\ldots ,m\}$
.
Definition 3.1 The Yangian
![]() $Y_{\hbar }(\mathfrak {g})$
is the unital associative
$Y_{\hbar }(\mathfrak {g})$
is the unital associative
![]() $\mathbb {C}[{\hbar }]$
-algebra generated by
$\mathbb {C}[{\hbar }]$
-algebra generated by
![]() $\{x_{ir}^\pm , h_{ir}\}_{i\in \mathbf {I},r\in \mathbb {N}}$
, subject to the following relations for
$\{x_{ir}^\pm , h_{ir}\}_{i\in \mathbf {I},r\in \mathbb {N}}$
, subject to the following relations for
![]() $i,j\in \mathbf {I}$
and
$i,j\in \mathbf {I}$
and
![]() $r,s\in \mathbb {N}$
:
$r,s\in \mathbb {N}$
:
where in the last relation
![]() $i\neq j$
,
$i\neq j$
,
![]() $m=1-a_{ij}$
, and
$m=1-a_{ij}$
, and
![]() $r_1,\ldots ,r_m\in \mathbb {N}$
.
$r_1,\ldots ,r_m\in \mathbb {N}$
.
The Yangian
![]() $Y_{\hbar }(\mathfrak {g})$
is an
$Y_{\hbar }(\mathfrak {g})$
is an
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-algebra, with grading
$\mathbb {C}[{\hbar }]$
-algebra, with grading
determined by
![]() $\deg x_{ir}^\pm =\deg h_{ir}=r$
for all
$\deg x_{ir}^\pm =\deg h_{ir}=r$
for all
![]() $i\in \mathbf {I}$
and
$i\in \mathbf {I}$
and
![]() $r\in \mathbb {N}$
. Moreover, Definition 6.1 is such that
$r\in \mathbb {N}$
. Moreover, Definition 6.1 is such that
![]() $Y_{\hbar }(\mathfrak {g})$
provides an
$Y_{\hbar }(\mathfrak {g})$
provides an
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-algebra deformation of the enveloping algebra
$\mathbb {C}[{\hbar }]$
-algebra deformation of the enveloping algebra
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
, where we recall that
$U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
, where we recall that
![]() ${\mathfrak {t}}_{\scriptscriptstyle {+}}=\mathfrak {g}[t]$
. Indeed, the identification
${\mathfrak {t}}_{\scriptscriptstyle {+}}=\mathfrak {g}[t]$
. Indeed, the identification
![]() $Y_{\hbar }(\mathfrak {g})/{\hbar } Y_{\hbar }(\mathfrak {g}) \cong U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
is induced by the graded algebra epimorphism
$Y_{\hbar }(\mathfrak {g})/{\hbar } Y_{\hbar }(\mathfrak {g}) \cong U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
is induced by the graded algebra epimorphism
![]() $q:Y_{\hbar }(\mathfrak {g})\twoheadrightarrow U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
given on generators by
$q:Y_{\hbar }(\mathfrak {g})\twoheadrightarrow U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
given on generators by
In addition, the relations (3.1)–(3.6) imply that the assignment
determines a
![]() $\mathbb {C}$
-algebra homomorphism
$\mathbb {C}$
-algebra homomorphism
![]() $U(\mathfrak {g})\to Y_{\hbar }(\mathfrak {g})$
, which is injective as its composition with q is the identity map
$U(\mathfrak {g})\to Y_{\hbar }(\mathfrak {g})$
, which is injective as its composition with q is the identity map
![]() $\mathbf {1}_{U(\mathfrak {g})}$
on
$\mathbf {1}_{U(\mathfrak {g})}$
on
![]() $U(\mathfrak {g})$
. Henceforth, we shall identify
$U(\mathfrak {g})$
. Henceforth, we shall identify
![]() $\mathfrak {g}$
with its image in
$\mathfrak {g}$
with its image in
![]() $Y_{\hbar }(\mathfrak {g})$
without further comment.
$Y_{\hbar }(\mathfrak {g})$
without further comment.
To specify the standard Hopf algebra structure on
![]() $Y_{\hbar }(\mathfrak {g})$
, we first note that
$Y_{\hbar }(\mathfrak {g})$
, we first note that
![]() $Y_{\hbar }(\mathfrak {g})$
is generated as a
$Y_{\hbar }(\mathfrak {g})$
is generated as a
![]() $\mathbb {C}[{\hbar }]$
-algebra by the set
$\mathbb {C}[{\hbar }]$
-algebra by the set
![]() $\mathfrak {g}\cup \{t_{i1}\}_{i\in \mathbf {I}}\subset Y_{\hbar }(\mathfrak {g})$
, where
$\mathfrak {g}\cup \{t_{i1}\}_{i\in \mathbf {I}}\subset Y_{\hbar }(\mathfrak {g})$
, where
More precisely, for each
![]() $s>0$
,
$s>0$
,
![]() $x_{is}^\pm $
and
$x_{is}^\pm $
and
![]() $h_{i,s+1}$
are determined by the recursive formulas
$h_{i,s+1}$
are determined by the recursive formulas
Now let
![]() $\mathsf {r}\in \mathfrak {n}_-\otimes \mathfrak {n}_+$
denote the canonical tensor associated with the pairing
$\mathsf {r}\in \mathfrak {n}_-\otimes \mathfrak {n}_+$
denote the canonical tensor associated with the pairing
![]() $(\,,\,)|_{\mathfrak {n}_-\times \mathfrak {n}_+}$
, where
$(\,,\,)|_{\mathfrak {n}_-\times \mathfrak {n}_+}$
, where
![]() $\mathfrak {n}_\pm =\bigoplus _{\alpha \in \Delta ^+}{\mathfrak {g}}_{\pm \alpha }$
is the Lie subalgebra of
$\mathfrak {n}_\pm =\bigoplus _{\alpha \in \Delta ^+}{\mathfrak {g}}_{\pm \alpha }$
is the Lie subalgebra of
![]() $\mathfrak {g}$
generated by
$\mathfrak {g}$
generated by
![]() $\{x_i^\pm \}_{i\in \mathbf {I}}$
. Equivalently,
$\{x_i^\pm \}_{i\in \mathbf {I}}$
. Equivalently,
![]() $\mathsf {r}$
is the unique preimage of the identity map under the natural isomorphism
$\mathsf {r}$
is the unique preimage of the identity map under the natural isomorphism ![]() , determined by
, determined by
![]() $(\,,\,)|_{\mathfrak {n}_-\times \mathfrak {n}_+}$
. In addition, we set
$(\,,\,)|_{\mathfrak {n}_-\times \mathfrak {n}_+}$
. In addition, we set
If
![]() $x_\alpha ^\pm \in {\mathfrak {g}}_{\pm \alpha }$
are root vectors satisfying
$x_\alpha ^\pm \in {\mathfrak {g}}_{\pm \alpha }$
are root vectors satisfying
![]() $(x_\alpha ^+,x_\alpha ^-)=1$
, then one has the formulae
$(x_\alpha ^+,x_\alpha ^-)=1$
, then one has the formulae
The following proposition describes the Hopf algebra structure on
![]() $Y_{\hbar }(\mathfrak {g})$
, where
$Y_{\hbar }(\mathfrak {g})$
, where
![]() $m:Y_{\hbar }(\mathfrak {g})^{\otimes 2}\to Y_{\hbar }(\mathfrak {g})$
denote the multiplication map.
$m:Y_{\hbar }(\mathfrak {g})^{\otimes 2}\to Y_{\hbar }(\mathfrak {g})$
denote the multiplication map.
Proposition 3.2 The Yangian
![]() $Y_{\hbar }(\mathfrak {g})$
is an
$Y_{\hbar }(\mathfrak {g})$
is an
![]() $\mathbb {N}$
-graded Hopf algebra with counit
$\mathbb {N}$
-graded Hopf algebra with counit
![]() $\varepsilon $
, coproduct
$\varepsilon $
, coproduct
![]() $\Delta $
, and antipode S uniquely determined by the requirement that
$\Delta $
, and antipode S uniquely determined by the requirement that
![]() $\mathfrak {g}$
is primitive and that, for each
$\mathfrak {g}$
is primitive and that, for each
![]() $i\in \mathbf {I}$
, one has
$i\in \mathbf {I}$
, one has
In particular,
![]() $Y_{\hbar }(\mathfrak {g})$
is an
$Y_{\hbar }(\mathfrak {g})$
is an
![]() $\mathbb {N}$
-graded Hopf algebra deformation of
$\mathbb {N}$
-graded Hopf algebra deformation of
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
over
$U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
over
![]() $\mathbb {C}[{\hbar }]$
.
$\mathbb {C}[{\hbar }]$
.
The crux of the proof of this proposition lies in showing that
![]() $\Delta $
is an algebra homomorphism. Though this is a consequence of [Reference Drinfel’d6, Theorem 2] and [Reference Drinfel’d8, Theorem 1] (see also [Reference Guay, Regelskis and Wendlandt22, Theorem 2.6]), a complete proof has only recently appeared in [Reference Guay, Nakajima and Wendlandt21] (see Theorem 4.9 therein).
$\Delta $
is an algebra homomorphism. Though this is a consequence of [Reference Drinfel’d6, Theorem 2] and [Reference Drinfel’d8, Theorem 1] (see also [Reference Guay, Regelskis and Wendlandt22, Theorem 2.6]), a complete proof has only recently appeared in [Reference Guay, Nakajima and Wendlandt21] (see Theorem 4.9 therein).
The Yangian
![]() $Y_{\hbar }(\mathfrak {g})$
also admits a Q-grading compatible with the above
$Y_{\hbar }(\mathfrak {g})$
also admits a Q-grading compatible with the above
![]() $\mathbb {N}$
-grading; that is to say, it is
$\mathbb {N}$
-grading; that is to say, it is
![]() $\mathbb {N}\times Q$
-graded as a Hopf algebra. This Q-grading arises from the adjoint action of the Cartan subalgebra
$\mathbb {N}\times Q$
-graded as a Hopf algebra. This Q-grading arises from the adjoint action of the Cartan subalgebra
![]() $\mathfrak {h}\subset \mathfrak {g}$
on
$\mathfrak {h}\subset \mathfrak {g}$
on
![]() $Y_{\hbar }(\mathfrak {g})$
. Namely, one has
$Y_{\hbar }(\mathfrak {g})$
. Namely, one has
![]() $Y_{\hbar }(\mathfrak {g})=\bigoplus _{\beta \in Q}Y_{\hbar }(\mathfrak {g})_\beta $
, where
$Y_{\hbar }(\mathfrak {g})=\bigoplus _{\beta \in Q}Y_{\hbar }(\mathfrak {g})_\beta $
, where
![]() $Y_{\hbar }(\mathfrak {g})_\beta $
is just the
$Y_{\hbar }(\mathfrak {g})_\beta $
is just the
![]() $\beta $
-weight space
$\beta $
-weight space
3.3 Automorphisms
There are two families of (anti)automorphisms of
![]() $Y_{\hbar }(\mathfrak {g})$
which will play an especially pronounced role in this article: the shift automorphisms and the Chevalley involution. The former are a family
$Y_{\hbar }(\mathfrak {g})$
which will play an especially pronounced role in this article: the shift automorphisms and the Chevalley involution. The former are a family
![]() $\{\tau _c\}_{c\in \mathbb {C}}\subset \mathrm {Aut}(Y_{\hbar }(\mathfrak {g}))$
which give rise to an action of the additive group
$\{\tau _c\}_{c\in \mathbb {C}}\subset \mathrm {Aut}(Y_{\hbar }(\mathfrak {g}))$
which give rise to an action of the additive group
![]() $\mathbb {C}$
on
$\mathbb {C}$
on
![]() $Y_{\hbar }(\mathfrak {g})$
by Hopf algebra automorphisms. In more detail,
$Y_{\hbar }(\mathfrak {g})$
by Hopf algebra automorphisms. In more detail,
![]() $\tau _c$
is defined explicitly by
$\tau _c$
is defined explicitly by
where we have introduced the generating series
![]() $x_i^\pm (u)$
and
$x_i^\pm (u)$
and
![]() $h_i(u)$
in
$h_i(u)$
in
![]() $Y_{\hbar }(\mathfrak {g})[\kern-1.2pt\![u^{-1}]\!\kern-1.2pt]$
by
$Y_{\hbar }(\mathfrak {g})[\kern-1.2pt\![u^{-1}]\!\kern-1.2pt]$
by
Replacing c by a formal variable z in (3.7), one obtains an
![]() $\mathbb {N}$
-graded embedding
$\mathbb {N}$
-graded embedding
called the formal shift homomorphism, where
![]() $\deg z=1$
. Let us now turn to defining the Chevalley involution, beginning with the following lemma.
$\deg z=1$
. Let us now turn to defining the Chevalley involution, beginning with the following lemma.
Lemma 3.3 The assignments
![]() $\omega $
and
$\omega $
and
![]() $\varsigma $
defined by
$\varsigma $
defined by
 $$ \begin{gather*} \omega(x_i^\pm(u))=x_{i}^\mp(u), \quad \omega(h_i(u))=h_i(u),\\ \varsigma(x_i^\pm(u))=x_i^\pm(-u), \quad \varsigma(h_i(u))=h_i(-u), \end{gather*} $$
$$ \begin{gather*} \omega(x_i^\pm(u))=x_{i}^\mp(u), \quad \omega(h_i(u))=h_i(u),\\ \varsigma(x_i^\pm(u))=x_i^\pm(-u), \quad \varsigma(h_i(u))=h_i(-u), \end{gather*} $$
extend to commuting anti-involutions
![]() $\omega $
and
$\omega $
and
![]() $\varsigma $
of
$\varsigma $
of
![]() $Y_{\hbar }(\mathfrak {g})$
. Moreover,
$Y_{\hbar }(\mathfrak {g})$
. Moreover,
![]() $\omega $
and
$\omega $
and
![]() $\varsigma $
satisfy
$\varsigma $
satisfy

This result, which has appeared in various forms in the literature (for instance, [Reference Chari and Pressley3, Proposition 2.9]), is readily established using Definition 6.1 and the relations of Proposition 3.2. By the lemma,
![]() $\omega $
is an involutive Hopf algebra anti-automorphism of
$\omega $
is an involutive Hopf algebra anti-automorphism of
![]() $Y_{\hbar }(\mathfrak {g})$
, which we call the Chevalley involution of
$Y_{\hbar }(\mathfrak {g})$
, which we call the Chevalley involution of
![]() $Y_{\hbar }(\mathfrak {g})$
. On
$Y_{\hbar }(\mathfrak {g})$
. On
![]() $\mathfrak {g}\subset Y_{\hbar }(\mathfrak {g})$
, this recovers the standard Chevalley involution, given by
$\mathfrak {g}\subset Y_{\hbar }(\mathfrak {g})$
, this recovers the standard Chevalley involution, given by
Similarly, under the identification
![]() $Y_{\hbar }(\mathfrak {g})/{\hbar } Y_{\hbar }(\mathfrak {g})\cong U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
, the semiclassical limit
$Y_{\hbar }(\mathfrak {g})/{\hbar } Y_{\hbar }(\mathfrak {g})\cong U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
, the semiclassical limit
![]() $\bar \omega : U({\mathfrak {t}}_{\scriptscriptstyle {+}})\to U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
of
$\bar \omega : U({\mathfrak {t}}_{\scriptscriptstyle {+}})\to U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
of
![]() $\omega $
coincides with the anti-involution of
$\omega $
coincides with the anti-involution of
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
uniquely extending the Lie algebra anti-automorphism
$U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
uniquely extending the Lie algebra anti-automorphism
In addition, we note that the composite
![]() $\unicode{x3ba} :=\omega \circ \varsigma $
is an involutive algebra automorphism of
$\unicode{x3ba} :=\omega \circ \varsigma $
is an involutive algebra automorphism of
![]() $Y_{\hbar }(\mathfrak {g})$
, given explicitly by
$Y_{\hbar }(\mathfrak {g})$
, given explicitly by
This automorphism is itself often called the Chevalley or Cartan involution of
![]() $Y_{\hbar }(\mathfrak {g})$
, though here we shall reserve the former terminology for
$Y_{\hbar }(\mathfrak {g})$
, though here we shall reserve the former terminology for
![]() $\omega $
.
$\omega $
.
3.4 Poincaré–Birkhoff–Witt theorem
An important foundational result in the theory of Yangians is the Poincaré–Birkhoff–Witt theorem, which asserts the flatness of
![]() $Y_{\hbar }(\mathfrak {g})$
as an
$Y_{\hbar }(\mathfrak {g})$
as an
![]() $\mathbb {N}$
-graded Hopf algebra deformation of
$\mathbb {N}$
-graded Hopf algebra deformation of
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
. It can be stated concisely as follows.
$U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
. It can be stated concisely as follows.
Theorem 3.4 The Yangian
![]() $Y_{\hbar }(\mathfrak {g})$
is a torsion-free
$Y_{\hbar }(\mathfrak {g})$
is a torsion-free
![]() $\mathbb {C}[{\hbar }]$
-module, and thus provides a flat deformation of
$\mathbb {C}[{\hbar }]$
-module, and thus provides a flat deformation of
![]() $Y_{\hbar }(\mathfrak {g})/{\hbar } Y_{\hbar }(\mathfrak {g})\cong U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
as a graded Hopf algebra over
$Y_{\hbar }(\mathfrak {g})/{\hbar } Y_{\hbar }(\mathfrak {g})\cong U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
as a graded Hopf algebra over
![]() $\mathbb {C}[{\hbar }]$
. In particular,
$\mathbb {C}[{\hbar }]$
. In particular,
![]() $Y_{\hbar }(\mathfrak {g})$
is isomorphic to
$Y_{\hbar }(\mathfrak {g})$
is isomorphic to
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {+}})[{\hbar }]$
as an
$U({\mathfrak {t}}_{\scriptscriptstyle {+}})[{\hbar }]$
as an
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-module.
$\mathbb {C}[{\hbar }]$
-module.
As
![]() $Y_{\hbar }(\mathfrak {g})$
is an
$Y_{\hbar }(\mathfrak {g})$
is an
![]() $\mathbb {N}$
-graded algebra deformation of
$\mathbb {N}$
-graded algebra deformation of
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
, an isomorphism
$U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
, an isomorphism
![]() $Y_{\hbar }(\mathfrak {g})\cong U({\mathfrak {t}}_{\scriptscriptstyle {+}})[{\hbar }]$
can be obtained by specifying an ordered, homogeneous, lift
$Y_{\hbar }(\mathfrak {g})\cong U({\mathfrak {t}}_{\scriptscriptstyle {+}})[{\hbar }]$
can be obtained by specifying an ordered, homogeneous, lift
![]() $ {G}\subset Y_{\hbar }(\mathfrak {g})$
of any fixed homogeneous basis of the Lie algebra
$ {G}\subset Y_{\hbar }(\mathfrak {g})$
of any fixed homogeneous basis of the Lie algebra
![]() ${\mathfrak {t}}_{\scriptscriptstyle {+}}$
. For our purposes, it will be useful to specify a class of isomorphisms of this type with a number of useful properties.
${\mathfrak {t}}_{\scriptscriptstyle {+}}$
. For our purposes, it will be useful to specify a class of isomorphisms of this type with a number of useful properties.
For each
![]() $\beta \in \Delta ^+$
, we may choose
$\beta \in \Delta ^+$
, we may choose
![]() $i(\beta )\in \mathbf {I}$
and
$i(\beta )\in \mathbf {I}$
and
![]() $\mathbf {X}^\beta \in U(\mathfrak {n}_{+})_{\beta -\alpha _{i(\beta )}}\subset U(\mathfrak {g})$
such that
$\mathbf {X}^\beta \in U(\mathfrak {n}_{+})_{\beta -\alpha _{i(\beta )}}\subset U(\mathfrak {g})$
such that
satisfy the duality condition
![]() $(x_\beta ^+,x_\beta ^-)=1$
, where
$(x_\beta ^+,x_\beta ^-)=1$
, where
![]() $\mathbf {X}^\beta $
acts on
$\mathbf {X}^\beta $
acts on
![]() $x_{i(\beta )}^+$
via the adjoint action of
$x_{i(\beta )}^+$
via the adjoint action of
![]() $\mathfrak {g}$
on
$\mathfrak {g}$
on
![]() $U(\mathfrak {g})$
. In particular, we can (and shall) take
$U(\mathfrak {g})$
. In particular, we can (and shall) take
![]() $\mathbf {X}^{\alpha _i}=1$
for all
$\mathbf {X}^{\alpha _i}=1$
for all
![]() $i\in \mathbf {I}$
, so that
$i\in \mathbf {I}$
, so that
![]() $x_{\alpha _i}^\pm =x_i^\pm $
. For each
$x_{\alpha _i}^\pm =x_i^\pm $
. For each
![]() $k\in \mathbb {N}$
, we then set
$k\in \mathbb {N}$
, we then set
where
![]() $\mathfrak {g}$
now operates on
$\mathfrak {g}$
now operates on
![]() $Y_{\hbar }(\mathfrak {g})$
via the adjoint action. This definition is such that
$Y_{\hbar }(\mathfrak {g})$
via the adjoint action. This definition is such that
![]() $q(x_{\beta ,k}^\pm )=x_\beta ^\pm t^k$
for all
$q(x_{\beta ,k}^\pm )=x_\beta ^\pm t^k$
for all
![]() $\beta \in \Delta ^+$
and
$\beta \in \Delta ^+$
and
![]() $k\in \mathbb {N}$
, and hence the set of elements
$k\in \mathbb {N}$
, and hence the set of elements
reduces modulo
![]() ${\hbar }$
to the basis of
${\hbar }$
to the basis of
![]() ${\mathfrak {t}}_{\scriptscriptstyle {+}}$
consisting of all Cartan elements
${\mathfrak {t}}_{\scriptscriptstyle {+}}$
consisting of all Cartan elements
![]() $h_i t^k$
and root vector
$h_i t^k$
and root vector
![]() $x_\beta ^\pm t^k$
. For each choice of total order
$x_\beta ^\pm t^k$
. For each choice of total order
![]() $\preceq $
on
$\preceq $
on
![]() $ {G}$
, the corresponding set of ordered monomials
$ {G}$
, the corresponding set of ordered monomials
is therefore a homogeneous basis of the
![]() $\mathbb {C}[{\hbar }]$
-module
$\mathbb {C}[{\hbar }]$
-module
![]() $Y_{\hbar }(\mathfrak {g})$
, and so defines an isomorphism
$Y_{\hbar }(\mathfrak {g})$
, and so defines an isomorphism
![]() $\mathbb {N}$
-graded modules
$\mathbb {N}$
-graded modules
uniquely determined by the property that
![]() $\unicode{x3bd} _{ {G}}|_{B( {G})}$
coincides with the restriction of the quotient map q to
$\unicode{x3bd} _{ {G}}|_{B( {G})}$
coincides with the restriction of the quotient map q to
![]() $B( {G})$
. We note that
$B( {G})$
. We note that
![]() $\unicode{x3bd} _{ {G}}$
is automatically an isomorphism of
$\unicode{x3bd} _{ {G}}$
is automatically an isomorphism of
![]() $\mathfrak {h}$
-modules, and is thus Q-graded.
$\mathfrak {h}$
-modules, and is thus Q-graded.
We shall single out a subclass of isomorphisms of this type which are compatible with Chevalley involutions and satisfy a triangularity condition. To make this precise, we must first recall that
![]() $Y_{\hbar }(\mathfrak {g})$
admits a triangular decomposition, compatible with the decomposition
$Y_{\hbar }(\mathfrak {g})$
admits a triangular decomposition, compatible with the decomposition
Let us define
![]() $Y_{\hbar }^0(\mathfrak {g})$
and
$Y_{\hbar }^0(\mathfrak {g})$
and
![]() $Y_{\hbar }^\pm (\mathfrak {g})$
to be the unital associative subalgebras of
$Y_{\hbar }^\pm (\mathfrak {g})$
to be the unital associative subalgebras of
![]() $Y_{\hbar }(\mathfrak {g})$
generated by
$Y_{\hbar }(\mathfrak {g})$
generated by
![]() $\{h_{ir}\}_{i\in \mathbf {I},r\in \mathbb {N}}$
and
$\{h_{ir}\}_{i\in \mathbf {I},r\in \mathbb {N}}$
and
![]() $\{x_{ir}^\pm \}_{i\in \mathbf {I},r\in \mathbb {N}}$
, respectively. These are
$\{x_{ir}^\pm \}_{i\in \mathbf {I},r\in \mathbb {N}}$
, respectively. These are
![]() $\mathbb {N}\times Q$
-graded subalgebras of
$\mathbb {N}\times Q$
-graded subalgebras of
![]() $Y_{\hbar }(\mathfrak {g})$
. The triangular decomposition of
$Y_{\hbar }(\mathfrak {g})$
. The triangular decomposition of
![]() $Y_{\hbar }(\mathfrak {g})$
is then encoded by the following proposition, which is a well-known consequence of Theorem 3.4.
$Y_{\hbar }(\mathfrak {g})$
is then encoded by the following proposition, which is a well-known consequence of Theorem 3.4.
Proposition 3.5
-
(1)
 $Y_{\hbar }^\pm (\mathfrak {g})$
is isomorphic to the unital, associative
$Y_{\hbar }^\pm (\mathfrak {g})$
is isomorphic to the unital, associative
 $\mathbb {C}[{\hbar }]$
-algebra generated by the set
$\mathbb {C}[{\hbar }]$
-algebra generated by the set
 $\{x_{ir}^\pm \}_{i\in \mathbf {I},r\in \mathbb {N}}$
, subject to relations (3.5) and (3.6) of Definition 6.1: where all indices are constrained as in Definition 6.1. In particular,
$\{x_{ir}^\pm \}_{i\in \mathbf {I},r\in \mathbb {N}}$
, subject to relations (3.5) and (3.6) of Definition 6.1: where all indices are constrained as in Definition 6.1. In particular, $$ \begin{gather*} [x_{i,r+1}^\pm,x_{js}^\pm]-[x_{ir}^\pm,x_{j,s+1}^\pm]=\pm {\hbar} d_{ij}(x_{ir}^\pm x_{js}^\pm+x_{js}^\pm x_{ir}^\pm ),\\ \sum_{\pi \in S_{m}} \left[x_{i,r_{\pi(1)}}^{\pm}, \left[x_{i,r_{\pi(2)}}^{\pm}, \cdots, \left[x_{i,r_{\pi(m)}}^{\pm},x_{js}^{\pm}\right] \cdots\right]\right] = 0, \end{gather*} $$
$$ \begin{gather*} [x_{i,r+1}^\pm,x_{js}^\pm]-[x_{ir}^\pm,x_{j,s+1}^\pm]=\pm {\hbar} d_{ij}(x_{ir}^\pm x_{js}^\pm+x_{js}^\pm x_{ir}^\pm ),\\ \sum_{\pi \in S_{m}} \left[x_{i,r_{\pi(1)}}^{\pm}, \left[x_{i,r_{\pi(2)}}^{\pm}, \cdots, \left[x_{i,r_{\pi(m)}}^{\pm},x_{js}^{\pm}\right] \cdots\right]\right] = 0, \end{gather*} $$
 $Y_{\hbar }^\pm (\mathfrak {g})$
is an
$Y_{\hbar }^\pm (\mathfrak {g})$
is an
 $\mathbb {N}$
-graded, torsion-free
$\mathbb {N}$
-graded, torsion-free
 $\mathbb {C}[{\hbar }]$
-algebra deformation of
$\mathbb {C}[{\hbar }]$
-algebra deformation of
 $U({\mathfrak {n}}_{\pm }[t])$
.
$U({\mathfrak {n}}_{\pm }[t])$
.
-
(2) The assignment
 $h_{ik}\mapsto h_it^k$
, for all
$h_{ik}\mapsto h_it^k$
, for all
 $i\in \mathbf {I}$
and
$i\in \mathbf {I}$
and
 $k\in \mathbb {N}$
, extends to an isomorphism of
$k\in \mathbb {N}$
, extends to an isomorphism of
 $\mathbb {N}$
-graded, commutative
$\mathbb {N}$
-graded, commutative
 $\mathbb {C}[{\hbar }]$
-algebras
$\mathbb {C}[{\hbar }]$
-algebras 
-
(3) The multiplication map
is an isomorphism of graded $$ \begin{align*} m:Y_{\hbar}^+(\mathfrak{g})\otimes Y_{\hbar}^0(\mathfrak{g})\otimes Y_{\hbar}^-(\mathfrak{g})\to Y_{\hbar}(\mathfrak{g}) \end{align*} $$
$$ \begin{align*} m:Y_{\hbar}^+(\mathfrak{g})\otimes Y_{\hbar}^0(\mathfrak{g})\otimes Y_{\hbar}^-(\mathfrak{g})\to Y_{\hbar}(\mathfrak{g}) \end{align*} $$
 $\mathbb {C}[{\hbar }]$
-modules.
$\mathbb {C}[{\hbar }]$
-modules.
As a consequence of Part (1) of Proposition 3.5 and Corollary 2.6, one has
![]() $Y_{\hbar }^\pm (\mathfrak {g})\cong U({\mathfrak {n}}_\pm [t])[{\hbar }]$
as
$Y_{\hbar }^\pm (\mathfrak {g})\cong U({\mathfrak {n}}_\pm [t])[{\hbar }]$
as
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-modules. Following the procedure outlined at the beginning of the section, let us fix an arbitrary total order
$\mathbb {C}[{\hbar }]$
-modules. Following the procedure outlined at the beginning of the section, let us fix an arbitrary total order
![]() $\preceq _{\scriptscriptstyle +}$
on the union
$\preceq _{\scriptscriptstyle +}$
on the union
The set of ordered monomials
![]() $B( {G}_+)$
in
$B( {G}_+)$
in
![]() $ {G}_+$
is a basis of
$ {G}_+$
is a basis of
![]() $Y_{\hbar }^+(\mathfrak {g})$
, and thus gives rise to an isomorphism of
$Y_{\hbar }^+(\mathfrak {g})$
, and thus gives rise to an isomorphism of
![]() $\mathbb {N}\times Q$
-graded
$\mathbb {N}\times Q$
-graded
![]() $\mathbb {C}[{\hbar }]$
-modules
$\mathbb {C}[{\hbar }]$
-modules
sending each ordered monomial in
![]() $ {G}_+$
to its image in
$ {G}_+$
to its image in
![]() $Y_{\hbar }^+(\mathfrak {g})/{\hbar } Y_{\hbar }^+(\mathfrak {g})\cong U({\mathfrak {n}}_+[t])$
. Using the Chevalley involution
$Y_{\hbar }^+(\mathfrak {g})/{\hbar } Y_{\hbar }^+(\mathfrak {g})\cong U({\mathfrak {n}}_+[t])$
. Using the Chevalley involution
![]() $\omega $
and its semiclassical limit
$\omega $
and its semiclassical limit
![]() $\bar \omega $
(see (3.9)), we then obtain an isomorphism
$\bar \omega $
(see (3.9)), we then obtain an isomorphism
Combining
![]() $\unicode{x3bd} _\pm $
with
$\unicode{x3bd} _\pm $
with
![]() $\unicode{x3be} $
from Part (2) of Proposition 3.5 outputs an isomorphism of
$\unicode{x3be} $
from Part (2) of Proposition 3.5 outputs an isomorphism of
![]() $\mathbb {N}\times Q$
-graded
$\mathbb {N}\times Q$
-graded
![]() $\mathbb {C}[{\hbar }]$
-modules
$\mathbb {C}[{\hbar }]$
-modules
where ![]() is the multiplication map, which we extend trivially by
is the multiplication map, which we extend trivially by
![]() $\mathbb {C}[{\hbar }]$
-linearity. By construction,
$\mathbb {C}[{\hbar }]$
-linearity. By construction,
![]() $\unicode{x3bd} $
is compatible with the underlying triangular decompositions on
$\unicode{x3bd} $
is compatible with the underlying triangular decompositions on
![]() $Y_{\hbar }(\mathfrak {g})$
and
$Y_{\hbar }(\mathfrak {g})$
and
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
and satisfies
$U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
and satisfies
The definition (3.13) is such that
![]() $\unicode{x3bd} =\unicode{x3bd} _{ {G}}$
for any total order
$\unicode{x3bd} =\unicode{x3bd} _{ {G}}$
for any total order
![]() $\preceq $
on
$\preceq $
on
![]() $ {G}$
which restricts to
$ {G}$
which restricts to
![]() $\preceq _{\scriptscriptstyle {+}}$
, satisfies
$\preceq _{\scriptscriptstyle {+}}$
, satisfies
![]() $x^+\preceq h \preceq x^-$
for all
$x^+\preceq h \preceq x^-$
for all
![]() $x^{\pm }\in {G} \cap Y_{\hbar }^\pm (\mathfrak {g})$
and
$x^{\pm }\in {G} \cap Y_{\hbar }^\pm (\mathfrak {g})$
and
![]() $h\in Y_{\hbar }^0(\mathfrak {g})$
, and for which
$h\in Y_{\hbar }^0(\mathfrak {g})$
, and for which
![]() $\omega $
is a decreasing function on
$\omega $
is a decreasing function on
![]() $ {G}$
. We will denote the inverse of
$ {G}$
. We will denote the inverse of
![]() $\unicode{x3bd} $
by
$\unicode{x3bd} $
by
![]() $\mu $
:
$\mu $
:
Note that, for any total order on
![]() $ {G}$
, one has
$ {G}$
, one has
![]() $\mu (x)=\unicode{x3bd} _{ {G}}^{-1}(x)$
for all
$\mu (x)=\unicode{x3bd} _{ {G}}^{-1}(x)$
for all
![]() $x\in {G}$
.
$x\in {G}$
.
3.5 Quantization
As a consequence of Proposition 3.2 and Theorem 3.4, the Yangian
![]() $Y_{\hbar }(\mathfrak {g})$
provides a homogeneous quantization of an
$Y_{\hbar }(\mathfrak {g})$
provides a homogeneous quantization of an
![]() $\mathbb {N}$
-graded Lie bialgebra structure on the Lie algebra
$\mathbb {N}$
-graded Lie bialgebra structure on the Lie algebra
![]() ${\mathfrak {t}}_{\scriptscriptstyle {+}}$
over
${\mathfrak {t}}_{\scriptscriptstyle {+}}$
over
![]() $\mathbb {C}[{\hbar }]$
, with cocommutator
$\mathbb {C}[{\hbar }]$
, with cocommutator
![]() $\delta $
determined by the formula (2.2). By Proposition 3.2,
$\delta $
determined by the formula (2.2). By Proposition 3.2,
![]() $\delta $
is uniquely determined by
$\delta $
is uniquely determined by
![]() $\delta (\mathfrak {g})=0$
and
$\delta (\mathfrak {g})=0$
and
and thus coincides with
![]() $\delta _{\scriptscriptstyle +}$
from Section 2.5. This recovers the following well-known result, originally due to Drinfeld [Reference Drinfel’d6, Theorem 2]:
$\delta _{\scriptscriptstyle +}$
from Section 2.5. This recovers the following well-known result, originally due to Drinfeld [Reference Drinfel’d6, Theorem 2]:
Theorem 3.6
![]() $Y_{\hbar }(\mathfrak {g})$
is a homogeneous quantization of
$Y_{\hbar }(\mathfrak {g})$
is a homogeneous quantization of
![]() $({\mathfrak {t}}_{\scriptscriptstyle {+}},\delta _{\scriptscriptstyle +})$
over
$({\mathfrak {t}}_{\scriptscriptstyle {+}},\delta _{\scriptscriptstyle +})$
over
![]() $\mathbb {C}[{\hbar }]$
.
$\mathbb {C}[{\hbar }]$
.
As explained in Section 2.4, it follows immediately that the
![]() ${\hbar }$
-adic completion
${\hbar }$
-adic completion
is a homogeneous quantization of
![]() $({\mathfrak {t}}_{\scriptscriptstyle {+}},\delta _{\scriptscriptstyle +})$
over
$({\mathfrak {t}}_{\scriptscriptstyle {+}},\delta _{\scriptscriptstyle +})$
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. We refer the reader to Definition 2.12 and Corollary 2.6 for a detailed discussion of this point.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. We refer the reader to Definition 2.12 and Corollary 2.6 for a detailed discussion of this point.
Remark 3.7 Let
![]() $Y_{\hbar }^{\pm \!}\mathfrak {g}$
and
$Y_{\hbar }^{\pm \!}\mathfrak {g}$
and
![]() $Y_{\hbar }^0\mathfrak {g}$
denote the topological
$Y_{\hbar }^0\mathfrak {g}$
denote the topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras
It follows from Corollary 2.6 and Proposition 3.5 that these are subalgebras of
![]() $Y_{\hbar }\mathfrak {g}$
, with
$Y_{\hbar }\mathfrak {g}$
, with
![]() $Y_{\hbar }^0\mathfrak {g}$
isomorphic to
$Y_{\hbar }^0\mathfrak {g}$
isomorphic to
![]() $U(\mathfrak {h}[t])[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]\cong \mathsf {S}(\mathfrak {h}[t])[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as an
$U(\mathfrak {h}[t])[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]\cong \mathsf {S}(\mathfrak {h}[t])[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as an
![]() $\mathbb {N}$
-graded topological
$\mathbb {N}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra, and
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra, and
![]() $Y_{\hbar }^{\pm \!}\mathfrak {g}$
a topologically free
$Y_{\hbar }^{\pm \!}\mathfrak {g}$
a topologically free
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra with semiclassical limit equal to
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra with semiclassical limit equal to
![]() $U({\mathfrak {n}}_{\pm }[t])$
. By Part (3) of Proposition 3.5, the product m on
$U({\mathfrak {n}}_{\pm }[t])$
. By Part (3) of Proposition 3.5, the product m on
![]() $Y_{\hbar }\mathfrak {g}$
gives rise to an isomorphism of
$Y_{\hbar }\mathfrak {g}$
gives rise to an isomorphism of
![]() $\mathbb {N}$
-graded topological
$\mathbb {N}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
where, following Remark 2.11,
![]() $\otimes $
should now be understood to be the topological tensor product
$\otimes $
should now be understood to be the topological tensor product
![]() $\widehat {\otimes }$
of
$\widehat {\otimes }$
of
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules. For later purposes, we note that the product on
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules. For later purposes, we note that the product on
![]() $Y_{\hbar }\mathfrak {g}$
also gives rise to an isomorphism
$Y_{\hbar }\mathfrak {g}$
also gives rise to an isomorphism
which can be realized as
![]() $\unicode{x3ba} \circ m\circ (\unicode{x3ba} _-\otimes \unicode{x3ba} _0\otimes \unicode{x3ba} _+)$
, where m is the isomorphism (3.15),
$\unicode{x3ba} \circ m\circ (\unicode{x3ba} _-\otimes \unicode{x3ba} _0\otimes \unicode{x3ba} _+)$
, where m is the isomorphism (3.15),
![]() $\unicode{x3ba} $
is the involutive automorphism of
$\unicode{x3ba} $
is the involutive automorphism of
![]() $Y_{\hbar }\mathfrak {g}$
defined in (3.10) (extended by continuity), and
$Y_{\hbar }\mathfrak {g}$
defined in (3.10) (extended by continuity), and ![]() .
.
3.6 The universal R-matrix
We complete our survey of
![]() $Y_{\hbar }(\mathfrak {g})$
by reviewing the construction of the universal R-matrix
$Y_{\hbar }(\mathfrak {g})$
by reviewing the construction of the universal R-matrix
![]() $\mathcal {R}(z)$
of the Yangian, whose existence and uniqueness was first established by Drinfeld in [Reference Drinfel’d6, Theorem 3]. We shall, however, need a refined version of Drinfeld’s theorem only recently proven in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Section 7.4], which reconstructs
$\mathcal {R}(z)$
of the Yangian, whose existence and uniqueness was first established by Drinfeld in [Reference Drinfel’d6, Theorem 3]. We shall, however, need a refined version of Drinfeld’s theorem only recently proven in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Section 7.4], which reconstructs
![]() $\mathcal {R}(z)$
from the factors in its Gauss decomposition
$\mathcal {R}(z)$
from the factors in its Gauss decomposition
Let us begin with a few preliminaries. For each positive integer n, let
denote the algebra of formal Laurent series in
![]() $z^{-1}$
with coefficients in
$z^{-1}$
with coefficients in
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes n}$
. Following [Reference Wendlandt41, Section 4.2], we then introduce the subspace
$Y_{\hbar }(\mathfrak {g})^{\otimes n}$
. Following [Reference Wendlandt41, Section 4.2], we then introduce the subspace
where
![]() $(Y_{\hbar }(\mathfrak {g})^{\otimes n})_k$
is the kth graded component of the
$(Y_{\hbar }(\mathfrak {g})^{\otimes n})_k$
is the kth graded component of the
![]() $\mathbb {N}$
-graded algebra
$\mathbb {N}$
-graded algebra
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes n}$
. This is a
$Y_{\hbar }(\mathfrak {g})^{\otimes n}$
. This is a
![]() $\mathbb {C}$
-algebra isomorphic to the completion of
$\mathbb {C}$
-algebra isomorphic to the completion of
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes n}$
with respect to its grading. The
$Y_{\hbar }(\mathfrak {g})^{\otimes n}$
with respect to its grading. The
![]() $\mathbb {C}[z,z^{-1}]$
-submodule of
$\mathbb {C}[z,z^{-1}]$
-submodule of
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes n}[z;z^{-1}]\!\kern-1.2pt]$
that it generates is a
$Y_{\hbar }(\mathfrak {g})^{\otimes n}[z;z^{-1}]\!\kern-1.2pt]$
that it generates is a
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-algebra
$\mathbb {C}[{\hbar }]$
-algebra
Though for the moment we shall only be interested in the case where
![]() $n=2$
, such formal series spaces will reappear in later sections. In addition to the above, we shall make use of two functions
$n=2$
, such formal series spaces will reappear in later sections. In addition to the above, we shall make use of two functions
![]() $Q_+\to \mathbb {N}$
. First, we have the standard additive height function
$Q_+\to \mathbb {N}$
. First, we have the standard additive height function
![]() $\mathrm {ht}$
given by
$\mathrm {ht}$
given by
Second, we have an auxiliary function
![]() $\nu :Q_+\to \mathbb {N}$
defined by
$\nu :Q_+\to \mathbb {N}$
defined by
where it is understood that
![]() $\nu (0)=0$
.
$\nu (0)=0$
.
Let us now recall the construction of the factor
![]() $\mathcal {R}^-(z)$
. Fix a Cartan element
$\mathcal {R}^-(z)$
. Fix a Cartan element
where the union runs over all nonzero
![]() $\beta \in Q_+$
. We then introduce
$\beta \in Q_+$
. We then introduce
by setting
![]() $\mathcal {R}^-_0(z)=1$
and defining
$\mathcal {R}^-_0(z)=1$
and defining
![]() $\mathcal {R}^-_\beta (z)$
inductively in
$\mathcal {R}^-_\beta (z)$
inductively in
![]() $\mathrm {ht}(\beta )$
using the formula
$\mathrm {ht}(\beta )$
using the formula
 $$ \begin{align} \mathcal{R}^-_\beta(z)= {\hbar}\sum_{p\geq 0} \frac{\mathbf{T}(\zeta)^p}{(z\beta(\zeta))^{p+1}} \sum_{\alpha\in \Delta^+}\alpha(\zeta)\mathcal{R}_{\beta-\alpha}(z) (x_{\alpha}^- \otimes x_{\alpha}^+ ), \end{align} $$
$$ \begin{align} \mathcal{R}^-_\beta(z)= {\hbar}\sum_{p\geq 0} \frac{\mathbf{T}(\zeta)^p}{(z\beta(\zeta))^{p+1}} \sum_{\alpha\in \Delta^+}\alpha(\zeta)\mathcal{R}_{\beta-\alpha}(z) (x_{\alpha}^- \otimes x_{\alpha}^+ ), \end{align} $$
where
![]() $\mathcal {R}_{\gamma }(z)=0$
whenever
$\mathcal {R}_{\gamma }(z)=0$
whenever
![]() $\gamma \notin Q_+$
and
$\gamma \notin Q_+$
and
![]() $ \mathbf {T}(\zeta )=\mathrm {ad}(\mathrm {T}(\zeta )\otimes 1 + 1\otimes \mathrm {T}(\zeta )), $
with
$ \mathbf {T}(\zeta )=\mathrm {ad}(\mathrm {T}(\zeta )\otimes 1 + 1\otimes \mathrm {T}(\zeta )), $
with
![]() $\mathrm {T}:\mathfrak {h}\to Y_{\hbar }^0(\mathfrak {g})$
the embedding determined by
$\mathrm {T}:\mathfrak {h}\to Y_{\hbar }^0(\mathfrak {g})$
the embedding determined by
Using the fact that, for each
![]() $p\in \mathbb {N}$
,
$p\in \mathbb {N}$
,
![]() $\mathbf {T}(\zeta )^p z^{-p-1}$
is a homogeneous operator on
$\mathbf {T}(\zeta )^p z^{-p-1}$
is a homogeneous operator on
![]() $ {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)$
of degree
$ {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)$
of degree
![]() $-1$
, one deduces from the recursive formula (3.18) that
$-1$
, one deduces from the recursive formula (3.18) that
As the set
![]() $\{\beta \in Q_+: \nu (\beta )\leq k\}$
is finite for any
$\{\beta \in Q_+: \nu (\beta )\leq k\}$
is finite for any
![]() $k\in \mathbb {N}$
, we obtain a well-defined formal series
$k\in \mathbb {N}$
, we obtain a well-defined formal series
which by construction satisfies
![]() $ \mathcal {R}^-(z)\in 1+{\hbar } {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)_{-1}\subset \widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z. $
$ \mathcal {R}^-(z)\in 1+{\hbar } {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)_{-1}\subset \widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z. $
By Theorem 4.1 of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17],
![]() $\mathcal {R}^-(z)$
is independent of the choice of
$\mathcal {R}^-(z)$
is independent of the choice of
![]() $\zeta \in \mathfrak {h}$
made above and satisfies a number of remarkable properties. Notably, it intertwines
$\zeta \in \mathfrak {h}$
made above and satisfies a number of remarkable properties. Notably, it intertwines
![]() $\tau _z\otimes \mathbf {1} \circ \Delta $
and the formal, deformed Drinfeld coproduct
$\tau _z\otimes \mathbf {1} \circ \Delta $
and the formal, deformed Drinfeld coproduct ![]() on
on
![]() $Y_{\hbar }(\mathfrak {g})$
, as defined in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Section 3.4]. We will not make direct use of these properties here, and refer the reader to [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17] for a detailed treatment of
$Y_{\hbar }(\mathfrak {g})$
, as defined in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Section 3.4]. We will not make direct use of these properties here, and refer the reader to [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17] for a detailed treatment of
![]() $\mathcal {R}^-(z)$
.
$\mathcal {R}^-(z)$
.
Let us now recall the definition of the abelian R-matrix
![]() $\mathcal {R}^0(z)\in Y_{\hbar }^0(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
from [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Section 6]. Let
$\mathcal {R}^0(z)\in Y_{\hbar }^0(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
from [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Section 6]. Let
![]() $\mathbf {B}=(d_i a_{ij})$
denote the symmetrization of the Cartan matrix
$\mathbf {B}=(d_i a_{ij})$
denote the symmetrization of the Cartan matrix
![]() $\mathbf {A}$
. Given an indeterminate v, we let
$\mathbf {A}$
. Given an indeterminate v, we let
![]() $\mathbf {B}(v)=([d_i a_{ij}]_v)\subset {\mathrm {GL}}_{\mathbf {I}}(\mathbb {Q}(v))$
be the associated matrix of v-numbers, where
$\mathbf {B}(v)=([d_i a_{ij}]_v)\subset {\mathrm {GL}}_{\mathbf {I}}(\mathbb {Q}(v))$
be the associated matrix of v-numbers, where
Then it is known [Reference Gautam and Toledano Laredo16, Theorem A.1] that the auxiliary matrix
has entries
![]() $c_{ij}(v)$
in
$c_{ij}(v)$
in
![]() $\mathbb {N}[v,v^{-1}]$
, where
$\mathbb {N}[v,v^{-1}]$
, where
![]() $4\kappa $
is the eigenvalue of the Casimir element of
$4\kappa $
is the eigenvalue of the Casimir element of
![]() $\mathfrak {g}$
in the adjoint representation.
$\mathfrak {g}$
in the adjoint representation.
Next, for each index
![]() $i\in \mathbf {I}$
, we introduce the series
$i\in \mathbf {I}$
, we introduce the series
![]() $t_i(u)\in {\hbar } Y_{\hbar }^0(\mathfrak {g})[\kern-1.2pt\![u^{-1}]\!\kern-1.2pt]$
and its inverse Borel transform
$t_i(u)\in {\hbar } Y_{\hbar }^0(\mathfrak {g})[\kern-1.2pt\![u^{-1}]\!\kern-1.2pt]$
and its inverse Borel transform
![]() $B_i(u)\in {\hbar } Y_{\hbar }^0(\mathfrak {g})[\kern-1.2pt\![u]\!\kern-1.2pt]$
by
$B_i(u)\in {\hbar } Y_{\hbar }^0(\mathfrak {g})[\kern-1.2pt\![u]\!\kern-1.2pt]$
by
Note that
![]() $t_{i1}$
coincides with the element of the same name introduced in Section 3.2. From these data, we obtain an element
$t_{i1}$
coincides with the element of the same name introduced in Section 3.2. From these data, we obtain an element
![]() $\mathcal {L}(z)\in ({\hbar }/z)^2 Y_{\hbar }^0(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
defined by
$\mathcal {L}(z)\in ({\hbar }/z)^2 Y_{\hbar }^0(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
defined by
where T is the shift operator
![]() $T(f(z))=f(z+\frac {{\hbar }}{2})$
on
$T(f(z))=f(z+\frac {{\hbar }}{2})$
on
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. Equivalently,
$Y_{\hbar }(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. Equivalently,
As
![]() $\mathcal {L}(z)\in {\hbar } z^{-2}Y_{\hbar }^0(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
and
$\mathcal {L}(z)\in {\hbar } z^{-2}Y_{\hbar }^0(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
and
![]() $Y_{\hbar }^0(\mathfrak {g})^{\otimes 2}$
is torsion-free, there is a unique solution
$Y_{\hbar }^0(\mathfrak {g})^{\otimes 2}$
is torsion-free, there is a unique solution
![]() $\mathcal {S}(z)$
to the formal difference equation
$\mathcal {S}(z)$
to the formal difference equation
If
![]() $g(z)\in z^{-1}\mathbb {C}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
is the unique solution of
$g(z)\in z^{-1}\mathbb {C}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
is the unique solution of
![]() $-z^{-2}=g(z+1)-g(z)$
, then by Proposition 6.6 of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17], we have
$-z^{-2}=g(z+1)-g(z)$
, then by Proposition 6.6 of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17], we have
 $$ \begin{align} \mathcal{S}(z)=\frac{T^{2\kappa}}{(2\kappa{\hbar})^2}\sum_{i,j\in \mathbf{I}}c_{ij}(T)B_i(\partial_z)\otimes B_j(-\partial_z) \left(g\!\left(\frac{z}{2\kappa{\hbar}}\right)\right), \end{align} $$
$$ \begin{align} \mathcal{S}(z)=\frac{T^{2\kappa}}{(2\kappa{\hbar})^2}\sum_{i,j\in \mathbf{I}}c_{ij}(T)B_i(\partial_z)\otimes B_j(-\partial_z) \left(g\!\left(\frac{z}{2\kappa{\hbar}}\right)\right), \end{align} $$
where
![]() $g(z/2\kappa {\hbar })$
is viewed as an element of
$g(z/2\kappa {\hbar })$
is viewed as an element of
![]() $ {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)$
. The abelian R-matrix
$ {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)$
. The abelian R-matrix
![]() $\mathcal {R}^0(z)$
is defined to be the formal series exponential of this solution:
$\mathcal {R}^0(z)$
is defined to be the formal series exponential of this solution:
Equivalently, it is the unique formal solution in
![]() $1+z^{-1}Y_{\hbar }^0(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
of the equation
$1+z^{-1}Y_{\hbar }^0(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
of the equation
where
![]() $\mathcal {A}(z)=\exp (\mathcal {L}(z))$
. As T and
$\mathcal {A}(z)=\exp (\mathcal {L}(z))$
. As T and
![]() ${\hbar }^{-2}B_i(\partial _z)\otimes B_j(-\partial _z)$
are homogeneous operators of degree zero on
${\hbar }^{-2}B_i(\partial _z)\otimes B_j(-\partial _z)$
are homogeneous operators of degree zero on
![]() $ {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)$
, it follows from (3.19) that
$ {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)$
, it follows from (3.19) that
We are now in a position to introduce the universal R-matrix of the Yangian. Set
![]() $\mathcal {R}^+(z)=\mathcal {R}_{21}^-(-z)^{-1}$
and define
$\mathcal {R}^+(z)=\mathcal {R}_{21}^-(-z)^{-1}$
and define
The following result is the content of Theorem 7.4 of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17].
Theorem 3.8
![]() $\mathcal {R}(z)$
is the unique formal series in
$\mathcal {R}(z)$
is the unique formal series in
![]() $ 1+z^{-1}Y_{\hbar }(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt] $
satisfying the intertwiner equation
$ 1+z^{-1}Y_{\hbar }(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt] $
satisfying the intertwiner equation
in
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes 2}[z;z^{-1}]\!\kern-1.2pt]$
, in addition to the cabling identities
$Y_{\hbar }(\mathfrak {g})^{\otimes 2}[z;z^{-1}]\!\kern-1.2pt]$
, in addition to the cabling identities
 $$ \begin{align*} \Delta\otimes \mathbf{1} (\mathcal{R}(z))&= \mathcal{R}_{13}(z)\mathcal{R}_{23}(z),\\ \mathbf{1}\otimes \Delta (\mathcal{R}(z))&= \mathcal{R}_{13}(z)\mathcal{R}_{12}(z) \end{align*} $$
$$ \begin{align*} \Delta\otimes \mathbf{1} (\mathcal{R}(z))&= \mathcal{R}_{13}(z)\mathcal{R}_{23}(z),\\ \mathbf{1}\otimes \Delta (\mathcal{R}(z))&= \mathcal{R}_{13}(z)\mathcal{R}_{12}(z) \end{align*} $$
in
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes 3}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. Moreover,
$Y_{\hbar }(\mathfrak {g})^{\otimes 3}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. Moreover,
![]() $\mathcal {R}(z)$
has the following properties:
$\mathcal {R}(z)$
has the following properties:
-
(1) It is unitary:
 $\mathcal {R}(z)^{-1}=\mathcal {R}_{21}(-z)$
.
$\mathcal {R}(z)^{-1}=\mathcal {R}_{21}(-z)$
. -
(2) For any
 $a,b\in \mathbb {C}$
, one has
$a,b\in \mathbb {C}$
, one has  $$ \begin{align*} (\tau_a\otimes \tau_b)\mathcal{R}(z)=\mathcal{R}(z+a-b). \end{align*} $$
$$ \begin{align*} (\tau_a\otimes \tau_b)\mathcal{R}(z)=\mathcal{R}(z+a-b). \end{align*} $$
-
(3)
 $\mathcal {R}(z)$
is a homogeneous, degree zero, element of
$\mathcal {R}(z)$
is a homogeneous, degree zero, element of
 $ {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)$
, with and semiclassical limit given by
$ {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)$
, with and semiclassical limit given by $$ \begin{align*} \mathcal{R}(z)-1\in {\hbar} {L}(\widehat{Y_{\hbar}\mathfrak{g}}{\vphantom{Y_{\hbar}\mathfrak{g}}}^{\scriptscriptstyle{(2)}}_z)_{-1}= {\hbar} z^{-1}\widehat{Y_{\hbar}\mathfrak{g}}{\vphantom{Y_{\hbar}\mathfrak{g}}}^{\scriptscriptstyle{(2)}}_z \end{align*} $$
$$ \begin{align*} \mathcal{R}(z)-1\in {\hbar} {L}(\widehat{Y_{\hbar}\mathfrak{g}}{\vphantom{Y_{\hbar}\mathfrak{g}}}^{\scriptscriptstyle{(2)}}_z)_{-1}= {\hbar} z^{-1}\widehat{Y_{\hbar}\mathfrak{g}}{\vphantom{Y_{\hbar}\mathfrak{g}}}^{\scriptscriptstyle{(2)}}_z \end{align*} $$
 $$ \begin{align*} q^{\otimes 2} {\hbar}^{-1}({\mathcal{R}(z)-1})=\frac{\Omega_{\mathfrak{g}}}{z+t-w}\in (U(\mathfrak{g}[t])\otimes U(\mathfrak{g}[w]))[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]. \end{align*} $$
$$ \begin{align*} q^{\otimes 2} {\hbar}^{-1}({\mathcal{R}(z)-1})=\frac{\Omega_{\mathfrak{g}}}{z+t-w}\in (U(\mathfrak{g}[t])\otimes U(\mathfrak{g}[w]))[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]. \end{align*} $$
The series
![]() $\mathcal {R}(z)$
is called the universal R-matrix of the Yangian, and is related to the element
$\mathcal {R}(z)$
is called the universal R-matrix of the Yangian, and is related to the element
![]() $\mathcal {R}^D(z)\in Y_{\hbar }(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
introduced by Drinfeld in Theorem 3 of [Reference Drinfel’d6] by
$\mathcal {R}^D(z)\in Y_{\hbar }(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
introduced by Drinfeld in Theorem 3 of [Reference Drinfel’d6] by
![]() $\mathcal {R}(z)=\mathcal {R}^D(-z)^{-1}$
(see Section 1.1 and Corollary 7.4 of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17]).
$\mathcal {R}(z)=\mathcal {R}^D(-z)^{-1}$
(see Section 1.1 and Corollary 7.4 of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17]).
Remark 3.9 Strictly speaking, the results of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17] are stated with
![]() ${\hbar }$
replaced by an arbitrary nonzero complex number. However, it is easy to translate between the numerical and formal
${\hbar }$
replaced by an arbitrary nonzero complex number. However, it is easy to translate between the numerical and formal
![]() ${\hbar }$
settings via a homogenization procedure, and for the sake of completeness we make this rigorous in Appendix Appendix A (see Proposition A.1).
${\hbar }$
settings via a homogenization procedure, and for the sake of completeness we make this rigorous in Appendix Appendix A (see Proposition A.1).
The final result of this section shows that, in particular,
![]() $\mathcal {R}(z)$
is invariant under the Chevalley involution
$\mathcal {R}(z)$
is invariant under the Chevalley involution
![]() $\omega $
of Section 3.3.
$\omega $
of Section 3.3.
Corollary 3.10 The universal R-matrix
![]() $\mathcal {R}(z)$
satisfies
$\mathcal {R}(z)$
satisfies
Proof Set
![]() $\mathcal {R}^\omega (z):=(\omega \otimes \omega )\mathcal {R}(z)$
and
$\mathcal {R}^\omega (z):=(\omega \otimes \omega )\mathcal {R}(z)$
and
![]() $\mathcal {R}^\varsigma (z):=(\varsigma \otimes \varsigma )\mathcal {R}(z)$
. Applying the anti-automorphisms
$\mathcal {R}^\varsigma (z):=(\varsigma \otimes \varsigma )\mathcal {R}(z)$
. Applying the anti-automorphisms
![]() $\omega \otimes \omega $
and
$\omega \otimes \omega $
and
![]() $\varsigma \otimes \varsigma $
to the intertwiner equation (8.3), while making use of the relations of Lemma 3.3, we find that
$\varsigma \otimes \varsigma $
to the intertwiner equation (8.3), while making use of the relations of Lemma 3.3, we find that

for all
![]() $x\in Y_{\hbar }(\mathfrak {g})$
. Hence,
$x\in Y_{\hbar }(\mathfrak {g})$
. Hence,
![]() $\mathcal {R}^\omega (z)$
and
$\mathcal {R}^\omega (z)$
and
![]() $\mathcal {R}^\varsigma (-z)^{-1}=\mathcal {R}_{21}^{\varsigma }(z)$
are both solutions of (8.3). One verifies similarly that these both satisfy the cabling identities, and hence coincide with
$\mathcal {R}^\varsigma (-z)^{-1}=\mathcal {R}_{21}^{\varsigma }(z)$
are both solutions of (8.3). One verifies similarly that these both satisfy the cabling identities, and hence coincide with
![]() $\mathcal {R}(z)$
by the uniqueness statement of Theorem 3.8. Since
$\mathcal {R}(z)$
by the uniqueness statement of Theorem 3.8. Since
![]() $\unicode{x3ba} =\varsigma \circ \omega $
, this completes the proof of the proposition.
$\unicode{x3ba} =\varsigma \circ \omega $
, this completes the proof of the proposition.
4 The Yangian double
We now recall the definition and main properties of the Yangian double
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
, including a review of some of the results of [Reference Wendlandt41]. These results, summarized in Theorems 4.6 and 4.8, will play an integral role in establishing in Sections 7 and 8 that
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
, including a review of some of the results of [Reference Wendlandt41]. These results, summarized in Theorems 4.6 and 4.8, will play an integral role in establishing in Sections 7 and 8 that
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a homogeneous quantization of the Lie bialgebra
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a homogeneous quantization of the Lie bialgebra
![]() $\mathfrak {t}=\mathfrak {g}[t^{\pm 1}]$
isomorphic to the restricted quantum double of the Yangian.
$\mathfrak {t}=\mathfrak {g}[t^{\pm 1}]$
isomorphic to the restricted quantum double of the Yangian.
4.1 The Yangian double
The definition of the Yangian double
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is obtained by allowing the second index of the generators in Definition 6.1 to take values in
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is obtained by allowing the second index of the generators in Definition 6.1 to take values in
![]() $\mathbb {Z}$
, while working in the category of topological
$\mathbb {Z}$
, while working in the category of topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras:
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras:
Definition 4.1 The Yangian double
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is the unital, associative
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is the unital, associative
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra topologically generated by
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra topologically generated by
![]() $\{x_{ir}^\pm , h_{ir}\}_{i\in \mathbf {I},r\in \mathbb {Z}}$
, subject to the relations (3.1)–(3.6) of Definition 6.1. In terms of generating series
$\{x_{ir}^\pm , h_{ir}\}_{i\in \mathbf {I},r\in \mathbb {Z}}$
, subject to the relations (3.1)–(3.6) of Definition 6.1. In terms of generating series
these defining relations can be expressed as follows, for
![]() $i,j\in \mathbf {I}$
:
$i,j\in \mathbf {I}$
:
 $$ \begin{gather*} [\mathcal{H}_{i}(u),\mathcal{H}_j(v)] =0,\\ [h_{i0},\mathcal{X}_j^\pm(u)]=\pm 2d_{ij}\mathcal{X}_j^\pm(u), \\ \left(u-v\mp{\hbar} d_{ij}\right)\mathcal{H}_i(u)\mathcal{X}_j^{\pm}(v)=\left(u-v\pm{\hbar} d_{ij}\right)\mathcal{X}_j^{\pm}(v)\mathcal{H}_i(u), \\ \left(u-v\mp{\hbar} d_{ij}\right)\mathcal{X}_{i}^{\pm}(u)\mathcal{X}_{j}^{\pm}(v) =\left(u-v\pm{\hbar} d_{ij}\right) \mathcal{X}_{j}^{\pm}(v)\mathcal{X}_{i}^{\pm}(u) , \\ [\mathcal{X}_i^+(u),\mathcal{X}_j^-(v)] =\delta_{ij} u^{-1}\delta(v/u)\mathcal{H}_i(v), \\ \sum_{\pi \in S_{m}} \left[\mathcal{X}_i^{\pm}(u_{\pi(1)}), \left[\mathcal{X}_i^{\pm}(u_{\pi(2)}), \ldots, \left[\mathcal{X}_i^{\pm}(u_{\pi(m)}),\mathcal{X}_j^{\pm}(v)\right] \cdots\right]\right] = 0, \end{gather*} $$
$$ \begin{gather*} [\mathcal{H}_{i}(u),\mathcal{H}_j(v)] =0,\\ [h_{i0},\mathcal{X}_j^\pm(u)]=\pm 2d_{ij}\mathcal{X}_j^\pm(u), \\ \left(u-v\mp{\hbar} d_{ij}\right)\mathcal{H}_i(u)\mathcal{X}_j^{\pm}(v)=\left(u-v\pm{\hbar} d_{ij}\right)\mathcal{X}_j^{\pm}(v)\mathcal{H}_i(u), \\ \left(u-v\mp{\hbar} d_{ij}\right)\mathcal{X}_{i}^{\pm}(u)\mathcal{X}_{j}^{\pm}(v) =\left(u-v\pm{\hbar} d_{ij}\right) \mathcal{X}_{j}^{\pm}(v)\mathcal{X}_{i}^{\pm}(u) , \\ [\mathcal{X}_i^+(u),\mathcal{X}_j^-(v)] =\delta_{ij} u^{-1}\delta(v/u)\mathcal{H}_i(v), \\ \sum_{\pi \in S_{m}} \left[\mathcal{X}_i^{\pm}(u_{\pi(1)}), \left[\mathcal{X}_i^{\pm}(u_{\pi(2)}), \ldots, \left[\mathcal{X}_i^{\pm}(u_{\pi(m)}),\mathcal{X}_j^{\pm}(v)\right] \cdots\right]\right] = 0, \end{gather*} $$
where
![]() $\delta (u)=\sum _{r\in \mathbb {Z}}u^r\in \mathbb {C}[\kern-1.2pt\![u^{\pm 1}]\!\kern-1.2pt]$
is the formal delta function and in the last relation
$\delta (u)=\sum _{r\in \mathbb {Z}}u^r\in \mathbb {C}[\kern-1.2pt\![u^{\pm 1}]\!\kern-1.2pt]$
is the formal delta function and in the last relation
![]() $i\neq j$
and
$i\neq j$
and
![]() $m=1-a_{ij}$
.
$m=1-a_{ij}$
.
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is
![]() $\mathbb {Z}$
-graded as a topological
$\mathbb {Z}$
-graded as a topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra, with grading induced by the degree assignment
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra, with grading induced by the degree assignment
![]() $\deg x_{ir}^\pm =\deg h_{ir}=r$
for all
$\deg x_{ir}^\pm =\deg h_{ir}=r$
for all
![]() $i\in \mathbf {I}$
and
$i\in \mathbf {I}$
and
![]() $r\in \mathbb {Z}$
. That is, if
$r\in \mathbb {Z}$
. That is, if
![]() $\mathrm {D}Y_{\hbar }{\mathfrak {g}}_k$
denotes the closure of the subspace of
$\mathrm {D}Y_{\hbar }{\mathfrak {g}}_k$
denotes the closure of the subspace of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
spanned over the complex numbers by monomials in
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
spanned over the complex numbers by monomials in
![]() $x_{ir}^\pm $
,
$x_{ir}^\pm $
,
![]() $h_{ir}$
and
$h_{ir}$
and
![]() ${\hbar }$
of total degree k, then
${\hbar }$
of total degree k, then
is a dense,
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-subalgebra of
$\mathbb {C}[{\hbar }]$
-subalgebra of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
satisfying the conditions of Lemma 2.4. In particular, in the notation of Section 2.2, one has
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
satisfying the conditions of Lemma 2.4. In particular, in the notation of Section 2.2, one has
![]() $ {D}Y_{{\hbar }}\mathfrak {g}=\mathrm {D}Y_{\hbar }{\mathfrak {g}}_{\mathbb {Z}}$
.
$ {D}Y_{{\hbar }}\mathfrak {g}=\mathrm {D}Y_{\hbar }{\mathfrak {g}}_{\mathbb {Z}}$
.
Remark 4.2 Let
![]() $ {D}Y_{{\hbar }}\mathfrak {g}^\jmath $
denote the
$ {D}Y_{{\hbar }}\mathfrak {g}^\jmath $
denote the
![]() $\mathbb {C}[{\hbar }]$
-algebra generated by
$\mathbb {C}[{\hbar }]$
-algebra generated by
![]() $\{x_{ir}^\pm ,h_{ir}\}_{i\in \mathbf {I},r\in \mathbb {Z}}$
, subject to the defining relations (3.1)–(3.6). Then
$\{x_{ir}^\pm ,h_{ir}\}_{i\in \mathbf {I},r\in \mathbb {Z}}$
, subject to the defining relations (3.1)–(3.6). Then
![]() $ {D}Y_{{\hbar }}\mathfrak {g}^\jmath $
is a
$ {D}Y_{{\hbar }}\mathfrak {g}^\jmath $
is a
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-algebra, and there is a natural algebra homomorphism
$\mathbb {C}[{\hbar }]$
-algebra, and there is a natural algebra homomorphism
The kernel of
![]() $\jmath $
is the graded ideal
$\jmath $
is the graded ideal
![]() $\cap _{n\in \mathbb {N}}{\hbar }^n {D}Y_{{\hbar }}\mathfrak {g}^\jmath $
, and
$\cap _{n\in \mathbb {N}}{\hbar }^n {D}Y_{{\hbar }}\mathfrak {g}^\jmath $
, and
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
can be recovered as the
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
can be recovered as the
![]() ${\hbar }$
-adic completion of
${\hbar }$
-adic completion of
![]() $ {D}Y_{{\hbar }}\mathfrak {g}^\jmath $
(see [Reference Wendlandt41, Proposition 2.7]). Thus,
$ {D}Y_{{\hbar }}\mathfrak {g}^\jmath $
(see [Reference Wendlandt41, Proposition 2.7]). Thus,
![]() $\jmath ( {D}Y_{{\hbar }}\mathfrak {g}^\jmath )$
is a dense,
$\jmath ( {D}Y_{{\hbar }}\mathfrak {g}^\jmath )$
is a dense,
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-subalgebra of
$\mathbb {C}[{\hbar }]$
-subalgebra of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
. It is, however, a proper subalgebra of
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
. It is, however, a proper subalgebra of
![]() $ {D}Y_{{\hbar }}\mathfrak {g}$
as the graded components
$ {D}Y_{{\hbar }}\mathfrak {g}$
as the graded components
![]() $\jmath ( {D}Y_{{\hbar }}\mathfrak {g}^\jmath _k)$
are not closed in
$\jmath ( {D}Y_{{\hbar }}\mathfrak {g}^\jmath _k)$
are not closed in
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
. Rather, one has
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
. Rather, one has
The above definition implies that
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra deformation of the enveloping algebra
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra deformation of the enveloping algebra
![]() $U(\mathfrak {t})$
, where we recall that
$U(\mathfrak {t})$
, where we recall that
![]() $\mathfrak {t}=\mathfrak {g}[t^{\pm 1}]$
. Analogously to the Yangian case recalled in Section 3.2, the identification
$\mathfrak {t}=\mathfrak {g}[t^{\pm 1}]$
. Analogously to the Yangian case recalled in Section 3.2, the identification
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}/{\hbar }\mathrm {D}Y_{\hbar }\mathfrak {g} \cong U(\mathfrak {t})$
is induced by the graded
$\mathrm {D}Y_{\hbar }\mathfrak {g}/{\hbar }\mathrm {D}Y_{\hbar }\mathfrak {g} \cong U(\mathfrak {t})$
is induced by the graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra epimorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra epimorphism
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}\twoheadrightarrow U(\mathfrak {t})$
given by
$\mathrm {D}Y_{\hbar }\mathfrak {g}\twoheadrightarrow U(\mathfrak {t})$
given by
The Poincaré–Birkhoff–Witt theorem for
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
, established in Theorem 6.2 of [Reference Wendlandt41], asserts that
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
, established in Theorem 6.2 of [Reference Wendlandt41], asserts that
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a topologically free
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a topologically free
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module, and thus a flat deformation of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module, and thus a flat deformation of
![]() $U(\mathfrak {t})$
:
$U(\mathfrak {t})$
:
Theorem 4.3
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a flat deformation of the
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a flat deformation of the
![]() $\mathbb {Z}$
-graded algebra
$\mathbb {Z}$
-graded algebra
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}/{\hbar }\mathrm {D}Y_{\hbar }\mathfrak {g}\cong U(\mathfrak {t})$
over
$\mathrm {D}Y_{\hbar }\mathfrak {g}/{\hbar }\mathrm {D}Y_{\hbar }\mathfrak {g}\cong U(\mathfrak {t})$
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. In particular,
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. In particular,
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}\cong U(\mathfrak {t})[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as a
$\mathrm {D}Y_{\hbar }\mathfrak {g}\cong U(\mathfrak {t})[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as a
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module.
The notation for the generators of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
may seem, on the surface, to conflict with the notation used for generators in the Yangian associated with
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
may seem, on the surface, to conflict with the notation used for generators in the Yangian associated with
![]() $\mathfrak {g}$
. However, there is a natural
$\mathfrak {g}$
. However, there is a natural
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
sending each generator of
![]() $Y_{\hbar }(\mathfrak {g})\subset Y_{\hbar }\mathfrak {g}$
to the corresponding element of
$Y_{\hbar }(\mathfrak {g})\subset Y_{\hbar }\mathfrak {g}$
to the corresponding element of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
, denoted with the same symbol. By Corollary 4.4 of [Reference Wendlandt41],
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
, denoted with the same symbol. By Corollary 4.4 of [Reference Wendlandt41],
![]() $\imath $
is injective, and we shall henceforth identify
$\imath $
is injective, and we shall henceforth identify
![]() $Y_{\hbar }\mathfrak {g}$
with
$Y_{\hbar }\mathfrak {g}$
with
![]() $\imath (Y_{\hbar }\mathfrak {g})$
.
$\imath (Y_{\hbar }\mathfrak {g})$
.
4.2 Automorphisms and root vectors
To each
![]() $i\in \mathbf {I}$
, we may associate series
$i\in \mathbf {I}$
, we may associate series
![]() $\dot {x}_i^\pm (u)$
and
$\dot {x}_i^\pm (u)$
and
![]() $\dot {h}_i(u)$
in
$\dot {h}_i(u)$
in
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}[\kern-1.2pt\![u]\!\kern-1.2pt]$
by setting
$\mathrm {D}Y_{\hbar }\mathfrak {g}[\kern-1.2pt\![u]\!\kern-1.2pt]$
by setting
The following lemma is then a straightforward consequence of the defining relations of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
, where
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
, where
![]() $\omega $
and
$\omega $
and
![]() $\varsigma $
are as in Lemma 3.3.
$\varsigma $
are as in Lemma 3.3.
Lemma 4.4 There are unique extensions of the anti-automorphisms
![]() $\omega $
and
$\omega $
and
![]() $\varsigma $
of
$\varsigma $
of
![]() $Y_{\hbar }(\mathfrak {g})$
to anti-automorphisms of the
$Y_{\hbar }(\mathfrak {g})$
to anti-automorphisms of the
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
such that, for each
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
such that, for each
![]() $i\in \mathbf {I}$
,
$i\in \mathbf {I}$
,
 $$ \begin{gather*} \omega(\dot{x}_i^\pm(u))=\dot{x}_{i}^\mp(u), \quad \omega(\dot{h}_i(u))=\dot{h}_i(u),\\ \varsigma(\dot{x}_i^\pm(u))=\dot{x}_i^\pm(-u), \quad \varsigma(\dot{h}_i(u))=\dot{h}_i(-u). \end{gather*} $$
$$ \begin{gather*} \omega(\dot{x}_i^\pm(u))=\dot{x}_{i}^\mp(u), \quad \omega(\dot{h}_i(u))=\dot{h}_i(u),\\ \varsigma(\dot{x}_i^\pm(u))=\dot{x}_i^\pm(-u), \quad \varsigma(\dot{h}_i(u))=\dot{h}_i(-u). \end{gather*} $$
Following the terminology from Section 3.3, we shall refer to the involution
![]() $\omega $
as the Chevalley involution of
$\omega $
as the Chevalley involution of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
.
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
.
The adjoint action of
![]() $\mathfrak {h}\subset \mathrm {D}Y_{\hbar }\mathfrak {g}$
on
$\mathfrak {h}\subset \mathrm {D}Y_{\hbar }\mathfrak {g}$
on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
gives rise to a topological Q-grading on the
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
gives rise to a topological Q-grading on the
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
(cf. Corollary 6.5 and [Reference Wendlandt41, Section 3.1]) with graded components given by the weight spaces
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
(cf. Corollary 6.5 and [Reference Wendlandt41, Section 3.1]) with graded components given by the weight spaces
That is to say, each of these subspaces is a closed
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-submodule of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-submodule of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
, and the direct sum
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
, and the direct sum
is a Q-graded dense
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-subalgebra of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-subalgebra of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
whose subspace topology coincides with its
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
whose subspace topology coincides with its
![]() ${\hbar }$
-adic topology. Here, we have borrowed, and modified appropriately, the terminology of Section 2.2. It should be emphasized that the word topological is key in this statement, as the Q-graded algebra
${\hbar }$
-adic topology. Here, we have borrowed, and modified appropriately, the terminology of Section 2.2. It should be emphasized that the word topological is key in this statement, as the Q-graded algebra
![]() $\mathrm {D}Y_{\hbar }{\mathfrak {g}}_Q$
is a proper subset of
$\mathrm {D}Y_{\hbar }{\mathfrak {g}}_Q$
is a proper subset of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
.
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
.
We now introduce root vectors in
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
of arbitrary degree, following the procedure used in Section 3.4. Recall from (3.11) that to each positive root
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
of arbitrary degree, following the procedure used in Section 3.4. Recall from (3.11) that to each positive root
![]() $\beta \in \Delta ^+$
, we attached an index
$\beta \in \Delta ^+$
, we attached an index
![]() $i(\beta )\in \mathbf {I}$
and an element
$i(\beta )\in \mathbf {I}$
and an element
![]() $\mathbf {X}^\beta \in U({\mathfrak {n}}_{+})_{\beta -\alpha _{i(\beta )}}$
. For each
$\mathbf {X}^\beta \in U({\mathfrak {n}}_{+})_{\beta -\alpha _{i(\beta )}}$
. For each
![]() $k\in \mathbb {Z}$
, we then set
$k\in \mathbb {Z}$
, we then set
where
![]() $\mathfrak {g}$
operates on
$\mathfrak {g}$
operates on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
via the adjoint action. For
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
via the adjoint action. For
![]() $k\in \mathbb {N}$
, these elements are identical to those introduced below (3.11). Moreover, we have
$k\in \mathbb {N}$
, these elements are identical to those introduced below (3.11). Moreover, we have
It shall be convenient for us to organize the above elements into generating series
![]() $x_\beta ^\pm (u)\in \mathrm {D}Y_{\hbar }{\mathfrak {g}}_{\pm \beta }[\kern-1.2pt\![u^{-1}]\!\kern-1.2pt]$
and
$x_\beta ^\pm (u)\in \mathrm {D}Y_{\hbar }{\mathfrak {g}}_{\pm \beta }[\kern-1.2pt\![u^{-1}]\!\kern-1.2pt]$
and
![]() $\dot {x}_\beta ^\pm (u)\in \mathrm {D}Y_{\hbar }{\mathfrak {g}}_{\pm \beta }[\kern-1.2pt\![u]\!\kern-1.2pt]$
by setting
$\dot {x}_\beta ^\pm (u)\in \mathrm {D}Y_{\hbar }{\mathfrak {g}}_{\pm \beta }[\kern-1.2pt\![u]\!\kern-1.2pt]$
by setting
4.3 The formal shift operator
We now shift our attention to recalling some of the main constructions of [Reference Wendlandt41], subject to our standing assumption that
![]() $\mathfrak {g}$
is a finite-dimensional simple Lie algebra. To begin, we introduce a number of relevant spaces built from the Yangian
$\mathfrak {g}$
is a finite-dimensional simple Lie algebra. To begin, we introduce a number of relevant spaces built from the Yangian
![]() $Y_{\hbar }(\mathfrak {g})$
, following Sections 4.1 and 4.2 of [Reference Wendlandt41] and Section 3.6 above. First, let
$Y_{\hbar }(\mathfrak {g})$
, following Sections 4.1 and 4.2 of [Reference Wendlandt41] and Section 3.6 above. First, let
denote the formal completion of
![]() $Y_{\hbar }(\mathfrak {g})$
with respect to its
$Y_{\hbar }(\mathfrak {g})$
with respect to its
![]() $\mathbb {N}$
-grading. This is a topologically free
$\mathbb {N}$
-grading. This is a topologically free
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra containing
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra containing
![]() $Y_{\hbar }\mathfrak {g}$
as a subalgebra (see [Reference Gautam and Toledano Laredo15, Proposition 6.3] or [Reference Wendlandt41, Lemma 4.1]).
$Y_{\hbar }\mathfrak {g}$
as a subalgebra (see [Reference Gautam and Toledano Laredo15, Proposition 6.3] or [Reference Wendlandt41, Lemma 4.1]).
Next, let
![]() $ {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
and
$ {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
and
![]() $\widehat {Y_{\hbar }\mathfrak {g}}_z$
denote the subspaces
$\widehat {Y_{\hbar }\mathfrak {g}}_z$
denote the subspaces
![]() $ {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(1)}}_z)$
and
$ {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(1)}}_z)$
and
![]() $\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(1)}}_z$
of the space of Laurent series
$\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(1)}}_z$
of the space of Laurent series
![]() $Y_{\hbar }(\mathfrak {g})[z;z^{-1}]\!\kern-1.2pt]$
introduced in Section 3.6. That is,
$Y_{\hbar }(\mathfrak {g})[z;z^{-1}]\!\kern-1.2pt]$
introduced in Section 3.6. That is,
and
![]() $ {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
is the
$ {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
is the
![]() $\mathbb {Z}$
-graded subalgebra of
$\mathbb {Z}$
-graded subalgebra of
![]() $Y_{\hbar }(\mathfrak {g})[z;z^{-1}]\!\kern-1.2pt]$
over
$Y_{\hbar }(\mathfrak {g})[z;z^{-1}]\!\kern-1.2pt]$
over
![]() $\mathbb {C}[{\hbar }]$
defined by
$\mathbb {C}[{\hbar }]$
defined by
The following lemma, established in [Reference Wendlandt41, Proposition 4.2], provides a characterization of the
![]() ${\hbar }$
-adic completion of
${\hbar }$
-adic completion of
![]() $ {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
.
$ {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
.
Lemma 4.5 The
![]() ${\hbar }$
-adic completion
${\hbar }$
-adic completion
![]() $\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
of
$\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
of
![]() $ {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
is the subspace of
$ {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
is the subspace of
![]() $Y_{\hbar }\mathfrak {g}[\kern-1.2pt\![z^{\pm 1}]\!\kern-1.2pt]$
consisting of formal series
$Y_{\hbar }\mathfrak {g}[\kern-1.2pt\![z^{\pm 1}]\!\kern-1.2pt]$
consisting of formal series
with the property that, for each
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $\exists \ N_n\in \mathbb {N}$
such that
$\exists \ N_n\in \mathbb {N}$
such that
Moreover,
![]() $\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
is a topologically free
$\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
is a topologically free
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra with
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra with
The last statement of the lemma employs the notation from Lemma 2.4 and follows from the fact that
![]() $ {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
is a torsion-free
$ {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
is a torsion-free
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-algebra and that each subspace
$\mathbb {C}[{\hbar }]$
-algebra and that each subspace
![]() $z^k\widehat {Y_{\hbar }\mathfrak {g}}_z$
is closed in
$z^k\widehat {Y_{\hbar }\mathfrak {g}}_z$
is closed in
![]() $Y_{\hbar }\mathfrak {g}[\kern-1.2pt\![z^{\pm 1}]\!\kern-1.2pt]$
, equipped with the
$Y_{\hbar }\mathfrak {g}[\kern-1.2pt\![z^{\pm 1}]\!\kern-1.2pt]$
, equipped with the
![]() ${\hbar }$
-adic topology, and thus in
${\hbar }$
-adic topology, and thus in
![]() $\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
.
$\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
.
Next, recall that
![]() $\tau _z$
is the formal shift homomorphism of the Yangian introduced in (3.8), which we may view as a
$\tau _z$
is the formal shift homomorphism of the Yangian introduced in (3.8), which we may view as a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
In addition, we set
![]() $\partial _z^{(n)}=\frac {1}{n!}\partial _z^n$
for each
$\partial _z^{(n)}=\frac {1}{n!}\partial _z^n$
for each
![]() $n\in \mathbb {N}$
, where
$n\in \mathbb {N}$
, where
![]() $\partial _z$
is the partial derivative operator with respect to z. The following theorem, which is a combination of a special case of Theorems 4.3 and 6.2 of [Reference Wendlandt41], introduces the so-called formal shift operator
$\partial _z$
is the partial derivative operator with respect to z. The following theorem, which is a combination of a special case of Theorems 4.3 and 6.2 of [Reference Wendlandt41], introduces the so-called formal shift operator
![]() $\Phi _z$
on
$\Phi _z$
on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
.
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
.
Theorem 4.6 There is a unique homomorphism of
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras
with the property that
![]() $\Phi _z\circ \imath =\tau _z$
. Moreover:
$\Phi _z\circ \imath =\tau _z$
. Moreover:
-
(1)
 $\Phi _z$
is injective, and satisfies
$\Phi _z$
is injective, and satisfies  $$ \begin{align*} \Phi_z(\dot{x}_\beta^\pm(u))&=\sum_{n\in \mathbb{N}}(-1)^{n}u^n \partial_z^{(n)} x_\beta^\pm(-z) \quad \forall \;\beta\in \Delta^+,\\ \Phi_z(\dot{h}_i(u))&=\sum_{n\in \mathbb{N}}(-1)^{n}u^n \partial_z^{(n)} h_i(-z) \quad \forall \; i\in \mathbf{I}. \end{align*} $$
$$ \begin{align*} \Phi_z(\dot{x}_\beta^\pm(u))&=\sum_{n\in \mathbb{N}}(-1)^{n}u^n \partial_z^{(n)} x_\beta^\pm(-z) \quad \forall \;\beta\in \Delta^+,\\ \Phi_z(\dot{h}_i(u))&=\sum_{n\in \mathbb{N}}(-1)^{n}u^n \partial_z^{(n)} h_i(-z) \quad \forall \; i\in \mathbf{I}. \end{align*} $$
-
(2) The restriction of
 $\Phi _z$
to
$\Phi _z$
to
 $ {D}Y_{{\hbar }}\mathfrak {g}$
is a
$ {D}Y_{{\hbar }}\mathfrak {g}$
is a
 $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
 $\mathbb {C}[{\hbar }]$
-algebra homomorphism
$\mathbb {C}[{\hbar }]$
-algebra homomorphism  $$ \begin{align*} \Phi_z|_{{D}Y_{{\hbar}}\mathfrak{g}}: {D}Y_{{\hbar}}\mathfrak{g}\to {L}\widehat{Y_{\hbar}\mathfrak{g}}_z=\bigoplus_{n\in \mathbb{Z}}z^n \widehat{Y_{\hbar}\mathfrak{g}}_z \subset Y_{\hbar}(\mathfrak{g})[z;z^{-1}]\!\kern-1.2pt]. \end{align*} $$
$$ \begin{align*} \Phi_z|_{{D}Y_{{\hbar}}\mathfrak{g}}: {D}Y_{{\hbar}}\mathfrak{g}\to {L}\widehat{Y_{\hbar}\mathfrak{g}}_z=\bigoplus_{n\in \mathbb{Z}}z^n \widehat{Y_{\hbar}\mathfrak{g}}_z \subset Y_{\hbar}(\mathfrak{g})[z;z^{-1}]\!\kern-1.2pt]. \end{align*} $$
Remark 4.7 In the terminology of Section 2.2, Part (2) is equivalent to the assertion that
![]() $\Phi _z$
is a
$\Phi _z$
is a
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism. This is implied by Part (2) of Theorem 4.3 in [Reference Wendlandt41], which asserts that the composition
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism. This is implied by Part (2) of Theorem 4.3 in [Reference Wendlandt41], which asserts that the composition
![]() $\Phi _z\circ \jmath $
is a
$\Phi _z\circ \jmath $
is a
![]() $\mathbb {Z}$
-graded algebra homomorphism, where
$\mathbb {Z}$
-graded algebra homomorphism, where
![]() $\jmath $
is as in Remark 4.2.
$\jmath $
is as in Remark 4.2.
By [Reference Wendlandt41, Proposition 4.2(4)], the evaluation map
is an epimorphism of
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras. We may thus compose
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras. We may thus compose
![]() $\Phi _z$
with
$\Phi _z$
with
![]() $\mathscr{E}\mathscr{v}$
to obtain a
$\mathscr{E}\mathscr{v}$
to obtain a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
By Theorem 6.2 of [Reference Wendlandt41], this homomorphism is injective. One of the main results of [Reference Wendlandt41] is that
![]() $\Phi $
induces an isomorphism between completions of
$\Phi $
induces an isomorphism between completions of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
of
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
of
![]() $Y_{\hbar }(\mathfrak {g})$
. To make this precise, let
$Y_{\hbar }(\mathfrak {g})$
. To make this precise, let
![]() $\mathcal {J}\subset \mathrm {D}Y_{\hbar }\mathfrak {g}$
denote the kernel of the composition
$\mathcal {J}\subset \mathrm {D}Y_{\hbar }\mathfrak {g}$
denote the kernel of the composition
and define
![]() $\widehat {\mathrm {D}Y_{\hbar }\mathfrak {g}}$
to be the completion of
$\widehat {\mathrm {D}Y_{\hbar }\mathfrak {g}}$
to be the completion of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
with respect to the
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
with respect to the
![]() $\mathcal {J}$
-adic filtration
$\mathcal {J}$
-adic filtration
We then have the following analogue of [Reference Gautam and Toledano Laredo15, Theorem 6.2], which is a special case of Theorem 5.5 in [Reference Wendlandt41].
Theorem 4.8
![]() $\Phi $
is injective and induces an isomorphism of
$\Phi $
is injective and induces an isomorphism of
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras
with inverse
![]() $\Gamma $
uniquely extending the embedding
$\Gamma $
uniquely extending the embedding
![]() $\imath \circ \tau _{-1}:Y_{\hbar }(\mathfrak {g})\to \mathrm {D}Y_{\hbar }\mathfrak {g}$
.
$\imath \circ \tau _{-1}:Y_{\hbar }(\mathfrak {g})\to \mathrm {D}Y_{\hbar }\mathfrak {g}$
.
Remark 4.9 One subtle consequence of this result is that the natural homomorphism
is injective. Indeed, its composition with the isomorphism
![]() $\widehat {\Phi }$
recovers the injection
$\widehat {\Phi }$
recovers the injection
![]() $\Phi $
. Henceforth, we shall freely make use of this fact and view
$\Phi $
. Henceforth, we shall freely make use of this fact and view
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
as a subalgebra of
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
as a subalgebra of
![]() $\widehat {\mathrm {D}Y_{\hbar }\mathfrak {g}}$
. We further note that the subspace topology on
$\widehat {\mathrm {D}Y_{\hbar }\mathfrak {g}}$
. We further note that the subspace topology on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
, with respect to the
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
, with respect to the
![]() ${\hbar }$
-adic topology on
${\hbar }$
-adic topology on
![]() $\widehat {\mathrm {D}Y_{\hbar }\mathfrak {g}}$
, coincides with the
$\widehat {\mathrm {D}Y_{\hbar }\mathfrak {g}}$
, coincides with the
![]() ${\hbar }$
-adic topology on
${\hbar }$
-adic topology on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
. Indeed, as
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
. Indeed, as
![]() $\widehat {\mathrm {D}Y_{\hbar }\mathfrak {g}}\cong \widehat {Y_{\hbar }\mathfrak {g}}$
is torsion-free, to see this it suffices to show that
$\widehat {\mathrm {D}Y_{\hbar }\mathfrak {g}}\cong \widehat {Y_{\hbar }\mathfrak {g}}$
is torsion-free, to see this it suffices to show that
This, however, follows immediately from the injectivity of the semiclassical limit of
![]() $\Phi $
, established in [Reference Wendlandt41, Theorem 6.2]. In particular, this discussion implies that
$\Phi $
, established in [Reference Wendlandt41, Theorem 6.2]. In particular, this discussion implies that
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a closed subspace of the topological
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a closed subspace of the topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module
![]() $\widehat {\mathrm {D}Y_{\hbar }\mathfrak {g}}$
. Similarly, one deduces that
$\widehat {\mathrm {D}Y_{\hbar }\mathfrak {g}}$
. Similarly, one deduces that
![]() $\Phi _z(\mathrm {D}Y_{\hbar }\mathfrak {g})$
is a closed subspace of
$\Phi _z(\mathrm {D}Y_{\hbar }\mathfrak {g})$
is a closed subspace of
![]() $\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
.
$\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
.
To conclude this preliminary section on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
, we introduce the auxiliary
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
, we introduce the auxiliary
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
which has the property that
![]() $\Gamma _z|_{\mathrm {Im}(\Phi _z)}=\Phi _z^{-1}$
. This homomorphism shall play a prominent role in the main result of Section 7 and its proof (see Theorem 7.5).
$\Gamma _z|_{\mathrm {Im}(\Phi _z)}=\Phi _z^{-1}$
. This homomorphism shall play a prominent role in the main result of Section 7 and its proof (see Theorem 7.5).
5 The Drinfeld–Gavarini Yangian
In this section and Section 6, we give a self-contained exposition to the dual Yangian
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
, which provides a homogeneous quantization of the graded dual
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
, which provides a homogeneous quantization of the graded dual
![]() ${\mathfrak {t}}_{\scriptscriptstyle {-}}=t^{-1}\mathfrak {g}[t^{-1}]$
to the Lie bialgebra
${\mathfrak {t}}_{\scriptscriptstyle {-}}=t^{-1}\mathfrak {g}[t^{-1}]$
to the Lie bialgebra
![]() ${\mathfrak {t}}_{\scriptscriptstyle {+}}=\mathfrak {g}[t]$
, as will be explained in detail in Section 6. The definition of
${\mathfrak {t}}_{\scriptscriptstyle {+}}=\mathfrak {g}[t]$
, as will be explained in detail in Section 6. The definition of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
takes as input the so-called Drinfeld–Gavarini subalgebra of the Yangian. The goal of the present section is to introduce this subalgebra and survey some of its key properties.
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
takes as input the so-called Drinfeld–Gavarini subalgebra of the Yangian. The goal of the present section is to introduce this subalgebra and survey some of its key properties.
5.1 Quantum duality
To provide context, let us first briefly recall the general construction of the dual of a quantized enveloping algebra, following [Reference Drinfel’d7, Section 7] and [Reference Gavarini19, Section 4.4] (see also [Reference Etingof and Kazhdan11] and [Reference Appel and Toledano Laredo1, Section 2.19], for example).
Suppose that
![]() $U_{\hbar }\mathfrak {b}$
is a quantization of a finite-dimensional Lie bialgebra
$U_{\hbar }\mathfrak {b}$
is a quantization of a finite-dimensional Lie bialgebra
![]() $(\mathfrak {b},\delta _{\mathfrak {b}})$
, where we follow the terminology and notation from Section 2.4. One would then like to introduce a notion of duality which sends
$(\mathfrak {b},\delta _{\mathfrak {b}})$
, where we follow the terminology and notation from Section 2.4. One would then like to introduce a notion of duality which sends
![]() $U_{\hbar }\mathfrak {b}$
to a quantization of the Lie bialgebra dual
$U_{\hbar }\mathfrak {b}$
to a quantization of the Lie bialgebra dual
![]() $({\mathfrak {b}}^\ast , \delta _{{\mathfrak {b}}^\ast }=[\,,\,]_{\mathfrak {b}}^\ast )$
to
$({\mathfrak {b}}^\ast , \delta _{{\mathfrak {b}}^\ast }=[\,,\,]_{\mathfrak {b}}^\ast )$
to
![]() $(\mathfrak {b},\delta _{\mathfrak {b}})$
. The first crucial observation is that
$(\mathfrak {b},\delta _{\mathfrak {b}})$
. The first crucial observation is that
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear dual
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear dual
![]() $U_{\hbar }{\mathfrak {b}}^\ast =\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}(U_{\hbar }\mathfrak {b},\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])$
of
$U_{\hbar }{\mathfrak {b}}^\ast =\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}(U_{\hbar }\mathfrak {b},\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])$
of
![]() $U_{\hbar }\mathfrak {b}$
is not itself a quantized enveloping algebra (see Lemma 2.1 of [Reference Gavarini19], in addition to [Reference Drinfel’d7, Section 7] and [Reference Appel and Toledano Laredo1, Section 2.19]). The correct notion of duality within the category of quantized enveloping algebras was introduced in [Reference Drinfel’d7, Section 7]. One considers the
$U_{\hbar }\mathfrak {b}$
is not itself a quantized enveloping algebra (see Lemma 2.1 of [Reference Gavarini19], in addition to [Reference Drinfel’d7, Section 7] and [Reference Appel and Toledano Laredo1, Section 2.19]). The correct notion of duality within the category of quantized enveloping algebras was introduced in [Reference Drinfel’d7, Section 7]. One considers the
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-submodule
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-submodule
where
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $\Delta $
are the counit and coproduct, respectively, on the topological Hopf algebra
$\Delta $
are the counit and coproduct, respectively, on the topological Hopf algebra
![]() $U_{\hbar }\mathfrak {b}$
, and all notation is as in Section 5.2 below. Then, by [Reference Gavarini19, Proposition 3.6],
$U_{\hbar }\mathfrak {b}$
, and all notation is as in Section 5.2 below. Then, by [Reference Gavarini19, Proposition 3.6],
![]() $U_{\hbar }{\mathfrak {b}}^\prime $
is a quantized formal series Hopf algebra, with semiclassical limit isomorphic as an algebra to the completion of the symmetric algebra
$U_{\hbar }{\mathfrak {b}}^\prime $
is a quantized formal series Hopf algebra, with semiclassical limit isomorphic as an algebra to the completion of the symmetric algebra
![]() $\mathsf {S}(\mathfrak {b})=\bigoplus _{n\in \mathbb {N}} \mathsf {S}^n(\mathfrak {b})$
with respect to its standard grading. In particular, this means that although
$\mathsf {S}(\mathfrak {b})=\bigoplus _{n\in \mathbb {N}} \mathsf {S}^n(\mathfrak {b})$
with respect to its standard grading. In particular, this means that although
![]() $U_{\hbar }{\mathfrak {b}}^\prime $
is not in general a topological Hopf algebra over
$U_{\hbar }{\mathfrak {b}}^\prime $
is not in general a topological Hopf algebra over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
in the sense of Section 2.1, it is a topological Hopf algebra with respect to the
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
in the sense of Section 2.1, it is a topological Hopf algebra with respect to the
![]() $\mathbf {J}_{\mathfrak {b}}$
-adic topology, where
$\mathbf {J}_{\mathfrak {b}}$
-adic topology, where
The subspace
![]() $ U_{\hbar }{\mathfrak {b}}^{\circ }\subset (U_{\hbar }{\mathfrak {b}}^\prime )^\ast $
consisting of continuous linear forms with respect to this topology is then a quantization of
$ U_{\hbar }{\mathfrak {b}}^{\circ }\subset (U_{\hbar }{\mathfrak {b}}^\prime )^\ast $
consisting of continuous linear forms with respect to this topology is then a quantization of
![]() $({\mathfrak {b}}^\ast , \delta _{{\mathfrak {b}}^\ast })$
. This is the quantized enveloping algebra dual of
$({\mathfrak {b}}^\ast , \delta _{{\mathfrak {b}}^\ast })$
. This is the quantized enveloping algebra dual of
![]() $U_{\hbar }\mathfrak {b}$
.
$U_{\hbar }\mathfrak {b}$
.
Remark 5.1 Here, we note that
![]() $U_{\hbar }{\mathfrak {b}}^{\circ }$
can be equivalently defined as the
$U_{\hbar }{\mathfrak {b}}^{\circ }$
can be equivalently defined as the
![]() ${\hbar }$
-adic completion of the
${\hbar }$
-adic completion of the
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module
where
![]() ${\mathfrak {m}}_{\mathfrak {b}}:=\{f\in U_{\hbar }{\mathfrak {b}}^\ast : f(1)\in {\hbar }\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]\}$
. That this produces a topological Hopf algebra which can be identified with
${\mathfrak {m}}_{\mathfrak {b}}:=\{f\in U_{\hbar }{\mathfrak {b}}^\ast : f(1)\in {\hbar }\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]\}$
. That this produces a topological Hopf algebra which can be identified with
![]() $U_{\hbar }{\mathfrak {b}}^{\circ }$
is a nontrivial result, which is part of the quantum duality principle. This was first announced in [Reference Drinfel’d7, Section 7], and proven in detail in [Reference Gavarini19] (see Theorem 1.6 therein). We will not, however, need this equivalent formulation in the present article.
$U_{\hbar }{\mathfrak {b}}^{\circ }$
is a nontrivial result, which is part of the quantum duality principle. This was first announced in [Reference Drinfel’d7, Section 7], and proven in detail in [Reference Gavarini19] (see Theorem 1.6 therein). We will not, however, need this equivalent formulation in the present article.
In our setting,
![]() $\mathfrak {b}={\mathfrak {t}}_{\scriptscriptstyle {+}}=\mathfrak {g}[t]$
is not finite-dimensional, but rather an
$\mathfrak {b}={\mathfrak {t}}_{\scriptscriptstyle {+}}=\mathfrak {g}[t]$
is not finite-dimensional, but rather an
![]() $\mathbb {N}$
-graded Lie bialgebra
$\mathbb {N}$
-graded Lie bialgebra
![]() $\mathfrak {b}=\bigoplus _{n\in \mathbb {N}}\mathfrak {b}_n$
with finite-dimensional graded components. As
$\mathfrak {b}=\bigoplus _{n\in \mathbb {N}}\mathfrak {b}_n$
with finite-dimensional graded components. As
![]() $Y_{\hbar }\mathfrak {g}=U_{\hbar }\mathfrak {b}$
is a homogeneous quantization of
$Y_{\hbar }\mathfrak {g}=U_{\hbar }\mathfrak {b}$
is a homogeneous quantization of
![]() ${\mathfrak {t}}_{\scriptscriptstyle {+}}$
, the above construction remains valid, provided the notion of duality is adjusted so as to respect the underlying gradings. In fact, one can replace
${\mathfrak {t}}_{\scriptscriptstyle {+}}$
, the above construction remains valid, provided the notion of duality is adjusted so as to respect the underlying gradings. In fact, one can replace
![]() $U_{\hbar }{\mathfrak {b}}^\prime $
with an
$U_{\hbar }{\mathfrak {b}}^\prime $
with an
![]() $\mathbb {N}$
-graded topological Hopf algebra
$\mathbb {N}$
-graded topological Hopf algebra
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
over
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
of finite type, and
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
of finite type, and
![]() $U_{\hbar }{\mathfrak {b}}^\circ $
with the restricted dual of
$U_{\hbar }{\mathfrak {b}}^\circ $
with the restricted dual of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
, as defined in Section 2.3. The topological Hopf algebra
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
, as defined in Section 2.3. The topological Hopf algebra
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
and its
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
and its
![]() $\mathbb {C}[{\hbar }]$
-form
$\mathbb {C}[{\hbar }]$
-form
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})=({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g})_{\mathbb {N}}$
(see Section 2.2) are the focus of the present section.
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})=({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g})_{\mathbb {N}}$
(see Section 2.2) are the focus of the present section.
5.2 The Drinfeld–Gavarini subalgebra
Let us define
![]() $\Delta ^n$
for any
$\Delta ^n$
for any
![]() $n\in \mathbb {N}$
by setting
$n\in \mathbb {N}$
by setting
![]() $\Delta ^0=\varepsilon $
,
$\Delta ^0=\varepsilon $
,
![]() $\Delta ^1=\mathbf {1}=\mathbf {1}_{Y_{\hbar }(\mathfrak {g})}$
and
$\Delta ^1=\mathbf {1}=\mathbf {1}_{Y_{\hbar }(\mathfrak {g})}$
and
for all
![]() $n\geq 2$
. We then define the
$n\geq 2$
. We then define the
![]() $\mathbb {C}[{\hbar }]$
-submodule
$\mathbb {C}[{\hbar }]$
-submodule
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\subset Y_{\hbar }(\mathfrak {g})$
by
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\subset Y_{\hbar }(\mathfrak {g})$
by
By Lemma 3.2 and Proposition 3.5 of [Reference Kassel and Turaev27] (see also [Reference Gavarini19, Proposition 2.6], [Reference Gavarini20, Theorem 3.5], and [Reference Finkelberg and Tsymbaliuk13, Lemma A.1]),
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is a subalgebra of
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is a subalgebra of
![]() $Y_{\hbar }(\mathfrak {g})$
which is commutative modulo
$Y_{\hbar }(\mathfrak {g})$
which is commutative modulo
![]() ${\hbar }$
:
${\hbar }$
:
As the structure maps
![]() $\mathbf {1}$
,
$\mathbf {1}$
,
![]() $\varepsilon $
, and
$\varepsilon $
, and
![]() $\Delta ^n$
are graded,
$\Delta ^n$
are graded,
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
inherits from
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
inherits from
![]() $Y_{\hbar }(\mathfrak {g})$
the structure of an
$Y_{\hbar }(\mathfrak {g})$
the structure of an
![]() $\mathbb {N}$
-graded algebra. We shall call
$\mathbb {N}$
-graded algebra. We shall call
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
the Drinfeld–Gavarini subalgebra of the Yangian
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
the Drinfeld–Gavarini subalgebra of the Yangian
![]() $Y_{\hbar }(\mathfrak {g})$
. Its algebraic structure has been described in detail by Tsymbaliuk and Weekes in Appendix Appendix A of [Reference Finkelberg and Tsymbaliuk13], following the general results obtained in the works [Reference Gavarini19, Reference Gavarini20] of Gavarini. In this subsection, we review, and partially extend, this description.
$Y_{\hbar }(\mathfrak {g})$
. Its algebraic structure has been described in detail by Tsymbaliuk and Weekes in Appendix Appendix A of [Reference Finkelberg and Tsymbaliuk13], following the general results obtained in the works [Reference Gavarini19, Reference Gavarini20] of Gavarini. In this subsection, we review, and partially extend, this description.
Let
![]() $\mathsf {R}_{\hbar }(U({\mathfrak {t}}_{\scriptscriptstyle {+}}))$
denote the Rees algebra associated with the standard enveloping algebra filtration
$\mathsf {R}_{\hbar }(U({\mathfrak {t}}_{\scriptscriptstyle {+}}))$
denote the Rees algebra associated with the standard enveloping algebra filtration
![]() ${\mathbf {F}}_\bullet $
on
${\mathbf {F}}_\bullet $
on
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
:
$U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
:
Consider now the symmetric algebra
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})\subset \mathsf {S}({\mathfrak {t}}_{\scriptscriptstyle {+}})[{\hbar }]$
on
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})\subset \mathsf {S}({\mathfrak {t}}_{\scriptscriptstyle {+}})[{\hbar }]$
on
![]() ${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}$
. Here,
${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}$
. Here,
![]() ${\hbar }$
can be viewed as a gradation parameter associated with the standard
${\hbar }$
can be viewed as a gradation parameter associated with the standard
![]() $\mathbb {N}$
-grading on the symmetric algebra
$\mathbb {N}$
-grading on the symmetric algebra
![]() $\mathsf {S}({\mathfrak {t}}_{\scriptscriptstyle {+}})$
. Namely,
$\mathsf {S}({\mathfrak {t}}_{\scriptscriptstyle {+}})$
. Namely,
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})\cap {\hbar }^n\mathsf {S}({\mathfrak {t}}_{\scriptscriptstyle {+}})$
is precisely the nth symmetric power
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})\cap {\hbar }^n\mathsf {S}({\mathfrak {t}}_{\scriptscriptstyle {+}})$
is precisely the nth symmetric power
![]() $\mathsf {S}^{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})={\hbar }^n\mathsf {S}^n({\mathfrak {t}}_{\scriptscriptstyle {+}})$
, and
$\mathsf {S}^{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})={\hbar }^n\mathsf {S}^n({\mathfrak {t}}_{\scriptscriptstyle {+}})$
, and
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})\cong \mathsf {S}({\mathfrak {t}}_{\scriptscriptstyle {+}})$
as an
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})\cong \mathsf {S}({\mathfrak {t}}_{\scriptscriptstyle {+}})$
as an
![]() $\mathbb {N}$
-graded algebra. As
$\mathbb {N}$
-graded algebra. As
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
is a filtered deformation of
$U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
is a filtered deformation of
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
(that is, one has
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
(that is, one has
![]() $\mathrm {gr}\,U({\mathfrak {t}}_{\scriptscriptstyle {+}})\cong \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
),
$\mathrm {gr}\,U({\mathfrak {t}}_{\scriptscriptstyle {+}})\cong \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
),
![]() $\mathsf {R}_{\hbar }(U({\mathfrak {t}}_{\scriptscriptstyle {+}}))$
is a flat deformation of
$\mathsf {R}_{\hbar }(U({\mathfrak {t}}_{\scriptscriptstyle {+}}))$
is a flat deformation of
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
over
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
over
![]() $\mathbb {C}[{\hbar }]$
. Let
$\mathbb {C}[{\hbar }]$
. Let
be the natural quotient map, under the identification of
![]() $\mathsf {R}_{\hbar }(U({\mathfrak {t}}_{\scriptscriptstyle {+}}))/{\hbar }\mathsf {R}_{\hbar }(U({\mathfrak {t}}_{\scriptscriptstyle {+}}))$
with
$\mathsf {R}_{\hbar }(U({\mathfrak {t}}_{\scriptscriptstyle {+}}))/{\hbar }\mathsf {R}_{\hbar }(U({\mathfrak {t}}_{\scriptscriptstyle {+}}))$
with
![]() $ \mathrm {gr}\,U({\mathfrak {t}}_{\scriptscriptstyle {+}})\cong \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
. In what follows, we shall be primarily interested in the loop gradings on
$ \mathrm {gr}\,U({\mathfrak {t}}_{\scriptscriptstyle {+}})\cong \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
. In what follows, we shall be primarily interested in the loop gradings on
![]() $\mathsf {R}_{\hbar }(U({\mathfrak {t}}_{\scriptscriptstyle {+}}))$
and
$\mathsf {R}_{\hbar }(U({\mathfrak {t}}_{\scriptscriptstyle {+}}))$
and
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
, inherited from the natural grading on
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
, inherited from the natural grading on
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {+}})[{\hbar }]$
compatible with the
$U({\mathfrak {t}}_{\scriptscriptstyle {+}})[{\hbar }]$
compatible with the
![]() $\mathbb {N}$
-grading on
$\mathbb {N}$
-grading on
![]() ${\mathfrak {t}}_{\scriptscriptstyle {+}}$
. Namely, one has
${\mathfrak {t}}_{\scriptscriptstyle {+}}$
. Namely, one has
We shall denote the nth graded component of
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
by
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
by
![]() $\mathsf {S}_{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
so that
$\mathsf {S}_{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
so that
Recall from Section 3.4 that
![]() $\unicode{x3bd} _{ {G}}$
denotes the graded
$\unicode{x3bd} _{ {G}}$
denotes the graded
![]() $\mathbb {C}[{\hbar }]$
-module isomorphism
$\mathbb {C}[{\hbar }]$
-module isomorphism
defined in (3.12), which depends on a fixed total order on the set
![]() $ {G}$
. We equip
$ {G}$
. We equip
![]() ${\hbar } {G}$
with the induced ordering, for which multiplication by
${\hbar } {G}$
with the induced ordering, for which multiplication by
![]() ${\hbar }$
defines an isomorphism of ordered sets
${\hbar }$
defines an isomorphism of ordered sets ![]() , and we let
, and we let
![]() $B({\hbar } {G})\subset Y_{\hbar }(\mathfrak {g})$
denote the corresponding set of ordered monomials in
$B({\hbar } {G})\subset Y_{\hbar }(\mathfrak {g})$
denote the corresponding set of ordered monomials in
![]() ${\hbar } {G}$
. We further recall that
${\hbar } {G}$
. We further recall that
![]() $\mu :U({\mathfrak {t}}_{\scriptscriptstyle {+}})[{\hbar }]\to Y_{\hbar }(\mathfrak {g})$
is the inverse of the specific choice
$\mu :U({\mathfrak {t}}_{\scriptscriptstyle {+}})[{\hbar }]\to Y_{\hbar }(\mathfrak {g})$
is the inverse of the specific choice
![]() $\unicode{x3bd} =\unicode{x3bd} _{ {G}}$
defined in (3.13).
$\unicode{x3bd} =\unicode{x3bd} _{ {G}}$
defined in (3.13).
The following proposition is a consequence of Proposition 3.3 of [Reference Gavarini20] in addition to Proposition A.2 and Theorem A.7 of [Reference Finkelberg and Tsymbaliuk13] (see also [Reference Gavarini19, Section 3.5]).
Proposition 5.2 Let
![]() $\dot {\unicode{x3bd} }_{ {G}}$
denote the restriction of
$\dot {\unicode{x3bd} }_{ {G}}$
denote the restriction of
![]() $\unicode{x3bd} _{ {G}}$
to
$\unicode{x3bd} _{ {G}}$
to
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
. Then:
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
. Then:
-
(1)
 ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is an
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is an
 $\mathbb {N}$
-graded Hopf subalgebra of
$\mathbb {N}$
-graded Hopf subalgebra of
 $Y_{\hbar }(\mathfrak {g})$
.
$Y_{\hbar }(\mathfrak {g})$
. -
(2)
 $\dot {\unicode{x3bd} }_{ {G}}$
is an isomorphism of
$\dot {\unicode{x3bd} }_{ {G}}$
is an isomorphism of
 $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
 $\mathbb {C}[{\hbar }]$
-modules
$\mathbb {C}[{\hbar }]$
-modules 
-
(3)
 ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is generated as a
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is generated as a
 $\mathbb {C}[{\hbar }]$
-algebra by
$\mathbb {C}[{\hbar }]$
-algebra by
 ${\hbar } \mu ({\mathfrak {t}}_{\scriptscriptstyle {+}})$
and has basis
${\hbar } \mu ({\mathfrak {t}}_{\scriptscriptstyle {+}})$
and has basis
 $B({\hbar } {G})$
.
$B({\hbar } {G})$
. -
(4) The composition
 $\dot {\mathsf {q}}:=\mathsf {q}\circ \dot {\unicode{x3bd} }_{ {G}}$
is an epimorphism of
$\dot {\mathsf {q}}:=\mathsf {q}\circ \dot {\unicode{x3bd} }_{ {G}}$
is an epimorphism of
 $\mathbb {N}$
-graded algebras which descends to an isomorphism
$\mathbb {N}$
-graded algebras which descends to an isomorphism 
Proof of (2) and (3)
These statements are a minor modification of the statement of Theorem A.7 of [Reference Finkelberg and Tsymbaliuk13]. For the sake of completeness, let us recall the main ingredients, beginning with the proof that
![]() ${\hbar } {G}$
(and thus
${\hbar } {G}$
(and thus
![]() ${\hbar } \mu ({\mathfrak {t}}_{\scriptscriptstyle {+}})$
) is contained in
${\hbar } \mu ({\mathfrak {t}}_{\scriptscriptstyle {+}})$
) is contained in
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
, given in Lemmas A.5 and A.6 of [Reference Finkelberg and Tsymbaliuk13].
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
, given in Lemmas A.5 and A.6 of [Reference Finkelberg and Tsymbaliuk13].
For each
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $x\in \mathfrak {g}$
, and
$x\in \mathfrak {g}$
, and
![]() $i\in \mathbf {I}$
, the formulas of Proposition 3.2 imply that
$i\in \mathbf {I}$
, the formulas of Proposition 3.2 imply that
 $$ \begin{align*} \Delta^n(x)=\sum_{a=1}^n x^{(a)} \quad \text{ and }\quad \Delta^n(t_{i1})=\sum_{a=1}^n t_{i1}^{(a)}+{\hbar}\sum_{ a<b}\mathsf{r}_i^{ab}, \end{align*} $$
$$ \begin{align*} \Delta^n(x)=\sum_{a=1}^n x^{(a)} \quad \text{ and }\quad \Delta^n(t_{i1})=\sum_{a=1}^n t_{i1}^{(a)}+{\hbar}\sum_{ a<b}\mathsf{r}_i^{ab}, \end{align*} $$
where
![]() $y^{(b)}=1^{\otimes (b-1)}\otimes y \otimes 1 ^{\otimes (n-b)}\in Y_{\hbar }(\mathfrak {g})^{\otimes n}$
for any
$y^{(b)}=1^{\otimes (b-1)}\otimes y \otimes 1 ^{\otimes (n-b)}\in Y_{\hbar }(\mathfrak {g})^{\otimes n}$
for any
![]() $y\in Y_{\hbar }(\mathfrak {g})$
and, for each
$y\in Y_{\hbar }(\mathfrak {g})$
and, for each
![]() $a<b$
,
$a<b$
,
![]() $B\mapsto B^{ab}$
is the algebra homomorphism
$B\mapsto B^{ab}$
is the algebra homomorphism
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes 2}\to Y_{\hbar }(\mathfrak {g})^{\otimes n}$
given on simple tensors by
$Y_{\hbar }(\mathfrak {g})^{\otimes 2}\to Y_{\hbar }(\mathfrak {g})^{\otimes n}$
given on simple tensors by
![]() $(x\otimes y)^{ab}=x^{(a)}y^{(b)}$
. Since
$(x\otimes y)^{ab}=x^{(a)}y^{(b)}$
. Since
![]() $(\mathbf {1}-\varepsilon )$
projects
$(\mathbf {1}-\varepsilon )$
projects
![]() $Y_{\hbar }(\mathfrak {g})$
onto
$Y_{\hbar }(\mathfrak {g})$
onto
![]() $\mathrm {Ker}(\varepsilon )$
, it follows readily from these formulas that
$\mathrm {Ker}(\varepsilon )$
, it follows readily from these formulas that
We may now deduce that
![]() ${\hbar } {G}\subset {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
as follows. By (5.1) and the above,
${\hbar } {G}\subset {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
as follows. By (5.1) and the above,
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is a
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is a
![]() $\mathfrak {g}$
-submodule of
$\mathfrak {g}$
-submodule of
![]() $Y_{\hbar }(\mathfrak {g})$
which is preserved by the operators
$Y_{\hbar }(\mathfrak {g})$
which is preserved by the operators
![]() $\{\mathrm {ad}(t_{i1})\}_{i\in \mathbf {I}}$
. Hence, the elements
$\{\mathrm {ad}(t_{i1})\}_{i\in \mathbf {I}}$
. Hence, the elements
necessarily belong to
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
for each
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
for each
![]() $i\in \mathbf {I}$
and
$i\in \mathbf {I}$
and
![]() $k\in \mathbb {N}$
, where
$k\in \mathbb {N}$
, where
![]() $\mathrm {T}_i=(2d_i)^{-1}t_{i1}$
. As
$\mathrm {T}_i=(2d_i)^{-1}t_{i1}$
. As
![]() ${\hbar } x_{\alpha ,k}^\pm $
belongs to the
${\hbar } x_{\alpha ,k}^\pm $
belongs to the
![]() $\mathfrak {g}$
-submodule of
$\mathfrak {g}$
-submodule of
![]() $Y_{\hbar }(\mathfrak {g})$
generated by
$Y_{\hbar }(\mathfrak {g})$
generated by
![]() ${\hbar } x_{ik}^\pm $
, we can conclude that
${\hbar } x_{ik}^\pm $
, we can conclude that
![]() ${\hbar } {G}\subset {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
.
${\hbar } {G}\subset {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
.
Since
![]() $\mathsf {R}_{\hbar }(U({\mathfrak {t}}_{\scriptscriptstyle {+}}))$
has basis given by the set of ordered monomials in
$\mathsf {R}_{\hbar }(U({\mathfrak {t}}_{\scriptscriptstyle {+}}))$
has basis given by the set of ordered monomials in
![]() ${\hbar } q( {G})$
, to complete the proof of both Parts (2) and (3), it suffices to see that
${\hbar } q( {G})$
, to complete the proof of both Parts (2) and (3), it suffices to see that
![]() $B({\hbar } {G})$
spans
$B({\hbar } {G})$
spans
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
. This follows from the fact that
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
. This follows from the fact that
![]() $B( {G})$
is a basis of
$B( {G})$
is a basis of
![]() $Y_{\hbar }(\mathfrak {g})$
together with the crucial Lemma 3.3 of [Reference Gavarini19] (see also [Reference Etingof and Kazhdan11, Lemma 4.12]). We refer the reader to the proof of [Reference Finkelberg and Tsymbaliuk13, Proposition A.2] for complete details.
$Y_{\hbar }(\mathfrak {g})$
together with the crucial Lemma 3.3 of [Reference Gavarini19] (see also [Reference Etingof and Kazhdan11, Lemma 4.12]). We refer the reader to the proof of [Reference Finkelberg and Tsymbaliuk13, Proposition A.2] for complete details.
Proof of (1)
We have already seen that
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is an
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is an
![]() $\mathbb {N}$
-graded subalgebra of
$\mathbb {N}$
-graded subalgebra of
![]() $Y_{\hbar }(\mathfrak {g})$
. That it is a Hopf subalgebra of
$Y_{\hbar }(\mathfrak {g})$
. That it is a Hopf subalgebra of
![]() $Y_{\hbar }(\mathfrak {g})$
is a special case of Proposition 3.3 of [Reference Gavarini20], which passes to completions and makes use of a modification of a technical result for quantized formal series Hopf algebras established in [Reference Enriquez and Halbout9, Proposition 2.1]. It is worth pointing out that, in our specialized setting, it is possible to give a concise direct proof that
$Y_{\hbar }(\mathfrak {g})$
is a special case of Proposition 3.3 of [Reference Gavarini20], which passes to completions and makes use of a modification of a technical result for quantized formal series Hopf algebras established in [Reference Enriquez and Halbout9, Proposition 2.1]. It is worth pointing out that, in our specialized setting, it is possible to give a concise direct proof that
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is a subcoalgebra of
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is a subcoalgebra of
![]() $Y_{\hbar }(\mathfrak {g})$
stable under the antipode S.
$Y_{\hbar }(\mathfrak {g})$
stable under the antipode S.
Indeed, by Proposition 3.2, one has
![]() $\Delta ({\hbar } x)\in {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})^{\otimes 2}$
for
$\Delta ({\hbar } x)\in {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})^{\otimes 2}$
for
![]() $x\in {\hbar } \mathfrak {g}\cup \{t_{i1}\}_{i\in \mathbf {I}}$
. As
$x\in {\hbar } \mathfrak {g}\cup \{t_{i1}\}_{i\in \mathbf {I}}$
. As
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})^{\otimes 2}$
is a
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})^{\otimes 2}$
is a
![]() $\mathfrak {g}$
-submodule of
$\mathfrak {g}$
-submodule of
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes 2}$
stable under all operators
$Y_{\hbar }(\mathfrak {g})^{\otimes 2}$
stable under all operators
![]() $\mathrm {ad}(t_{i1}\otimes 1 + 1\otimes t_{i1})$
, the inclusion
$\mathrm {ad}(t_{i1}\otimes 1 + 1\otimes t_{i1})$
, the inclusion
![]() $\Delta ({\hbar } {G})\subset {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})^{\otimes 2}$
will hold provided
$\Delta ({\hbar } {G})\subset {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})^{\otimes 2}$
will hold provided
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})^{\otimes 2}$
is preserved by the operators
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})^{\otimes 2}$
is preserved by the operators
![]() $\mathrm {ad}({\hbar } \mathsf {r}_i)$
. This is itself a consequence of the fact that
$\mathrm {ad}({\hbar } \mathsf {r}_i)$
. This is itself a consequence of the fact that
![]() $\mathsf {r}_i\in \mathfrak {g}\otimes \mathfrak {g}$
, the inclusion
$\mathsf {r}_i\in \mathfrak {g}\otimes \mathfrak {g}$
, the inclusion
![]() ${\hbar }\mathfrak {g} \subset {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
, that
${\hbar }\mathfrak {g} \subset {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
, that
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})^{\otimes 2}$
is a
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})^{\otimes 2}$
is a
![]() $\mathfrak {g}$
-submodule of
$\mathfrak {g}$
-submodule of
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes 2}$
, and the relation
$Y_{\hbar }(\mathfrak {g})^{\otimes 2}$
, and the relation
Hence, by Part (3), we can conclude that
![]() $\Delta ({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}))\subset {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})^{\otimes 2}$
. A similar argument, using the formulas of Proposition 3.2 and that
$\Delta ({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}))\subset {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})^{\otimes 2}$
. A similar argument, using the formulas of Proposition 3.2 and that
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is a
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is a
![]() $\mathfrak {g}$
-submodule of
$\mathfrak {g}$
-submodule of
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
stable under the operators
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
stable under the operators
![]() $\mathrm {ad}(S(t_{i1}))$
, implies that
$\mathrm {ad}(S(t_{i1}))$
, implies that
![]() $S({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}))\subset {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
.
$S({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}))\subset {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
.
Proof of (4)
By Part (2),
![]() $\dot {\mathsf {q}}$
is an
$\dot {\mathsf {q}}$
is an
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-linear epimorphism with kernel
$\mathbb {C}[{\hbar }]$
-linear epimorphism with kernel
![]() ${\hbar } {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
, and thus gives rise to an isomorphism of graded vector spaces
${\hbar } {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
, and thus gives rise to an isomorphism of graded vector spaces ![]() . To conclude, it suffices to prove that
. To conclude, it suffices to prove that
![]() $\ddot {\mathsf {q}}$
is an algebra homomorphism. By (5.1),
$\ddot {\mathsf {q}}$
is an algebra homomorphism. By (5.1),
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})/{\hbar } {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is commutative, and so the linear map
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})/{\hbar } {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is commutative, and so the linear map
![]() ${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}\to {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})/{\hbar } {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
sending any
${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}\to {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})/{\hbar } {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
sending any
![]() ${\hbar } x\in {\hbar } {\mathfrak {t}}_{\scriptscriptstyle {+}}$
to the image of
${\hbar } x\in {\hbar } {\mathfrak {t}}_{\scriptscriptstyle {+}}$
to the image of
![]() ${\hbar }\mu (x)$
in
${\hbar }\mu (x)$
in
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})/{\hbar } {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
uniquely extends to an algebra homomorphism
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})/{\hbar } {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
uniquely extends to an algebra homomorphism
![]() $\mathsf {p}:\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})\to {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})/{\hbar } {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
. Since
$\mathsf {p}:\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})\to {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})/{\hbar } {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
. Since
![]() $\ddot {\mathsf {q}}\circ \mathsf {p}=\mathbf {1}$
, we can conclude that
$\ddot {\mathsf {q}}\circ \mathsf {p}=\mathbf {1}$
, we can conclude that
![]() $\mathsf {q}$
is the inverse of
$\mathsf {q}$
is the inverse of
![]() $\mathsf {p}$
, and thus an algebra homomorphism.
$\mathsf {p}$
, and thus an algebra homomorphism.
Recall from (3.14) that
![]() $Y_{\hbar }\mathfrak {g}$
denotes the
$Y_{\hbar }\mathfrak {g}$
denotes the
![]() ${\hbar }$
-adically complete Yangian associated with
${\hbar }$
-adically complete Yangian associated with
![]() $\mathfrak {g}$
, and let
$\mathfrak {g}$
, and let
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
denote the
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
denote the
![]() ${\hbar }$
-adic completion of the Hopf algebra
${\hbar }$
-adic completion of the Hopf algebra
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
:
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
:
As an immediate consequence of the above proposition and Corollary 2.6, we obtain the following result.
Corollary 5.3
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
is a topologically free,
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
is a topologically free,
![]() $\mathbb {N}$
-graded topological Hopf algebra over
$\mathbb {N}$
-graded topological Hopf algebra over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
of finite type. Moreover:
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
of finite type. Moreover:
-
(1)
 ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
is a flat deformation of the
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
is a flat deformation of the
 $\mathbb {N}$
-graded algebra
$\mathbb {N}$
-graded algebra
 $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
over
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
over
 $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. In particular,
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. In particular,
 ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\cong \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as an
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\cong \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as an
 $\mathbb {N}$
-graded topological
$\mathbb {N}$
-graded topological
 $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module. -
(2)
 ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
is a topological Hopf subalgebra of the completed Yangian
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
is a topological Hopf subalgebra of the completed Yangian
 $Y_{\hbar }\mathfrak {g}$
.
$Y_{\hbar }\mathfrak {g}$
.
The statement that
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
is of finite type reduces to the fact that the homogeneous components
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
is of finite type reduces to the fact that the homogeneous components
![]() $\mathsf {S}_{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
of
$\mathsf {S}_{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
of
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
are all finite-dimensional complex vector spaces (see below Corollary 2.9).
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
are all finite-dimensional complex vector spaces (see below Corollary 2.9).
Henceforth, we will identify
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
with the semiclassical limit of
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
with the semiclassical limit of
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
as an
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
as an
![]() $\mathbb {N}$
-graded Hopf algebra. We emphasize that this is a non-cocommutative Hopf algebra; in particular, it is not isomorphic to the standard symmetric Hopf algebra on
$\mathbb {N}$
-graded Hopf algebra. We emphasize that this is a non-cocommutative Hopf algebra; in particular, it is not isomorphic to the standard symmetric Hopf algebra on
![]() ${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}$
, which we denote by
${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}$
, which we denote by
![]() $\mathbb {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
. However,
$\mathbb {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
. However,
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
and
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
and
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
are filtered deformations of
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
are filtered deformations of
![]() $\mathsf {R}_{\hbar }( U({\mathfrak {t}}_{\scriptscriptstyle {+}}))$
and
$\mathsf {R}_{\hbar }( U({\mathfrak {t}}_{\scriptscriptstyle {+}}))$
and
![]() $\mathbb {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
, respectively, as we now explain. Consider the Hopf ideal
$\mathbb {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
, respectively, as we now explain. Consider the Hopf ideal
Here, we note that it follows from Part (3) of the above proposition that, for each pair of positive integers
![]() $k,n\in \mathbb {N}_+$
, one has
$k,n\in \mathbb {N}_+$
, one has
In particular,
![]() $\mathbf {J}^k={\hbar }^k Y_{\hbar }(\mathfrak {g}) \cap {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
for each
$\mathbf {J}^k={\hbar }^k Y_{\hbar }(\mathfrak {g}) \cap {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
for each
![]() $k\in \mathbb {N}$
, and so the associated graded Hopf algebra
$k\in \mathbb {N}$
, and so the associated graded Hopf algebra
![]() ${\mathrm {gr}}_{\mathbf {J}}({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}))$
with respect to the
${\mathrm {gr}}_{\mathbf {J}}({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}))$
with respect to the
![]() $\mathbf {J}$
-adic filtration embeds inside the associated graded Hopf algebra
$\mathbf {J}$
-adic filtration embeds inside the associated graded Hopf algebra
![]() ${\mathrm {gr}}_{\hbar }(Y_{\hbar }(\mathfrak {g}))$
of
${\mathrm {gr}}_{\hbar }(Y_{\hbar }(\mathfrak {g}))$
of
![]() $Y_{\hbar }(\mathfrak {g})$
with respect to the
$Y_{\hbar }(\mathfrak {g})$
with respect to the
![]() ${\hbar }$
-adic filtration. Since
${\hbar }$
-adic filtration. Since
![]() $Y_{\hbar }(\mathfrak {g})$
is a torsion-free Hopf algebra deformation of
$Y_{\hbar }(\mathfrak {g})$
is a torsion-free Hopf algebra deformation of
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
over
$U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
over
![]() $\mathbb {C}[{\hbar }]$
, we have isomorphisms of graded Hopf algebras
$\mathbb {C}[{\hbar }]$
, we have isomorphisms of graded Hopf algebras
 $$ \begin{gather*} {\mathrm{gr}}_{\hbar}(Y_{\hbar}(\mathfrak{g}))=\bigoplus_{n\in \mathbb{N}} {\hbar}^n Y_{\hbar}(\mathfrak{g})/{\hbar}^{n+1}Y_{\hbar}(\mathfrak{g}) \cong \bigoplus_{n\in \mathbb{N}}{\hbar}^n U({\mathfrak{t}}_{\scriptscriptstyle{+}})=U({\mathfrak{t}}_{\scriptscriptstyle{+}})[{\hbar}], \\ {\mathrm{gr}}_{\mathbf{J}}({\dot{\mathsf{Y}}}_{\hbar}(\mathfrak{g}))=\bigoplus_{n\in \mathbb{N}} \mathbf{J}^n/\mathbf{J}^{n+1}\cong \bigoplus_{n\in \mathbb{N}}{\hbar}^n {\mathbf{F}}_n(U({\mathfrak{t}}_{\scriptscriptstyle{+}}))=\mathsf{R}_{\hbar}( U({\mathfrak{t}}_{\scriptscriptstyle{+}})), \end{gather*} $$
$$ \begin{gather*} {\mathrm{gr}}_{\hbar}(Y_{\hbar}(\mathfrak{g}))=\bigoplus_{n\in \mathbb{N}} {\hbar}^n Y_{\hbar}(\mathfrak{g})/{\hbar}^{n+1}Y_{\hbar}(\mathfrak{g}) \cong \bigoplus_{n\in \mathbb{N}}{\hbar}^n U({\mathfrak{t}}_{\scriptscriptstyle{+}})=U({\mathfrak{t}}_{\scriptscriptstyle{+}})[{\hbar}], \\ {\mathrm{gr}}_{\mathbf{J}}({\dot{\mathsf{Y}}}_{\hbar}(\mathfrak{g}))=\bigoplus_{n\in \mathbb{N}} \mathbf{J}^n/\mathbf{J}^{n+1}\cong \bigoplus_{n\in \mathbb{N}}{\hbar}^n {\mathbf{F}}_n(U({\mathfrak{t}}_{\scriptscriptstyle{+}}))=\mathsf{R}_{\hbar}( U({\mathfrak{t}}_{\scriptscriptstyle{+}})), \end{gather*} $$
where the second isomorphism follows from the first and Proposition 5.2. In fact, the module isomorphisms
![]() $\unicode{x3bd} _{ {G}}$
and
$\unicode{x3bd} _{ {G}}$
and
![]() $\dot {\unicode{x3bd} }_{ {G}}$
are filtered, and the above identifications can be realized as the associated graded maps
$\dot {\unicode{x3bd} }_{ {G}}$
are filtered, and the above identifications can be realized as the associated graded maps
![]() $\mathrm {gr}(\unicode{x3bd} _{ {G}})$
and
$\mathrm {gr}(\unicode{x3bd} _{ {G}})$
and
![]() $\mathrm {gr}(\dot {\unicode{x3bd} }_{ {G}})$
, respectively.
$\mathrm {gr}(\dot {\unicode{x3bd} }_{ {G}})$
, respectively.
The image of
![]() $\mathbf {J}$
under the quotient map
$\mathbf {J}$
under the quotient map
![]() $\dot {\mathsf {q}}$
is the Hopf ideal
$\dot {\mathsf {q}}$
is the Hopf ideal
where
![]() $\mathsf {S}^{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
denotes the nth symmetric power of
$\mathsf {S}^{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
denotes the nth symmetric power of
![]() ${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}$
. This is also a Hopf ideal in
${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}$
. This is also a Hopf ideal in
![]() $\mathbb {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
, and one has a canonical isomorphism
$\mathbb {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
, and one has a canonical isomorphism
![]() ${\mathrm {gr}}_{\mathbb {J}}\mathbb {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})\cong \mathbb {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
of graded Hopf algebras. Since the elements of
${\mathrm {gr}}_{\mathbb {J}}\mathbb {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})\cong \mathbb {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
of graded Hopf algebras. Since the elements of
![]() $\mu ({\mathfrak {t}}_{\scriptscriptstyle {+}})$
are primitive modulo
$\mu ({\mathfrak {t}}_{\scriptscriptstyle {+}})$
are primitive modulo
![]() ${\hbar } Y_{\hbar }(\mathfrak {g})^{\otimes 2}$
, the subspace
${\hbar } Y_{\hbar }(\mathfrak {g})^{\otimes 2}$
, the subspace
![]() ${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}=\mathbb {J}/\mathbb {J}^2$
of
${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}=\mathbb {J}/\mathbb {J}^2$
of
![]() ${\mathrm {gr}}_{\mathbb {J}}\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
consists of primitive elements, and we can conclude that
${\mathrm {gr}}_{\mathbb {J}}\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
consists of primitive elements, and we can conclude that
as graded Hopf algebras.
Remark 5.4 Since
![]() $\mathbf {J}^k={\hbar }^k Y_{\hbar }(\mathfrak {g})\cap {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
for each
$\mathbf {J}^k={\hbar }^k Y_{\hbar }(\mathfrak {g})\cap {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
for each
![]() $k\in \mathbb {N}$
, the closure of
$k\in \mathbb {N}$
, the closure of
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
in the quantized enveloping algebra
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
in the quantized enveloping algebra
![]() $Y_{\hbar }\mathfrak {g}$
coincides with the
$Y_{\hbar }\mathfrak {g}$
coincides with the
![]() $\mathbf {J}$
-adic completion
$\mathbf {J}$
-adic completion
This is precisely the quantized formal series Hopf algebra
![]() $U_{\hbar }{\mathfrak {b}}^\prime $
from Section 5.1 associated with
$U_{\hbar }{\mathfrak {b}}^\prime $
from Section 5.1 associated with
![]() $U_{\hbar }\mathfrak {b}=Y_{\hbar }\mathfrak {g}$
. As
$U_{\hbar }\mathfrak {b}=Y_{\hbar }\mathfrak {g}$
. As
![]() $\mathbf {J}$
surjects onto the ideal
$\mathbf {J}$
surjects onto the ideal
![]() $\mathbb {J}$
from (5.4), the quotient map
$\mathbb {J}$
from (5.4), the quotient map
![]() $\dot {\mathsf {q}}$
induces an isomorphism of
$\dot {\mathsf {q}}$
induces an isomorphism of
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras
5.3 Triangular decomposition
Proposition 5.2 implies that the triangular decomposition of
![]() $Y_{\hbar }(\mathfrak {g})$
, reviewed in Section 3.4, induces a triangular decomposition on
$Y_{\hbar }(\mathfrak {g})$
, reviewed in Section 3.4, induces a triangular decomposition on
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
, with the
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
, with the
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-algebras
$\mathbb {C}[{\hbar }]$
-algebras
playing the roles of
![]() $Y_{\hbar }^\pm (\mathfrak {g})$
and
$Y_{\hbar }^\pm (\mathfrak {g})$
and
![]() $Y_{\hbar }^0(\mathfrak {g})$
, respectively. In this subsection, we spell this out explicitly. Let us set
$Y_{\hbar }^0(\mathfrak {g})$
, respectively. In this subsection, we spell this out explicitly. Let us set
and recall from Section 3.4 that
![]() $\unicode{x3bd} _\pm $
and
$\unicode{x3bd} _\pm $
and
![]() $\unicode{x3be} $
are the isomorphisms
$\unicode{x3be} $
are the isomorphisms
defined above (3.13) and in the statement of Proposition 3.5, respectively. We further recall from (3.17) that, for each
![]() $\beta \in Q_+$
,
$\beta \in Q_+$
,
![]() $\nu (\beta )\in \mathbb {N}$
is defined by
$\nu (\beta )\in \mathbb {N}$
is defined by
The following corollary provides an analogue of Proposition 5.2 for the subalgebras
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})$
and
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})$
and
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{0}(\mathfrak {g})$
.
${\dot {\mathsf {Y}}}_{\hbar }^{0}(\mathfrak {g})$
.
Corollary 5.5 Let ![]() and
and
![]() denote the restrictions of
denote the restrictions of
![]() $\unicode{x3bd} _\pm $
and
$\unicode{x3bd} _\pm $
and
![]() $\unicode{x3be} $
to
$\unicode{x3be} $
to
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})$
and
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})$
and
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{0}(\mathfrak {g})$
, respectively. Then:
${\dot {\mathsf {Y}}}_{\hbar }^{0}(\mathfrak {g})$
, respectively. Then:
-
(1)
 is an isomorphism of
is an isomorphism of
 $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
 $\mathbb {C}[{\hbar }]$
-modules
$\mathbb {C}[{\hbar }]$
-modules 
-
(2)
 is an isomorphism of
is an isomorphism of
 $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
 $\mathbb {C}[{\hbar }]$
-algebras
$\mathbb {C}[{\hbar }]$
-algebras 
-
(3)
 ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})$
is a torsion-free,
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})$
is a torsion-free,
 $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
 $\mathbb {C}[{\hbar }]$
-algebra deformation of
$\mathbb {C}[{\hbar }]$
-algebra deformation of
 $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}^\pm )$
. In particular, there is an isomorphism of graded
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}^\pm )$
. In particular, there is an isomorphism of graded
 $\mathbb {C}[{\hbar }]$
-modules
$\mathbb {C}[{\hbar }]$
-modules  $$ \begin{align*} {\dot{\mathsf{Y}}}_{\hbar}^{\pm}(\mathfrak{g})\cong \mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}^\pm)[{\hbar}]. \end{align*} $$
$$ \begin{align*} {\dot{\mathsf{Y}}}_{\hbar}^{\pm}(\mathfrak{g})\cong \mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}^\pm)[{\hbar}]. \end{align*} $$
-
(4)
 ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})$
is a Q-graded subalgebra of
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})$
is a Q-graded subalgebra of
 ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})$
with
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})$
with  $$ \begin{align*} {\dot{\mathsf{Y}}}_{\hbar}^{\pm}(\mathfrak{g})_{\pm \beta} \subset \mathbf{J}^{\nu(\beta)}\subset {\hbar}^{\nu(\beta)}Y_{\hbar}^\pm(\mathfrak{g})_{\pm \beta} \quad \forall \; \beta \in Q_+. \end{align*} $$
$$ \begin{align*} {\dot{\mathsf{Y}}}_{\hbar}^{\pm}(\mathfrak{g})_{\pm \beta} \subset \mathbf{J}^{\nu(\beta)}\subset {\hbar}^{\nu(\beta)}Y_{\hbar}^\pm(\mathfrak{g})_{\pm \beta} \quad \forall \; \beta \in Q_+. \end{align*} $$
We note that each of these results follows readily from Propositions 3.5 and 5.2, in addition to Corollary 2.6 in the case of Part (3). We leave the details as an exercise to the interested reader. As a consequence of this corollary and Proposition 5.2, we obtain the following analogue of Part (3) from Proposition 3.5.
Corollary 5.6 The multiplication map
is an isomorphism of
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-modules.
$\mathbb {C}[{\hbar }]$
-modules.
Remark 5.7 As in Remark 3.7, the above results can easily be lifted to the
![]() ${\hbar }$
-adic setting using Corollary 2.6 (see also Corollary 5.3). We especially note that, for each choice of the symbol
${\hbar }$
-adic setting using Corollary 2.6 (see also Corollary 5.3). We especially note that, for each choice of the symbol
![]() $\chi $
, the
$\chi $
, the
![]() ${\hbar }$
-adic completion
${\hbar }$
-adic completion
is a topologically free
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra of finite type, which provides a flat deformation of the symmetric algebra
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra of finite type, which provides a flat deformation of the symmetric algebra
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}^\chi )$
over
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}^\chi )$
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. In addition,
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. In addition,
![]() ${\dot {\mathsf {Y}}}_{\hbar }^\chi \mathfrak {g}$
embeds inside the completed Yangian
${\dot {\mathsf {Y}}}_{\hbar }^\chi \mathfrak {g}$
embeds inside the completed Yangian
![]() $Y_{\hbar }\mathfrak {g}$
, and the multiplication map induces an isomorphism of
$Y_{\hbar }\mathfrak {g}$
, and the multiplication map induces an isomorphism of
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
where
![]() $\otimes $
is now the topological tensor product
$\otimes $
is now the topological tensor product
![]() $\widehat {\otimes }$
over
$\widehat {\otimes }$
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
(see Remark 2.11).
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
(see Remark 2.11).
5.4 The adjoint and coadjoint actions
We now prove two lemmas concerning the Drinfeld–Gavarini subalgebra
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
which will play an important role in the main results and constructions of Sections 7 and 8. The first of these, Lemma 5.8, will be used to construct the quantum double of the Yangian in Section 8.2.
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
which will play an important role in the main results and constructions of Sections 7 and 8. The first of these, Lemma 5.8, will be used to construct the quantum double of the Yangian in Section 8.2.
Let
![]() $\blacktriangledown :Y_{\hbar }(\mathfrak {g})\otimes Y_{\hbar }(\mathfrak {g})\to Y_{\hbar }(\mathfrak {g})$
and
$\blacktriangledown :Y_{\hbar }(\mathfrak {g})\otimes Y_{\hbar }(\mathfrak {g})\to Y_{\hbar }(\mathfrak {g})$
and
![]() $\blacktriangle :Y_{\hbar }(\mathfrak {g})\to Y_{\hbar }(\mathfrak {g})\otimes Y_{\hbar }(\mathfrak {g})$
denote the left adjoint action of
$\blacktriangle :Y_{\hbar }(\mathfrak {g})\to Y_{\hbar }(\mathfrak {g})\otimes Y_{\hbar }(\mathfrak {g})$
denote the left adjoint action of
![]() $Y_{\hbar }(\mathfrak {g})$
on itself, and the right adjoint coaction of
$Y_{\hbar }(\mathfrak {g})$
on itself, and the right adjoint coaction of
![]() $Y_{\hbar }(\mathfrak {g})$
on itself, respectively. That is,
$Y_{\hbar }(\mathfrak {g})$
on itself, respectively. That is,
 $$ \begin{gather*} \blacktriangledown= m^3\circ (\mathbf{1}^{\otimes 2}\otimes S)\circ (2\,3)\circ (\Delta \otimes \mathbf{1}), \\ \blacktriangle=(1\otimes m)\circ (1\,2)\circ (S\otimes \mathbf{1}^{\otimes 2})\circ \Delta^3. \end{gather*} $$
$$ \begin{gather*} \blacktriangledown= m^3\circ (\mathbf{1}^{\otimes 2}\otimes S)\circ (2\,3)\circ (\Delta \otimes \mathbf{1}), \\ \blacktriangle=(1\otimes m)\circ (1\,2)\circ (S\otimes \mathbf{1}^{\otimes 2})\circ \Delta^3. \end{gather*} $$
The
![]() ${\hbar }$
-adic analogue of the below result, for a quantized enveloping algebra
${\hbar }$
-adic analogue of the below result, for a quantized enveloping algebra
![]() $U_{\hbar }\mathfrak {b}$
with
$U_{\hbar }\mathfrak {b}$
with
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
replaced by
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
replaced by
![]() $U_{\hbar }{\mathfrak {b}}^\prime $
, was established in Propositions 4.3 and 4.4 of [Reference Appel and Toledano Laredo1] (see also Proposition A.5 therein).
$U_{\hbar }{\mathfrak {b}}^\prime $
, was established in Propositions 4.3 and 4.4 of [Reference Appel and Toledano Laredo1] (see also Proposition A.5 therein).
Lemma 5.8 One has
Proof Since
![]() $\blacktriangledown $
makes
$\blacktriangledown $
makes
![]() $Y_{\hbar }(\mathfrak {g})$
a left module, to prove the first inclusion, it suffices to show that
$Y_{\hbar }(\mathfrak {g})$
a left module, to prove the first inclusion, it suffices to show that
![]() $x\cdot y:=\blacktriangledown (x\otimes y)\in {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
for all
$x\cdot y:=\blacktriangledown (x\otimes y)\in {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
for all
![]() $x\in \mathfrak {g}\cup \{t_{i1}\}_{i\in \mathbf {I}}$
and
$x\in \mathfrak {g}\cup \{t_{i1}\}_{i\in \mathbf {I}}$
and
![]() $y\in {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
. Since
$y\in {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
. Since
this follows from the observation that
![]() ${\hbar } \mathsf {r}_i\in \mathfrak {g}\otimes {\hbar }\mathfrak {g}\subset \mathfrak {g}\otimes {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
and the fact that
${\hbar } \mathsf {r}_i\in \mathfrak {g}\otimes {\hbar }\mathfrak {g}\subset \mathfrak {g}\otimes {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
and the fact that
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is a
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is a
![]() $\mathfrak {g}$
-submodule of
$\mathfrak {g}$
-submodule of
![]() $Y_{\hbar }(\mathfrak {g})$
stable under
$Y_{\hbar }(\mathfrak {g})$
stable under
![]() $\mathrm {ad}(t_{i1})$
for all
$\mathrm {ad}(t_{i1})$
for all
![]() $i\in \mathbf {I}$
.
$i\in \mathbf {I}$
.
As for the second inclusion, note that
![]() $\blacktriangle $
is a homomorphism of right modules:
$\blacktriangle $
is a homomorphism of right modules:
where
![]() $\gamma :Y_{\hbar }(\mathfrak {g})^{\otimes 2}\otimes Y_{\hbar }(\mathfrak {g})\to Y_{\hbar }(\mathfrak {g})^{\otimes 2}$
is the right action defined by
$\gamma :Y_{\hbar }(\mathfrak {g})^{\otimes 2}\otimes Y_{\hbar }(\mathfrak {g})\to Y_{\hbar }(\mathfrak {g})^{\otimes 2}$
is the right action defined by
This right action preserves
![]() $Y_{\hbar }(\mathfrak {g})\otimes {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\subset Y_{\hbar }(\mathfrak {g})^{\otimes 2}$
. Indeed, if
$Y_{\hbar }(\mathfrak {g})\otimes {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\subset Y_{\hbar }(\mathfrak {g})^{\otimes 2}$
. Indeed, if
![]() $y\in Y_{\hbar }(\mathfrak {g})$
,
$y\in Y_{\hbar }(\mathfrak {g})$
,
![]() $z\in {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
, and
$z\in {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
, and
![]() $x\in \mathfrak {g}$
, we have
$x\in \mathfrak {g}$
, we have
and replacing x by
![]() $t_{i1}$
, for any
$t_{i1}$
, for any
![]() $i\in \mathbf {I}$
, yields instead
$i\in \mathbf {I}$
, yields instead
which again belongs to
![]() $Y_{\hbar }(\mathfrak {g})\otimes {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
as
$Y_{\hbar }(\mathfrak {g})\otimes {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
as
![]() ${\hbar } \mathsf {r}_i^{21}, {\hbar } \mathsf {r}_i\in ({\hbar }\mathfrak {g}\otimes \mathfrak {g})\cap (\mathfrak {g}\otimes {\hbar }\mathfrak {g})$
and
${\hbar } \mathsf {r}_i^{21}, {\hbar } \mathsf {r}_i\in ({\hbar }\mathfrak {g}\otimes \mathfrak {g})\cap (\mathfrak {g}\otimes {\hbar }\mathfrak {g})$
and
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is an
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is an
![]() $\mathrm {ad}(t_{i1})$
-stable
$\mathrm {ad}(t_{i1})$
-stable
![]() $\mathfrak {g}$
-submodule of
$\mathfrak {g}$
-submodule of
![]() $Y_{\hbar }(\mathfrak {g})$
.
$Y_{\hbar }(\mathfrak {g})$
.
Since
![]() $Y_{\hbar }(\mathfrak {g})\otimes {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is a right submodule of
$Y_{\hbar }(\mathfrak {g})\otimes {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is a right submodule of
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes 2}$
under
$Y_{\hbar }(\mathfrak {g})^{\otimes 2}$
under
![]() $\gamma $
, the condition (5.5) guarantees that
$\gamma $
, the condition (5.5) guarantees that
![]() $\blacktriangle (Y_{\hbar }(\mathfrak {g}))\subset Y_{\hbar }(\mathfrak {g})\otimes {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
will hold provided it holds on
$\blacktriangle (Y_{\hbar }(\mathfrak {g}))\subset Y_{\hbar }(\mathfrak {g})\otimes {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
will hold provided it holds on
![]() $\mathfrak {g}\cup \{t_{i1}\}_{i\in \mathbf {I}}$
. To conclude, it suffices to note that, for each
$\mathfrak {g}\cup \{t_{i1}\}_{i\in \mathbf {I}}$
. To conclude, it suffices to note that, for each
![]() $x\in \mathfrak {g}$
and
$x\in \mathfrak {g}$
and
![]() $i\in \mathbf {I}$
, one has
$i\in \mathbf {I}$
, one has
 $$ \begin{gather*} \blacktriangle(x)=x\otimes 1\in Y_{\hbar}(\mathfrak{g})\otimes {\dot{\mathsf{Y}}}_{\hbar}(\mathfrak{g}), \\ \blacktriangle(t_{i1})=t_{i1}\otimes 1+{\hbar}(\mathsf{r}_i-\mathsf{r}_i^{21})\in Y_{\hbar}(\mathfrak{g})\otimes {\dot{\mathsf{Y}}}_{\hbar}(\mathfrak{g}).\\[-37pt] \end{gather*} $$
$$ \begin{gather*} \blacktriangle(x)=x\otimes 1\in Y_{\hbar}(\mathfrak{g})\otimes {\dot{\mathsf{Y}}}_{\hbar}(\mathfrak{g}), \\ \blacktriangle(t_{i1})=t_{i1}\otimes 1+{\hbar}(\mathsf{r}_i-\mathsf{r}_i^{21})\in Y_{\hbar}(\mathfrak{g})\otimes {\dot{\mathsf{Y}}}_{\hbar}(\mathfrak{g}).\\[-37pt] \end{gather*} $$
5.5 The R-matrix
The second lemma we will need concerns the universal R-matrix
![]() $\mathcal {R}(z)$
of the Yangian, and will play a crucial role in identifying the dual Yangian as a subalgebra of the Yangian double
$\mathcal {R}(z)$
of the Yangian, and will play a crucial role in identifying the dual Yangian as a subalgebra of the Yangian double
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
in Section 7. In what follows, all notation is as in Section 3.6.
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
in Section 7. In what follows, all notation is as in Section 3.6.
Lemma 5.9 The factors
![]() $\mathcal {R}^\pm (z)$
and
$\mathcal {R}^\pm (z)$
and
![]() $\mathcal {R}^0(z)$
of the universal R-matrix
$\mathcal {R}^0(z)$
of the universal R-matrix
![]() $\mathcal {R}(z)$
have coefficients in
$\mathcal {R}(z)$
have coefficients in
![]() $({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\otimes Y_{\hbar }(\mathfrak {g}))\cap (Y_{\hbar }(\mathfrak {g})\cap {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}))$
. Consequently,
$({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\otimes Y_{\hbar }(\mathfrak {g}))\cap (Y_{\hbar }(\mathfrak {g})\cap {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}))$
. Consequently,
Proof Since
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is preserved by
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is preserved by
![]() $\mathrm {ad}(t_{i1})$
for any
$\mathrm {ad}(t_{i1})$
for any
![]() $i\in \mathbf {I}$
and, for each
$i\in \mathbf {I}$
and, for each
![]() $\alpha \in \Delta ^+$
, the simple tensor
$\alpha \in \Delta ^+$
, the simple tensor
![]() ${\hbar } x_\alpha ^-\otimes x_\alpha ^+=x_\alpha ^-\otimes {\hbar } x_\alpha ^+$
belongs to the intersection of
${\hbar } x_\alpha ^-\otimes x_\alpha ^+=x_\alpha ^-\otimes {\hbar } x_\alpha ^+$
belongs to the intersection of
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\otimes Y_{\hbar }(\mathfrak {g})$
and
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\otimes Y_{\hbar }(\mathfrak {g})$
and
![]() $Y_{\hbar }(\mathfrak {g})\otimes {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
, it follows from (3.18) and induction on
$Y_{\hbar }(\mathfrak {g})\otimes {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
, it follows from (3.18) and induction on
![]() $\mathrm {ht}(\beta )$
that
$\mathrm {ht}(\beta )$
that
Consequently, both
![]() $\mathcal {R}^-(z)$
and
$\mathcal {R}^-(z)$
and
![]() $\mathcal {R}^+(z)=\mathcal {R}^-_{21}(-z)^{-1}$
belong to the intersection of
$\mathcal {R}^+(z)=\mathcal {R}^-_{21}(-z)^{-1}$
belong to the intersection of
![]() $({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\otimes Y_{\hbar }(\mathfrak {g}))[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
and
$({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\otimes Y_{\hbar }(\mathfrak {g}))[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
and
![]() $(Y_{\hbar }(\mathfrak {g})\otimes {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}))[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. It is thus enough to prove that
$(Y_{\hbar }(\mathfrak {g})\otimes {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}))[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. It is thus enough to prove that
Recall from (5.2) that
![]() $\mathbf {J}={\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\cap {\hbar } Y_{\hbar }(\mathfrak {g})$
. Since
$\mathbf {J}={\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\cap {\hbar } Y_{\hbar }(\mathfrak {g})$
. Since
![]() ${\hbar } h_i(u)\in \mathbf {J}[\kern-1.2pt\![u^{-1}]\!\kern-1.2pt]$
, the logarithm
${\hbar } h_i(u)\in \mathbf {J}[\kern-1.2pt\![u^{-1}]\!\kern-1.2pt]$
, the logarithm
![]() $t_i(u)=\log (1+{\hbar } h_i(u))$
and its Borel transform
$t_i(u)=\log (1+{\hbar } h_i(u))$
and its Borel transform
![]() $B_i(u)$
both have coefficients in
$B_i(u)$
both have coefficients in
![]() $\mathbf {J}$
. Therefore, we have
$\mathbf {J}$
. Therefore, we have
Since
![]() $g(z/2\kappa {\hbar })$
is divisible by
$g(z/2\kappa {\hbar })$
is divisible by
![]() ${\hbar }$
, it follows from (3.19) that the logarithm
${\hbar }$
, it follows from (3.19) that the logarithm
![]() $\mathcal {S}(z)$
of
$\mathcal {S}(z)$
of
![]() $\mathcal {R}^0(z)$
, and thus
$\mathcal {R}^0(z)$
, and thus
![]() $\mathcal {R}^0(z)$
itself, has coefficients belonging to the intersection of
$\mathcal {R}^0(z)$
itself, has coefficients belonging to the intersection of
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\otimes Y_{\hbar }(\mathfrak {g})$
and
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\otimes Y_{\hbar }(\mathfrak {g})$
and
![]() $Y_{\hbar }(\mathfrak {g})\otimes {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
.
$Y_{\hbar }(\mathfrak {g})\otimes {\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
.
6 The dual Yangian
With Section 5 at our disposal, we are now in a position to introduce the dual Yangian
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. After defining
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. After defining
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
and spelling out some of its basic properties in Sections 6.1 and 6.2, we prove in Sections 6.3 and 6.4 that it is a homogeneous quantization of the Lie bialgebra
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
and spelling out some of its basic properties in Sections 6.1 and 6.2, we prove in Sections 6.3 and 6.4 that it is a homogeneous quantization of the Lie bialgebra
![]() $({\mathfrak {t}}_{\scriptscriptstyle {-}},\delta _{\scriptscriptstyle {-}})$
defined in Section 2.5. We conclude in Section 6.5 by identifying a family of generators for
$({\mathfrak {t}}_{\scriptscriptstyle {-}},\delta _{\scriptscriptstyle {-}})$
defined in Section 2.5. We conclude in Section 6.5 by identifying a family of generators for
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
and establishing a triangular decomposition.
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
and establishing a triangular decomposition.
6.1 The dual Yangian
 ${{{\dot {\mathsf {Y}}}_{{\hbar }{\mathfrak {g}}}}{\vphantom {)}}^\star }$
${{{\dot {\mathsf {Y}}}_{{\hbar }{\mathfrak {g}}}}{\vphantom {)}}^\star }$
By Corollary 5.3, the
![]() ${\hbar }$
-adic completion
${\hbar }$
-adic completion
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
of
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
of
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is an
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is an
![]() $\mathbb {N}$
-graded topological Hopf algebra of finite type. We may thus apply the machinery from Section 2.3 to obtain a
$\mathbb {N}$
-graded topological Hopf algebra of finite type. We may thus apply the machinery from Section 2.3 to obtain a
![]() $\mathbb {Z}$
-graded topological Hopf structure on its restricted dual.
$\mathbb {Z}$
-graded topological Hopf structure on its restricted dual.
In more detail, by Proposition 2.10, the restricted dual
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
, as defined in Definition 2.7, is a
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
, as defined in Definition 2.7, is a
![]() $\mathbb {Z}$
-graded topological Hopf algebra over
$\mathbb {Z}$
-graded topological Hopf algebra over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
with product, unit, coproduct, counit, and antipode given by the transposes
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
with product, unit, coproduct, counit, and antipode given by the transposes
 $$ \begin{gather*} \Delta^t: {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star \otimes {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star \to {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star, \quad \varepsilon^t: \mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt]\to {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star,\\ m^t:{\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star \to {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star \otimes {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star, \quad \iota^t:{\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star\to\mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt],\quad S^t:{\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star\to {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star, \end{gather*} $$
$$ \begin{gather*} \Delta^t: {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star \otimes {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star \to {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star, \quad \varepsilon^t: \mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt]\to {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star,\\ m^t:{\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star \to {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star \otimes {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star, \quad \iota^t:{\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star\to\mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt],\quad S^t:{\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star\to {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star, \end{gather*} $$
respectively, where
![]() $\Delta $
,
$\Delta $
,
![]() $\varepsilon $
, m,
$\varepsilon $
, m,
![]() $\iota $
, and S are the coproduct, counit, product, unit, and antipode of
$\iota $
, and S are the coproduct, counit, product, unit, and antipode of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
, respectively, and
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
, respectively, and
![]() $\otimes $
is the topological tensor product over
$\otimes $
is the topological tensor product over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
(see Remark 2.11).
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
(see Remark 2.11).
Definition 6.1 The topological Hopf algebra
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
introduced above is called the dual Yangian of
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
introduced above is called the dual Yangian of
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
Explicitly,
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is the subspace of the
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is the subspace of the
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear dual
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear dual
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\ast $
consisting of those
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\ast $
consisting of those
![]() $f:{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\to \mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
which are continuous with respect to the gradation topology on
$f:{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\to \mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
which are continuous with respect to the gradation topology on
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
. It can be recovered as the
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
. It can be recovered as the
![]() ${\hbar }$
-adic completion of the
${\hbar }$
-adic completion of the
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-algebra
$\mathbb {C}[{\hbar }]$
-algebra
where
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}){\vphantom {)}}^\star $
is the graded dual of
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}){\vphantom {)}}^\star $
is the graded dual of
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
over
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
over
![]() $\mathbb {C}[{\hbar }]$
which, as explained in Remark 2.8, coincides with
$\mathbb {C}[{\hbar }]$
which, as explained in Remark 2.8, coincides with
![]() $({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star )_{\mathbb {Z}}$
under the natural identification of
$({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star )_{\mathbb {Z}}$
under the natural identification of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\ast $
with
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\ast $
with
![]() $\mathrm {Hom}_{\mathbb {C}[{\hbar }]}({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}),\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])$
. Here, we have set
$\mathrm {Hom}_{\mathbb {C}[{\hbar }]}({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}),\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])$
. Here, we have set
By Corollary 2.9,
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is a flat deformation of the graded Hopf algebra
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is a flat deformation of the graded Hopf algebra
In particular, the dual Yangian
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is isomorphic to
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is isomorphic to
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star [\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as a
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star [\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as a
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module. Here, we recall that
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module. Here, we recall that
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
is the graded dual of the
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
is the graded dual of the
![]() $\mathbb {N}$
-graded Hopf algebra
$\mathbb {N}$
-graded Hopf algebra
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
over
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
over
![]() $\mathbb {C}$
. As a vector space, one has
$\mathbb {C}$
. As a vector space, one has
where
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star _{-n}=\mathsf {S}_{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\ast \subset \mathrm {Hom}_{\mathbb {C}}(\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}),\mathbb {C})$
. We shall identify this Hopf algebra with the enveloping algebra of the Lie algebra
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star _{-n}=\mathsf {S}_{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\ast \subset \mathrm {Hom}_{\mathbb {C}}(\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}),\mathbb {C})$
. We shall identify this Hopf algebra with the enveloping algebra of the Lie algebra
![]() ${\mathfrak {t}}_{\scriptscriptstyle {-}}=t^{-1}\mathfrak {g}[t^{-1}]$
in Section 6.3 below.
${\mathfrak {t}}_{\scriptscriptstyle {-}}=t^{-1}\mathfrak {g}[t^{-1}]$
in Section 6.3 below.
Now let us make a few comments which concern the restricted dual
![]() $Y_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
of the full, completed, Yangian
$Y_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
of the full, completed, Yangian
![]() $Y_{\hbar }\mathfrak {g}$
. Since
$Y_{\hbar }\mathfrak {g}$
. Since
![]() $Y_{\hbar }\mathfrak {g}$
is an
$Y_{\hbar }\mathfrak {g}$
is an
![]() $\mathbb {N}$
-graded topological Hopf algebra over
$\mathbb {N}$
-graded topological Hopf algebra over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, the formalism of Section 2.3 implies that
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, the formalism of Section 2.3 implies that
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is a
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is a
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra, which provides a flat deformation of the algebra
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra, which provides a flat deformation of the algebra
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
over
$U({\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. In particular, there is an isomorphism of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. In particular, there is an isomorphism of
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
However,
![]() $Y_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is not itself a topological Hopf algebra over
$Y_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is not itself a topological Hopf algebra over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
with respect to the
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
with respect to the
![]() ${\hbar }$
-adic topology. It is, however, naturally a subalgebra of the topological Hopf algebra
${\hbar }$
-adic topology. It is, however, naturally a subalgebra of the topological Hopf algebra
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. This is made explicit by the below result.
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. This is made explicit by the below result.
Proposition 6.2 The
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear map
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear map
is an injective homomorphism of
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras.
Proof Since
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
is a
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
is a
![]() $\mathbb {Z}$
-graded Hopf subalgebra of
$\mathbb {Z}$
-graded Hopf subalgebra of
![]() $Y_{\hbar }\mathfrak {g}$
, the map
$Y_{\hbar }\mathfrak {g}$
, the map
![]() $f\mapsto f|_{{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}}$
respects the underlying
$f\mapsto f|_{{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}}$
respects the underlying
![]() $\mathbb {Z}$
-graded algebra structures. Moreover, if
$\mathbb {Z}$
-graded algebra structures. Moreover, if
![]() $f\in Y_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
vanishes on the basis
$f\in Y_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
vanishes on the basis
![]() $B({\hbar } {G})$
from Proposition 5.2, then it vanishes on the basis
$B({\hbar } {G})$
from Proposition 5.2, then it vanishes on the basis
![]() $B( {G})$
of
$B( {G})$
of
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
as
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
as
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
is torsion-free. This yields the injectivity.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
is torsion-free. This yields the injectivity.
Remark 6.3 Let
![]() $\mathbf {J}$
be as in (5.2). Then, since
$\mathbf {J}$
be as in (5.2). Then, since
![]() $\mathbf {J}$
satisfies
$\mathbf {J}$
satisfies
every
![]() $f\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is automatically continuous with respect to the
$f\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is automatically continuous with respect to the
![]() $\mathbf {J}$
-adic topology on
$\mathbf {J}$
-adic topology on
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
, and so uniquely extends to an element of the associated topological dual
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
, and so uniquely extends to an element of the associated topological dual
![]() $Y_{\hbar }\mathfrak {g}{\vphantom {)}}^{\circ }$
to
$Y_{\hbar }\mathfrak {g}{\vphantom {)}}^{\circ }$
to
![]() $Y_{\hbar }\mathfrak {g}^\prime $
(see Section 5.1 and Remark 5.4). In this sense, the notion of duality considered here is compatible with that for a general quantized enveloping algebra
$Y_{\hbar }\mathfrak {g}^\prime $
(see Section 5.1 and Remark 5.4). In this sense, the notion of duality considered here is compatible with that for a general quantized enveloping algebra
![]() $U_{\hbar }\mathfrak {b}$
outlined in Section 5.1, despite the fact that we did not need to leave the category of topological Hopf algebras over
$U_{\hbar }\mathfrak {b}$
outlined in Section 5.1, despite the fact that we did not need to leave the category of topological Hopf algebras over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
to define
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
to define
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
.
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
.
Remark 6.4 An alternative description of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
using the formalism of Remark 5.1 can be found in [Reference Etingof and Kazhdan12, Section 3.1].
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
using the formalism of Remark 5.1 can be found in [Reference Etingof and Kazhdan12, Section 3.1].
6.2 Chevalley involution and
 $\mathfrak {g}$
-action
$\mathfrak {g}$
-action
We now make a handful of simple observations which will play an important role in the remainder of this article. In what follows, we shall freely make use of the fact that
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
can be naturally viewed as a subspace of
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
can be naturally viewed as a subspace of
![]() $\mathrm {Hom}_{\mathbb {C}[{\hbar }]}({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}),\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])$
.
$\mathrm {Hom}_{\mathbb {C}[{\hbar }]}({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}),\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])$
.
Since the Chevalley involution
![]() $\omega $
defined in Lemma 3.3 is an anti-automorphism of the graded Hopf algebra
$\omega $
defined in Lemma 3.3 is an anti-automorphism of the graded Hopf algebra
![]() $Y_{\hbar }(\mathfrak {g})$
, it follows from the definition of
$Y_{\hbar }(\mathfrak {g})$
, it follows from the definition of
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
(or, alternatively, from Proposition 5.2) that it restricts to an anti-automorphism of the graded Hopf algebra
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
(or, alternatively, from Proposition 5.2) that it restricts to an anti-automorphism of the graded Hopf algebra
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
, which we again denote by
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
, which we again denote by
![]() $\omega $
. Consequently, the transpose
$\omega $
. Consequently, the transpose
![]() $\omega ^t$
of
$\omega ^t$
of
![]() $\omega $
, uniquely determined by
$\omega $
, uniquely determined by
is an involutive Hopf algebra anti-automorphism of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. We call
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. We call
![]() $\omega ^t$
the Chevalley involution of
$\omega ^t$
the Chevalley involution of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
.
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
.
Next, recall that the adjoint action of
![]() $\mathfrak {g}$
on
$\mathfrak {g}$
on
![]() $Y_{\hbar }(\mathfrak {g})$
preserves the Drinfeld–Gavarini subalgebra
$Y_{\hbar }(\mathfrak {g})$
preserves the Drinfeld–Gavarini subalgebra
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
. Since each graded component
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
. Since each graded component
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})_k$
is also a submodule, the restricted dual
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})_k$
is also a submodule, the restricted dual
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is a
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is a
![]() $\mathfrak {g}$
-module equipped with the coadjoint action
$\mathfrak {g}$
-module equipped with the coadjoint action
We now introduce a topological Q-grading on
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
compatible with the above action which is analogous to that obtained for
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
compatible with the above action which is analogous to that obtained for
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
in Section 4.2. For each
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
in Section 4.2. For each
![]() $\beta \in Q$
, define the closed
$\beta \in Q$
, define the closed
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-submodule
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-submodule
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _\beta \subset {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
by
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _\beta \subset {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
by
where
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]_\alpha $
is
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]_\alpha $
is
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
if
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
if
![]() $\alpha =0$
and is
$\alpha =0$
and is
![]() $\{0\}$
otherwise. It is easy to see that
$\{0\}$
otherwise. It is easy to see that
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _\beta $
is just the
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _\beta $
is just the
![]() $\beta $
-weight space of
$\beta $
-weight space of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
with respect to the
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
with respect to the
![]() $\mathfrak {g}$
-module structure introduced above. That is, one has
$\mathfrak {g}$
-module structure introduced above. That is, one has
As
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is Q-graded as a Hopf algebra, the direct sum
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
is Q-graded as a Hopf algebra, the direct sum
is a Q-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-subalgebra of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-subalgebra of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. Moreover, the counit, coproduct, and antipode of
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. Moreover, the counit, coproduct, and antipode of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
are all Q-graded, degree zero, maps. It is not difficult to prove that
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
are all Q-graded, degree zero, maps. It is not difficult to prove that
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _Q$
is a dense subalgebra of
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _Q$
is a dense subalgebra of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
whose subspace topology coincides with its
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
whose subspace topology coincides with its
![]() ${\hbar }$
-adic topology. Hence, we obtain the following result:
${\hbar }$
-adic topology. Hence, we obtain the following result:
Corollary 6.5
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is Q-graded as a topological Hopf algebra over
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is Q-graded as a topological Hopf algebra over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
.
6.3 Classical duality
We now wish to identify the graded dual
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
of the
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
of the
![]() $\mathbb {N}$
-graded Hopf algebra
$\mathbb {N}$
-graded Hopf algebra
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
with the enveloping algebra
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
with the enveloping algebra
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
, where we recall that
$U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
, where we recall that
![]() ${\mathfrak {t}}_{\scriptscriptstyle {-}}=t^{-1}\mathfrak {g}[t^{-1}]$
.
${\mathfrak {t}}_{\scriptscriptstyle {-}}=t^{-1}\mathfrak {g}[t^{-1}]$
.
To formulate this result optimally, we must first give a few preliminary remarks. To begin, we note that the semiclassical limit of the Chevalley involution
![]() $\omega ^t$
of
$\omega ^t$
of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
coincides, by definition, with the transpose
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
coincides, by definition, with the transpose
![]() $\dot {\omega }^t$
of the automorphism
$\dot {\omega }^t$
of the automorphism
![]() $\dot {\omega }$
of
$\dot {\omega }$
of
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
given on
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
given on
![]() ${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}$
by
${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}$
by
where
![]() $\bar {\omega }$
is as in (3.9). Similarly, the coadjoint action of
$\bar {\omega }$
is as in (3.9). Similarly, the coadjoint action of
![]() $\mathfrak {g}$
on
$\mathfrak {g}$
on
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
introduced in Section 6.2 specializes to an action of
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
introduced in Section 6.2 specializes to an action of
![]() $\mathfrak {g}$
on
$\mathfrak {g}$
on
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
. By definition, this action is dual to that of
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
. By definition, this action is dual to that of
![]() $\mathfrak {g}$
on
$\mathfrak {g}$
on
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
inherited from the adjoint action of
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
inherited from the adjoint action of
![]() $\mathfrak {g}$
on
$\mathfrak {g}$
on
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
.
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})$
.
On the other hand, the Chevalley involution
![]() $\bar \omega $
of
$\bar \omega $
of
![]() $U(\mathfrak {g}[t^{\pm 1}])$
, defined as in (3.9) with r taking values in
$U(\mathfrak {g}[t^{\pm 1}])$
, defined as in (3.9) with r taking values in
![]() $\mathbb {Z}$
, and the adjoint action of
$\mathbb {Z}$
, and the adjoint action of
![]() $\mathfrak {g}$
on
$\mathfrak {g}$
on
![]() $U(\mathfrak {g}[t^{\pm 1}])$
both preserve
$U(\mathfrak {g}[t^{\pm 1}])$
both preserve
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
. The resulting involution and
$U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
. The resulting involution and
![]() $\mathfrak {g}$
-module structure on
$\mathfrak {g}$
-module structure on
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
will be compared to those of
$U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
will be compared to those of
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
described in the previous paragraph in (3) of Proposition 6.6.
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
described in the previous paragraph in (3) of Proposition 6.6.
Consider now the standard symmetric algebra grading
where
![]() $\mathsf {S}^{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
is the nth symmetric power of
$\mathsf {S}^{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
is the nth symmetric power of
![]() ${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}$
, as in (5.4). Since
${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}$
, as in (5.4). Since
![]() $\mathsf {S}^{1}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})={\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}$
, every linear functional f in
$\mathsf {S}^{1}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})={\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}$
, every linear functional f in
![]() $({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\ast $
trivially extends to an element of
$({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\ast $
trivially extends to an element of
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\ast $
satisfying
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\ast $
satisfying
![]() $f(\mathsf {S}^{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}))=0$
for all
$f(\mathsf {S}^{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}))=0$
for all
![]() $n\neq 1$
, which is contained in
$n\neq 1$
, which is contained in
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
provided
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
provided
![]() $f\in ({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
. That is, we have
$f\in ({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
. That is, we have
![]() $({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star \subset \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
. In addition, we have a homogeneous, degree zero, isomorphism of graded vector spaces
$({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star \subset \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
. In addition, we have a homogeneous, degree zero, isomorphism of graded vector spaces
where
![]() $\mathsf {Res}_{\scriptscriptstyle -}$
and
$\mathsf {Res}_{\scriptscriptstyle -}$
and
![]() $\langle \,, \,\rangle $
are as defined in Section 2.5. With the above at our disposal, we are now prepared to identify
$\langle \,, \,\rangle $
are as defined in Section 2.5. With the above at our disposal, we are now prepared to identify
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
and
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
and
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
.
$U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
.
Proposition 6.6 The restricted dual
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
has the following properties:
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
has the following properties:
-
(1)
 $({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
is the Lie algebra of primitive elements in
$({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
is the Lie algebra of primitive elements in
 $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
, with bracket
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
, with bracket  $$ \begin{align*} [f,g]=(f\otimes g) \circ {\hbar}\delta_{\scriptscriptstyle +} \quad \forall \quad f,g\in ({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}})^\star. \end{align*} $$
$$ \begin{align*} [f,g]=(f\otimes g) \circ {\hbar}\delta_{\scriptscriptstyle +} \quad \forall \quad f,g\in ({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}})^\star. \end{align*} $$
-
(2)
 $\mathsf {Res}_{\scriptscriptstyle -}^{\hbar }$
uniquely extends to an isomorphism of graded Hopf algebras
$\mathsf {Res}_{\scriptscriptstyle -}^{\hbar }$
uniquely extends to an isomorphism of graded Hopf algebras 
-
(3)
 $\varphi $
is a
$\varphi $
is a
 $\mathfrak {g}$
-module intertwiner commuting with Chevalley involutions.
$\mathfrak {g}$
-module intertwiner commuting with Chevalley involutions.
Parts (1) and (2) of this proposition can be viewed as a variant of [Reference Kamnitzer, Webster, Weekes and Yacobi25, Corollary 3.4] applied to a restricted version of the setting in [Reference Kamnitzer, Webster, Weekes and Yacobi25, Section 3E]. They can be seen as a consequence of a graded generalization of (a special case of) Theorem 4.8 in [Reference Gavarini20]. It is not difficult to prove this variant directly using a fairly general argument, as we illustrate below.
Proof of (1)
An element
![]() $f\in \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
is primitive precisely when it satisfies
$f\in \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
is primitive precisely when it satisfies
Since the counit
![]() $\varepsilon $
of
$\varepsilon $
of
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
vanishes on
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
vanishes on
![]() $\mathbb {J}=\bigoplus _{n>0}\mathsf {S}^{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
, it follows readily that f must vanish on
$\mathbb {J}=\bigoplus _{n>0}\mathsf {S}^{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
, it follows readily that f must vanish on
![]() $\mathbb {J}^2=\bigoplus _{n>1}\mathsf {S}^{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
. Moreover, the above condition gives
$\mathbb {J}^2=\bigoplus _{n>1}\mathsf {S}^{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
. Moreover, the above condition gives
![]() $f(1)=2f(1)$
, and hence f vanishes on
$f(1)=2f(1)$
, and hence f vanishes on
![]() $\mathbb {C}$
. It follows that
$\mathbb {C}$
. It follows that
![]() $f\in \mathsf {S}^{1}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {(}}^\star =({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
.
$f\in \mathsf {S}^{1}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {(}}^\star =({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
.
Conversely, if
![]() $f\in ({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
, then
$f\in ({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
, then
![]() $\Delta (f)$
vanishes on
$\Delta (f)$
vanishes on
![]() $\mathsf {S}^{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})\otimes \mathsf {S}^{m}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
unless
$\mathsf {S}^{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})\otimes \mathsf {S}^{m}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
unless
![]() $n+m=1$
, and on
$n+m=1$
, and on
![]() ${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}\otimes \mathbb {C}$
and
${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}\otimes \mathbb {C}$
and
![]() $\mathbb {C}\otimes {\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}$
the identity (6.1) trivially holds. This completes the proof that the Lie algebra
$\mathbb {C}\otimes {\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}$
the identity (6.1) trivially holds. This completes the proof that the Lie algebra
![]() $\mathrm {Prim}\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
coincides with
$\mathrm {Prim}\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
coincides with
![]() $({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
as a vector space. Let us now prove that its bracket is given by
$({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
as a vector space. Let us now prove that its bracket is given by
Since
![]() $[f,g]\in ({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
, it is enough to establish this equality on
$[f,g]\in ({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
, it is enough to establish this equality on
![]() ${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}$
. By definition, we have
${\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}$
. By definition, we have
It thus suffices to prove that ![]() has image in
has image in
![]() $\mathrm {Ker}(f\otimes g)$
. As
$\mathrm {Ker}(f\otimes g)$
. As
![]() $Y_{\hbar }(\mathfrak {g})$
is a quantization of
$Y_{\hbar }(\mathfrak {g})$
is a quantization of
![]() $({\mathfrak {t}}_{\scriptscriptstyle {+}},\delta _{\scriptscriptstyle +})$
, we have
$({\mathfrak {t}}_{\scriptscriptstyle {+}},\delta _{\scriptscriptstyle +})$
, we have
where we recall that
![]() $\mu =\unicode{x3bd} ^{-1}$
, with
$\mu =\unicode{x3bd} ^{-1}$
, with
![]() $\unicode{x3bd} $
as in (3.13). Applying
$\unicode{x3bd} $
as in (3.13). Applying
![]() $\dot {\mathsf {q}}\otimes \dot {\mathsf {q}}$
and taking note of (5.3), we obtain
$\dot {\mathsf {q}}\otimes \dot {\mathsf {q}}$
and taking note of (5.3), we obtain
which completes the proof of (1).
Proof of (2)
Consider now (2). By Part (1),
![]() $\mathsf {Res}_{\scriptscriptstyle -}^{\hbar }$
is an isomorphism of graded Lie algebras
$\mathsf {Res}_{\scriptscriptstyle -}^{\hbar }$
is an isomorphism of graded Lie algebras ![]() . By the universal property of
. By the universal property of
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
, it extends uniquely to a homomorphism of graded Hopf algebras
$U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
, it extends uniquely to a homomorphism of graded Hopf algebras
which is necessarily injective (by [Reference Montgomery37, Lemma 5.3.3], for instance). As the finite-dimensional graded components
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {-}})_{-n}$
and
$U({\mathfrak {t}}_{\scriptscriptstyle {-}})_{-n}$
and
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star _{-n}=\mathsf {S}_{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {(}}^\ast $
have the same dimension for each
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star _{-n}=\mathsf {S}_{n}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {(}}^\ast $
have the same dimension for each
![]() $n\in \mathbb {N}$
, it follows that
$n\in \mathbb {N}$
, it follows that
![]() $\varphi $
is an isomorphism.
$\varphi $
is an isomorphism.
Proof of (3)
If
![]() $x\in {\mathfrak {t}}_{\scriptscriptstyle {-}}$
, then
$x\in {\mathfrak {t}}_{\scriptscriptstyle {-}}$
, then
![]() $\varphi (\bar \omega (x))$
is the element of
$\varphi (\bar \omega (x))$
is the element of
![]() $({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
determined by
$({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
determined by
where the second equality follows from the fact that the bilinear form
![]() $(\,,\,)$
on
$(\,,\,)$
on
![]() $\mathfrak {g}$
is
$\mathfrak {g}$
is
![]() $\omega $
-invariant. As
$\omega $
-invariant. As
![]() $({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
is stable under
$({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
is stable under
![]() $\dot \omega ^t$
and
$\dot \omega ^t$
and
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
is generated by
$U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
is generated by
![]() ${\mathfrak {t}}_{\scriptscriptstyle {-}}$
, we may conclude that
${\mathfrak {t}}_{\scriptscriptstyle {-}}$
, we may conclude that
![]() $\varphi \circ \bar \omega =\dot \omega ^t \circ \varphi $
.
$\varphi \circ \bar \omega =\dot \omega ^t \circ \varphi $
.
Similarly, if
![]() $x\in \mathfrak {g}$
and
$x\in \mathfrak {g}$
and
![]() $y\in {\mathfrak {t}}_{\scriptscriptstyle {-}}$
, then
$y\in {\mathfrak {t}}_{\scriptscriptstyle {-}}$
, then
![]() $\varphi ([x,y])\in ({{\hbar }{\mathfrak {t}}}_{\scriptscriptstyle {+}})^\star $
is determined by
$\varphi ([x,y])\in ({{\hbar }{\mathfrak {t}}}_{\scriptscriptstyle {+}})^\star $
is determined by
On the other hand, since
![]() $\mathbb {J}^k$
is a
$\mathbb {J}^k$
is a
![]() $\mathfrak {g}$
-submodule of
$\mathfrak {g}$
-submodule of
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
for each
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
for each
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $x \cdot \varphi (y)$
also belongs to
$x \cdot \varphi (y)$
also belongs to
![]() $({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
. Moreover, we have
$({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
. Moreover, we have
where we have used that
![]() $S(x)\cdot {\hbar } z-{\hbar }[z,x]\in \mathbb {J}^2\subset \mathrm {Ker}(\varphi (y))$
, which is proven analogously to (6.2). Since
$S(x)\cdot {\hbar } z-{\hbar }[z,x]\in \mathbb {J}^2\subset \mathrm {Ker}(\varphi (y))$
, which is proven analogously to (6.2). Since
![]() $\mathfrak {g}$
acts on both
$\mathfrak {g}$
acts on both
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
and
$U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
and
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
by derivations and
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
by derivations and
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
is generated by
$U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
is generated by
![]() ${\mathfrak {t}}_{\scriptscriptstyle {-}}$
, the above computation proves that
${\mathfrak {t}}_{\scriptscriptstyle {-}}$
, the above computation proves that
![]() $\varphi $
is a
$\varphi $
is a
![]() $\mathfrak {g}$
-module homomorphism.
$\mathfrak {g}$
-module homomorphism.
6.4
 ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
as a quantization
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
as a quantization
Since the dual Yangian
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is a
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is a
![]() $\mathbb {Z}$
-graded topologically free Hopf algebra over
$\mathbb {Z}$
-graded topologically free Hopf algebra over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
with semiclassical limit that, by Proposition 6.6, can be identified with
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
with semiclassical limit that, by Proposition 6.6, can be identified with
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
as a graded Hopf algebra, it is a quantized enveloping algebra which provides a homogeneous quantization of a
$U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
as a graded Hopf algebra, it is a quantized enveloping algebra which provides a homogeneous quantization of a
![]() $\mathbb {Z}$
-graded Lie bialgebra structure
$\mathbb {Z}$
-graded Lie bialgebra structure
![]() $({\mathfrak {t}}_{\scriptscriptstyle {-}},\delta )$
on the graded Lie algebra
$({\mathfrak {t}}_{\scriptscriptstyle {-}},\delta )$
on the graded Lie algebra
![]() ${\mathfrak {t}}_{\scriptscriptstyle {-}}=t^{-1}\mathfrak {g}[t^{-1}]$
.
${\mathfrak {t}}_{\scriptscriptstyle {-}}=t^{-1}\mathfrak {g}[t^{-1}]$
.
The following theorem asserts that this Lie bialgebra structure on
![]() ${\mathfrak {t}}_{\scriptscriptstyle {-}}$
is precisely that associated with the Manin triple
${\mathfrak {t}}_{\scriptscriptstyle {-}}$
is precisely that associated with the Manin triple
![]() $(\mathfrak {t},{\mathfrak {t}}_{\scriptscriptstyle {+}},{\mathfrak {t}}_{\scriptscriptstyle {-}})$
from Section 2.5.
$(\mathfrak {t},{\mathfrak {t}}_{\scriptscriptstyle {+}},{\mathfrak {t}}_{\scriptscriptstyle {-}})$
from Section 2.5.
Theorem 6.7
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is a homogeneous quantization of the Lie bialgebra
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is a homogeneous quantization of the Lie bialgebra
![]() $({\mathfrak {t}}_{\scriptscriptstyle {-}},\delta _{\scriptscriptstyle -})$
.
$({\mathfrak {t}}_{\scriptscriptstyle {-}},\delta _{\scriptscriptstyle -})$
.
Proof In light of the above discussion, the definition
![]() $\delta _{\scriptscriptstyle -}$
given in Section 2.5, and the identification of Proposition 6.6, it is sufficient to prove that the Lie bialgebra structure on
$\delta _{\scriptscriptstyle -}$
given in Section 2.5, and the identification of Proposition 6.6, it is sufficient to prove that the Lie bialgebra structure on
![]() ${\mathfrak {t}}_{\scriptscriptstyle {-}}\cong ({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
quantized by
${\mathfrak {t}}_{\scriptscriptstyle {-}}\cong ({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
quantized by
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
has cobracket
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
has cobracket
![]() $\delta $
given by
$\delta $
given by
By definition,
![]() $\delta $
is given by the formula
$\delta $
is given by the formula
where
![]() $\hat f\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is any lift of
$\hat f\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is any lift of
![]() $f\in ({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
and m is the product on
$f\in ({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
and m is the product on
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
. For any two elements
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
. For any two elements
![]() $x,y\in {\mathfrak {t}}_{\scriptscriptstyle {+}}$
, we have
$x,y\in {\mathfrak {t}}_{\scriptscriptstyle {+}}$
, we have
which implies the desired result:
 $$ \begin{align*} (\delta(f)-&f\circ {\hbar}^{-1}[,])({\hbar} x\otimes {\hbar} y)\\ &=\hat{f}([\mu(x),{\hbar}\mu(y)]-{\hbar}\mu[x,y])\quad\mod {\hbar}\mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt]=0.\\[-37pt] \end{align*} $$
$$ \begin{align*} (\delta(f)-&f\circ {\hbar}^{-1}[,])({\hbar} x\otimes {\hbar} y)\\ &=\hat{f}([\mu(x),{\hbar}\mu(y)]-{\hbar}\mu[x,y])\quad\mod {\hbar}\mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt]=0.\\[-37pt] \end{align*} $$
6.5 The dual triangular decomposition
Our main goal in this subsection is to establish a triangular decomposition for
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
dual to that for
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
dual to that for
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
established in Corollaries 5.5 and 5.6 (see also Remark 5.7). Along the way, we shall identify a family of generators for
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
established in Corollaries 5.5 and 5.6 (see also Remark 5.7). Along the way, we shall identify a family of generators for
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
(see Lemma 6.8).
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
(see Lemma 6.8).
For each choice of the symbol
![]() $\chi $
, consider the restricted dual
$\chi $
, consider the restricted dual
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
of the
${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
of the
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}$
. By Corollaries 2.9 and 5.5, this is a
${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}$
. By Corollaries 2.9 and 5.5, this is a
![]() $\mathbb {Z}$
-graded topologically free
$\mathbb {Z}$
-graded topologically free
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module with semiclassical limit equal to the graded dual
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module with semiclassical limit equal to the graded dual
of the symmetric algebra
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}^\chi )$
. Moreover, by Remark 2.8,
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}^\chi )$
. Moreover, by Remark 2.8,
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
coincides with the
${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
coincides with the
![]() ${\hbar }$
-adic completion of the graded dual to
${\hbar }$
-adic completion of the graded dual to
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\chi }(\mathfrak {g})$
taken in the category of
${\dot {\mathsf {Y}}}_{\hbar }^{\chi }(\mathfrak {g})$
taken in the category of
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-modules. Now let
$\mathbb {C}[{\hbar }]$
-modules. Now let
![]() $\pi ^\chi :{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\to {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}$
denote the
$\pi ^\chi :{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\to {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}$
denote the
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear projection associated with the identification of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear projection associated with the identification of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
with
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
with
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{+}\mathfrak {g}\otimes {\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}\otimes {\dot {\mathsf {Y}}}_{\hbar }^{-}\mathfrak {g}$
established in Remark 5.7. That is, we have
${\dot {\mathsf {Y}}}_{\hbar }^{+}\mathfrak {g}\otimes {\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}\otimes {\dot {\mathsf {Y}}}_{\hbar }^{-}\mathfrak {g}$
established in Remark 5.7. That is, we have
Taking the transpose of
![]() $\pi ^\chi $
yields a
$\pi ^\chi $
yields a
![]() $\mathbb {Z}$
-graded embedding of
$\mathbb {Z}$
-graded embedding of
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
with image consisting of precisely those
![]() $g\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
for which
$g\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
for which
![]() $g\circ \pi ^\chi =g$
. Note that if
$g\circ \pi ^\chi =g$
. Note that if
![]() ${\hbar }^ng$
is contained in this image for some
${\hbar }^ng$
is contained in this image for some
![]() $n\in \mathbb {N}$
, then g itself is, and so the subspace topology on
$n\in \mathbb {N}$
, then g itself is, and so the subspace topology on
![]() $(\pi ^\chi )^t({\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star )$
coincides with its
$(\pi ^\chi )^t({\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star )$
coincides with its
![]() ${\hbar }$
-adic topology. Furthermore, the semiclassical limit of
${\hbar }$
-adic topology. Furthermore, the semiclassical limit of
![]() $(\pi ^\chi )^t$
is the embedding
$(\pi ^\chi )^t$
is the embedding
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}^\chi ){\vphantom {)}}^\star \hookrightarrow \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
induced by the projection
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}^\chi ){\vphantom {)}}^\star \hookrightarrow \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
induced by the projection ![]() .
.
We shall henceforth adopt the viewpoint that
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
is a
${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
is a
![]() $\mathbb {Z}$
-graded topological submodule of
$\mathbb {Z}$
-graded topological submodule of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
, with the above identification assumed. We further note that the Chevalley involution
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
, with the above identification assumed. We further note that the Chevalley involution
![]() $\omega ^t$
of
$\omega ^t$
of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
satisfies
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
satisfies
Let us now identify a set of elements which generate
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
as a topological
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
as a topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra. These generators are constructed so as to naturally correspond to the coefficients of the
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra. These generators are constructed so as to naturally correspond to the coefficients of the
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
-valued series
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
-valued series
![]() $\dot {h}_i(u)$
and
$\dot {h}_i(u)$
and
![]() $\dot {x}_\beta ^\pm (u)$
defined in Section 4.2, and such an identification will be made precise in the proof of Lemma 7.4 (see (7.2)).
$\dot {x}_\beta ^\pm (u)$
defined in Section 4.2, and such an identification will be made precise in the proof of Lemma 7.4 (see (7.2)).
Given
![]() $\beta \in Q$
, let
$\beta \in Q$
, let
![]() $\pi _{\beta }:{\dot {\mathsf {Y}}}_{\hbar }^{-}(\mathfrak {g})\to {\dot {\mathsf {Y}}}_{\hbar }^{-}(\mathfrak {g})_\beta $
denote the natural projection onto the
$\pi _{\beta }:{\dot {\mathsf {Y}}}_{\hbar }^{-}(\mathfrak {g})\to {\dot {\mathsf {Y}}}_{\hbar }^{-}(\mathfrak {g})_\beta $
denote the natural projection onto the
![]() $\beta $
-component of
$\beta $
-component of
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{-}(\mathfrak {g})$
. Since the
${\dot {\mathsf {Y}}}_{\hbar }^{-}(\mathfrak {g})$
. Since the
![]() $\mathbb {C}[{\hbar }]$
-module isomorphism
$\mathbb {C}[{\hbar }]$
-module isomorphism
is Q-graded and respects the underlying triangular decompositions, we have
We may thus compose
![]() with
with
![]() $\mathsf {Res}_{\scriptscriptstyle -}^{\hbar }(x_i^+t^{-k-1})\in ({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
, as defined above Proposition 6.6, for any fixed
$\mathsf {Res}_{\scriptscriptstyle -}^{\hbar }(x_i^+t^{-k-1})\in ({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})^\star $
, as defined above Proposition 6.6, for any fixed
![]() $k\in \mathbb {N}$
. This outputs a degree
$k\in \mathbb {N}$
. This outputs a degree
![]() $-k-1$
element
$-k-1$
element
where we work through the identification of
![]() $\mathrm {Hom}_{\mathbb {C}[{\hbar }]}^a ({\dot {\mathsf {Y}}}_{\hbar }^{-}(\mathfrak {g}),\mathbb {C}[{\hbar }])$
with the ath component
$\mathrm {Hom}_{\mathbb {C}[{\hbar }]}^a ({\dot {\mathsf {Y}}}_{\hbar }^{-}(\mathfrak {g}),\mathbb {C}[{\hbar }])$
with the ath component
![]() $\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}^a ({\dot {\mathsf {Y}}}_{\hbar }^{-\!}\mathfrak {g},\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])$
of
$\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}^a ({\dot {\mathsf {Y}}}_{\hbar }^{-\!}\mathfrak {g},\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt])$
of
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{-\!}\mathfrak {g}{\vphantom {)}}^\star $
(see Remark 2.8). We now enlarge this family of elements to a generating set for the
${\dot {\mathsf {Y}}}_{\hbar }^{-\!}\mathfrak {g}{\vphantom {)}}^\star $
(see Remark 2.8). We now enlarge this family of elements to a generating set for the
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
using the coadjoint action of
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
using the coadjoint action of
![]() $\mathfrak {g}$
on
$\mathfrak {g}$
on
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
and the Chevalley involution
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
and the Chevalley involution
![]() $\omega ^t$
from Section 6.2. For each
$\omega ^t$
from Section 6.2. For each
![]() $i\in \mathbf {I}$
,
$i\in \mathbf {I}$
,
![]() $\beta \in \Delta ^+$
, and
$\beta \in \Delta ^+$
, and
![]() $k\in \mathbb {N}$
, we introduce the degree
$k\in \mathbb {N}$
, we introduce the degree
![]() $-k-1$
elements
$-k-1$
elements
 $$ \begin{gather*} {\mathsf{h}}_{i,-k-1}=-x_i^- \cdot {\mathsf{X}}_{i,-k-1}^+,\\ {\mathsf{X}}_{\beta,-k-1}^+:=\mathbf{X}^\beta\cdot {\mathsf{X}}_{i(\beta),-k-1}^+\in {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star_\beta,\quad {\mathsf{X}}_{\beta,-k-1}^-:=\omega^t({\mathsf{X}}_{\beta,-k-1}^+)\in {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star_{-\beta}, \end{gather*} $$
$$ \begin{gather*} {\mathsf{h}}_{i,-k-1}=-x_i^- \cdot {\mathsf{X}}_{i,-k-1}^+,\\ {\mathsf{X}}_{\beta,-k-1}^+:=\mathbf{X}^\beta\cdot {\mathsf{X}}_{i(\beta),-k-1}^+\in {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star_\beta,\quad {\mathsf{X}}_{\beta,-k-1}^-:=\omega^t({\mathsf{X}}_{\beta,-k-1}^+)\in {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star_{-\beta}, \end{gather*} $$
where
![]() $i(\beta )\in \mathbf {I}$
and
$i(\beta )\in \mathbf {I}$
and
![]() $\mathbf {X}^\beta \in U({\mathfrak {n}}_{+})_{\beta -\alpha _{i(\beta )}}$
are as in (3.11). In the same spirit as in Section 4.2, we organize these elements into generating series in
$\mathbf {X}^\beta \in U({\mathfrak {n}}_{+})_{\beta -\alpha _{i(\beta )}}$
are as in (3.11). In the same spirit as in Section 4.2, we organize these elements into generating series in
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star [\kern-1.2pt\![u]\!\kern-1.2pt]$
by setting
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star [\kern-1.2pt\![u]\!\kern-1.2pt]$
by setting
for each
![]() $i\in \mathbf {I}$
and
$i\in \mathbf {I}$
and
![]() $\beta \in \Delta ^+$
. We then have the following lemma.
$\beta \in \Delta ^+$
. We then have the following lemma.
Lemma 6.8 The dual Yangian
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is topologically generated as a
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is topologically generated as a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra by the coefficients of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra by the coefficients of
![]() $\{{\mathsf {X}}_\beta ^\pm (u)\}_{\beta \in \Delta ^+}$
and
$\{{\mathsf {X}}_\beta ^\pm (u)\}_{\beta \in \Delta ^+}$
and
![]() $\{{\mathsf {h}}_i(u)\}_{i\in \mathbf {I}}$
. Moreover, their images under the quotient map
$\{{\mathsf {h}}_i(u)\}_{i\in \mathbf {I}}$
. Moreover, their images under the quotient map
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \twoheadrightarrow {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star /{\hbar }{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \cong U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
are given by
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \twoheadrightarrow {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star /{\hbar }{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \cong U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
are given by
Proof As
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is a flat deformation of the algebra
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is a flat deformation of the algebra
![]() $ U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
over
$ U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
and the elements
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
and the elements
![]() $h_i t^{-k-1}$
and
$h_i t^{-k-1}$
and
![]() $x_\beta ^\pm t^{-k-1}$
generate
$x_\beta ^\pm t^{-k-1}$
generate
![]() ${\mathfrak {t}}_{\scriptscriptstyle {-}}=t^{-1}\mathfrak {g}[t^{-1}]$
as a Lie algebra, it is sufficient to prove the second assertion of the proposition.
${\mathfrak {t}}_{\scriptscriptstyle {-}}=t^{-1}\mathfrak {g}[t^{-1}]$
as a Lie algebra, it is sufficient to prove the second assertion of the proposition.
That the element
![]() ${\mathsf {X}}_{ir}^+$
coincides with
${\mathsf {X}}_{ir}^+$
coincides with
![]() $x_i^+t^{r}$
modulo
$x_i^+t^{r}$
modulo
![]() ${\hbar }{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is an immediate consequence of its definition and the identification of
${\hbar }{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is an immediate consequence of its definition and the identification of
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
with
$U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
with
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star /{\hbar }{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \cong \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
provided by Part (2) of Proposition 6.6. The remaining equivalences now follow from the definitions of
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star /{\hbar }{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \cong \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
provided by Part (2) of Proposition 6.6. The remaining equivalences now follow from the definitions of
![]() $h_i$
and
$h_i$
and
![]() $x_\beta ^\pm $
(see (3.11)) and Part (3) of Proposition 6.6, which implies that the quotient map
$x_\beta ^\pm $
(see (3.11)) and Part (3) of Proposition 6.6, which implies that the quotient map
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \twoheadrightarrow U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
is a
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \twoheadrightarrow U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
is a
![]() $\mathfrak {g}$
-module homomorphism intertwining Chevalley involutions.
$\mathfrak {g}$
-module homomorphism intertwining Chevalley involutions.
Let us now turn toward establishing a triangular decomposition for the dual Yangian
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. Following the notation from Section 5.3, let us introduce the Lie subalgebras
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. Following the notation from Section 5.3, let us introduce the Lie subalgebras
![]() ${\mathfrak {t}}_{\scriptscriptstyle {-}}^\chi $
of
${\mathfrak {t}}_{\scriptscriptstyle {-}}^\chi $
of
![]() $\mathfrak {t}=t^{-1}\mathfrak {g}[t^{-1}]$
by setting
$\mathfrak {t}=t^{-1}\mathfrak {g}[t^{-1}]$
by setting
The below proposition provides a strengthening of the
![]() ${\hbar }$
-adic analogues of Proposition 3.2 and Theorem 4.2 (i) from [Reference Khoroshkin and Tolstoy32].
${\hbar }$
-adic analogues of Proposition 3.2 and Theorem 4.2 (i) from [Reference Khoroshkin and Tolstoy32].
Proposition 6.9
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
and
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
and
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
are
${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
are
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-subalgebras of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-subalgebras of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. Moreover:
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. Moreover:
-
(1)
 ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
is a flat deformation of the
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
is a flat deformation of the
 $\mathbb {Z}$
-graded algebra
$\mathbb {Z}$
-graded algebra
 $U({\mathfrak {t}}_{\scriptscriptstyle {-}}^\mp )$
over
$U({\mathfrak {t}}_{\scriptscriptstyle {-}}^\mp )$
over
 $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. In particular, there is an isomorphism of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. In particular, there is an isomorphism of
 $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
 $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules  $$ \begin{align*} {\dot{\mathsf{Y}}}_{\hbar}^{\pm}\mathfrak{g}{\vphantom{)}}^\star\cong U({\mathfrak{t}}_{\scriptscriptstyle{-}}^\mp)[\kern-1.2pt\![h]\!\kern-1.2pt]. \end{align*} $$
$$ \begin{align*} {\dot{\mathsf{Y}}}_{\hbar}^{\pm}\mathfrak{g}{\vphantom{)}}^\star\cong U({\mathfrak{t}}_{\scriptscriptstyle{-}}^\mp)[\kern-1.2pt\![h]\!\kern-1.2pt]. \end{align*} $$
-
(2)
 ${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
is commutative and isomorphic to
${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
is commutative and isomorphic to
 $U({\mathfrak {t}}_{\scriptscriptstyle {-}}^0)[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]\cong \mathsf {S}({\mathfrak {t}}_{\scriptscriptstyle {-}}^0)[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as a
$U({\mathfrak {t}}_{\scriptscriptstyle {-}}^0)[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]\cong \mathsf {S}({\mathfrak {t}}_{\scriptscriptstyle {-}}^0)[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
as a
 $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
 $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra. -
(3)
 ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
and
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
and
 ${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
are topologically generated as
${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
are topologically generated as
 $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras by the coefficients of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras by the coefficients of
 $\{{\mathsf {X}}_\beta ^\mp (u)\}_{\beta \in \Delta ^+}$
and
$\{{\mathsf {X}}_\beta ^\mp (u)\}_{\beta \in \Delta ^+}$
and
 $\{{\mathsf {h}}_i(u)\}_{i\in \mathbf {I}}$
, respectively.
$\{{\mathsf {h}}_i(u)\}_{i\in \mathbf {I}}$
, respectively.
Proof One can deduce that
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
is a subalgebra of
${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
is a subalgebra of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
using properties of the Yangian coproduct, as in [Reference Khoroshkin and Tolstoy32, Proposition 3.2]. We shall give an alternate simple proof of this fact in Section 7.3 which illustrates that it follows naturally from properties of
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
using properties of the Yangian coproduct, as in [Reference Khoroshkin and Tolstoy32, Proposition 3.2]. We shall give an alternate simple proof of this fact in Section 7.3 which illustrates that it follows naturally from properties of
![]() $\mathcal {R}(z)$
(see Corollary 7.7 and Remark 7.8).
$\mathcal {R}(z)$
(see Corollary 7.7 and Remark 7.8).
Let us complete the proof of the proposition assuming Corollary 7.7, which, as explained in Remark 7.8, also implies that the coefficients of
![]() $\{{\mathsf {X}}_\beta ^\mp (u)\}_{\beta \in \Delta ^+}$
and
$\{{\mathsf {X}}_\beta ^\mp (u)\}_{\beta \in \Delta ^+}$
and
![]() $\{{\mathsf {h}}_i(u)\}_{i\in \mathbf {I}}$
belong to
$\{{\mathsf {h}}_i(u)\}_{i\in \mathbf {I}}$
belong to
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\mp }\mathfrak {g}{\vphantom {)}}^\star $
and
${\dot {\mathsf {Y}}}_{\hbar }^{\mp }\mathfrak {g}{\vphantom {)}}^\star $
and
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
, respectively, and that
${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
, respectively, and that
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
is commutative.
${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
is commutative.
Proof of (1) and (2)
The graded Lie bialgebra isomorphism ![]() of Proposition 6.6 restricts to an isomorphism
of Proposition 6.6 restricts to an isomorphism ![]() . Since
. Since
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
is a subalgebra of
${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
is a subalgebra of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
, its semiclassical limit
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
, its semiclassical limit
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}^\chi ){\vphantom {)}}^\star $
is a
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}^\chi ){\vphantom {)}}^\star $
is a
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-subalgebra of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-subalgebra of
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {()}}^\star $
and not just a submodule. It follows from these observations that the graded Hopf algebra isomorphism
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {()}}^\star $
and not just a submodule. It follows from these observations that the graded Hopf algebra isomorphism
![]() $\varphi $
of Proposition 6.6 restricts to an injective
$\varphi $
of Proposition 6.6 restricts to an injective
![]() $\mathbb {Z}$
-graded algebra homomorphism
$\mathbb {Z}$
-graded algebra homomorphism
which is surjective by the same argument as used in the proof of Part (2) of Proposition 6.6. Since
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
is a
${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
is a
![]() $\mathbb {Z}$
-graded topologically free
$\mathbb {Z}$
-graded topologically free
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra with semiclassical limit
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra with semiclassical limit ![]() , taking
, taking
![]() $\chi =\pm $
recovers Part (1) of the proposition.
$\chi =\pm $
recovers Part (1) of the proposition.
As for Part (2), since
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
is a commutative topological
${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
is a commutative topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra containing
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra containing
![]() $\{{\mathsf {h}}_{ik}\}_{i\in \mathbf {I},k<0}$
(by Corollary 7.7), there is a
$\{{\mathsf {h}}_{ik}\}_{i\in \mathbf {I},k<0}$
(by Corollary 7.7), there is a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
uniquely determined by
![]() $\unicode{x3b7} (h_it^k)={\mathsf {h}}_{ik}$
for all
$\unicode{x3b7} (h_it^k)={\mathsf {h}}_{ik}$
for all
![]() $i\in \mathbf {I}$
and
$i\in \mathbf {I}$
and
![]() $k<0$
. By Lemma 6.8, the semiclassical limit
$k<0$
. By Lemma 6.8, the semiclassical limit
![]() of
of
![]() $\unicode{x3b7} $
satisfies
$\unicode{x3b7} $
satisfies
![]() for all
for all
![]() $i\in \mathbf {I}$
and
$i\in \mathbf {I}$
and
![]() $k<0$
, and thus coincides with the canonical isomorphism
$k<0$
, and thus coincides with the canonical isomorphism ![]() . Here, we have assumed the identification of
. Here, we have assumed the identification of
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star /{\hbar }{\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
with
${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star /{\hbar }{\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
with
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {-}}^0)$
provided by
$U({\mathfrak {t}}_{\scriptscriptstyle {-}}^0)$
provided by
![]() $\varphi _0$
from (6.5) above. As
$\varphi _0$
from (6.5) above. As
![]() $\mathsf {S}({\mathfrak {t}}_{\scriptscriptstyle {-}}^0)$
and
$\mathsf {S}({\mathfrak {t}}_{\scriptscriptstyle {-}}^0)$
and
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
are both topologically free, we can conclude from Lemma 2.1 that
${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
are both topologically free, we can conclude from Lemma 2.1 that
![]() $\unicode{x3b7} $
is an isomorphism of topological
$\unicode{x3b7} $
is an isomorphism of topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras.
Proof of (3)
For
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
, this follows from the definition of the isomorphism
${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
, this follows from the definition of the isomorphism
![]() $\unicode{x3b7} $
given in the proof of (2) above.
$\unicode{x3b7} $
given in the proof of (2) above.
Similarly, by Lemma 6.8 and Corollary 7.7,
![]() ${\mathsf {X}}_{\beta ,k}^\mp $
belongs to
${\mathsf {X}}_{\beta ,k}^\mp $
belongs to
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
and specializes to
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
and specializes to
![]() $x_\beta ^\mp t^k$
in
$x_\beta ^\mp t^k$
in
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star /{\hbar } {\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star \cong U({\mathfrak {t}}_{\scriptscriptstyle {-}}^\mp ) \subset U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
, for each
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star /{\hbar } {\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star \cong U({\mathfrak {t}}_{\scriptscriptstyle {-}}^\mp ) \subset U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
, for each
![]() $\beta \in \Delta ^+$
and
$\beta \in \Delta ^+$
and
![]() $k<0$
. Since the elements
$k<0$
. Since the elements
![]() $x_\beta ^\mp t^k$
generate the Lie algebra
$x_\beta ^\mp t^k$
generate the Lie algebra
![]() ${\mathfrak {t}}_{\scriptscriptstyle {-}}^\mp $
and, by Part (1),
${\mathfrak {t}}_{\scriptscriptstyle {-}}^\mp $
and, by Part (1),
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
is a flat deformation of the algebra
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
is a flat deformation of the algebra
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {-}}^\mp )$
over
$U({\mathfrak {t}}_{\scriptscriptstyle {-}}^\mp )$
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, this completes the proof of the proposition.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, this completes the proof of the proposition.
Remark 6.10 We caution that
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
is not generated by the elements
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
is not generated by the elements
![]() ${\mathsf {X}}_{i,-k-1}^\mp $
, for
${\mathsf {X}}_{i,-k-1}^\mp $
, for
![]() $i\in \mathbf {I}$
and
$i\in \mathbf {I}$
and
![]() $k\in \mathbb {N}$
, unless
$k\in \mathbb {N}$
, unless
![]() $\mathfrak {g}=\mathfrak {s}\mathfrak {l}_2$
, just as
$\mathfrak {g}=\mathfrak {s}\mathfrak {l}_2$
, just as
![]() $t^{-1}{\mathfrak {n}}_{\mp }[t^{-1}]$
is not generated as a Lie algebra by the elements
$t^{-1}{\mathfrak {n}}_{\mp }[t^{-1}]$
is not generated as a Lie algebra by the elements
![]() $x_i^\mp t^{-k-1}$
outside of the rank one case. In particular, the statement of Part (i) in [Reference Khoroshkin and Tolstoy32, Theorem 4.2], which is the analogue of Part (2) above, should be adjusted.
$x_i^\mp t^{-k-1}$
outside of the rank one case. In particular, the statement of Part (i) in [Reference Khoroshkin and Tolstoy32, Theorem 4.2], which is the analogue of Part (2) above, should be adjusted.
As an application of Lemma 2.1, Proposition 6.9, the decomposition ![]() , and the Poincaré–Birkhoff–Witt theorem for enveloping algebras, we obtain the following variant of Theorem 3.1(ii) in [Reference Khoroshkin and Tolstoy32].
, and the Poincaré–Birkhoff–Witt theorem for enveloping algebras, we obtain the following variant of Theorem 3.1(ii) in [Reference Khoroshkin and Tolstoy32].
Corollary 6.11 The multiplication map
is an isomorphism of
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules.
Remark 6.12 We note that for the statement of [Reference Khoroshkin and Tolstoy32, Theorem 3.1] to hold, the tensor product
![]() $\otimes $
must be taken to be a completion of the algebraic tensor product
$\otimes $
must be taken to be a completion of the algebraic tensor product
![]() $\otimes _{\mathbb {C}}$
compatible with the underlying
$\otimes _{\mathbb {C}}$
compatible with the underlying
![]() $\mathbb {Z}$
-filtrations.
$\mathbb {Z}$
-filtrations.
7
 $\mathrm {D}Y_{\hbar }\mathfrak {g}$
as a quantization
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
as a quantization
In this section, we construct a
![]() $\mathbb {Z}$
-graded topological Hopf algebra structure on
$\mathbb {Z}$
-graded topological Hopf algebra structure on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
which quantizes the graded Lie bialgebra structure on the loop algebra
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
which quantizes the graded Lie bialgebra structure on the loop algebra
![]() $\mathfrak {t}=\mathfrak {g}[t^{\pm 1}]$
defined in Section 2.5. This will be achieved in Theorem 7.5 using Proposition 7.1 and Corollary 7.3. As a consequence of these results, we obtain in Section 7.3 a characterization of the restricted duals
$\mathfrak {t}=\mathfrak {g}[t^{\pm 1}]$
defined in Section 2.5. This will be achieved in Theorem 7.5 using Proposition 7.1 and Corollary 7.3. As a consequence of these results, we obtain in Section 7.3 a characterization of the restricted duals
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
and
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
and
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
in terms of the universal R-matrix
${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
in terms of the universal R-matrix
![]() $\mathcal {R}(z)$
which completes the proof of Proposition 6.9.
$\mathcal {R}(z)$
which completes the proof of Proposition 6.9.
7.1 The morphism 
Henceforth, the notation ![]() will be used to denote the topological Hopf algebra
will be used to denote the topological Hopf algebra
![]() $({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star ){\vphantom {)}}^{\scriptscriptstyle \mathrm {cop}}$
over
$({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star ){\vphantom {)}}^{\scriptscriptstyle \mathrm {cop}}$
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. That is,
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. That is, ![]() coincides with the dual Yangian
coincides with the dual Yangian
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
as an algebra, and has coproduct
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
as an algebra, and has coproduct ![]() , counit
, counit ![]() , and antipode
, and antipode ![]() given by
given by

where m,
![]() $\iota $
, and S are the product, unit, and antipode of the Drinfeld–Gavarini Yangian
$\iota $
, and S are the product, unit, and antipode of the Drinfeld–Gavarini Yangian
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\subset Y_{\hbar }\mathfrak {g}$
(see Section 6.1). By Theorem 6.7,
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\subset Y_{\hbar }\mathfrak {g}$
(see Section 6.1). By Theorem 6.7, ![]() is a flat deformation of the enveloping algebra
is a flat deformation of the enveloping algebra
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {-}})=U(t^{-1}\mathfrak {g}[t^{-1}])$
over
$U({\mathfrak {t}}_{\scriptscriptstyle {-}})=U(t^{-1}\mathfrak {g}[t^{-1}])$
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
which provides a homogeneous quantization of the Lie bialgebra
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
which provides a homogeneous quantization of the Lie bialgebra
![]() $({\mathfrak {t}}_{\scriptscriptstyle {-}}, -\delta _{\scriptscriptstyle -})$
.
$({\mathfrak {t}}_{\scriptscriptstyle {-}}, -\delta _{\scriptscriptstyle -})$
.
Our present goal is to construct a homomorphism of
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras
which is compatible with both the formal shift operator
![]() $\Phi _z$
of Theorem 4.6 and the Hopf structures on
$\Phi _z$
of Theorem 4.6 and the Hopf structures on ![]() and
and
![]() $Y_{\hbar }\mathfrak {g}$
. This is achieved using the universal R-matrix
$Y_{\hbar }\mathfrak {g}$
. This is achieved using the universal R-matrix
![]() $\mathcal {R}(z)$
of the Yangian as follows. By Lemma 5.9,
$\mathcal {R}(z)$
of the Yangian as follows. By Lemma 5.9,
![]() $\mathcal {R}(z)$
is an element of
$\mathcal {R}(z)$
is an element of
![]() $({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\otimes Y_{\hbar }(\mathfrak {g}))[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
, and thus gives rise to a
$({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\otimes Y_{\hbar }(\mathfrak {g}))[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
, and thus gives rise to a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphism
Now recall that
![]() $\dot {h}_i(u),{\dot {x}}_\beta ^\pm (u)\in {\mathrm {D}}Y_{\hbar }\mathfrak {g}[\kern-1.2pt\![u]\!\kern-1.2pt]$
and
$\dot {h}_i(u),{\dot {x}}_\beta ^\pm (u)\in {\mathrm {D}}Y_{\hbar }\mathfrak {g}[\kern-1.2pt\![u]\!\kern-1.2pt]$
and ![]() are the generating series defined in Sections 4.2 and 6.5, respectively. In addition, we let
are the generating series defined in Sections 4.2 and 6.5, respectively. In addition, we let ![]() denote the canonical
denote the canonical
![]() ${\mathbb {C}}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
${\mathbb {C}}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
given by evaluating w to z. The following proposition asserts that ![]() indeed has the desired properties.
indeed has the desired properties.
Proposition 7.1
![]() has the following properties:
has the following properties:
-
(1) It is a homomorphism of
 $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras satisfying
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras satisfying 
-
(2) It is a
 $U(\mathfrak {g})$
-module homomorphism compatible with Chevalley involutions:
$U(\mathfrak {g})$
-module homomorphism compatible with Chevalley involutions: 
-
(3) Its restriction to
 ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}){\vphantom {)}}^\star $
is a
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}){\vphantom {)}}^\star $
is a
 $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
 $\mathbb {C}[{\hbar }]$
-algebra homomorphism
$\mathbb {C}[{\hbar }]$
-algebra homomorphism 
-
(4) For each
 $\beta \in \Delta ^+$
and
$\beta \in \Delta ^+$
and
 $i\in \mathbf {I}$
, one has
$i\in \mathbf {I}$
, one has 
Proof of (1)
This is a modification of the standard result that if H is a finite-dimensional quasitriangular Hopf algebra over a field
![]() $\mathbb {K}$
with R-matrix
$\mathbb {K}$
with R-matrix
![]() $R\in H\otimes _{\mathbb {K}}H$
, then the map
$R\in H\otimes _{\mathbb {K}}H$
, then the map
![]() $f\mapsto (f\otimes \mathbf {1}_H)R$
defines a homomorphism of Hopf algebras
$f\mapsto (f\otimes \mathbf {1}_H)R$
defines a homomorphism of Hopf algebras
![]() $(H^\ast ){\vphantom {)}}^{\scriptscriptstyle \mathrm {cop}}\to H$
(see, for instance, [Reference Chari and Pressley4, Section 4.2.B] or [Reference Radford39, Section 2]). The only novelty in the present setting is the appearance of the formal parameter z. Nonetheless, for the sake of completeness, we shall give a full proof.
$(H^\ast ){\vphantom {)}}^{\scriptscriptstyle \mathrm {cop}}\to H$
(see, for instance, [Reference Chari and Pressley4, Section 4.2.B] or [Reference Radford39, Section 2]). The only novelty in the present setting is the appearance of the formal parameter z. Nonetheless, for the sake of completeness, we shall give a full proof.
As the product on ![]() is the transpose of the coproduct
is the transpose of the coproduct
![]() $\Delta $
on
$\Delta $
on
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
and
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
and
![]() $\Delta \otimes \mathbf {1} (\mathcal {R}(z))=\mathcal {R}_{13}(z)\mathcal {R}_{23}(z)$
, we have
$\Delta \otimes \mathbf {1} (\mathcal {R}(z))=\mathcal {R}_{13}(z)\mathcal {R}_{23}(z)$
, we have
Since, in addition,
![]() $(\varepsilon \otimes \mathbf {1}) \mathcal {R}(z)=1$
, we can conclude that
$(\varepsilon \otimes \mathbf {1}) \mathcal {R}(z)=1$
, we can conclude that ![]() is a homomorphism of unital, associative
is a homomorphism of unital, associative
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras.
Let us now verify the coproduct identity ![]() on
on ![]() . Using the cabling identity
. Using the cabling identity
![]() $\mathbf {1}\otimes \Delta (\mathcal {R}(z))=\mathcal {R}_{13}(z)\mathcal {R}_{12}(z)$
, we obtain
$\mathbf {1}\otimes \Delta (\mathcal {R}(z))=\mathcal {R}_{13}(z)\mathcal {R}_{12}(z)$
, we obtain

Finally, the remaining two identities follow from the relations
![]() $(\mathbf {1}\otimes \varepsilon )\mathcal {R}(z)=1$
and
$(\mathbf {1}\otimes \varepsilon )\mathcal {R}(z)=1$
and
![]() $(S^{-1}\otimes \mathbf {1})\mathcal {R}(z)=(\mathbf {1} \otimes S)\mathcal {R}(z)$
. Indeed, for each
$(S^{-1}\otimes \mathbf {1})\mathcal {R}(z)=(\mathbf {1} \otimes S)\mathcal {R}(z)$
. Indeed, for each ![]() , we have
, we have

Proof of (2)
Since
![]() $\tau _z$
restricts to the identity on
$\tau _z$
restricts to the identity on
![]() $U(\mathfrak {g})$
, the intertwiner equation (3.20) implies that
$U(\mathfrak {g})$
, the intertwiner equation (3.20) implies that
![]() $\mathcal {R}(z)$
is a
$\mathcal {R}(z)$
is a
![]() $\mathfrak {g}$
-invariant element of
$\mathfrak {g}$
-invariant element of
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
:
$Y_{\hbar }(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
:
It follows readily from this fact, and the definition of the
![]() $\mathfrak {g}$
-module structure on
$\mathfrak {g}$
-module structure on ![]() introduced in Section 6.2, that
introduced in Section 6.2, that ![]() is a
is a
![]() $U(\mathfrak {g})$
-module homomorphism.
$U(\mathfrak {g})$
-module homomorphism.
Similarly, by Corollary 3.10, the Chevalley involution
![]() $\omega $
satisfies
$\omega $
satisfies
![]() $(\omega \otimes \omega ) \mathcal {R}(z)=\mathcal {R}(z)$
, and we thus have
$(\omega \otimes \omega ) \mathcal {R}(z)=\mathcal {R}(z)$
, and we thus have
Proof of (3)
Suppose that f is a degree k element of
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}){\vphantom {)}}^\star $
for some
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}){\vphantom {)}}^\star $
for some
![]() $k\in \mathbb {Z}$
. Then
$k\in \mathbb {Z}$
. Then
![]() $f\otimes \mathbf {1}:{\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\otimes Y_{\hbar }(\mathfrak {g}) \to Y_{\hbar }(\mathfrak {g})$
is homogeneous of degree k, and hence
$f\otimes \mathbf {1}:{\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})\otimes Y_{\hbar }(\mathfrak {g}) \to Y_{\hbar }(\mathfrak {g})$
is homogeneous of degree k, and hence
where
![]() $\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z=\prod _{n\in \mathbb {N}}(Y_{\hbar }(\mathfrak {g})^{\otimes 2})_n z^{-n}$
, as in Section 3.6. The assertion now follows from Part (3) of Theorem 3.8 and Lemma 5.9, which yield
$\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z=\prod _{n\in \mathbb {N}}(Y_{\hbar }(\mathfrak {g})^{\otimes 2})_n z^{-n}$
, as in Section 3.6. The assertion now follows from Part (3) of Theorem 3.8 and Lemma 5.9, which yield
Proof of (4)
Since ![]() is a
is a
![]() $U(\mathfrak {g})$
-module homomorphism intertwining Chevalley involutions, it is sufficient to establish that
$U(\mathfrak {g})$
-module homomorphism intertwining Chevalley involutions, it is sufficient to establish that
where we recall that
![]() ${\mathsf {X}}_{i,-k-1}^+$
was defined explicitly in (6.4). Since
${\mathsf {X}}_{i,-k-1}^+$
was defined explicitly in (6.4). Since
![]() $\varepsilon \otimes \mathbf {1}$
sends both
$\varepsilon \otimes \mathbf {1}$
sends both
![]() $\mathcal {R}^0(z)$
and
$\mathcal {R}^0(z)$
and
![]() $\mathcal {R}^+(z)$
to
$\mathcal {R}^+(z)$
to
![]() $1$
and
$1$
and
![]() ${\mathsf {X}}_{i,-k-1}^+$
vanishes on
${\mathsf {X}}_{i,-k-1}^+$
vanishes on
![]() ${\dot {\mathsf {Y}}}_{\hbar }^-(\mathfrak {g})_\beta $
for
${\dot {\mathsf {Y}}}_{\hbar }^-(\mathfrak {g})_\beta $
for
![]() $\beta \neq -\alpha _i$
, we have
$\beta \neq -\alpha _i$
, we have
Using (3.18), we deduce that the element
![]() $\mathcal {R}^-_{\alpha _i}(z)$
is given by
$\mathcal {R}^-_{\alpha _i}(z)$
is given by
 $$ \begin{align*} \mathcal{R}^-_{\alpha_i}(z)=\sum_{p\geq 0}\frac{\alpha_i(\zeta)\mathbf{T}(\zeta)^p}{(z\alpha_i(\zeta))^{p+1}} ({\hbar} x_{i,0}^- \otimes x_{i,0}^+)=\sum_{p\geq 0}\sum_{n=0}^p \binom{p}{n}(-1)^n {\hbar} x_{i,n}^-\otimes x_{i,p-n}^+z^{-p-1}, \end{align*} $$
$$ \begin{align*} \mathcal{R}^-_{\alpha_i}(z)=\sum_{p\geq 0}\frac{\alpha_i(\zeta)\mathbf{T}(\zeta)^p}{(z\alpha_i(\zeta))^{p+1}} ({\hbar} x_{i,0}^- \otimes x_{i,0}^+)=\sum_{p\geq 0}\sum_{n=0}^p \binom{p}{n}(-1)^n {\hbar} x_{i,n}^-\otimes x_{i,p-n}^+z^{-p-1}, \end{align*} $$
where we have used
![]() $\mathrm {ad}(\mathrm {T}(\zeta ))^p(x_{i,0}^\pm )=(\pm 1)^p \alpha _i(\zeta )^p x_{i,p}^\pm $
. This can be rewritten as
$\mathrm {ad}(\mathrm {T}(\zeta ))^p(x_{i,0}^\pm )=(\pm 1)^p \alpha _i(\zeta )^p x_{i,p}^\pm $
. This can be rewritten as
where the second equality is due to Part (1) of Theorem 4.6. As
![]() ${\mathsf {X}}_{i,-k-1}^+({\hbar } x_{i,n}^-)=\mathsf {Res}_{\scriptscriptstyle -}^{\hbar }(x_i^+t^{-k-1})({\hbar } x_{i}^-t^n)=-\delta _{kn}$
for all
${\mathsf {X}}_{i,-k-1}^+({\hbar } x_{i,n}^-)=\mathsf {Res}_{\scriptscriptstyle -}^{\hbar }(x_i^+t^{-k-1})({\hbar } x_{i}^-t^n)=-\delta _{kn}$
for all
![]() $k,n\in \mathbb {N}$
, this implies the identity (7.1).
$k,n\in \mathbb {N}$
, this implies the identity (7.1).
Remark 7.2 As ![]() and
and
![]() $\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
are
$\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
are
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras with
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras with
Part (3) of the proposition is equivalent to the assertion that ![]() is a
is a
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism ![]() .
.
Since ![]() has image in
has image in
![]() $\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
, we may compose it with
$\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
, we may compose it with
![]() $\mathscr{E}\mathscr{v}$
from (4.2) to obtain a
$\mathscr{E}\mathscr{v}$
from (4.2) to obtain a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
Our present goal is to apply Part (1) of Proposition 7.1 to interpret ![]() as a homomorphism of topological Hopf algebras, where the topological structure on the completed Yangian is that induced by the gradation topology on
as a homomorphism of topological Hopf algebras, where the topological structure on the completed Yangian is that induced by the gradation topology on
![]() $Y_{\hbar }\mathfrak {g}$
. To make this precise, let us define
$Y_{\hbar }\mathfrak {g}$
. To make this precise, let us define
![]() $\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {)}}^{\scriptscriptstyle (n)}$
, for any
$\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {)}}^{\scriptscriptstyle (n)}$
, for any
![]() $n\in \mathbb {N}$
, to be the formal completion of
$n\in \mathbb {N}$
, to be the formal completion of
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes n}$
with respect to its
$Y_{\hbar }(\mathfrak {g})^{\otimes n}$
with respect to its
![]() $\mathbb {N}$
-grading:
$\mathbb {N}$
-grading:
Equivalently, it is the completion of the
![]() $\mathbb {N}$
-graded topological
$\mathbb {N}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra
![]() $Y_{\hbar }\mathfrak {g}^{\otimes n}$
with respect to the filtration defining its gradation topology, as defined in Section 2.3. By [Reference Wendlandt41, Proposition A.1], this is a topologically free
$Y_{\hbar }\mathfrak {g}^{\otimes n}$
with respect to the filtration defining its gradation topology, as defined in Section 2.3. By [Reference Wendlandt41, Proposition A.1], this is a topologically free
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra containing
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra containing
![]() $Y_{\hbar }\mathfrak {g}^{\otimes n}$
as a subalgebra (see also [Reference Wendlandt41, Lemma 4.1] and Section 4.3 above). Furthermore, we can (and shall) view
$Y_{\hbar }\mathfrak {g}^{\otimes n}$
as a subalgebra (see also [Reference Wendlandt41, Lemma 4.1] and Section 4.3 above). Furthermore, we can (and shall) view
where
![]() $\otimes $
denotes the topological tensor product over
$\otimes $
denotes the topological tensor product over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
.
Next, observe that the
![]() $\mathbb {N}$
-graded Hopf algebra structure on
$\mathbb {N}$
-graded Hopf algebra structure on
![]() $Y_{\hbar }(\mathfrak {g})$
induces a topological Hopf structure on
$Y_{\hbar }(\mathfrak {g})$
induces a topological Hopf structure on
![]() $\widehat {Y_{\hbar }\mathfrak {g}}$
, equipped with the grading-completed tensor product. More precisely, as the multiplication m, coproduct
$\widehat {Y_{\hbar }\mathfrak {g}}$
, equipped with the grading-completed tensor product. More precisely, as the multiplication m, coproduct
![]() $\Delta $
, counit
$\Delta $
, counit
![]() $\varepsilon $
, and antipode S on
$\varepsilon $
, and antipode S on
![]() $Y_{\hbar }(\mathfrak {g})$
are
$Y_{\hbar }(\mathfrak {g})$
are
![]() $\mathbb {N}$
-graded, they uniquely extend to
$\mathbb {N}$
-graded, they uniquely extend to
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphisms
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphisms
which collectively satisfy the axioms of a Hopf algebra. Proposition 7.1 then admits the following corollary.
Corollary 7.3 The
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism ![]() is a morphism of topological Hopf algebras. That is, it satisfies
is a morphism of topological Hopf algebras. That is, it satisfies
In particular, one has ![]() .
.
Proof The counit and antipode relations are obtained by applying
![]() $\mathscr{E}\mathscr{v}$
to the corresponding relations of Part (1) of Proposition 7.1 and appealing to the identity
$\mathscr{E}\mathscr{v}$
to the corresponding relations of Part (1) of Proposition 7.1 and appealing to the identity ![]() . The idea now is that the relation
. The idea now is that the relation ![]() should follow by applying
should follow by applying
![]() $\mathscr{E}\mathscr{v}\otimes \mathscr{E}\mathscr{v}$
to both sides of the identity
$\mathscr{E}\mathscr{v}\otimes \mathscr{E}\mathscr{v}$
to both sides of the identity ![]() .
.
However, to make this precise, we must first make a few technical observations. Recall from (3.16) that
![]() $ {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)$
is the
$ {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)$
is the
![]() $\mathbb {Z}$
-graded subalgebra of
$\mathbb {Z}$
-graded subalgebra of
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes 2}[z;z^{-1}]\!\kern-1.2pt]$
with kth homogeneous component
$Y_{\hbar }(\mathfrak {g})^{\otimes 2}[z;z^{-1}]\!\kern-1.2pt]$
with kth homogeneous component
![]() $ z^k \widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z$
, where
$ z^k \widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z$
, where
Following Section 4.3, we shall write
![]() $\mathrm {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)$
for the
$\mathrm {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)$
for the
![]() ${\hbar }$
-adic completion of
${\hbar }$
-adic completion of
![]() $ {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)$
. This is a
$ {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)$
. This is a
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra contained in the formal series space
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra contained in the formal series space
![]() $(Y_{\hbar }\mathfrak {g}\otimes Y_{\hbar }\mathfrak {g})[\kern-1.2pt\![z^{\pm 1}]\!\kern-1.2pt]$
(see Lemma 4.5). As in (4.2), evaluation at
$(Y_{\hbar }\mathfrak {g}\otimes Y_{\hbar }\mathfrak {g})[\kern-1.2pt\![z^{\pm 1}]\!\kern-1.2pt]$
(see Lemma 4.5). As in (4.2), evaluation at
![]() $z=1$
yields a
$z=1$
yields a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra epimorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra epimorphism
Next, let ![]() denote the natural
denote the natural
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
given by evaluating
![]() $w\mapsto z$
. Then, since
$w\mapsto z$
. Then, since ![]() is a
is a
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism ![]() and
and
![]() $\Delta $
is homogeneous of degree zero, the first relation of Part (1) in Proposition 7.1 is equivalent to the identity
$\Delta $
is homogeneous of degree zero, the first relation of Part (1) in Proposition 7.1 is equivalent to the identity
in ![]() . As
. As ![]() satisfies the relation
satisfies the relation ![]() , applying
, applying
![]() $\mathscr{E}\mathscr{v}^{\scriptscriptstyle {(2)}}$
to the above identity recovers
$\mathscr{E}\mathscr{v}^{\scriptscriptstyle {(2)}}$
to the above identity recovers ![]() .
.
7.2
 $\mathrm {D}Y_{\hbar }\mathfrak {g}$
as a quantization
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
as a quantization
With Proposition 7.1 and Corollary 7.3 in hand, we now turn to proving that
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
provides a homogeneous quantization of the
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
provides a homogeneous quantization of the
![]() $\mathbb {Z}$
-graded Lie bialgebra
$\mathbb {Z}$
-graded Lie bialgebra
![]() $\mathfrak {t}=\mathfrak {g}[t^{\pm 1}]$
, equipped with the Lie cobracket
$\mathfrak {t}=\mathfrak {g}[t^{\pm 1}]$
, equipped with the Lie cobracket
![]() $\delta $
defined in Section 2.5.
$\delta $
defined in Section 2.5.
To begin, observe that the homomorphisms ![]() and
and ![]() satisfy the relation
satisfy the relation
where
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Gamma _z$
are as in Theorem 4.8 and (4.3), respectively. The
$\Gamma _z$
are as in Theorem 4.8 and (4.3), respectively. The
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism defined by either side of this relation shall be denoted
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism defined by either side of this relation shall be denoted
![]() $\check {\imath }$
:
$\check {\imath }$
:
The following lemma shows that
![]() $\check {\imath }$
is injective,
$\check {\imath }$
is injective,
![]() $\mathbb {Z}$
-graded, and has image contained in the Yangian double
$\mathbb {Z}$
-graded, and has image contained in the Yangian double
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
.
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
.
Lemma 7.4 The morphism
![]() $\check {\imath }$
is an embedding of
$\check {\imath }$
is an embedding of
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras
satisfying ![]() and
and ![]() . In particular,
. In particular, ![]() and
and ![]() are both injective.
are both injective.
Proof Since
![]() $\Gamma _z\circ \Phi _z=\mathbf {1}_{\mathrm {D}Y_{\hbar }\mathfrak {g}}$
, Part (4) of Proposition 7.1 yields
$\Gamma _z\circ \Phi _z=\mathbf {1}_{\mathrm {D}Y_{\hbar }\mathfrak {g}}$
, Part (4) of Proposition 7.1 yields
 $$ \begin{align} \begin{gathered} \check{\imath}\,({\mathsf{X}}_\beta^\pm(u))=\Gamma_z(\Phi_z({\dot{x}}_\beta^\pm(u)))={\dot{x}}_\beta^\pm(u)\quad \forall\; \beta\in \Delta^+,\\ \check{\imath}\,({\mathsf{h}}_i(u))=\Gamma_z(\Phi_z(\dot{h}_i(u)))=\dot{h}_i(u)\quad \forall\; i \in \mathbf{I}. \end{gathered} \end{align} $$
$$ \begin{align} \begin{gathered} \check{\imath}\,({\mathsf{X}}_\beta^\pm(u))=\Gamma_z(\Phi_z({\dot{x}}_\beta^\pm(u)))={\dot{x}}_\beta^\pm(u)\quad \forall\; \beta\in \Delta^+,\\ \check{\imath}\,({\mathsf{h}}_i(u))=\Gamma_z(\Phi_z(\dot{h}_i(u)))=\dot{h}_i(u)\quad \forall\; i \in \mathbf{I}. \end{gathered} \end{align} $$
By Remark 4.9,
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a closed subspace of its
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a closed subspace of its
![]() $\mathcal {J}$
-adic completion, viewed as a topological
$\mathcal {J}$
-adic completion, viewed as a topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module. As
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module. As ![]() is topologically generated as a
is topologically generated as a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra by the coefficients of all the series
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra by the coefficients of all the series
![]() ${\mathsf {X}}_\beta ^\pm (u)$
and
${\mathsf {X}}_\beta ^\pm (u)$
and
![]() ${\mathsf {h}}_i(u)$
(by Lemma 6.8), the equalities (7.2) imply that
${\mathsf {h}}_i(u)$
(by Lemma 6.8), the equalities (7.2) imply that
![]() $\check {\imath }$
has image in
$\check {\imath }$
has image in
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
and thus can be viewed as a
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
and thus can be viewed as a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
which necessarily satisfies ![]() . Similarly, since
. Similarly, since
![]() $\Phi _z(\mathrm {D}Y_{\hbar }\mathfrak {g})$
is closed in
$\Phi _z(\mathrm {D}Y_{\hbar }\mathfrak {g})$
is closed in
![]() $\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
(see Remark 4.9), Part (4) of Proposition 7.1 and (7.2) give
$\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
(see Remark 4.9), Part (4) of Proposition 7.1 and (7.2) give ![]() .
.
As ![]() and
and
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
are both topologically free, it follows from Lemma 2.1 that
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
are both topologically free, it follows from Lemma 2.1 that
![]() $\check {\imath }$
will be injective provided its semiclassical limit
$\check {\imath }$
will be injective provided its semiclassical limit
![]() $\check {\underline {\imath }}: U({\mathfrak {t}}_{\scriptscriptstyle {-}})\to U(\mathfrak {t})$
is. That this is indeed the case is a consequence of Lemma 6.8, the relations (7.2), and the definitions of
$\check {\underline {\imath }}: U({\mathfrak {t}}_{\scriptscriptstyle {-}})\to U(\mathfrak {t})$
is. That this is indeed the case is a consequence of Lemma 6.8, the relations (7.2), and the definitions of
![]() ${\dot {x}}_\beta ^\pm (u)$
and
${\dot {x}}_\beta ^\pm (u)$
and
![]() $\dot {h}_i(u)$
given in Section 4.2, which imply that
$\dot {h}_i(u)$
given in Section 4.2, which imply that
![]() $\check {\underline {\imath }}$
coincides with the natural inclusion of
$\check {\underline {\imath }}$
coincides with the natural inclusion of
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
into
$U({\mathfrak {t}}_{\scriptscriptstyle {-}})$
into
![]() $U(\mathfrak {t})$
induced by the polarization
$U(\mathfrak {t})$
induced by the polarization ![]() .
.
Finally, by Part (2) of Theorem 4.6 and Part (3) of Proposition 7.1,
![]() $\Phi _z$
and
$\Phi _z$
and ![]() are both
are both
![]() $\mathbb {Z}$
-graded (see Remarks 4.7 and 7.2). As
$\mathbb {Z}$
-graded (see Remarks 4.7 and 7.2). As
![]() $\Phi _z$
is injective, it follows automatically that
$\Phi _z$
is injective, it follows automatically that
![]() $\check {\imath }$
is
$\check {\imath }$
is
![]() $\mathbb {Z}$
-graded.
$\mathbb {Z}$
-graded.
The embedding
![]() $\check {\imath }$
is at the heart of the following theorem, which provides the first main result of this article.
$\check {\imath }$
is at the heart of the following theorem, which provides the first main result of this article.
Theorem 7.5 There is a unique
![]() $\mathbb {Z}$
-graded topological Hopf algebra structure on
$\mathbb {Z}$
-graded topological Hopf algebra structure on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
such that the inclusions
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
such that the inclusions
are morphisms of
![]() $\mathbb {Z}$
-graded topological Hopf algebras over
$\mathbb {Z}$
-graded topological Hopf algebras over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. Equipped with this Hopf structure,
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. Equipped with this Hopf structure,
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a homogeneous quantization of the Lie bialgebra
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a homogeneous quantization of the Lie bialgebra
![]() $(\mathfrak {t} ,\delta )$
.
$(\mathfrak {t} ,\delta )$
.
Proof If
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
can be equipped with a coproduct
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
can be equipped with a coproduct
![]() $\dot \Delta $
, counit
$\dot \Delta $
, counit
![]() $\dot \varepsilon $
, and antipode
$\dot \varepsilon $
, and antipode
![]() $\dot S$
which give it the structure of a topological Hopf algebra over
$\dot S$
which give it the structure of a topological Hopf algebra over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
and, in addition, make
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
and, in addition, make
![]() $\imath $
and
$\imath $
and
![]() $\check {\imath }$
morphisms of
$\check {\imath }$
morphisms of
![]() $\mathbb {Z}$
-graded topological Hopf algebras, then this structure is necessarily unique and
$\mathbb {Z}$
-graded topological Hopf algebras, then this structure is necessarily unique and
![]() $\mathbb {Z}$
-graded. Indeed,
$\mathbb {Z}$
-graded. Indeed,
![]() $\dot \Delta $
,
$\dot \Delta $
,
![]() $\dot \varepsilon $
, and
$\dot \varepsilon $
, and
![]() $\dot S$
are determined by their values on any set of generators of the topological algebra
$\dot S$
are determined by their values on any set of generators of the topological algebra
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
, and thus by their values on
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
, and thus by their values on ![]() .
.
Let us now establish the existence of a topological Hopf structure on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
over
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
with the claimed properties. We begin by observing that
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
with the claimed properties. We begin by observing that
![]() $\imath $
and
$\imath $
and
![]() $\check {\imath }$
satisfy the relations
$\check {\imath }$
satisfy the relations

The first relation follows from the identity
![]() $\Phi \circ \imath =\tau _1$
and that, for each
$\Phi \circ \imath =\tau _1$
and that, for each
![]() $c\in \mathbb {C}$
,
$c\in \mathbb {C}$
,
![]() $\tau _c$
is a Hopf algebra automorphism (see Section 3.3). As for the second relation, since
$\tau _c$
is a Hopf algebra automorphism (see Section 3.3). As for the second relation, since ![]() , Corollary 7.3 yields
, Corollary 7.3 yields
Since
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a generated as a topological
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a generated as a topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra by
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra by ![]() , these relations imply that
, these relations imply that
![]() $\Delta \circ \Phi $
has image satisfying
$\Delta \circ \Phi $
has image satisfying
where we view the right-hand side as subspace of
![]() $\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {)}}^{\scriptscriptstyle (2)}$
, as in Corollary 7.3. We may therefore introduce a
$\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {)}}^{\scriptscriptstyle (2)}$
, as in Corollary 7.3. We may therefore introduce a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
![]() $\dot \Delta $
by
$\dot \Delta $
by
where
![]() $\Gamma $
is the inverse of
$\Gamma $
is the inverse of
![]() $\widehat {\Phi }$
, as in Theorem 4.8. Since
$\widehat {\Phi }$
, as in Theorem 4.8. Since
![]() $\Gamma \circ \Phi =\mathbf {1}$
, it follows from this definition and the relations (7.3) that
$\Gamma \circ \Phi =\mathbf {1}$
, it follows from this definition and the relations (7.3) that
Similarly, from Corollary 7.3 and the relations
![]() $\tau _1\circ S=S\circ \tau _1$
and
$\tau _1\circ S=S\circ \tau _1$
and
![]() $\varepsilon \circ \tau _1=\varepsilon $
, we find that
$\varepsilon \circ \tau _1=\varepsilon $
, we find that
![]() $\imath $
and
$\imath $
and
![]() $\check {\imath }$
satisfy
$\check {\imath }$
satisfy

In particular, these relations imply that
![]() $\mathrm {Im}(S\circ \Phi )\subset \mathrm {Im}(\Phi )$
. We may therefore define morphisms
$\mathrm {Im}(S\circ \Phi )\subset \mathrm {Im}(\Phi )$
. We may therefore define morphisms
![]() $\dot {S}$
and
$\dot {S}$
and
![]() $\dot {\varepsilon }$
by
$\dot {\varepsilon }$
by
which by construction satisfy the compatibility relations
Since
![]() $\Gamma |_{\mathrm {Im}(\Phi )}=\Phi ^{-1}$
and
$\Gamma |_{\mathrm {Im}(\Phi )}=\Phi ^{-1}$
and
![]() $Y_{\hbar }\mathfrak {g}$
is a topological Hopf algebra with coproduct
$Y_{\hbar }\mathfrak {g}$
is a topological Hopf algebra with coproduct
![]() $\Delta $
, antipode S, and counit
$\Delta $
, antipode S, and counit
![]() $\varepsilon $
, the above definitions imply that
$\varepsilon $
, the above definitions imply that
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a topological Hopf algebra over
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a topological Hopf algebra over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
with coproduct
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
with coproduct
![]() $\dot \Delta $
, antipode
$\dot \Delta $
, antipode
![]() $\dot S$
, and counit
$\dot S$
, and counit
![]() $\dot \varepsilon $
. Moreover, the relations (7.4) and (7.5) prove that, when
$\dot \varepsilon $
. Moreover, the relations (7.4) and (7.5) prove that, when
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is given this Hopf structure, the
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is given this Hopf structure, the
![]() $\mathbb {Z}$
-graded embeddings
$\mathbb {Z}$
-graded embeddings
![]() $\imath $
and
$\imath $
and
![]() $\check {\imath }$
are homomorphisms of topological Hopf algebras.
$\check {\imath }$
are homomorphisms of topological Hopf algebras.
We are left to establish the second assertion of the theorem. By what we have shown so far and Theorem 4.3,
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a flat,
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a flat,
![]() $\mathbb {Z}$
-graded Hopf algebra deformation of the universal enveloping
$\mathbb {Z}$
-graded Hopf algebra deformation of the universal enveloping
![]() $U(\mathfrak {t})$
of
$U(\mathfrak {t})$
of
![]() $\mathfrak {t}=\mathfrak {g}[t^{\pm 1}]$
over
$\mathfrak {t}=\mathfrak {g}[t^{\pm 1}]$
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. It thus provides a homogeneous quantization of a
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. It thus provides a homogeneous quantization of a
![]() $\mathbb {Z}$
-graded Lie bialgebra structure on the Lie algebra
$\mathbb {Z}$
-graded Lie bialgebra structure on the Lie algebra
![]() $\mathfrak {t}$
with cobracket
$\mathfrak {t}$
with cobracket
![]() $\delta _{\mathfrak {t}}$
given by the formula (2.2). From Theorems 6.7 and 6.7 and the first part of the theorem,
$\delta _{\mathfrak {t}}$
given by the formula (2.2). From Theorems 6.7 and 6.7 and the first part of the theorem,
![]() $\delta _{\mathfrak {t}}$
satisfies
$\delta _{\mathfrak {t}}$
satisfies
![]() $\delta _{\mathfrak {t}}|_{{\mathfrak {t}}_{\scriptscriptstyle {+}}}=\delta _{\scriptscriptstyle +}$
and
$\delta _{\mathfrak {t}}|_{{\mathfrak {t}}_{\scriptscriptstyle {+}}}=\delta _{\scriptscriptstyle +}$
and
![]() $\delta _{\mathfrak {t}}|_{{\mathfrak {t}}_{\scriptscriptstyle {-}}}=-\delta _{\scriptscriptstyle -}$
. As
$\delta _{\mathfrak {t}}|_{{\mathfrak {t}}_{\scriptscriptstyle {-}}}=-\delta _{\scriptscriptstyle -}$
. As ![]() , we can conclude that
, we can conclude that
![]() $\delta _{\mathfrak {t}}$
coincides with the Lie cobracket
$\delta _{\mathfrak {t}}$
coincides with the Lie cobracket
![]() $\delta $
defined in Section 2.5.
$\delta $
defined in Section 2.5.
Remark 7.6 The proof of Theorem 7.5 shows that the coproduct
![]() $\dot \Delta $
, counit
$\dot \Delta $
, counit
![]() $\dot \varepsilon $
, and antipode
$\dot \varepsilon $
, and antipode
![]() $\dot S$
on
$\dot S$
on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
are uniquely determined by the requirement that
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
are uniquely determined by the requirement that
![]() $\Phi $
is a homomorphism of topological Hopf algebras
$\Phi $
is a homomorphism of topological Hopf algebras
where
![]() $\widehat {Y_{\hbar }\mathfrak {g}}$
is given the topological Hopf structure defined above Corollary 7.3. Here, we emphasize that although
$\widehat {Y_{\hbar }\mathfrak {g}}$
is given the topological Hopf structure defined above Corollary 7.3. Here, we emphasize that although
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a genuine topological Hopf algebra over
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a genuine topological Hopf algebra over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
in the sense of Section 2.1, the completed Yangian
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
in the sense of Section 2.1, the completed Yangian
![]() $\widehat {Y_{\hbar }\mathfrak {g}}$
is not. In the same breath, the Hopf algebra structure on
$\widehat {Y_{\hbar }\mathfrak {g}}$
is not. In the same breath, the Hopf algebra structure on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is uniquely characterized by the requirement that
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is uniquely characterized by the requirement that
![]() $\Phi _z$
satisfies the relations
$\Phi _z$
satisfies the relations
where ![]() is as in the proof of Corollary 7.3. In particular, this makes precise the uniqueness statement in the first assertion of Theorem I.
is as in the proof of Corollary 7.3. In particular, this makes precise the uniqueness statement in the first assertion of Theorem I.
7.3 The dual triangular decomposition revisited
We conclude this section by giving an equivalent characterization of the restricted dual
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
to
${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
to
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}$
considered in Section 6.5, where we recall that
${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}$
considered in Section 6.5, where we recall that
![]() $\chi $
takes value
$\chi $
takes value
![]() $+$
,
$+$
,
![]() $-$
or
$-$
or
![]() $0$
.
$0$
.
Corollary 7.7 For each choice of
![]() $\chi $
,
$\chi $
,
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
satisfies
${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
satisfies
Proof From the definitions of
![]() ${\dot {\mathsf {Y}}}_{\hbar }^\chi \mathfrak {g}$
and
${\dot {\mathsf {Y}}}_{\hbar }^\chi \mathfrak {g}$
and ![]() , and the Gauss decomposition of the universal R-matrix, we obtain the sequence of inclusions
, and the Gauss decomposition of the universal R-matrix, we obtain the sequence of inclusions
It therefore suffices to show that ![]() . We shall establish this for
. We shall establish this for
![]() $\chi =-$
. The proof in the remaining cases is identical, and hence omitted.
$\chi =-$
. The proof in the remaining cases is identical, and hence omitted.
Let
![]() $\pi _+:Y_{\hbar }\mathfrak {g}\to Y_{\hbar }^{+\!}\mathfrak {g}$
be the
$\pi _+:Y_{\hbar }\mathfrak {g}\to Y_{\hbar }^{+\!}\mathfrak {g}$
be the
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear projection associated with the opposite triangular decomposition
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear projection associated with the opposite triangular decomposition
![]() $Y_{\hbar }\mathfrak {g}\cong Y_{\hbar }^{-\!}\mathfrak {g}\otimes Y_{\hbar }^0\mathfrak {g}\otimes Y_{\hbar }^{+\!}\mathfrak {g}$
from Remark 3.7, and suppose
$Y_{\hbar }\mathfrak {g}\cong Y_{\hbar }^{-\!}\mathfrak {g}\otimes Y_{\hbar }^0\mathfrak {g}\otimes Y_{\hbar }^{+\!}\mathfrak {g}$
from Remark 3.7, and suppose
![]() $f\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
satisfies
$f\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
satisfies
![]() $\Phi _z(f)\in Y_{\hbar }^{+}\!\mathfrak {g} [\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. We wish to show that
$\Phi _z(f)\in Y_{\hbar }^{+}\!\mathfrak {g} [\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. We wish to show that
![]() $f\in {\dot {\mathsf {Y}}}_{\hbar }^{-\!}\mathfrak {g}{\vphantom {)}}^\star $
.
$f\in {\dot {\mathsf {Y}}}_{\hbar }^{-\!}\mathfrak {g}{\vphantom {)}}^\star $
.
To begin, note that since
![]() $(\mathbf {1}\otimes \varepsilon )\mathcal {R}^\chi (z)=1$
, we have
$(\mathbf {1}\otimes \varepsilon )\mathcal {R}^\chi (z)=1$
, we have
Consider now the element
![]() $f\circ \pi ^-\in {\dot {\mathsf {Y}}}_{\hbar }^{-}\mathfrak {g}{\vphantom {)}}^\star \subset {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
, where
$f\circ \pi ^-\in {\dot {\mathsf {Y}}}_{\hbar }^{-}\mathfrak {g}{\vphantom {)}}^\star \subset {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
, where
![]() $\pi ^-:{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\to {\dot {\mathsf {Y}}}_{\hbar }^{-}\mathfrak {g}$
is as in Section 6.5. Since
$\pi ^-:{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\to {\dot {\mathsf {Y}}}_{\hbar }^{-}\mathfrak {g}$
is as in Section 6.5. Since
![]() $(\pi ^-\otimes \mathbf {1})\mathcal {R}(z)=\mathcal {R}^-(z)$
, it satisfies
$(\pi ^-\otimes \mathbf {1})\mathcal {R}(z)=\mathcal {R}^-(z)$
, it satisfies
As ![]() is injective (by Lemma 7.4), we can conclude that
is injective (by Lemma 7.4), we can conclude that
![]() $f=f\circ \pi ^-\in {\dot {\mathsf {Y}}}_{\hbar }^{-}\mathfrak {g}{\vphantom {)}}^\star $
.
$f=f\circ \pi ^-\in {\dot {\mathsf {Y}}}_{\hbar }^{-}\mathfrak {g}{\vphantom {)}}^\star $
.
Remark 7.8 Since
![]() $Y_{\hbar }^{\pm \!}\mathfrak {g}$
and
$Y_{\hbar }^{\pm \!}\mathfrak {g}$
and
![]() $Y_{\hbar }^0\mathfrak {g}$
are
$Y_{\hbar }^0\mathfrak {g}$
are
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-subalgebras of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-subalgebras of
![]() $Y_{\hbar }\mathfrak {g}$
, it follows from this corollary that
$Y_{\hbar }\mathfrak {g}$
, it follows from this corollary that
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
is a
${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
is a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-subalgebra of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-subalgebra of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
for each choice of
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
for each choice of
![]() $\chi $
. In addition, it is immediate from this characterization and Part (4) of Proposition 7.1 that the coefficients of the series
$\chi $
. In addition, it is immediate from this characterization and Part (4) of Proposition 7.1 that the coefficients of the series
![]() ${\mathsf {X}}_\beta ^\pm (u)$
and
${\mathsf {X}}_\beta ^\pm (u)$
and
![]() ${\mathsf {h}}_i(u)$
belong to
${\mathsf {h}}_i(u)$
belong to
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\mp }\mathfrak {g}{\vphantom {)}}^\star $
and
${\dot {\mathsf {Y}}}_{\hbar }^{\mp }\mathfrak {g}{\vphantom {)}}^\star $
and
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
, respectively, for each
${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
, respectively, for each
![]() $\beta \in \Delta ^+$
and
$\beta \in \Delta ^+$
and
![]() $i\in \mathbf {I}$
. Similarly, since
$i\in \mathbf {I}$
. Similarly, since ![]() is injective and
is injective and
![]() $Y_{\hbar }^0\mathfrak {g}$
is commutative, we deduce that
$Y_{\hbar }^0\mathfrak {g}$
is commutative, we deduce that
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
is commutative.
${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
is commutative.
In particular, these observations complete the proof of Proposition 6.9. We emphasize that we have not applied that proposition in establishing any of the results in Section 7.
8
 $\mathrm {D}Y_{\hbar }\mathfrak {g}$
as a quantum double
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
as a quantum double
We now turn to reframing Theorem 7.5 in the context of the quantum double. Our central objective is to prove the second main result of this article, Theorem 8.4, which establishes that the Yangian double
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is isomorphic, as a
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is isomorphic, as a
![]() $\mathbb {Z}$
-graded topological Hopf algebra over
$\mathbb {Z}$
-graded topological Hopf algebra over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, to the restricted quantum double of the Yangian, which is defined explicitly in Section 8.2.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, to the restricted quantum double of the Yangian, which is defined explicitly in Section 8.2.
8.1 The quantum double of
 $U_{\hbar }\mathfrak {b}$
$U_{\hbar }\mathfrak {b}$
Let us begin by recalling, in broad strokes, the general construction of the quantum double of a quantized enveloping algebra, as was first outlined by Drinfeld in [Reference Drinfel’d7, Section 13].
Suppose that
![]() $U_{\hbar }\mathfrak {b}$
is a quantization of a finite-dimensional Lie bialgebra
$U_{\hbar }\mathfrak {b}$
is a quantization of a finite-dimensional Lie bialgebra
![]() $\mathfrak {b}$
, and let
$\mathfrak {b}$
, and let ![]() denote the quantized enveloping algebra
denote the quantized enveloping algebra
![]() $(U_{\hbar }{\mathfrak {b}}^{\circ }){\vphantom {)}}^{\scriptscriptstyle \mathrm {cop}}$
, where
$(U_{\hbar }{\mathfrak {b}}^{\circ }){\vphantom {)}}^{\scriptscriptstyle \mathrm {cop}}$
, where
![]() $U_{\hbar }{\mathfrak {b}}^{\circ }$
is the topological dual to
$U_{\hbar }{\mathfrak {b}}^{\circ }$
is the topological dual to
![]() $U_{\hbar }{\mathfrak {b}}^\prime $
introduced in Section 5.1. Then there exists a unique topological Hopf algebra
$U_{\hbar }{\mathfrak {b}}^\prime $
introduced in Section 5.1. Then there exists a unique topological Hopf algebra
![]() $D(U_{\hbar }\mathfrak {b})$
over
$D(U_{\hbar }\mathfrak {b})$
over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, the quantum double of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, the quantum double of
![]() $U_{\hbar }\mathfrak {b}$
, satisfying the following three properties:
$U_{\hbar }\mathfrak {b}$
, satisfying the following three properties:
-
(1) There are embeddings of topological Hopf algebras

-
(2) The composite
 is an isomorphism of
is an isomorphism of
 $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules. -
(3) The canonical element
 associated with the pairing between
associated with the pairing between
 $U_{\hbar }{\mathfrak {b}}^\prime $
and
$U_{\hbar }{\mathfrak {b}}^\prime $
and
 $U_{\hbar }{\mathfrak {b}}^\circ $
, which coincides with the canonical tensor in
$U_{\hbar }{\mathfrak {b}}^\circ $
, which coincides with the canonical tensor in
 $U_{\hbar }\mathfrak {b}\otimes U_{\hbar }{\mathfrak {b}}^\ast $
, defines a quasitriangular structure on
$U_{\hbar }\mathfrak {b}\otimes U_{\hbar }{\mathfrak {b}}^\ast $
, defines a quasitriangular structure on
 $D(U_{\hbar }\mathfrak {b})$
. That is, one has
$D(U_{\hbar }\mathfrak {b})$
. That is, one has 
In addition,
![]() $D(U_{\hbar }\mathfrak {b})$
provides a quantization of the Drinfeld double of the finite-dimensional Lie bialgebra
$D(U_{\hbar }\mathfrak {b})$
provides a quantization of the Drinfeld double of the finite-dimensional Lie bialgebra
![]() $\mathfrak {b}$
.
$\mathfrak {b}$
.
The quantum double
![]() $D(U_{\hbar }\mathfrak {b})$
can be realized explicitly as the tensor product of topological coalgebras
$D(U_{\hbar }\mathfrak {b})$
can be realized explicitly as the tensor product of topological coalgebras ![]() , with multiplication determined from the cross relations
, with multiplication determined from the cross relations
where we have used the sumless Sweedler notation for iterated coproducts on
![]() $U_{\hbar }\mathfrak {b}$
and
$U_{\hbar }\mathfrak {b}$
and ![]() , and
, and
![]() $\imath $
and
$\imath $
and
![]() $\check {\imath }$
are now given by
$\check {\imath }$
are now given by
![]() $\imath (x)=1\otimes x$
and
$\imath (x)=1\otimes x$
and
![]() $\check {\imath }(f)=f\otimes 1$
for all
$\check {\imath }(f)=f\otimes 1$
for all
![]() $x\in U_{\hbar }\mathfrak {b}$
and
$x\in U_{\hbar }\mathfrak {b}$
and ![]() . As spelled out in detail in [Reference Appel and Toledano Laredo1, Section A.5], this can be realized as a special instance of the double cross-product construction. Namely, one has
. As spelled out in detail in [Reference Appel and Toledano Laredo1, Section A.5], this can be realized as a special instance of the double cross-product construction. Namely, one has
with respect to the left coadjoint action
![]() $\rhd $
of
$\rhd $
of
![]() $U_{\hbar }\mathfrak {b}$
on
$U_{\hbar }\mathfrak {b}$
on ![]() and the right coadjoint action
and the right coadjoint action
![]() $\lhd $
on
$\lhd $
on ![]() on
on
![]() $U_{\hbar }\mathfrak {b}$
. Given the
$U_{\hbar }\mathfrak {b}$
. Given the
![]() $U_{\hbar }\mathfrak {b}$
analogue of Lemma 5.8, established in [Reference Appel and Toledano Laredo1, Proposition A.5], this construction of
$U_{\hbar }\mathfrak {b}$
analogue of Lemma 5.8, established in [Reference Appel and Toledano Laredo1, Proposition A.5], this construction of
![]() $D(U_{\hbar }\mathfrak {b})$
proceeds identically to the analogous construction for the quantum double of a finite-dimensional Hopf algebra; we refer the reader to the texts [Reference Majid36, Section 7], [Reference Kassel26, Section IX.4], [Reference Klimyk and Schmüdgen33, Section 8.2] and [Reference Montgomery37, Section 10.3], for instance, as well as the articles [Reference Majid34, Reference Majid35, Reference Radford39].
$D(U_{\hbar }\mathfrak {b})$
proceeds identically to the analogous construction for the quantum double of a finite-dimensional Hopf algebra; we refer the reader to the texts [Reference Majid36, Section 7], [Reference Kassel26, Section IX.4], [Reference Klimyk and Schmüdgen33, Section 8.2] and [Reference Montgomery37, Section 10.3], for instance, as well as the articles [Reference Majid34, Reference Majid35, Reference Radford39].
8.2 The restricted quantum double of the Yangian
In our case,
![]() $U_{\hbar }\mathfrak {b}=Y_{\hbar }\mathfrak {g}$
is not a quantization of a finite-dimensional Lie bialgebra, but rather a homogeneous quantization of an
$U_{\hbar }\mathfrak {b}=Y_{\hbar }\mathfrak {g}$
is not a quantization of a finite-dimensional Lie bialgebra, but rather a homogeneous quantization of an
![]() $\mathbb {N}$
-graded Lie bialgebra
$\mathbb {N}$
-graded Lie bialgebra
![]() $\mathfrak {b}$
with finite-dimensional graded components
$\mathfrak {b}$
with finite-dimensional graded components
![]() $\mathfrak {b}_k$
. In this setting, the double cross-product construction alluded to above remains valid provided all duals are taken in the category of
$\mathfrak {b}_k$
. In this setting, the double cross-product construction alluded to above remains valid provided all duals are taken in the category of
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules; that is, we replace
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules; that is, we replace ![]() with
with ![]() . This produces the restricted quantum double
. This produces the restricted quantum double
![]() $D(U_{\hbar }\mathfrak {b})$
of
$D(U_{\hbar }\mathfrak {b})$
of
![]() $U_{\hbar }\mathfrak {b}$
.
$U_{\hbar }\mathfrak {b}$
.
Let us now give the detailed construction of this topological Hopf algebra. Following Section 5.4, let
![]() $\blacktriangledown $
and
$\blacktriangledown $
and
![]() $\blacktriangle $
denote the left adjoint action of
$\blacktriangle $
denote the left adjoint action of
![]() $Y_{\hbar }\mathfrak {g}$
on itself, and the right adjoint coaction of
$Y_{\hbar }\mathfrak {g}$
on itself, and the right adjoint coaction of
![]() $Y_{\hbar }\mathfrak {g}$
on itself, respectively:
$Y_{\hbar }\mathfrak {g}$
on itself, respectively:
 $$ \begin{gather*} \blacktriangledown= m^3\circ (\mathbf{1}^{\otimes 2}\otimes S)\circ (2\,3)\circ (\Delta \otimes \mathbf{1}), \\ \blacktriangle=(1\otimes m)\circ (1\,2)\circ (S\otimes \mathbf{1}^{\otimes 2})\circ \Delta^3, \end{gather*} $$
$$ \begin{gather*} \blacktriangledown= m^3\circ (\mathbf{1}^{\otimes 2}\otimes S)\circ (2\,3)\circ (\Delta \otimes \mathbf{1}), \\ \blacktriangle=(1\otimes m)\circ (1\,2)\circ (S\otimes \mathbf{1}^{\otimes 2})\circ \Delta^3, \end{gather*} $$
where all tensor products are now taken to be the topological tensor product over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. By Lemma 5.8, we have
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. By Lemma 5.8, we have
We may thus dualize
![]() $\blacktriangledown $
and
$\blacktriangledown $
and
![]() $\blacktriangle $
to obtain the so-called left and right coadjoint actions
$\blacktriangle $
to obtain the so-called left and right coadjoint actions
respectively, of
![]() $Y_{\hbar }\mathfrak {g}$
on
$Y_{\hbar }\mathfrak {g}$
on ![]() and of
and of ![]() on
on
![]() $Y_{\hbar }\mathfrak {g}$
. These are defined on simple tensors by the formulas
$Y_{\hbar }\mathfrak {g}$
. These are defined on simple tensors by the formulas
for all
![]() $x\in Y_{\hbar }\mathfrak {g}$
,
$x\in Y_{\hbar }\mathfrak {g}$
, ![]() , and
, and
![]() $y\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
, where the action of
$y\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
, where the action of
![]() $S^{-1}(x)$
on y is given by
$S^{-1}(x)$
on y is given by
![]() $\blacktriangledown $
and we have written
$\blacktriangledown $
and we have written
![]() $x \vartriangleright \!f$
for
$x \vartriangleright \!f$
for
![]() $\vartriangleright \!(x\otimes f)$
and
$\vartriangleright \!(x\otimes f)$
and
![]() $x\vartriangleleft f$
for
$x\vartriangleleft f$
for
![]() $\vartriangleleft \!(x\otimes f)$
.
$\vartriangleleft \!(x\otimes f)$
.
The tuple ![]() forms a matched pair of
forms a matched pair of
![]() $\mathbb {Z}$
-graded topological Hopf algebras over
$\mathbb {Z}$
-graded topological Hopf algebras over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. Explicitly,
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. Explicitly,
![]() $\rhd $
and
$\rhd $
and
![]() $\lhd $
are
$\lhd $
are
![]() $\mathbb {Z}$
-graded homomorphisms of topological
$\mathbb {Z}$
-graded homomorphisms of topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules which satisfy the following set of conditions:
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules which satisfy the following set of conditions:
-
(M1)
 is a left
is a left
 $Y_{\hbar }\mathfrak {g}$
-module coalgebra and
$Y_{\hbar }\mathfrak {g}$
-module coalgebra and
 $(Y_{\hbar }\mathfrak {g},\lhd )$
is a right
$(Y_{\hbar }\mathfrak {g},\lhd )$
is a right  -module coalgebra. Equivalently,
-module coalgebra. Equivalently,
 $\rhd $
and
$\rhd $
and
 $\lhd $
are morphisms of topological coalgebras: which make
$\lhd $
are morphisms of topological coalgebras: which make
 a left
a left
 $Y_{\hbar }\mathfrak {g}$
-module and
$Y_{\hbar }\mathfrak {g}$
-module and
 $Y_{\hbar }\mathfrak {g}$
a right
$Y_{\hbar }\mathfrak {g}$
a right  -module.
-module.
-
(M2)
 $\lhd $
and
$\lhd $
and
 $\rhd $
are compatible with the products m and
$\rhd $
are compatible with the products m and  on
on
 $Y_{\hbar }\mathfrak {g}$
and
$Y_{\hbar }\mathfrak {g}$
and  :
: 
-
(M3) The unit maps
 $\iota $
and
$\iota $
and  are module homomorphisms:
are module homomorphisms: 
-
(M4)
 $\lhd $
and
$\lhd $
and
 $\rhd $
satisfy the compatibility relation
$\rhd $
satisfy the compatibility relation 
Here, we note that the above conditions coincide with those from [Reference Kassel26, Definition IX.2.2], [Reference Radford39, Section 2], and [Reference Appel and Toledano Laredo1, Section A.1], which agree with those from [Reference Majid36, Definition 7.2.1] up to conventions on the order in which the tensor factors appear.
Since ![]() and
and
![]() $Y_{\hbar }\mathfrak {g}$
are matched, we may form the double cross-product Hopf algebra
$Y_{\hbar }\mathfrak {g}$
are matched, we may form the double cross-product Hopf algebra ![]() in the category of
in the category of
![]() $\mathbb {Z}$
-graded topological Hopf algebras over
$\mathbb {Z}$
-graded topological Hopf algebras over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
by following the standard procedure (see [Reference Kassel26, Theorem IX.2.3] or [Reference Majid36, Theorem 7.2.2], for instance). As a
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
by following the standard procedure (see [Reference Kassel26, Theorem IX.2.3] or [Reference Majid36, Theorem 7.2.2], for instance). As a
![]() $\mathbb {Z}$
-graded topological coalgebra,
$\mathbb {Z}$
-graded topological coalgebra, ![]() coincides with the tensor product of
coincides with the tensor product of ![]() and
and
![]() $Y_{\hbar }\mathfrak {g}$
:
$Y_{\hbar }\mathfrak {g}$
:

where
![]() $\Delta _D$
denotes the coproduct and
$\Delta _D$
denotes the coproduct and
![]() $\varepsilon _D$
denotes the counit. The algebra structure on
$\varepsilon _D$
denotes the counit. The algebra structure on ![]() is uniquely determined by the requirement that the inclusions
is uniquely determined by the requirement that the inclusions
are
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphisms satisfying the relations
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphisms satisfying the relations

where
![]() $m_D$
denotes the multiplication on
$m_D$
denotes the multiplication on
![]() $D(Y_{\hbar }\mathfrak {g})$
. In particular, the unit map is
$D(Y_{\hbar }\mathfrak {g})$
. In particular, the unit map is ![]() . Finally, the antipode
. Finally, the antipode
![]() $S_D$
on
$S_D$
on ![]() is given by
is given by
This double cross-product Hopf algebra is the restricted quantum double of the Yangian, as we formally record in the below definition.
Definition 8.1 The
![]() $\mathbb {Z}$
-graded topological Hopf algebra
$\mathbb {Z}$
-graded topological Hopf algebra ![]() is called the restricted quantum double of the Yangian
is called the restricted quantum double of the Yangian
![]() $Y_{\hbar }\mathfrak {g}$
, and is denoted
$Y_{\hbar }\mathfrak {g}$
, and is denoted
This definition, together with the general theory, implies that
![]() $D(Y_{\hbar }\mathfrak {g})$
provides a homogeneous quantization of the restricted Drinfeld double
$D(Y_{\hbar }\mathfrak {g})$
provides a homogeneous quantization of the restricted Drinfeld double
![]() $\mathfrak {t}\cong D({\mathfrak {t}}_{\scriptscriptstyle {+}})$
of the graded Lie bialgebra
$\mathfrak {t}\cong D({\mathfrak {t}}_{\scriptscriptstyle {+}})$
of the graded Lie bialgebra
![]() $({\mathfrak {t}}_{\scriptscriptstyle {+}},\delta _{\scriptscriptstyle +})$
, realized on the space
$({\mathfrak {t}}_{\scriptscriptstyle {+}},\delta _{\scriptscriptstyle +})$
, realized on the space ![]() .Footnote
2
.Footnote
2
One stipulation to carrying out the quantum double construction in the restricted homogeneous setting is that the canonical element R associated with the pairing between
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
and
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
and
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
, although formally satisfying the relations of (3) in Section 8.1, does not converge in the
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
, although formally satisfying the relations of (3) in Section 8.1, does not converge in the
![]() ${\hbar }$
-adically complete tensor product
${\hbar }$
-adically complete tensor product
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\otimes {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \subset D(Y_{\hbar }\mathfrak {g})\otimes D(Y_{\hbar }\mathfrak {g})$
, and so
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\otimes {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \subset D(Y_{\hbar }\mathfrak {g})\otimes D(Y_{\hbar }\mathfrak {g})$
, and so
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is only topologically quasitriangular. Here, the prefix “topologically” is a bit subtle: it does not refer to the
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is only topologically quasitriangular. Here, the prefix “topologically” is a bit subtle: it does not refer to the
![]() ${\hbar }$
-adic topology and must be handled with care. In Section 9, we shall identify R with the universal R-matrix
${\hbar }$
-adic topology and must be handled with care. In Section 9, we shall identify R with the universal R-matrix
![]() $\mathcal {R}(w-z)\in Y_{\hbar }(\mathfrak {g})^{\otimes 2}[w][\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. This viewpoint allows for a precise interpretation of the relations of (3) in terms of those from Theorem 3.8.
$\mathcal {R}(w-z)\in Y_{\hbar }(\mathfrak {g})^{\otimes 2}[w][\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. This viewpoint allows for a precise interpretation of the relations of (3) in terms of those from Theorem 3.8.
Remark 8.2 There are many competing, though equivalent, variants of the definition of the quantum double. For instance, it may be realized on the tensor product ![]() , as in [Reference Drinfel’d7, Section 13]. Here, we follow the conventions from [Reference Kassel26, Reference Radford39].
, as in [Reference Drinfel’d7, Section 13]. Here, we follow the conventions from [Reference Kassel26, Reference Radford39].
8.3
 $\mathrm {D}Y_{\hbar }\mathfrak {g}$
as a quantum double
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
as a quantum double
We now turn to proving the
![]() ${\hbar }$
-adic variant of the main conjecture from [Reference Khoroshkin and Tolstoy32, Section 2], which postulates that
${\hbar }$
-adic variant of the main conjecture from [Reference Khoroshkin and Tolstoy32, Section 2], which postulates that
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
and
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
and
![]() $D(Y_{\hbar }\mathfrak {g})$
are one and the same (see Theorem 8.4 below).
$D(Y_{\hbar }\mathfrak {g})$
are one and the same (see Theorem 8.4 below).
Recall from the proof of Corollary 7.3 that
![]() $\mathrm {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)\subset (Y_{\hbar }\mathfrak {g}\otimes Y_{\hbar }\mathfrak {g})[\kern-1.2pt\![z^{\pm 1}]\!\kern-1.2pt]$
denotes the
$\mathrm {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)\subset (Y_{\hbar }\mathfrak {g}\otimes Y_{\hbar }\mathfrak {g})[\kern-1.2pt\![z^{\pm 1}]\!\kern-1.2pt]$
denotes the
![]() $\mathbb {Z}$
-graded topological
$\mathbb {Z}$
-graded topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra obtained by completing the graded subalgebra
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra obtained by completing the graded subalgebra
![]() $ {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)$
of
$ {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z)$
of
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes 2}[z;z^{-1}]\!\kern-1.2pt]$
defined in (3.16). Given this notation, we have
$Y_{\hbar }(\mathfrak {g})^{\otimes 2}[z;z^{-1}]\!\kern-1.2pt]$
defined in (3.16). Given this notation, we have
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear maps
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear maps
 $$ \begin{gather*} \pi_z:\mathrm{L}\widehat{Y_{\hbar}\mathfrak{g}}_z\otimes Y_{\hbar}\mathfrak{g}\to \mathrm{L}\widehat{Y_{\hbar}\mathfrak{g}}_z, \quad \pi_z:=m_z\circ (\mathbf{1} \otimes \tau_z),\\ \pi_z^\ast: \mathrm{L}\widehat{Y_{\hbar}\mathfrak{g}}_z \to \mathrm{L}(\widehat{Y_{\hbar}\mathfrak{g}}{\vphantom{Y_{\hbar}\mathfrak{g}}}^{\scriptscriptstyle{(2)}}_z), \quad \pi_z^\ast(y)=(1\otimes y)\mathcal{R}(-z), \end{gather*} $$
$$ \begin{gather*} \pi_z:\mathrm{L}\widehat{Y_{\hbar}\mathfrak{g}}_z\otimes Y_{\hbar}\mathfrak{g}\to \mathrm{L}\widehat{Y_{\hbar}\mathfrak{g}}_z, \quad \pi_z:=m_z\circ (\mathbf{1} \otimes \tau_z),\\ \pi_z^\ast: \mathrm{L}\widehat{Y_{\hbar}\mathfrak{g}}_z \to \mathrm{L}(\widehat{Y_{\hbar}\mathfrak{g}}{\vphantom{Y_{\hbar}\mathfrak{g}}}^{\scriptscriptstyle{(2)}}_z), \quad \pi_z^\ast(y)=(1\otimes y)\mathcal{R}(-z), \end{gather*} $$
where
![]() $m_z$
denotes the multiplication in
$m_z$
denotes the multiplication in
![]() $\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
. These obey a Drinfeld–Yetter right action/left coaction compatibility condition, as the next lemma makes explicit.
$\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
. These obey a Drinfeld–Yetter right action/left coaction compatibility condition, as the next lemma makes explicit.
Lemma 8.3 The pair
![]() $(\pi _z,\pi _z^\ast )$
satisfy the relation
$(\pi _z,\pi _z^\ast )$
satisfy the relation
in
![]() $\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}(Y_{\hbar }\mathfrak {g}\otimes \mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z, \mathrm {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z))$
, where we have set
$\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}(Y_{\hbar }\mathfrak {g}\otimes \mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z, \mathrm {L}(\widehat {Y_{\hbar }\mathfrak {g}}{\vphantom {Y_{\hbar }\mathfrak {g}}}^{\scriptscriptstyle {(2)}}_z))$
, where we have set
Proof This follows from a straightforward modification of the proof of (9) in [Reference Radford39, Lemma 1], using the antipode relations
the counit relation
![]() $m\circ (\mathbf {1} \otimes \varepsilon ) \circ \Delta =\mathbf {1}$
, and the intertwining relation
$m\circ (\mathbf {1} \otimes \varepsilon ) \circ \Delta =\mathbf {1}$
, and the intertwining relation
which itself follows from the identities (1) and (3.20) of Theorem 3.8.
To illustrate this, we apply both sides of the claimed identity to a simple tensor
![]() $x\otimes y\in Y_{\hbar }\mathfrak {g}\otimes \mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
, while exploiting the sumless Sweedler notation
$x\otimes y\in Y_{\hbar }\mathfrak {g}\otimes \mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
, while exploiting the sumless Sweedler notation
![]() $\Delta ^n(x)=x_1\otimes \cdots \otimes x_n$
for iterated coproducts. Expanding the right-hand side of the resulting expression, while using that
$\Delta ^n(x)=x_1\otimes \cdots \otimes x_n$
for iterated coproducts. Expanding the right-hand side of the resulting expression, while using that
![]() ${\dot \blacktriangledown }(x\otimes y)=S^{-1}(x_2)yx_1$
and
${\dot \blacktriangledown }(x\otimes y)=S^{-1}(x_2)yx_1$
and
![]() ${\dot \blacktriangle }(x)=S^{-1}(x_3)x_1\otimes x_2$
, we obtain
${\dot \blacktriangle }(x)=S^{-1}(x_3)x_1\otimes x_2$
, we obtain
 $$ \begin{align*} S^{-1}(x_5)x_3S^{-1}(x_2)\otimes y &\cdot \mathcal{R}(-z)\cdot x_1 \otimes \tau_z(x_4)\\ &= S^{-1}(x_4)\otimes y \cdot \mathcal{R}(-z) \cdot x_1\varepsilon(x_2) \otimes \tau_z(x_3)\\ &=S^{-1}(x_3)\otimes y \cdot \mathcal{R}(-z) \cdot x_1\otimes \tau_z(x_2)\\ &=S^{-1}(x_3)x_2\otimes y\tau_z(x_1) \cdot \mathcal{R}(-z)\\ &=1 \otimes y\tau_z(x_1\varepsilon(x_2)) \cdot \mathcal{R}(-z)\\ &=1\otimes y\tau_z(x) \cdot \mathcal{R}(-z), \end{align*} $$
$$ \begin{align*} S^{-1}(x_5)x_3S^{-1}(x_2)\otimes y &\cdot \mathcal{R}(-z)\cdot x_1 \otimes \tau_z(x_4)\\ &= S^{-1}(x_4)\otimes y \cdot \mathcal{R}(-z) \cdot x_1\varepsilon(x_2) \otimes \tau_z(x_3)\\ &=S^{-1}(x_3)\otimes y \cdot \mathcal{R}(-z) \cdot x_1\otimes \tau_z(x_2)\\ &=S^{-1}(x_3)x_2\otimes y\tau_z(x_1) \cdot \mathcal{R}(-z)\\ &=1 \otimes y\tau_z(x_1\varepsilon(x_2)) \cdot \mathcal{R}(-z)\\ &=1\otimes y\tau_z(x) \cdot \mathcal{R}(-z), \end{align*} $$
where we have applied the intertwining relation (8.3) in the third equality, and the appropriate Hopf relations listed above in each of the remaining equalities. Since
the above computation implies the lemma.
We now come to the main theorem of this section. Recall from Definition 8.1 that we may identify the restricted quantum double
![]() $D(Y_{\hbar }\mathfrak {g})$
with
$D(Y_{\hbar }\mathfrak {g})$
with ![]() as a topological coalgebra over
as a topological coalgebra over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. We further recall that
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. We further recall that
are the
![]() $\mathbb {Z}$
-graded embeddings of topological Hopf algebras over
$\mathbb {Z}$
-graded embeddings of topological Hopf algebras over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
which featured prominently in Theorem 7.5.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
which featured prominently in Theorem 7.5.
Theorem 8.4 The
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphism
is an isomorphism of
![]() $\mathbb {Z}$
-graded topological Hopf algebras
$\mathbb {Z}$
-graded topological Hopf algebras ![]() .
.
Proof We shall first prove that
![]() $\Upsilon $
is an isomorphism of
$\Upsilon $
is an isomorphism of
![]() $\mathbb {Z}$
-graded topological coalgebras over
$\mathbb {Z}$
-graded topological coalgebras over
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, which follows from Theorem 7.5. Afterward, we will use Lemma 8.3 to complete the proof of the theorem by proving that
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, which follows from Theorem 7.5. Afterward, we will use Lemma 8.3 to complete the proof of the theorem by proving that
![]() $\Upsilon $
is an algebra homomorphism
$\Upsilon $
is an algebra homomorphism
![]() $D(Y_{\hbar }\mathfrak {g})\to \mathrm {D}Y_{\hbar }\mathfrak {g}$
. Here, we note that it follows automatically that
$D(Y_{\hbar }\mathfrak {g})\to \mathrm {D}Y_{\hbar }\mathfrak {g}$
. Here, we note that it follows automatically that
![]() $\Upsilon $
intertwines the underlying antipodes, though this is straightforward to verify.
$\Upsilon $
intertwines the underlying antipodes, though this is straightforward to verify.
Proof that
 $\Upsilon $
is an isomorphism of
$\Upsilon $
is an isomorphism of
 $\mathbb {Z}$
-graded coalgebras
$\mathbb {Z}$
-graded coalgebras
Since m,
![]() $\imath $
, and
$\imath $
, and
![]() $\check {\imath }$
are all
$\check {\imath }$
are all
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphisms, the same is true of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphisms, the same is true of
![]() $\Upsilon $
. Moreover, as the coproduct
$\Upsilon $
. Moreover, as the coproduct
![]() $\dot {\Delta }$
of
$\dot {\Delta }$
of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is an algebra homomorphism, it satisfies
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is an algebra homomorphism, it satisfies

Similarly, as the counit
![]() $\dot {\varepsilon }$
of
$\dot {\varepsilon }$
of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is an algebra homomorphism, one has
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is an algebra homomorphism, one has
This proves that
![]() $\Upsilon $
is a
$\Upsilon $
is a
![]() $\mathbb {Z}$
-graded homomorphism of topological coalgebras. Now let us turn to establishing the bijectivity of
$\mathbb {Z}$
-graded homomorphism of topological coalgebras. Now let us turn to establishing the bijectivity of
![]() $\Upsilon $
. As
$\Upsilon $
. As ![]() is a topologically free
is a topologically free
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module with semiclassical limit
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module with semiclassical limit
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {-}})\otimes _{\mathbb {C}} U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
and
$U({\mathfrak {t}}_{\scriptscriptstyle {-}})\otimes _{\mathbb {C}} U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
and
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a flat deformation of
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
is a flat deformation of
![]() $U(\mathfrak {t})$
, Lemma 2.1 asserts that it is sufficient to establish that the semiclassical limit
$U(\mathfrak {t})$
, Lemma 2.1 asserts that it is sufficient to establish that the semiclassical limit
of
![]() $\Upsilon $
is an isomorphism, where
$\Upsilon $
is an isomorphism, where
![]() $\bar {m}, \check {\underline {\imath }}$
, and
$\bar {m}, \check {\underline {\imath }}$
, and
![]() $\underline {\imath }$
are the semiclassical limits of m,
$\underline {\imath }$
are the semiclassical limits of m,
![]() $\check {\imath }$
, and
$\check {\imath }$
, and
![]() $\imath $
, respectively. As
$\imath $
, respectively. As
![]() $\check {\underline {\imath }}$
and
$\check {\underline {\imath }}$
and
![]() $\underline {\imath }$
quantize the natural inclusions of
$\underline {\imath }$
quantize the natural inclusions of
![]() ${\mathfrak {t}}_{\scriptscriptstyle {-}}$
and
${\mathfrak {t}}_{\scriptscriptstyle {-}}$
and
![]() ${\mathfrak {t}}_{\scriptscriptstyle {+}}$
into
${\mathfrak {t}}_{\scriptscriptstyle {+}}$
into
![]() $\mathfrak {t}$
(as was shown in the proof of Lemma 7.4 for
$\mathfrak {t}$
(as was shown in the proof of Lemma 7.4 for
![]() $\check {\underline {\imath }}$
) and
$\check {\underline {\imath }}$
) and
![]() $\bar {m}$
is the multiplication map on
$\bar {m}$
is the multiplication map on
![]() $U(\mathfrak {t})$
, this follows from the Poincaré–Birkhoff–Witt theorem for enveloping algebras and the decomposition
$U(\mathfrak {t})$
, this follows from the Poincaré–Birkhoff–Witt theorem for enveloping algebras and the decomposition ![]() .
.
Proof that
 $\Upsilon $
is an algebra homomorphism
$\Upsilon $
is an algebra homomorphism
By (8.2), we must show that
![]() $\Upsilon \circ \imath _D$
and
$\Upsilon \circ \imath _D$
and
![]() $\Upsilon \circ \check {\imath }_D$
are
$\Upsilon \circ \check {\imath }_D$
are
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphisms and that, in addition,
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphisms and that, in addition,
![]() $\Upsilon $
satisfies the relations
$\Upsilon $
satisfies the relations

By definition of
![]() $\Upsilon $
, we have
$\Upsilon $
, we have
![]() $\Upsilon \circ \imath _D=\imath $
and
$\Upsilon \circ \imath _D=\imath $
and
![]() $\Upsilon \circ \check {\imath }_D=\check {\imath }$
. Moreover, both sides of the identity
$\Upsilon \circ \check {\imath }_D=\check {\imath }$
. Moreover, both sides of the identity
coincide with
![]() $\Upsilon $
, viewed as a map
$\Upsilon $
, viewed as a map ![]() . Hence, we are left to verify the second relation of (8.4), which we shall establish by appealing to the injective
. Hence, we are left to verify the second relation of (8.4), which we shall establish by appealing to the injective
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
![]() $\Phi _z$
from Theorem 4.6. Namely, it is enough to show that
$\Phi _z$
from Theorem 4.6. Namely, it is enough to show that
Since
![]() $\Phi _z$
is an algebra homomorphism satisfying
$\Phi _z$
is an algebra homomorphism satisfying
![]() $\Phi _z\circ \imath =\tau _z$
and
$\Phi _z\circ \imath =\tau _z$
and ![]() (see Lemma 7.4), this is equivalent to
(see Lemma 7.4), this is equivalent to
where
![]() $m_z$
is the product in
$m_z$
is the product in
![]() $\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
. The proof that (8.5) is satisfied follows an argument parallel to that employed to establish Part (a) of Theorem 2 in [Reference Radford39], using Lemma 8.3 in place of [Reference Radford39, (9)]. For the sake of completeness, we give a complete argument below.
$\mathrm {L}\widehat {Y_{\hbar }\mathfrak {g}}_z$
. The proof that (8.5) is satisfied follows an argument parallel to that employed to establish Part (a) of Theorem 2 in [Reference Radford39], using Lemma 8.3 in place of [Reference Radford39, (9)]. For the sake of completeness, we give a complete argument below.
Applying the left-hand side of (8.5) to an arbitrary simple tensor
![]() $x\otimes f$
, we obtain
$x\otimes f$
, we obtain
which, by Lemma 8.3, may be rewritten as
On the other hand, by definition of ![]() ,
,
![]() $\rhd $
, and
$\rhd $
, and
![]() $\lhd $
, the right-hand side of (8.5) evaluated on
$\lhd $
, the right-hand side of (8.5) evaluated on
![]() $x\otimes f$
is
$x\otimes f$
is
where we have employed the sumless Sweedler notation
![]() $\Delta (x)=x_1\otimes x_2$
and
$\Delta (x)=x_1\otimes x_2$
and ![]() . That this coincides with the expression (8.6) for
. That this coincides with the expression (8.6) for ![]() is a consequence of the following general computation. For each
is a consequence of the following general computation. For each
![]() $a\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
and
$a\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
and
![]() $b\in Y_{\hbar }\mathfrak {g}$
, we have
$b\in Y_{\hbar }\mathfrak {g}$
, we have

where we have set
![]() $x\bullet a= \dot {\blacktriangledown }(x\otimes a)$
and in the first and second equalities we have used the (sumless) Sweedler-type notation
$x\bullet a= \dot {\blacktriangledown }(x\otimes a)$
and in the first and second equalities we have used the (sumless) Sweedler-type notation
![]() $\dot {\blacktriangle }(x)=x^{(1)}\otimes x^{(2)}$
. This completes the proof of (8.5), and thus the proof that
$\dot {\blacktriangle }(x)=x^{(1)}\otimes x^{(2)}$
. This completes the proof of (8.5), and thus the proof that
![]() $\Upsilon $
is an algebra homomorphism.
$\Upsilon $
is an algebra homomorphism.
9 The universal R-matrix
In this final section, we establish the last assertion of Theorem I, which identifies the universal R-matrix ![]() of the Yangian double
of the Yangian double
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}\cong D(Y_{\hbar }\mathfrak {g})$
with Drinfeld’s universal R-matrix
$\mathrm {D}Y_{\hbar }\mathfrak {g}\cong D(Y_{\hbar }\mathfrak {g})$
with Drinfeld’s universal R-matrix
![]() $\mathcal {R}(z)$
(see Theorem 9.6). Though this in fact follows without too much effort from the results of Sections 7 and 8, constructing
$\mathcal {R}(z)$
(see Theorem 9.6). Though this in fact follows without too much effort from the results of Sections 7 and 8, constructing ![]() precisely does require some care. After laying the groundwork in Sections 9.1 and 9.2, we define
precisely does require some care. After laying the groundwork in Sections 9.1 and 9.2, we define ![]() and prove our last main result in Section 9.3. The final two subsections – Sections 9.4 and 9.5 – are devoted to providing additional context pertinent to this theorem.
and prove our last main result in Section 9.3. The final two subsections – Sections 9.4 and 9.5 – are devoted to providing additional context pertinent to this theorem.
9.1 The isomorphism
 $\Theta $
$\Theta $
Let
![]() $\theta $
denote the canonical
$\theta $
denote the canonical
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module injection
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module injection
determined on simple tensors by
![]() $\theta (x\otimes f)(y)=f(y)x$
. This injection is a homomorphism of topological
$\theta (x\otimes f)(y)=f(y)x$
. This injection is a homomorphism of topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras provided we equip
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras provided we equip
![]() $\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g},Y_{\hbar }\mathfrak {g})$
with the convolution product
$\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g},Y_{\hbar }\mathfrak {g})$
with the convolution product
and identity element
![]() $\iota \circ \varepsilon $
, where m,
$\iota \circ \varepsilon $
, where m,
![]() $\Delta $
,
$\Delta $
,
![]() $\iota $
, and
$\iota $
, and
![]() $\varepsilon $
are the multiplication, coproduct, unit, and counit of
$\varepsilon $
are the multiplication, coproduct, unit, and counit of
![]() $Y_{\hbar }\mathfrak {g}$
, respectively. Our main goal in this subsection is to identity a natural extension of
$Y_{\hbar }\mathfrak {g}$
, respectively. Our main goal in this subsection is to identity a natural extension of
![]() $\theta $
which is an isomorphism.
$\theta $
which is an isomorphism.
Let us begin by noting some topological properties of the homomorphism space
![]() $\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g},Y_{\hbar }\mathfrak {g})$
. As
$\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g},Y_{\hbar }\mathfrak {g})$
. As
![]() $Y_{\hbar }\mathfrak {g}$
and
$Y_{\hbar }\mathfrak {g}$
and
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
are topologically free with semiclassical limits
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
are topologically free with semiclassical limits
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
and
$U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
and
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
, respectively,
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}})$
, respectively,
![]() $\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g},Y_{\hbar }\mathfrak {g})$
is a topologically free
$\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g},Y_{\hbar }\mathfrak {g})$
is a topologically free
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules with
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules with
In addition,
![]() $\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g},Y_{\hbar }\mathfrak {g})$
is a Hausdorff and complete topological space with respect to the topology associated with the descending filtration
$\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g},Y_{\hbar }\mathfrak {g})$
is a Hausdorff and complete topological space with respect to the topology associated with the descending filtration
![]() ${\mathbb {E}}_\bullet $
of closed
${\mathbb {E}}_\bullet $
of closed
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-submodules defined by
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-submodules defined by
where we have set
![]() $\mathbf {J}_n=\bigoplus _{k< n}{\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})_k$
with
$\mathbf {J}_n=\bigoplus _{k< n}{\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})_k$
with
![]() $\mathbf {J}_{0}=\{0\}$
. Said in more algebraic terms, the natural
$\mathbf {J}_{0}=\{0\}$
. Said in more algebraic terms, the natural
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module homomorphism
is an isomorphism, as is readily verified. Moreover, as the coproduct
![]() $\Delta $
on
$\Delta $
on
![]() $Y_{\hbar }\mathfrak {g}$
is graded,
$Y_{\hbar }\mathfrak {g}$
is graded,
![]() ${\mathbb {E}}_\bullet $
is a descending filtration of ideals and the above is an isomorphism of
${\mathbb {E}}_\bullet $
is a descending filtration of ideals and the above is an isomorphism of
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras.
We now turn toward enlarging the domain of
![]() $\theta $
. For each
$\theta $
. For each
![]() $n\in \mathbb {Z}$
, let
$n\in \mathbb {Z}$
, let
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{\scriptscriptstyle (n)}$
denote the closure of the
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{\scriptscriptstyle (n)}$
denote the closure of the
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-submodule of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-submodule of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
generated by
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
generated by
![]() $\bigoplus _{k\geq n} {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{-k}$
. Since
$\bigoplus _{k\geq n} {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{-k}$
. Since
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _k\subset {\hbar }{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{k-1}$
for
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _k\subset {\hbar }{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{k-1}$
for
![]() $k>0$
,
$k>0$
,
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{\scriptscriptstyle (0)}={\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
and we have a descending
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{\scriptscriptstyle (0)}={\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
and we have a descending
![]() $\mathbb {N}$
-filtration
$\mathbb {N}$
-filtration
We may thus introduce the topological tensor product
Since
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is topologically generated as a
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is topologically generated as a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra by the space
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra by the space
![]() $\bigoplus _{k>0} {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{-k}$
and, for each
$\bigoplus _{k>0} {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{-k}$
and, for each
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $\bigoplus _{k\geq n} {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{-k}$
is stable under multiplication by any x in this space, we see that each
$\bigoplus _{k\geq n} {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{-k}$
is stable under multiplication by any x in this space, we see that each
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{\scriptscriptstyle (n)}$
is an ideal in
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{\scriptscriptstyle (n)}$
is an ideal in
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. It follows that
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. It follows that
![]() $Y_{\hbar }\mathfrak {g} \,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is a
$Y_{\hbar }\mathfrak {g} \,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra.
To see that
![]() $Y_{\hbar }\mathfrak {g} \,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is a topologically free
$Y_{\hbar }\mathfrak {g} \,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is a topologically free
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module, let us introduce the classical spaces
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module, let us introduce the classical spaces
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star _{\scriptscriptstyle (n)}$
and
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star _{\scriptscriptstyle (n)}$
and
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {+}})\,\widetilde {\otimes }\,\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
by setting
$U({\mathfrak {t}}_{\scriptscriptstyle {+}})\,\widetilde {\otimes }\,\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star $
by setting
 $$ \begin{gather*} \mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star_{\scriptscriptstyle(n)}:= \bigoplus_{k\geq n}\mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star_{{-k}},\\ U({\mathfrak{t}}_{\scriptscriptstyle{+}})\,\widetilde{\otimes}\,\mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star:=\prod_{n\in \mathbb{N}} U({\mathfrak{t}}_{\scriptscriptstyle{+}})\otimes_{\mathbb{C}} \mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star_{-n} \cong \varprojlim_{n} U({\mathfrak{t}}_{\scriptscriptstyle{+}})\otimes_{\mathbb{C}} (\mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star/\mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star_{\scriptscriptstyle (n)}). \end{gather*} $$
$$ \begin{gather*} \mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star_{\scriptscriptstyle(n)}:= \bigoplus_{k\geq n}\mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star_{{-k}},\\ U({\mathfrak{t}}_{\scriptscriptstyle{+}})\,\widetilde{\otimes}\,\mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star:=\prod_{n\in \mathbb{N}} U({\mathfrak{t}}_{\scriptscriptstyle{+}})\otimes_{\mathbb{C}} \mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star_{-n} \cong \varprojlim_{n} U({\mathfrak{t}}_{\scriptscriptstyle{+}})\otimes_{\mathbb{C}} (\mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star/\mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star_{\scriptscriptstyle (n)}). \end{gather*} $$
Lemma 9.1 The
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra
![]() $Y_{\hbar }\mathfrak {g} \,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is topologically free with
$Y_{\hbar }\mathfrak {g} \,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is topologically free with
Proof Let ![]() be any fixed
be any fixed
![]() $\mathbb {Z}$
-graded isomorphism of topological
$\mathbb {Z}$
-graded isomorphism of topological
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules. We claim that
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules. We claim that
To see this, fix
![]() $n\in \mathbb {N}$
. Since
$n\in \mathbb {N}$
. Since
![]() $\unicode{x3bd} _\star $
is graded, we have
$\unicode{x3bd} _\star $
is graded, we have
As
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star _{\scriptscriptstyle (n)}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
is a closed
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star _{\scriptscriptstyle (n)}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
is a closed
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-submodule of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-submodule of
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star [\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, we get
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star [\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, we get
![]() $\unicode{x3bd} _\star ({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{\scriptscriptstyle {(n)}})\subset \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star _{\scriptscriptstyle (n)}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. Conversely, if
$\unicode{x3bd} _\star ({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{\scriptscriptstyle {(n)}})\subset \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star _{\scriptscriptstyle (n)}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
. Conversely, if
![]() $\sum _{a\geq 0}x_a{\hbar }^a\in \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star _{\scriptscriptstyle (n)}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, then
$\sum _{a\geq 0}x_a{\hbar }^a\in \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star _{\scriptscriptstyle (n)}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
, then
![]() $y_a:=\unicode{x3bd} _\star ^{-1}(x_a)\in \bigoplus _{k\geq n} {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{-k}$
for each
$y_a:=\unicode{x3bd} _\star ^{-1}(x_a)\in \bigoplus _{k\geq n} {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{-k}$
for each
![]() $a\in \mathbb {N}$
. Therefore, we have
$a\in \mathbb {N}$
. Therefore, we have

which completes the proof of (9.3). The statement of the lemma now follows from the sequence of isomorphisms
 $$ \begin{align*} Y_{\hbar}\mathfrak{g}\otimes {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star / Y_{\hbar}\mathfrak{g} \otimes {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star_{\scriptscriptstyle(n)}&\cong (U({\mathfrak{t}}_{\scriptscriptstyle{+}})\otimes_{\mathbb{C}} \mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star)[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt]/(U({\mathfrak{t}}_{\scriptscriptstyle{+}})\otimes_{\mathbb{C}} \mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star_{\scriptscriptstyle (n)})[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt] \\ &\cong \left(U({\mathfrak{t}}_{\scriptscriptstyle{+}})\otimes_{\mathbb{C}} (\mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star/\mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star_{\scriptscriptstyle (n)})\right)[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt].\\[-37pt] \end{align*} $$
$$ \begin{align*} Y_{\hbar}\mathfrak{g}\otimes {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star / Y_{\hbar}\mathfrak{g} \otimes {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star_{\scriptscriptstyle(n)}&\cong (U({\mathfrak{t}}_{\scriptscriptstyle{+}})\otimes_{\mathbb{C}} \mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star)[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt]/(U({\mathfrak{t}}_{\scriptscriptstyle{+}})\otimes_{\mathbb{C}} \mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star_{\scriptscriptstyle (n)})[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt] \\ &\cong \left(U({\mathfrak{t}}_{\scriptscriptstyle{+}})\otimes_{\mathbb{C}} (\mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star/\mathsf{S}({\hbar}{\mathfrak{t}}_{\scriptscriptstyle{+}}){\vphantom{)}}^\star_{\scriptscriptstyle (n)})\right)[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt].\\[-37pt] \end{align*} $$
The next result outputs the desired extensions of
![]() $\theta $
.
$\theta $
.
Proposition 9.2 The injection
![]() $\theta $
extends to an isomorphism of
$\theta $
extends to an isomorphism of
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras
Proof Let
![]() ${\mathbb {E}}_\bullet $
be the filtration of
${\mathbb {E}}_\bullet $
be the filtration of
![]() $\mathbb {E}:=\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g},Y_{\hbar }\mathfrak {g})$
defined in (9.2). Then
$\mathbb {E}:=\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g},Y_{\hbar }\mathfrak {g})$
defined in (9.2). Then
Indeed, this follows from the definition of
![]() $\theta $
and the fact that if
$\theta $
and the fact that if
![]() $f\in \bigoplus _{k\geq n}{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{-k}$
and
$f\in \bigoplus _{k\geq n}{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{-k}$
and
![]() $x\in \mathbf {J}_{n}$
, then
$x\in \mathbf {J}_{n}$
, then
![]() $f(x)=0$
. Hence, we obtain
$f(x)=0$
. Hence, we obtain
As
![]() $Y_{\hbar }\mathfrak {g}$
and
$Y_{\hbar }\mathfrak {g}$
and
![]() $\mathbb {E}$
are topologically free, to show
$\mathbb {E}$
are topologically free, to show
![]() $\Theta $
is an isomorphism, it is sufficient to show its semiclassical limit
$\Theta $
is an isomorphism, it is sufficient to show its semiclassical limit
![]() $\bar \Theta $
is (see Lemma 2.1). Employing the identifications of (9.1) and Lemma 9.1, we see that
$\bar \Theta $
is (see Lemma 2.1). Employing the identifications of (9.1) and Lemma 9.1, we see that
![]() $\bar {\Theta }$
coincides with the isomorphism
$\bar {\Theta }$
coincides with the isomorphism
uniquely extending the canonical map
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {+}})\otimes _{\mathbb {C}} \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star \hookrightarrow \mathrm {Hom}_{\mathbb {C}} (\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}),U({\mathfrak {t}}_{\scriptscriptstyle {+}}))$
, which is the semiclassical limit
$U({\mathfrak {t}}_{\scriptscriptstyle {+}})\otimes _{\mathbb {C}} \mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}){\vphantom {)}}^\star \hookrightarrow \mathrm {Hom}_{\mathbb {C}} (\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}),U({\mathfrak {t}}_{\scriptscriptstyle {+}}))$
, which is the semiclassical limit
![]() $\bar \theta $
of
$\bar \theta $
of
![]() $\theta $
, by continuity.
$\theta $
, by continuity.
We now give two remarks pertinent to the above discussion.
Remark 9.3 By Proposition 9.2, we may introduce the
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-subalgebra
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-subalgebra
By definition, it comes equipped with an isomorphism
extending the injection
![]() $\theta |_{{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\otimes {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star }$
. It is worth noting that, by following the above arguments, it is easy to see that
$\theta |_{{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\otimes {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star }$
. It is worth noting that, by following the above arguments, it is easy to see that
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
admits the equivalent description
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
admits the equivalent description
Suppose now that
![]() $\varphi ,\gamma \in \mathrm {End}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g})$
with
$\varphi ,\gamma \in \mathrm {End}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g})$
with
![]() $\gamma $
homogeneous of degree
$\gamma $
homogeneous of degree
![]() $a\in \mathbb {Z}$
. Then
$a\in \mathbb {Z}$
. Then
![]() $\varphi \otimes \gamma ^t$
uniquely extends to an element of
$\varphi \otimes \gamma ^t$
uniquely extends to an element of
![]() $\mathrm {End}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\,\widetilde {\otimes }\,{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star )$
and
$\mathrm {End}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\,\widetilde {\otimes }\,{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star )$
and
![]() $\Theta $
has the property that
$\Theta $
has the property that
Remark 9.4 The argument used to establish Proposition 6.2 implies that the natural
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
is an embedding. Hence, we can (and shall) view
![]() $\mathrm {End}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}(Y_{\hbar }\mathfrak {g})$
as a subalgebra of
$\mathrm {End}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}(Y_{\hbar }\mathfrak {g})$
as a subalgebra of
![]() $\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g},Y_{\hbar }\mathfrak {g})$
. We may thus introduce
$\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g},Y_{\hbar }\mathfrak {g})$
. We may thus introduce
![]() $Y_{\hbar }\mathfrak {g}\,\widetilde {\otimes }\,Y_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \subset Y_{\hbar }\mathfrak {g}\,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
by setting
$Y_{\hbar }\mathfrak {g}\,\widetilde {\otimes }\,Y_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \subset Y_{\hbar }\mathfrak {g}\,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
by setting
We then have
where the right-hand side consists of all
![]() $f\in \mathrm {End}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}(Y_{\hbar }\mathfrak {g})$
for which
$f\in \mathrm {End}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}(Y_{\hbar }\mathfrak {g})$
for which
![]() $f({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g})\subset {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
.
$f({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g})\subset {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
.
9.2 The restriction
 $\Theta _\chi $
$\Theta _\chi $
We now give a few comments which concern the triangular decompositions of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
and
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
and
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. For each choice of the symbol
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. For each choice of the symbol
![]() $\chi $
, let
$\chi $
, let
![]() $\pi ^\chi :{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\to {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}$
denote the
$\pi ^\chi :{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\to {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}$
denote the
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear projection associated with the triangular decomposition of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear projection associated with the triangular decomposition of
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
, as defined in Section 6.5. These projections give rise to
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
, as defined in Section 6.5. These projections give rise to
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module embeddings
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module embeddings
We shall henceforth adopt the viewpoint that
![]() $\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g},Y_{\hbar }^\chi \mathfrak {g})$
is a submodule of
$\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g},Y_{\hbar }^\chi \mathfrak {g})$
is a submodule of
![]() $\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g},Y_{\hbar }\mathfrak {g})$
, with the above identification assumed. The restriction
$\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g},Y_{\hbar }\mathfrak {g})$
, with the above identification assumed. The restriction
![]() $\theta _\chi $
of
$\theta _\chi $
of
![]() $\theta $
to
$\theta $
to
![]() $Y_{\hbar }^\chi \mathfrak {g}\otimes {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
is then a
$Y_{\hbar }^\chi \mathfrak {g}\otimes {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
is then a
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module injection
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module injection
Following the above procedure, we may introduce the
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra
where
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star _{\scriptscriptstyle (n)}$
is the closure of the
${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star _{\scriptscriptstyle (n)}$
is the closure of the
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-submodule of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-submodule of
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
generated by the direct sum
${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
generated by the direct sum
![]() $\bigoplus _{k\geq n}{\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star _{-k}$
. The above arguments show that this completed tensor product is a flat
$\bigoplus _{k\geq n}{\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star _{-k}$
. The above arguments show that this completed tensor product is a flat
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra deformation of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra deformation of
It follows that the natural algebra homomorphism
![]() $Y_{\hbar }^\chi \mathfrak {g} \,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star \to Y_{\hbar }\mathfrak {g}\,\widetilde {\otimes }\,{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is injective and, by the proof of Proposition 9.2, that
$Y_{\hbar }^\chi \mathfrak {g} \,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star \to Y_{\hbar }\mathfrak {g}\,\widetilde {\otimes }\,{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is injective and, by the proof of Proposition 9.2, that
![]() $\theta _\chi $
uniquely extends to an isomorphism of
$\theta _\chi $
uniquely extends to an isomorphism of
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-modules
which coincides with the restriction of
![]() $\Theta $
to
$\Theta $
to
![]() $Y_{\hbar }^\chi \mathfrak {g}\,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
. In particular, since
$Y_{\hbar }^\chi \mathfrak {g}\,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
. In particular, since
![]() $Y_{\hbar }^\chi \mathfrak {g}\,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
is a subalgebra of
$Y_{\hbar }^\chi \mathfrak {g}\,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
is a subalgebra of
![]() $Y_{\hbar }\mathfrak {g}\,\widetilde {\otimes }\,{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
, the space
$Y_{\hbar }\mathfrak {g}\,\widetilde {\otimes }\,{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
, the space
![]() $\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g},Y_{\hbar }^\chi \mathfrak {g})$
is a subalgebra of
$\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g},Y_{\hbar }^\chi \mathfrak {g})$
is a subalgebra of
![]() $\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g},Y_{\hbar }\mathfrak {g})$
and
$\mathrm {Hom}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g},Y_{\hbar }\mathfrak {g})$
and
![]() $\Theta _\chi $
is an isomorphism of
$\Theta _\chi $
is an isomorphism of
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras.
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras.
Finally, as in Remarks 9.3 and 9.4, we set
 $$ \begin{gather*} {\dot{\mathsf{Y}}}_{\hbar}^{\chi}\mathfrak{g}\,\widetilde{\otimes}\, {\dot{\mathsf{Y}}}_{\hbar}^{\chi}\mathfrak{g}{\vphantom{)}}^\star:=\Theta^{-1}_\chi(\mathrm{End}_{\mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt]}({\dot{\mathsf{Y}}}_{\hbar}^{\chi}\mathfrak{g}))\cong \varprojlim_n({\dot{\mathsf{Y}}}_{\hbar}^{\chi}\mathfrak{g}\otimes {\dot{\mathsf{Y}}}_{\hbar}^{\chi}\mathfrak{g}{\vphantom{)}}^\star / {\dot{\mathsf{Y}}}_{\hbar}^{\chi}\mathfrak{g}\otimes {\dot{\mathsf{Y}}}_{\hbar}^{\chi}\mathfrak{g}{\vphantom{)}}^\star_{\scriptscriptstyle(n)}),\\ Y_{\hbar}^\chi\mathfrak{g}\,\widetilde{\otimes}\, Y_{\hbar}^\chi\mathfrak{g}{\vphantom{)}}^\star:=\Theta^{-1}_\chi(\mathrm{End}_{\mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt]}(Y_{\hbar}^{\chi}\mathfrak{g})). \end{gather*} $$
$$ \begin{gather*} {\dot{\mathsf{Y}}}_{\hbar}^{\chi}\mathfrak{g}\,\widetilde{\otimes}\, {\dot{\mathsf{Y}}}_{\hbar}^{\chi}\mathfrak{g}{\vphantom{)}}^\star:=\Theta^{-1}_\chi(\mathrm{End}_{\mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt]}({\dot{\mathsf{Y}}}_{\hbar}^{\chi}\mathfrak{g}))\cong \varprojlim_n({\dot{\mathsf{Y}}}_{\hbar}^{\chi}\mathfrak{g}\otimes {\dot{\mathsf{Y}}}_{\hbar}^{\chi}\mathfrak{g}{\vphantom{)}}^\star / {\dot{\mathsf{Y}}}_{\hbar}^{\chi}\mathfrak{g}\otimes {\dot{\mathsf{Y}}}_{\hbar}^{\chi}\mathfrak{g}{\vphantom{)}}^\star_{\scriptscriptstyle(n)}),\\ Y_{\hbar}^\chi\mathfrak{g}\,\widetilde{\otimes}\, Y_{\hbar}^\chi\mathfrak{g}{\vphantom{)}}^\star:=\Theta^{-1}_\chi(\mathrm{End}_{\mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt]}(Y_{\hbar}^{\chi}\mathfrak{g})). \end{gather*} $$
9.3 Canonical tensors and universal R-matrices
By Proposition 9.2, we may introduce R and
![]() $R^\chi $
in
$R^\chi $
in
![]() $Y_{\hbar }\mathfrak {g}\,\widetilde {\otimes }\,{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
, for each choice of
$Y_{\hbar }\mathfrak {g}\,\widetilde {\otimes }\,{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
, for each choice of
![]() $\chi $
, as the elements
$\chi $
, as the elements
That is, R and
![]() $R^\chi $
are the canonical elements associated with the Hopf pairing
$R^\chi $
are the canonical elements associated with the Hopf pairing
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\times {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \to \mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
and its restriction to
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\times {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \to \mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
and its restriction to
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}\times {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
, respectively.
${\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}\times {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
, respectively.
As
![]() $\mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}}$
and
$\mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}}$
and
![]() $\mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}}$
coincide with
$\mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}}$
coincide with
![]() $\mathbf {1}_{Y_{\hbar }\mathfrak {g}}$
and
$\mathbf {1}_{Y_{\hbar }\mathfrak {g}}$
and
![]() $\mathbf {1}_{Y_{\hbar }^\chi \mathfrak {g}}$
under the identifications of Remark 9.4 and Section 9.2, respectively, R (resp.
$\mathbf {1}_{Y_{\hbar }^\chi \mathfrak {g}}$
under the identifications of Remark 9.4 and Section 9.2, respectively, R (resp.
![]() $R^\chi $
) is also the canonical element defined by the pairing between
$R^\chi $
) is also the canonical element defined by the pairing between
![]() $Y_{\hbar }\mathfrak {g}$
and its restricted dual
$Y_{\hbar }\mathfrak {g}$
and its restricted dual
![]() $Y_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
(resp.
$Y_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
(resp.
![]() $Y_{\hbar }^\chi \mathfrak {g}$
and
$Y_{\hbar }^\chi \mathfrak {g}$
and
![]() $Y_{\hbar }^\chi \mathfrak {g}{\vphantom {)}}^\star $
). In particular, we have
$Y_{\hbar }^\chi \mathfrak {g}{\vphantom {)}}^\star $
). In particular, we have
It is worth pointing out that one can immediately deduce a number of properties that R and
![]() $R^\chi $
satisfy using only elementary properties of
$R^\chi $
satisfy using only elementary properties of
![]() $\Theta $
. For instance:
$\Theta $
. For instance:
-
(R1) Applying (9.4) with
 $\gamma =\mathbf {1}$
while using that
$\gamma =\mathbf {1}$
while using that
 $\Theta (1\otimes f)=\iota \circ f$
recovers the characteristic identities for all
$\Theta (1\otimes f)=\iota \circ f$
recovers the characteristic identities for all $$ \begin{align*} (\iota\circ f)\otimes \mathbf{1} \cdot R=1\otimes f\quad \text{ and }\quad (\iota\circ f^\chi)\otimes \mathbf{1} \cdot R^\chi=1\otimes f^\chi \end{align*} $$
$$ \begin{align*} (\iota\circ f)\otimes \mathbf{1} \cdot R=1\otimes f\quad \text{ and }\quad (\iota\circ f^\chi)\otimes \mathbf{1} \cdot R^\chi=1\otimes f^\chi \end{align*} $$
 $f\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
and
$f\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
and
 $f^\chi \in {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
.
$f^\chi \in {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
.
-
(R2) Taking
 $\varphi =\gamma =\omega $
in (9.4) with
$\varphi =\gamma =\omega $
in (9.4) with
 $y=\mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}}$
or
$y=\mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}}$
or
 $\mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }^{\mp }\mathfrak {g}}$
while using that
$\mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }^{\mp }\mathfrak {g}}$
while using that
 $\mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}}=\omega \circ \mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }^{\mp }\mathfrak {g}}\circ \omega $
gives rise to the identities
$\mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}}=\omega \circ \mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }^{\mp }\mathfrak {g}}\circ \omega $
gives rise to the identities  $$ \begin{align*} R=(\omega\otimes \omega^t)R \quad\text{ and }\quad R^\pm=(\omega\otimes \omega^t)(R^\mp). \end{align*} $$
$$ \begin{align*} R=(\omega\otimes \omega^t)R \quad\text{ and }\quad R^\pm=(\omega\otimes \omega^t)(R^\mp). \end{align*} $$
-
(R3) Since
 $\mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}}$
is a
$\mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}}$
is a
 $\mathfrak {g}$
-invariant element of
$\mathfrak {g}$
-invariant element of
 $\mathrm {End}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g})$
and
$\mathrm {End}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g})$
and
 $\Theta $
is a
$\Theta $
is a
 $\mathfrak {g}$
-module intertwiner, R is a
$\mathfrak {g}$
-module intertwiner, R is a
 $\mathfrak {g}$
-invariant element
$\mathfrak {g}$
-invariant element
 ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. Using the multiplication in
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
. Using the multiplication in
 $D(Y_{\hbar }\mathfrak {g})$
, this can be written as Similarly,
$D(Y_{\hbar }\mathfrak {g})$
, this can be written as Similarly, $$ \begin{align*} [x\otimes 1 + 1\otimes x,R]=0 \quad \forall\; x\in \mathfrak{g}. \end{align*} $$
$$ \begin{align*} [x\otimes 1 + 1\otimes x,R]=0 \quad \forall\; x\in \mathfrak{g}. \end{align*} $$
 $R^\pm $
and
$R^\pm $
and
 $R^0$
are both
$R^0$
are both
 $\mathfrak {h}$
-invariant.
$\mathfrak {h}$
-invariant.
In addition, the standard quantum double arguments show that R satisfies the quasitriangularity relations of (3) in Section 8.1 in suitable completions of tensor powers of
![]() $D(Y_{\hbar }\mathfrak {g})$
. For instance, the cabling identities
$D(Y_{\hbar }\mathfrak {g})$
. For instance, the cabling identities
![]() $\Delta \otimes \mathbf {1}(R)=R_{13}R_{23}$
and
$\Delta \otimes \mathbf {1}(R)=R_{13}R_{23}$
and ![]() are equivalent to the simple identities
are equivalent to the simple identities
in the convolution algebras
 $$ \begin{gather*} ({\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}^{\otimes 2})\,\widetilde{\otimes}\,{\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star:=\mathrm{Hom}_{\mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt]}({\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g},{\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}^{\otimes 2}),\\ {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}\,\widetilde{\otimes}\, ({\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star)^{\otimes 2}:=\mathrm{Hom}_{\mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt]}({\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}^{\otimes 2},{\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}), \end{gather*} $$
$$ \begin{gather*} ({\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}^{\otimes 2})\,\widetilde{\otimes}\,{\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star:=\mathrm{Hom}_{\mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt]}({\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g},{\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}^{\otimes 2}),\\ {\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}\,\widetilde{\otimes}\, ({\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}{\vphantom{)}}^\star)^{\otimes 2}:=\mathrm{Hom}_{\mathbb{C}[\kern-1.2pt\![{\hbar}]\!\kern-1.2pt]}({\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}^{\otimes 2},{\dot{\mathsf{Y}}}_{\hbar}\mathfrak{g}), \end{gather*} $$
respectively, where
![]() $\mathbf {1}^{(a)}_{{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}}:{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\to {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}^{\otimes 2}$
is given by
$\mathbf {1}^{(a)}_{{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}}:{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\to {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}^{\otimes 2}$
is given by
![]() $x\mapsto x^{(a)}$
.
$x\mapsto x^{(a)}$
.
Our main goal in this section is to establish the remaining assertion of Theorem I from Section 1.1, which claims that R can be identified with the universal R-matrix of the Yangian. This interpretation allows for a precise framework for understanding the topological quasitriangular structure on
![]() $D(Y_{\hbar }\mathfrak {g})$
alluded to above. To achieve this, we will need the next lemma, where
$D(Y_{\hbar }\mathfrak {g})$
alluded to above. To achieve this, we will need the next lemma, where ![]() is as in Proposition 7.1.
is as in Proposition 7.1.
Lemma 9.5
![]() extends to an injective
extends to an injective
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
Proof It is sufficient to show ![]() extends to an injective
extends to an injective
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
Since ![]() ,
, ![]() induces a family of compatible algebra homomorphisms
induces a family of compatible algebra homomorphisms
Taking the projective limit gives the desired extension ![]() . We are left to verify that it is indeed injective, which is perhaps a bit subtle (given that
. We are left to verify that it is indeed injective, which is perhaps a bit subtle (given that ![]() is injective), but not difficult. As
is injective), but not difficult. As
![]() $Y_{\hbar }\mathfrak {g}\, \widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is separated with respect to the
$Y_{\hbar }\mathfrak {g}\, \widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
is separated with respect to the
![]() ${\hbar }$
-adic topology and
${\hbar }$
-adic topology and
![]() $Y_{\hbar }\mathfrak {g}^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
is torsion free, this can be done by verifying that the semiclassical limit of
$Y_{\hbar }\mathfrak {g}^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
is torsion free, this can be done by verifying that the semiclassical limit of ![]() is injective. This is the linear map
is injective. This is the linear map
which is ![]() on the n-th component of the direct product, where
on the n-th component of the direct product, where ![]() is the semiclassical limit of
is the semiclassical limit of ![]() and
and
![]() $\widehat {U({\mathfrak {t}}_{\scriptscriptstyle {+}})}_z=\prod _{n\in \mathbb {N}}U({\mathfrak {t}}_{\scriptscriptstyle {+}})_n z^{-n}$
. The desired result now follows from the fact that
$\widehat {U({\mathfrak {t}}_{\scriptscriptstyle {+}})}_z=\prod _{n\in \mathbb {N}}U({\mathfrak {t}}_{\scriptscriptstyle {+}})_n z^{-n}$
. The desired result now follows from the fact that ![]() is injective, which can be seen as a consequence of the equality
is injective, which can be seen as a consequence of the equality ![]() and that, by [Reference Wendlandt41, Theorem 6.2] and the proof of Lemma 7.4, both
and that, by [Reference Wendlandt41, Theorem 6.2] and the proof of Lemma 7.4, both
![]() $\Phi $
and
$\Phi $
and
![]() $\check {\imath }$
have injective semiclassical limits.
$\check {\imath }$
have injective semiclassical limits.
To recover the desired result as stated in (2) of Theorem I, we now translate some of the above constructions and results from
![]() $D(Y_{\hbar }\mathfrak {g})$
to
$D(Y_{\hbar }\mathfrak {g})$
to
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
using the isomorphism
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
using the isomorphism
![]() $\Upsilon $
from Theorem 8.4 or, equivalently, the Hopf algebra embeddings
$\Upsilon $
from Theorem 8.4 or, equivalently, the Hopf algebra embeddings
![]() $\imath $
and
$\imath $
and
![]() $\check {\imath }$
from Theorem 7.5. Let us set
$\check {\imath }$
from Theorem 7.5. Let us set
This definition is such that isomorphism
extends to an isomorphism of
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebras
Armed with these preliminaries, we may now introduce the universal R-matrix of the Yangian double
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
as the element
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
as the element
where, for each choice of A and B,
![]() $A\dot {\otimes } B$
denotes the image of
$A\dot {\otimes } B$
denotes the image of
![]() $A\widetilde {\otimes }B$
under
$A\widetilde {\otimes }B$
under
![]() $\imath \,\dot {\otimes }\,\check {\imath }$
. Similarly, we define the
$\imath \,\dot {\otimes }\,\check {\imath }$
. Similarly, we define the
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
analogues of
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
analogues of
![]() $R^\pm $
and
$R^\pm $
and
![]() $R^0$
by setting
$R^0$
by setting
By Theorem 4.6 and Lemma 7.4,
![]() $\Phi _z$
satisfies
$\Phi _z$
satisfies
![]() $\Phi _z\circ \imath =\tau _z$
and
$\Phi _z\circ \imath =\tau _z$
and ![]() . Lemma 9.5 therefore implies that the restriction of
. Lemma 9.5 therefore implies that the restriction of
![]() $\Phi _w\otimes \Phi _z$
to
$\Phi _w\otimes \Phi _z$
to ![]() extends to an injective
extends to an injective
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-algebra homomorphism
Indeed, we may set ![]() . With this homomorphism at our disposal, we are now in a position to state and prove the last main result outlined in Section 1.1.
. With this homomorphism at our disposal, we are now in a position to state and prove the last main result outlined in Section 1.1.
Theorem 9.6 The following identities hold in
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes 2}[w][\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
:
$Y_{\hbar }(\mathfrak {g})^{\otimes 2}[w][\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
:

Consequently, ![]() admits the factorization
admits the factorization ![]() in
in ![]() .
.
Proof By Theorems 4.1 and 6.7 of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17] and Theorem 3.8 above,
![]() $\mathcal {R}(z)$
and
$\mathcal {R}(z)$
and
![]() $\mathcal {R}^\chi (z)$
satisfy
$\mathcal {R}^\chi (z)$
satisfy
![]() $ (\tau _w\otimes \mathbf {1})\mathcal {R}(z)=\mathcal {R}(w+z)$
and
$ (\tau _w\otimes \mathbf {1})\mathcal {R}(z)=\mathcal {R}(w+z)$
and
![]() $(\tau _w\otimes \mathbf {1} )\mathcal {R}^\chi (z)=\mathcal {R}^\chi (w+z) $
in
$(\tau _w\otimes \mathbf {1} )\mathcal {R}^\chi (z)=\mathcal {R}^\chi (w+z) $
in
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes 2}[w][\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
, for each choice of the symbol
$Y_{\hbar }(\mathfrak {g})^{\otimes 2}[w][\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
, for each choice of the symbol
![]() $\chi $
. Therefore, to prove the first assertion of the theorem, it is sufficient to establish the equalities
$\chi $
. Therefore, to prove the first assertion of the theorem, it is sufficient to establish the equalities
in
![]() $({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\otimes Y_{\hbar }\mathfrak {g})[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
and
$({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\otimes Y_{\hbar }\mathfrak {g})[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
and ![]() , respectively. These relations will hold provided their images under the evaluations
, respectively. These relations will hold provided their images under the evaluations

are satisfied in
![]() $Y_{\hbar }\mathfrak {g}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
for each
$Y_{\hbar }\mathfrak {g}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
for each
![]() $f\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
and
$f\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
and
![]() $f^\chi \in {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
, respectively. This follows from the definition of
$f^\chi \in {\dot {\mathsf {Y}}}_{\hbar }^{\chi }\mathfrak {g}{\vphantom {)}}^\star $
, respectively. This follows from the definition of ![]() , (R1), and Corollary 7.7, which collectively output the relations
, (R1), and Corollary 7.7, which collectively output the relations

This completes the proof of the first statement of the theorem. The second assertion now follows immediately from the decomposition
![]() $\mathcal {R}(z)=\mathcal {R}^+(z)\mathcal {R}^0(z)\mathcal {R}^-(z)$
(see Theorem 3.8) and the injectivity of
$\mathcal {R}(z)=\mathcal {R}^+(z)\mathcal {R}^0(z)\mathcal {R}^-(z)$
(see Theorem 3.8) and the injectivity of ![]() .
.
Remark 9.7 In the closely related setting of [Reference Khoroshkin and Tolstoy32], a formal version (i.e., suppressing convergence issues) of the factorization ![]() from Theorem 9.6 was established in [Reference Khoroshkin and Tolstoy32, Proposition 5.1] by proving directly that the Hopf pairing between the Yangian and its dual splits with respect to the underlying triangular decompositions (see Theorem 3.1 therein).
from Theorem 9.6 was established in [Reference Khoroshkin and Tolstoy32, Proposition 5.1] by proving directly that the Hopf pairing between the Yangian and its dual splits with respect to the underlying triangular decompositions (see Theorem 3.1 therein).
Remark 9.8 Since
![]() $\Phi _z$
intertwines the Chevalley involutions of
$\Phi _z$
intertwines the Chevalley involutions of
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
and
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
and
![]() $Y_{\hbar }\mathfrak {g}$
, it follows from Part (2) of Proposition 7.1 and the relation
$Y_{\hbar }\mathfrak {g}$
, it follows from Part (2) of Proposition 7.1 and the relation ![]() of Lemma 7.4 that
of Lemma 7.4 that
![]() $\check {\imath }$
satisfies
$\check {\imath }$
satisfies
![]() $\omega \circ \check {\imath }=\check {\imath }\circ \omega ^t$
. Consequently, the property (R2) translates to
$\omega \circ \check {\imath }=\check {\imath }\circ \omega ^t$
. Consequently, the property (R2) translates to
Hence, by Theorem 9.6,
![]() $\mathcal {R}(z)$
and its components
$\mathcal {R}(z)$
and its components
![]() $\mathcal {R}^\pm (z)$
satisfy the relations
$\mathcal {R}^\pm (z)$
satisfy the relations
In particular, this observation recovers the first identity of Corollary 3.10.
One can now interpret the quasitriangularity relations for
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
in terms of the relations of Theorem 3.8. Namely, setting
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
in terms of the relations of Theorem 3.8. Namely, setting
![]() $v=w-z$
, we see that the cabling identities of
$v=w-z$
, we see that the cabling identities of ![]() correspond to the relations
correspond to the relations
 $$ \begin{align*} \Delta\otimes \mathbf{1} (\mathcal{R}(v))&= \mathcal{R}_{13}(v)\mathcal{R}_{23}(v),\\ \mathbf{1}\otimes \Delta (\mathcal{R}(v))&= \mathcal{R}_{13}(v)\mathcal{R}_{12}(v) \end{align*} $$
$$ \begin{align*} \Delta\otimes \mathbf{1} (\mathcal{R}(v))&= \mathcal{R}_{13}(v)\mathcal{R}_{23}(v),\\ \mathbf{1}\otimes \Delta (\mathcal{R}(v))&= \mathcal{R}_{13}(v)\mathcal{R}_{12}(v) \end{align*} $$
in
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes 3}[w][\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
, which are satisfied by Theorem 3.8. In more detail, these are obtained heuristically by applying
$Y_{\hbar }(\mathfrak {g})^{\otimes 3}[w][\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
, which are satisfied by Theorem 3.8. In more detail, these are obtained heuristically by applying
![]() $\Phi _u\otimes \Phi _w\otimes \Phi _z$
and
$\Phi _u\otimes \Phi _w\otimes \Phi _z$
and
![]() $\Phi _w\otimes \Phi _y\otimes \Phi _z$
to
$\Phi _w\otimes \Phi _y\otimes \Phi _z$
to
respectively, where
![]() $\dot \Delta $
is the coproduct on
$\dot \Delta $
is the coproduct on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
, and then evaluating
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
, and then evaluating
![]() $u\mapsto w$
and
$u\mapsto w$
and
![]() $y\mapsto z$
while using
$y\mapsto z$
while using
![]() $(\Phi _u\otimes \Phi _z) \circ \dot \Delta |_{u=z} = \dot \Delta \circ \Phi _z $
. Similarly, applying
$(\Phi _u\otimes \Phi _z) \circ \dot \Delta |_{u=z} = \dot \Delta \circ \Phi _z $
. Similarly, applying
![]() $\Phi _w\otimes \Phi _z$
to the intertwiner equation
$\Phi _w\otimes \Phi _z$
to the intertwiner equation ![]() for
for
![]() $x\in Y_{\hbar }(\mathfrak {g})$
leads to the identity
$x\in Y_{\hbar }(\mathfrak {g})$
leads to the identity
in
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes 2}[w][z;z^{-1}]\!\kern-1.2pt]$
, which is satisfied by Theorem 3.8. We caution, however, that the situation here is more subtle for general
$Y_{\hbar }(\mathfrak {g})^{\otimes 2}[w][z;z^{-1}]\!\kern-1.2pt]$
, which is satisfied by Theorem 3.8. We caution, however, that the situation here is more subtle for general
![]() $x\in \mathrm {D}Y_{\hbar }\mathfrak {g}$
.
$x\in \mathrm {D}Y_{\hbar }\mathfrak {g}$
.
9.4 Remarks
The identifications established in Theorem 9.6 provide a rigorous framework for understanding the motivating remarks given in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Section 1.6]. We now give a few comments related to this point.
First, we note that the diagonal factor
![]() $\mathcal {R}^0(z)$
of
$\mathcal {R}^0(z)$
of
![]() $\mathcal {R}(z)$
was explicitly obtained in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Section 6.6] by computing the common asymptotic expansion of the two
$\mathcal {R}(z)$
was explicitly obtained in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Section 6.6] by computing the common asymptotic expansion of the two
![]() $\mathrm {GL}(V_1\otimes V_2)$
-valued meromorphic abelian R-matrices constructed in [Reference Gautam and Toledano Laredo16, Section 5], where
$\mathrm {GL}(V_1\otimes V_2)$
-valued meromorphic abelian R-matrices constructed in [Reference Gautam and Toledano Laredo16, Section 5], where
![]() $V_1,V_2$
are an arbitrary pair of finite-dimensional representations of the Yangian. As explained in [Reference Gautam and Toledano Laredo16, Section 5.2], their construction was motivated by the heuristic formula for
$V_1,V_2$
are an arbitrary pair of finite-dimensional representations of the Yangian. As explained in [Reference Gautam and Toledano Laredo16, Section 5.2], their construction was motivated by the heuristic formula for ![]() given in [Reference Khoroshkin and Tolstoy32, Theorem 5.2]. Theorem 9.6 makes this relation precise, and shows that the explicit formula for
given in [Reference Khoroshkin and Tolstoy32, Theorem 5.2]. Theorem 9.6 makes this relation precise, and shows that the explicit formula for
![]() $\mathcal {R}^0(z)$
obtained in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17], and recalled in Section 3.6, does indeed compute the canonical element defined by the pairing on
$\mathcal {R}^0(z)$
obtained in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17], and recalled in Section 3.6, does indeed compute the canonical element defined by the pairing on
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}\times {\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
.
${\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}\times {\dot {\mathsf {Y}}}_{\hbar }^{0}\mathfrak {g}{\vphantom {)}}^\star $
.
Next, we emphasize that the factor ![]() (equivalently,
(equivalently,
![]() $\mathcal {R}^\pm (z)$
) now admits two distinct characterizations. On the one hand, it is uniquely determined by the recurrence relations (3.18) which were at the heart of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Theorem 4.1]. On the other hand, it arises as the canonical element defined by the pairing on
$\mathcal {R}^\pm (z)$
) now admits two distinct characterizations. On the one hand, it is uniquely determined by the recurrence relations (3.18) which were at the heart of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Theorem 4.1]. On the other hand, it arises as the canonical element defined by the pairing on
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}\times {\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
, and can thus be realized explicitly by computing the dual set to any fixed homogeneous basis of the
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}\times {\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
, and can thus be realized explicitly by computing the dual set to any fixed homogeneous basis of the
![]() $\mathbb {N}$
-graded torsion free
$\mathbb {N}$
-graded torsion free
![]() $\mathbb {C}[{\hbar }]$
-module
$\mathbb {C}[{\hbar }]$
-module
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})$
. In more detail, if
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})$
. In more detail, if
![]() $\mathsf {B}^\pm _k\subset {\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})_k$
is a lift of any basis of the finite-dimensional kth component
$\mathsf {B}^\pm _k\subset {\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})_k$
is a lift of any basis of the finite-dimensional kth component
![]() $\mathsf {S}_k({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}^\pm )$
of
$\mathsf {S}_k({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}^\pm )$
of
![]() $\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}^\pm )\cong {\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})/{\hbar }{\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})$
(see Section 5.3), then
$\mathsf {S}({\hbar }{\mathfrak {t}}_{\scriptscriptstyle {+}}^\pm )\cong {\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})/{\hbar }{\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})$
(see Section 5.3), then
![]() $\mathsf {B}^\pm =\bigcup _k\mathsf {B}^\pm _k$
is a basis of
$\mathsf {B}^\pm =\bigcup _k\mathsf {B}^\pm _k$
is a basis of
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})$
and
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})$
and
where
![]() $\{f_x\}_{x\in \mathsf {B}^\pm }\subset {\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
is the dual set to
$\{f_x\}_{x\in \mathsf {B}^\pm }\subset {\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
is the dual set to
![]() $\mathsf {B}^\pm $
, uniquely determined by
$\mathsf {B}^\pm $
, uniquely determined by
![]() $f_x(y)=\delta _{xy}$
for all
$f_x(y)=\delta _{xy}$
for all
![]() $x,y \in \mathsf {B}^\pm $
. Here, we note if x is of degree k, then it follows automatically that
$x,y \in \mathsf {B}^\pm $
. Here, we note if x is of degree k, then it follows automatically that
![]() $f_x\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{-k}\cong \mathrm {Hom}_{\mathbb {C}[{\hbar }]}^{-k}({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}),\mathbb {C}[{\hbar }])$
. This implies that the right-hand side of the above expression defines a unique element in
$f_x\in {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{-k}\cong \mathrm {Hom}_{\mathbb {C}[{\hbar }]}^{-k}({\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g}),\mathbb {C}[{\hbar }])$
. This implies that the right-hand side of the above expression defines a unique element in ![]() , which coincides with
, which coincides with ![]() as its image under
as its image under
![]() $\Theta _\pm \circ (\imath \,\dot {\otimes }\,\check {\imath })^{-1}$
is
$\Theta _\pm \circ (\imath \,\dot {\otimes }\,\check {\imath })^{-1}$
is
![]() $\mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}}$
(see (9.5) and Section 9.3).
$\mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}}$
(see (9.5) and Section 9.3).
In the special case where
![]() $\mathfrak {g}=\mathfrak {s}\mathfrak {l}_2$
, there are two closed-form expressions for
$\mathfrak {g}=\mathfrak {s}\mathfrak {l}_2$
, there are two closed-form expressions for ![]() (equivalently,
(equivalently,
![]() $\mathcal {R}^\pm (z)$
) which have arisen from these two separate viewpoints (see [Reference Khoroshkin and Tolstoy32, Theorem 5.1] and [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Theorem 5.5]). For
$\mathcal {R}^\pm (z)$
) which have arisen from these two separate viewpoints (see [Reference Khoroshkin and Tolstoy32, Theorem 5.1] and [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Theorem 5.5]). For
![]() $\mathfrak {g}$
of arbitrary rank, no such expressions are known, though an infinite-product formula for
$\mathfrak {g}$
of arbitrary rank, no such expressions are known, though an infinite-product formula for ![]() was conjectured in [Reference Khoroshkin and Tolstoy32, (5.43)], motivated by the earlier works [Reference Khoroshkin, Stolin and Tolstoy28–Reference Khoroshkin, Tolstoy, Doebner, Dobrev and Ushveridze31].
was conjectured in [Reference Khoroshkin and Tolstoy32, (5.43)], motivated by the earlier works [Reference Khoroshkin, Stolin and Tolstoy28–Reference Khoroshkin, Tolstoy, Doebner, Dobrev and Ushveridze31].
9.5 On the blocks of 
To conclude, we wish to highlight that the dual bases approach discussed in the previous subsection provides a natural interpretation of some of the basic properties of
![]() $\mathcal {R}^\pm (z)$
discovered in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17].
$\mathcal {R}^\pm (z)$
discovered in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17].
Given
![]() $\beta \in Q$
, let
$\beta \in Q$
, let
![]() $\pi _\beta :\mathrm {D}Y_{\hbar }\mathfrak {g}\to \mathrm {D}Y_{\hbar }{\mathfrak {g}}_\beta $
denote the
$\pi _\beta :\mathrm {D}Y_{\hbar }\mathfrak {g}\to \mathrm {D}Y_{\hbar }{\mathfrak {g}}_\beta $
denote the
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear projection associated with the topological Q-grading on
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-linear projection associated with the topological Q-grading on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
defined in Section 4.2, and let
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
defined in Section 4.2, and let
![]() ${\dot \pi _\beta :{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\twoheadrightarrow {\dot {\mathsf {Y}}}_{\hbar }{\mathfrak {g}}_\beta} $
denote its restriction to
${\dot \pi _\beta :{\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}\twoheadrightarrow {\dot {\mathsf {Y}}}_{\hbar }{\mathfrak {g}}_\beta} $
denote its restriction to
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
. Consider the element
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}$
. Consider the element
where we view
![]() $\mathrm {End}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g})\subset \mathrm {End}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g})$
, as in Section 9.2. Note that under the identification provided by the natural inclusion
$\mathrm {End}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g})\subset \mathrm {End}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g})$
, as in Section 9.2. Note that under the identification provided by the natural inclusion
it coincides with the identity transformation of
![]() $\mathrm {End}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }^{\pm }{\mathfrak {g}}_\beta )$
. For each
$\mathrm {End}_{\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]}({\dot {\mathsf {Y}}}_{\hbar }^{\pm }{\mathfrak {g}}_\beta )$
. For each
![]() $\beta \in Q_+$
, we may therefore define
$\beta \in Q_+$
, we may therefore define
![]() $R_\beta ^\pm :=\Theta ^{-1}(\mathbf {1}_\beta ^\pm )$
, where
$R_\beta ^\pm :=\Theta ^{-1}(\mathbf {1}_\beta ^\pm )$
, where
![]() $\mathbf {1}_\beta ^\pm =\mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }^{\pm }{\mathfrak {g}}_{\pm \beta }}$
. By (9.4) and the reasoning used in (R2) of Section 9.3, we have
$\mathbf {1}_\beta ^\pm =\mathbf {1}_{{\dot {\mathsf {Y}}}_{\hbar }^{\pm }{\mathfrak {g}}_{\pm \beta }}$
. By (9.4) and the reasoning used in (R2) of Section 9.3, we have
where we note that, for each
![]() $\alpha \in Q$
,
$\alpha \in Q$
,
![]() $\dot {\pi }_\alpha ^t$
is just the projection
$\dot {\pi }_\alpha ^t$
is just the projection
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \twoheadrightarrow {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{-\alpha }$
associated with the topological Q-grading on
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star \twoheadrightarrow {\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star _{-\alpha }$
associated with the topological Q-grading on
![]() ${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
(see Corollary 6.5). In the topological tensor product
${\dot {\mathsf {Y}}}_{\hbar }\mathfrak {g}{\vphantom {)}}^\star $
(see Corollary 6.5). In the topological tensor product
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}\,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
, we have the equality
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}\,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
, we have the equality
![]() $R^\pm =\sum _{\beta \in Q_+}R_\beta ^\pm $
.
$R^\pm =\sum _{\beta \in Q_+}R_\beta ^\pm $
.
For the sake of the below discussion, it is worth pointing out that the convergence of the infinite sum
![]() $\sum _{\beta \in Q_+}R_\beta ^\pm $
is also clear from the point of view of dual bases. Indeed, by Corollary 5.5, we have
$\sum _{\beta \in Q_+}R_\beta ^\pm $
is also clear from the point of view of dual bases. Indeed, by Corollary 5.5, we have
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})_{\pm \beta }\subset {\hbar }^{\nu (\beta )}Y_{\hbar }^\pm (\mathfrak {g})_{\pm \beta }$
, where we recall that
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})_{\pm \beta }\subset {\hbar }^{\nu (\beta )}Y_{\hbar }^\pm (\mathfrak {g})_{\pm \beta }$
, where we recall that
![]() $\nu (\beta )\in \mathbb {N}$
is defined by (3.17). Hence, any homogeneous element in
$\nu (\beta )\in \mathbb {N}$
is defined by (3.17). Hence, any homogeneous element in
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})_{\pm \beta }$
with respect to the underlying
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})_{\pm \beta }$
with respect to the underlying
![]() $\mathbb {N}$
-grading belongs to
$\mathbb {N}$
-grading belongs to
![]() ${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})_{\nu (\beta )+\ell }$
for some
${\dot {\mathsf {Y}}}_{\hbar }(\mathfrak {g})_{\nu (\beta )+\ell }$
for some
![]() $\ell \in \mathbb {N}$
. It follows that the dual set to any homogeneous basis of the
$\ell \in \mathbb {N}$
. It follows that the dual set to any homogeneous basis of the
![]() $\mathbb {N}$
-graded
$\mathbb {N}$
-graded
![]() $\mathbb {C}[{\hbar }]$
-module
$\mathbb {C}[{\hbar }]$
-module
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})_{\pm \beta }$
belongs to
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})_{\pm \beta }$
belongs to
where the space on the right-hand side is the closure of the
![]() $\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module generated by the left-hand side (see Section 9.2). This implies the convergence of
$\mathbb {C}[\kern-1.2pt\![{\hbar }]\!\kern-1.2pt]$
-module generated by the left-hand side (see Section 9.2). This implies the convergence of
![]() $\sum _{\beta \in Q_+}R_\beta ^\pm $
in
$\sum _{\beta \in Q_+}R_\beta ^\pm $
in
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}\,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
while establishing that
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}\,\widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
while establishing that
![]() $R_\beta ^\pm \in {\hbar }^{\nu (\beta )} Y_{\hbar }^{\pm \!}\mathfrak {g}\, \widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
. Next, following the procedure from Section 9.3, let us set
$R_\beta ^\pm \in {\hbar }^{\nu (\beta )} Y_{\hbar }^{\pm \!}\mathfrak {g}\, \widetilde {\otimes }\, {\dot {\mathsf {Y}}}_{\hbar }^{\pm }\mathfrak {g}{\vphantom {)}}^\star $
. Next, following the procedure from Section 9.3, let us set
The relations of (9.6) then translate to
where
![]() $\omega $
is the Chevalley involution on
$\omega $
is the Chevalley involution on
![]() $\mathrm {D}Y_{\hbar }\mathfrak {g}$
(see Section 4.2). Now recall that
$\mathrm {D}Y_{\hbar }\mathfrak {g}$
(see Section 4.2). Now recall that
![]() $\mathcal {R}_{\beta }^-(z)$
is the
$\mathcal {R}_{\beta }^-(z)$
is the
![]() $Y_{\hbar }(\mathfrak {g})_{-\beta }\otimes Y_{\hbar }(\mathfrak {g})_\beta $
component of
$Y_{\hbar }(\mathfrak {g})_{-\beta }\otimes Y_{\hbar }(\mathfrak {g})_\beta $
component of
![]() $\mathcal {R}^-(z)$
, characterized by the recurrence relation (3.18). The
$\mathcal {R}^-(z)$
, characterized by the recurrence relation (3.18). The
![]() $Y_{\hbar }(\mathfrak {g})_{\beta }\otimes Y_{\hbar }(\mathfrak {g})_{-\beta }$
block of
$Y_{\hbar }(\mathfrak {g})_{\beta }\otimes Y_{\hbar }(\mathfrak {g})_{-\beta }$
block of
![]() $\mathcal {R}^+(z)$
is then
$\mathcal {R}^+(z)$
is then
and we have the following corollary of Theorem 9.6.
Corollary 9.9 For each
![]() $\beta \in Q_+$
, the element
$\beta \in Q_+$
, the element ![]() satisfies
satisfies
in addition to the relation ![]() .
.
Of course, the second assertion is immediate from Theorem 9.6 as
![]() $\Phi _w$
is the identity on
$\Phi _w$
is the identity on
![]() $\mathfrak {g}$
and thus satisfies
$\mathfrak {g}$
and thus satisfies
![]() $\pi _\alpha \circ \Phi _w = \Phi _w\circ {\pi _\alpha }|_{Y_{\hbar }\mathfrak {g}}$
for all
$\pi _\alpha \circ \Phi _w = \Phi _w\circ {\pi _\alpha }|_{Y_{\hbar }\mathfrak {g}}$
for all
![]() $\alpha \in Q$
. The first statement then follows from the properties of
$\alpha \in Q$
. The first statement then follows from the properties of
![]() $\mathcal {R}^-(z)$
established in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17] and recalled in Section 3.6. However, we wish to point out that this assertion is a natural consequence of the above discussion on dual bases. Indeed, we have seen that any homogeneous basis of
$\mathcal {R}^-(z)$
established in [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17] and recalled in Section 3.6. However, we wish to point out that this assertion is a natural consequence of the above discussion on dual bases. Indeed, we have seen that any homogeneous basis of
![]() ${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})_\beta $
lies in
${\dot {\mathsf {Y}}}_{\hbar }^{\pm }(\mathfrak {g})_\beta $
lies in
![]() ${\hbar }^{\nu (\beta )}Y_{\hbar }(\mathfrak {g})$
, and that the image of its dual set under
${\hbar }^{\nu (\beta )}Y_{\hbar }(\mathfrak {g})$
, and that the image of its dual set under
![]() $\check {\imath }$
is contained in
$\check {\imath }$
is contained in
![]() $\bigoplus _{k\geq \nu (\beta )}\mathrm {D}Y_{\hbar }{\mathfrak {g}}_{-k}$
. As
$\bigoplus _{k\geq \nu (\beta )}\mathrm {D}Y_{\hbar }{\mathfrak {g}}_{-k}$
. As
![]() $\Phi _z$
is graded, we have
$\Phi _z$
is graded, we have
which yields the first statement of the corollary.
A Homogenization of the R-matrix
In this appendix, we show that the results of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Section 7.4] imply Theorem 3.8, as promised in Remark 3.9. Let
![]() $Y(\mathfrak {g})$
denote the Yangian defined over
$Y(\mathfrak {g})$
denote the Yangian defined over
![]() $\mathbb {C}$
with
$\mathbb {C}$
with
![]() ${\hbar }$
specialized to
${\hbar }$
specialized to
![]() $1$
:
$1$
:
Slightly abusing notation, we shall denote the images of
![]() $x_{ir}^\pm $
and
$x_{ir}^\pm $
and
![]() $h_{ir}$
again by
$h_{ir}$
again by
![]() $x_{ir}^\pm $
and
$x_{ir}^\pm $
and
![]() $h_{ir}$
, respectively. The graded Hopf algebra structure on
$h_{ir}$
, respectively. The graded Hopf algebra structure on
![]() $Y_{\hbar }(\mathfrak {g})$
induces on
$Y_{\hbar }(\mathfrak {g})$
induces on
![]() $Y(\mathfrak {g})$
the structure of an
$Y(\mathfrak {g})$
the structure of an
![]() $\mathbb {N}$
-filtered Hopf algebra over the complex numbers with filtration
$\mathbb {N}$
-filtered Hopf algebra over the complex numbers with filtration
![]() ${ {F}}_\bullet $
defined by letting
${ {F}}_\bullet $
defined by letting
![]() ${ {F}}_k$
denote the image of
${ {F}}_k$
denote the image of
![]() $\bigoplus _{n\leq k}Y_{\hbar }(\mathfrak {g})_k$
. The Yangian
$\bigoplus _{n\leq k}Y_{\hbar }(\mathfrak {g})_k$
. The Yangian
![]() $Y(\mathfrak {g})$
is then a filtered deformation of the graded Hopf algebra
$Y(\mathfrak {g})$
is then a filtered deformation of the graded Hopf algebra
![]() $U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
:
$U({\mathfrak {t}}_{\scriptscriptstyle {+}})$
:
One can recover
![]() $Y_{\hbar }(\mathfrak {g})$
from
$Y_{\hbar }(\mathfrak {g})$
from
![]() $Y(\mathfrak {g})$
using the Rees algebra formalism (see [Reference Guay, Regelskis and Wendlandt22, Proposition 2.2] and [Reference Guay, Regelskis and Wendlandt23, Theorem 6.10], for example). In more detail, there is an isomorphism of
$Y(\mathfrak {g})$
using the Rees algebra formalism (see [Reference Guay, Regelskis and Wendlandt22, Proposition 2.2] and [Reference Guay, Regelskis and Wendlandt23, Theorem 6.10], for example). In more detail, there is an isomorphism of
![]() $\mathbb {N}$
-graded Hopf algebras
$\mathbb {N}$
-graded Hopf algebras

Here, the Hopf algebra structure on
![]() $\mathsf {R}_{\hbar }(Y(\mathfrak {g}))$
is obtained by extending that of
$\mathsf {R}_{\hbar }(Y(\mathfrak {g}))$
is obtained by extending that of
![]() $Y(\mathfrak {g})$
by
$Y(\mathfrak {g})$
by
![]() $\mathbb {C}[{\hbar }]$
-linearity, and we note that
$\mathbb {C}[{\hbar }]$
-linearity, and we note that
![]() $\mathsf {R}_{\hbar }(Y(\mathfrak {g})\otimes _{\mathbb {C}} Y(\mathfrak {g}))\cong \mathsf {R}_{\hbar }(Y(\mathfrak {g}))\otimes _{\mathbb {C}[{\hbar }]} \mathsf {R}_{\hbar }(Y(\mathfrak {g}))$
.
$\mathsf {R}_{\hbar }(Y(\mathfrak {g})\otimes _{\mathbb {C}} Y(\mathfrak {g}))\cong \mathsf {R}_{\hbar }(Y(\mathfrak {g}))\otimes _{\mathbb {C}[{\hbar }]} \mathsf {R}_{\hbar }(Y(\mathfrak {g}))$
.
In [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17], the universal R-matrix
![]() $ {R}(z)$
of the Yangian
$ {R}(z)$
of the Yangian
![]() $Y(\mathfrak {g})$
is constructed as a product
$Y(\mathfrak {g})$
is constructed as a product
where
![]() $ {R}^+(z)= {R}^-_{21}(-z)^{-1}$
and the factors
$ {R}^+(z)= {R}^-_{21}(-z)^{-1}$
and the factors
![]() $ {R}^-(z)$
and
$ {R}^-(z)$
and
![]() $ {R}^0(z)$
are as in Sections 4.1 and 6.6 of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17], respectively. In particular,
$ {R}^0(z)$
are as in Sections 4.1 and 6.6 of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17], respectively. In particular,
![]() $ {R}^\pm (z)-1$
,
$ {R}^\pm (z)-1$
,
![]() $ {R}^0(z)-1$
, and
$ {R}^0(z)-1$
, and
![]() $ {R}(z)-1$
lay in the subspace
$ {R}(z)-1$
lay in the subspace
and hence
![]() $ {R}^{\pm }(z/{\hbar })$
,
$ {R}^{\pm }(z/{\hbar })$
,
![]() $ {R}^0(z/{\hbar })$
, and
$ {R}^0(z/{\hbar })$
, and
![]() $ {R}(z/{\hbar })$
are elements of
$ {R}(z/{\hbar })$
are elements of
![]() $\mathsf {R}_{\hbar }(Y(\mathfrak {g}))^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. The definitions of
$\mathsf {R}_{\hbar }(Y(\mathfrak {g}))^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. The definitions of
![]() $\mathcal {R}^\pm (z)$
,
$\mathcal {R}^\pm (z)$
,
![]() $\mathcal {R}^0(z)$
and
$\mathcal {R}^0(z)$
and
![]() $\mathcal {R}(z)$
given in Section 3.6 are such that one has the equalities
$\mathcal {R}(z)$
given in Section 3.6 are such that one has the equalities

Using this fact and the results of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17], we can recover the below proposition, which is a restatement of Theorem 3.8.
Proposition A.1
![]() $\mathcal {R}(z)$
is the unique formal series in
$\mathcal {R}(z)$
is the unique formal series in
![]() $ 1+z^{-1}Y_{\hbar }(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt] $
satisfying the intertwiner equation
$ 1+z^{-1}Y_{\hbar }(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt] $
satisfying the intertwiner equation
in
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes 2}[z;z^{-1}]\!\kern-1.2pt]$
, in addition to the cabling identities
$Y_{\hbar }(\mathfrak {g})^{\otimes 2}[z;z^{-1}]\!\kern-1.2pt]$
, in addition to the cabling identities
 $$ \begin{align*} \Delta\otimes \mathbf{1} (\mathcal{R}(z))&= \mathcal{R}_{13}(z)\mathcal{R}_{23}(z),\\ \mathbf{1}\otimes \Delta (\mathcal{R}(z))&= \mathcal{R}_{13}(z)\mathcal{R}_{12}(z) \end{align*} $$
$$ \begin{align*} \Delta\otimes \mathbf{1} (\mathcal{R}(z))&= \mathcal{R}_{13}(z)\mathcal{R}_{23}(z),\\ \mathbf{1}\otimes \Delta (\mathcal{R}(z))&= \mathcal{R}_{13}(z)\mathcal{R}_{12}(z) \end{align*} $$
in
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes 3}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. Moreover,
$Y_{\hbar }(\mathfrak {g})^{\otimes 3}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. Moreover,
![]() $\mathcal {R}(z)$
satisfies the properties (1)–(3) of Theorem 3.8.
$\mathcal {R}(z)$
satisfies the properties (1)–(3) of Theorem 3.8.
Proof That
![]() $\mathcal {R}(z)$
satisfies the properties (1)–(3) of Theorem 3.8 follows from (A.1) and the corresponding properties of
$\mathcal {R}(z)$
satisfies the properties (1)–(3) of Theorem 3.8 follows from (A.1) and the corresponding properties of
![]() $ {R}(z)$
established in (3)–(5) of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Theorem 7.4]. Similarly, that
$ {R}(z)$
established in (3)–(5) of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Theorem 7.4]. Similarly, that
![]() $\mathcal {R}(z)$
satisfies the cabling identities in
$\mathcal {R}(z)$
satisfies the cabling identities in
![]() $Y_{\hbar }(\mathfrak {g})^{\otimes 3}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
follows from the equality
$Y_{\hbar }(\mathfrak {g})^{\otimes 3}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
follows from the equality ![]() and Theorem 7.4(2) of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17], which asserts that
and Theorem 7.4(2) of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17], which asserts that
![]() $ {R}(z)$
satisfies the cabling identities in
$ {R}(z)$
satisfies the cabling identities in
![]() $Y(\mathfrak {g})^{\otimes 3}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. As for the intertwiner equation, upon applying the isomorphism
$Y(\mathfrak {g})^{\otimes 3}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
. As for the intertwiner equation, upon applying the isomorphism ![]() , we deduce that it will hold provided
, we deduce that it will hold provided
![]() $ {R}(z)$
satisfies
$ {R}(z)$
satisfies
in
![]() $\mathsf {R}_{\hbar }(Y(\mathfrak {g}))^{\otimes 2}[z;z^{-1}]\!\kern-1.2pt]\subset (Y(\mathfrak {g})^{\otimes 2})[{\hbar }][z;z^{-1}]\!\kern-1.2pt]$
, where
$\mathsf {R}_{\hbar }(Y(\mathfrak {g}))^{\otimes 2}[z;z^{-1}]\!\kern-1.2pt]\subset (Y(\mathfrak {g})^{\otimes 2})[{\hbar }][z;z^{-1}]\!\kern-1.2pt]$
, where ![]() . Since
. Since ![]() is determined by
is determined by
the above equality will hold provided that, for each
![]() $x\in Y(\mathfrak {g})$
, and
$x\in Y(\mathfrak {g})$
, and
![]() $\zeta \in \mathbb {C}^\times $
, one has
$\zeta \in \mathbb {C}^\times $
, one has
where
![]() $\mathring {\tau }_z:Y(\mathfrak {g})\to Y(\mathfrak {g})[z]$
is obtained by specializing the algebra homomorphism
$\mathring {\tau }_z:Y(\mathfrak {g})\to Y(\mathfrak {g})[z]$
is obtained by specializing the algebra homomorphism
![]() $\tau _z$
defined in (3.8). This equality is immediate from Part (1) of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Theorem 7.4].
$\tau _z$
defined in (3.8). This equality is immediate from Part (1) of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17, Theorem 7.4].
As for the uniqueness assertion; the argument given in Appendix B of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17] translates naturally to the formal setting. Alternatively, one can see this as a consequence of the uniqueness of
![]() $ {R}(z)$
itself, as proven therein. Indeed, if
$ {R}(z)$
itself, as proven therein. Indeed, if
![]() $\mathscr {R}(z)\in 1+z^{-1}Y_{\hbar }(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
is another solution of the intertwiner equation satisfying the cabling identities, then to see that
$\mathscr {R}(z)\in 1+z^{-1}Y_{\hbar }(\mathfrak {g})^{\otimes 2}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
is another solution of the intertwiner equation satisfying the cabling identities, then to see that
![]() $\mathscr {R}(z)=\mathcal {R}(z)$
, it suffices to show that
$\mathscr {R}(z)=\mathcal {R}(z)$
, it suffices to show that
![]() $ {X}(z)|_{{\hbar }=\zeta }= {R}(z/\zeta )$
for each
$ {X}(z)|_{{\hbar }=\zeta }= {R}(z/\zeta )$
for each
![]() $\zeta \in \mathbb {C}^\times $
, where
$\zeta \in \mathbb {C}^\times $
, where
This follows from the fact that
![]() $ {X}(z)|_{{\hbar }=\zeta }$
and
$ {X}(z)|_{{\hbar }=\zeta }$
and
![]() $ {R}(z/\zeta )$
both satisfy the cabling identities in
$ {R}(z/\zeta )$
both satisfy the cabling identities in
![]() $Y(\mathfrak {g})^{\otimes 3}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
and the intertwiner equation (A.2), and so coincide by the uniqueness of
$Y(\mathfrak {g})^{\otimes 3}[\kern-1.2pt\![z^{-1}]\!\kern-1.2pt]$
and the intertwiner equation (A.2), and so coincide by the uniqueness of
![]() $ {R}(z)$
, as established in Appendix B of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17].
$ {R}(z)$
, as established in Appendix B of [Reference Gautam, Toledano Laredo, Wendlandt, Alekseev, Frenkel, Rosso, Webster and Yakimov17].
Acknowledgments
I would like to thank Alex Weekes, Andrea Appel, Sachin Gautam, and Valerio Toledano Laredo for the many insightful discussions and helpful comments they have been the source of over the last few years. These have played a significant role in shaping this article.