There are many computational problems which are generally “easy” to solve but have certain rare examples which are much more difficult to solve. One approach to studying these problems is to ignore the difficult edge cases. Asymptotic computability is one of the formal tools that uses this approach to study these problems. Asymptotically computable sets can be thought of as almost computable sets, however every set is computationally equivalent to an almost computable set. Intrinsic density was introduced as a way to get around this unsettling fact, and which will be our main focus.
Of particular interest for the first half of this dissertation are the intrinsically small sets, the sets of intrinsic density 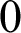 $0$
. While the bulk of the existing work concerning intrinsic density was focused on these sets, there were still many questions left unanswered. The first half of this dissertation answers some of these questions. We proved some useful closure properties for the intrinsically small sets and applied them to prove separations for the intrinsic variants of asymptotic computability. We also completely separated hyperimmunity and intrinsic smallness in the Turing degrees and resolved some open questions regarding the relativization of intrinsic density.
$0$
. While the bulk of the existing work concerning intrinsic density was focused on these sets, there were still many questions left unanswered. The first half of this dissertation answers some of these questions. We proved some useful closure properties for the intrinsically small sets and applied them to prove separations for the intrinsic variants of asymptotic computability. We also completely separated hyperimmunity and intrinsic smallness in the Turing degrees and resolved some open questions regarding the relativization of intrinsic density.
For the second half of this dissertation, we turned our attention to the study of intermediate intrinsic density. We developed a calculus using noncomputable coding operations to construct examples of sets with intermediate intrinsic density. For almost all 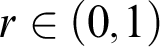 $r\in (0,1)$
, this construction yielded the first known example of a set with intrinsic density r which cannot compute a set random with respect to the r-Bernoulli measure. Motivated by the fact that intrinsic density coincides with the notion of injection stochasticity, we applied these techniques to study the structure of the more well-known notion of MWC-stochasticity.
$r\in (0,1)$
, this construction yielded the first known example of a set with intrinsic density r which cannot compute a set random with respect to the r-Bernoulli measure. Motivated by the fact that intrinsic density coincides with the notion of injection stochasticity, we applied these techniques to study the structure of the more well-known notion of MWC-stochasticity.
Abstract prepared by Justin Miller.
E-mail: jmille74@nd.edu
URL: https://curate.nd.edu/show/6t053f4938w
