Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Simpson, Stephen G.
2011.
Mass problems associated with effectively closed sets.
Tohoku Mathematical Journal,
Vol. 63,
Issue. 4,
Higuchi, Kojiro
and
Kihara, Takayuki
2012.
How the World Computes.
Vol. 7318,
Issue. ,
p.
303.
Higuchi, Kojiro
and
Kihara, Takayuki
2014.
On effectively closed sets of effective strong measure zero.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 9,
p.
1445.
Higuchi, Kojiro
Hudelson, W.M. Phillip
Simpson, Stephen G.
and
Yokoyama, Keita
2014.
Propagation of partial randomness.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 2,
p.
742.
Kihara, Takayuki
and
Miyabe, Kenshi
2015.
Unified characterizations of lowness properties via Kolmogorov complexity.
Archive for Mathematical Logic,
Vol. 54,
Issue. 3-4,
p.
329.
Hölzl, Rupert
and
Porter, Christopher P.
2017.
Randomness for computable measures and initial segment complexity.
Annals of Pure and Applied Logic,
Vol. 168,
Issue. 4,
p.
860.
Cenzer, Douglas
and
Porter, Christopher P.
2018.
The Random Members of a
Π
1
0
${\Pi }_{1}^{0}$
Class.
Theory of Computing Systems,
Vol. 62,
Issue. 7,
p.
1637.

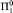 class
class 