Consider a stationary Markov chain 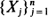with state space consisting of the ξ -letter alphabet set Λ= {a1, a2, ···, aξ }. We study the variables M=M(n, k) and N=N(n, k), defined, respectively, as the number of overlapping and non-overlapping occurrences of a fixed periodic k-letter word, and use the Stein–Chen method to obtain compound Poisson approximations for their distribution.

Let X1, X2, · ··, Xn be a sequence of n random variables taking values in the ξ -letter alphabet . We consider the number N = N(n, k) of non-overlapping occurrences of a fixed k-letter word under (a) i.i.d. and (b) stationary Markovian hypotheses on the sequence , and use the Stein–Chen method to obtain Poisson approximations for the same. In each case, results and couplings from Barbour et al. (1992) are used to show that the total variation distance between the distribution of N and that of an appropriate Poisson random variable is of order (roughly) O(kS(k)), where S(k) denotes the stationary probability of the word in question. These results vastly improve on the approximations obtained in Godbole (1991). In the Markov case, we also make use of recently obtained eigenvalue bounds on convergence to stationarity due to Diaconis and Stroock (1991) and Fill (1991).