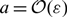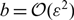Refine search
Actions for selected content:
9 results
Spikes and localised patterns for a novel Schnakenberg model in the semi-strong interaction regime
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 25 January 2021, pp. 133-152
-
- Article
- Export citation
On a model for phase separation on biological membranes and its relation to the Ohta–Kawasaki equation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 11 March 2019, pp. 297-338
-
- Article
- Export citation
A Meshfree Technique for Numerical Simulation of Reaction-Diffusion Systems in Developmental Biology
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 11 July 2017, pp. 1225-1249
- Print publication:
- October 2017
-
- Article
- Export citation
Projected Finite Elements for Systems of Reaction-Diffusion Equations on Closed Evolving Spheroidal Surfaces
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 07 February 2017, pp. 718-747
- Print publication:
- March 2017
-
- Article
- Export citation
Replicator Equations and Space
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 3 / 2014
- Published online by Cambridge University Press:
- 28 May 2014, pp. 47-67
- Print publication:
- 2014
-
- Article
- Export citation
Moving Finite Element Simulations for Reaction-Diffusion Systems
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 4 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 03 June 2015, pp. 365-381
- Print publication:
- June 2012
-
- Article
- Export citation
Dynamics of Erythroid Progenitors and Erythroleukemia
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 4 / Issue 3 / 2009
- Published online by Cambridge University Press:
- 05 June 2009, pp. 210-232
- Print publication:
- 2009
-
- Article
- Export citation
Travelling Waves in Partially DegenerateReaction-Diffusion Systems
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 2 / Issue 2 / 2007
- Published online by Cambridge University Press:
- 15 June 2008, pp. 106-125
- Print publication:
- 2007
-
- Article
- Export citation
Dynamics of Propagation Phenomena in Biological Pattern Formation
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 1 / Issue 1 / 2006
- Published online by Cambridge University Press:
- 15 May 2008, pp. 98-119
- Print publication:
- 2006
-
- Article
- Export citation