We use a special tiling for the hyperbolic d-space $\mathbb {H}^d$ for $d=2,3,4$ to construct an (almost) explicit isomorphism between the Lipschitz-free space $\mathcal {F}(\mathbb {H}^d)$ and $\mathcal {F}(P)\oplus \mathcal {F}(\mathcal {N})$, where P is a polytope in $\mathbb {R}^d$ and $\mathcal {N}$ a net in $\mathbb {H}^d$ coming from the tiling. This implies that the spaces $\mathcal {F}(\mathbb {H}^d)$ and $\mathcal {F}(\mathbb {R}^d)\oplus \mathcal {F}(\mathcal {M})$ are isomorphic for every net $\mathcal {M}$ in $\mathbb {H}^d$. In particular, we obtain that, for $d=2,3,4$, $\mathcal {F}(\mathbb {H}^d)$ has a Schauder basis. Moreover, using a similar method, we also give an explicit isomorphism between $\mathrm {Lip}(\mathbb {H}^d)$ and $\mathrm {Lip}(\mathbb {R}^d)$.

We consider the Cauchy problem for a general class of parabolic partial differential equations in the Euclidean space ℝN. We show that given a weighted Lp-space $L_w^p({\mathbb {R}}^N)$ with 1 ⩽ p < ∞ and a fast growing weight w, there is a Schauder basis $(e_n)_{n=1}^\infty$ in $L_w^p({\mathbb {R}}^N)$ with the following property: given an arbitrary positive integer m there exists nm > 0 such that, if the initial data f belongs to the closed linear span of en with n ⩾ nm, then the decay rate of the solution of the problem is at least t−m for large times t.

The result generalizes the recent study of the authors concerning the classical linear heat equation. We present variants of the result having different methods of proofs and also consider finite polynomial decay rates instead of unlimited m.

In this article, a notion of Schauder equivalence relation ℝℕ/L is introduced, where L is a linear subspace of ℝℕ and the unit vectors form a Schauder basis of L. The main theorem is to show that the following conditions are equivalent:

(1) the unit vector basis is boundedly complete;

(2) L is a Fσ in ℝℕ;

(3) ℝℕ/L is Borel reducible to ℓ∞.

We show that any Schauder equivalence relation generalized by a basis of ℓ2 is Borel bireducible to ℝℕ/ℓ2 itself, but it is not true for bases of c0 or ℓ1. Furthermore, among all Schauder equivalence relations generated by sequences in c0, we find the minimum and the maximum elements with respect to Borel reducibility.

Through appropriate choices of elements in the underlying iterated function system, the methodology of fractal interpolation enables us to associate a family of continuous self-referential functions with a prescribed real-valued continuous function on a real compact interval. This procedure elicits what is referred to as an α-fractal operator on , the space of all real-valued continuous functions defined on a compact interval I. With an eye towards connecting fractal functions with other branches of mathematics, in this paper we continue to investigate the fractal operator in more general spaces such as the space of all bounded functions and the Lebesgue space , and in some standard spaces of smooth functions such as the space of k-times continuously differentiable functions, Hölder spaces and Sobolev spaces . Using properties of the α-fractal operator, the existence of Schauder bases consisting of self-referential functions for these function spaces is established.

This article explores the properties of fractal interpolation functions with variable scaling parameters, in the context of smooth fractal functions. The first part extends the Barnsley–Harrington theorem for differentiability of fractal functions and the fractal analogue of Hermite interpolation to the present setting. The general result is applied on a special class of iterated function systems in order to develop differentiability of the so-called $\boldsymbol{{\it\alpha}}$-fractal functions. This leads to a bounded linear map on the space ${\mathcal{C}}^{k}(I)$ which is exploited to prove the existence of a Schauder basis for ${\mathcal{C}}^{k}(I)$ consisting of smooth fractal functions.

The non-archimedean power series spaces, 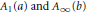${{A}_{1}}(a)\,\text{and}\,{{A}_{\infty }}(b)$, are the best known and most important examples of non-archimedean nuclear Fréchet spaces. We prove that the range of every continuous linear map from 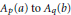${{A}_{p}}(a)\,\text{to}\,{{A}_{q}}(b)$ has a Schauder basis if either 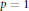$p\,=\,1$ or 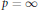$p\,=\,\infty $ and the set 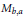${{M}_{b,a}}$ of all bounded limit points of the double sequence (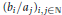${{({{b}_{i}}/{{a}_{j}})}_{i,j\in \mathbb{N}}}$ is bounded. It follows that every complemented subspace of a power series space 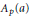${{A}_{p}}(a)$ has a Schauder basis if either 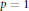$p\,=\,1$ or 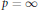$p\,=\,\infty $ and the set 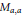${{M}_{a,a}}$ is bounded.

The Möbius inversion formula for a locally finite partially ordered set is realized as a Lagrange inversion formula. Schauder bases are introduced to interpret Möbius inversion.