We give sufficient conditions for the non-triviality of the Poisson boundary of random walks on 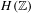 $H(\mathbb{Z})$ and its subgroups. The group
$H(\mathbb{Z})$ and its subgroups. The group 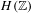 $H(\mathbb{Z})$ is the group of piecewise projective homeomorphisms over the integers defined by Monod [Groups of piecewise projective homeomorphisms. Proc. Natl Acad. Sci. USA110(12) (2013), 4524–4527]. For a finitely generated subgroup
$H(\mathbb{Z})$ is the group of piecewise projective homeomorphisms over the integers defined by Monod [Groups of piecewise projective homeomorphisms. Proc. Natl Acad. Sci. USA110(12) (2013), 4524–4527]. For a finitely generated subgroup 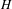 $H$ of
$H$ of  $H(\mathbb{Z})$, we prove that either
$H(\mathbb{Z})$, we prove that either 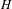 $H$ is solvable or every measure on
$H$ is solvable or every measure on 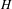 $H$ with finite first moment that generates it as a semigroup has non-trivial Poisson boundary. In particular, we prove the non-triviality of the Poisson boundary of measures on Thompson’s group
$H$ with finite first moment that generates it as a semigroup has non-trivial Poisson boundary. In particular, we prove the non-triviality of the Poisson boundary of measures on Thompson’s group  $F$ that generate it as a semigroup and have finite first moment, which answers a question by Kaimanovich [Thompson’s group
$F$ that generate it as a semigroup and have finite first moment, which answers a question by Kaimanovich [Thompson’s group  $F$ is not Liouville. Groups, Graphs and Random Walks (London Mathematical Society Lecture Note Series). Eds. T. Ceccherini-Silberstein, M. Salvatori and E. Sava-Huss. Cambridge University Press, Cambridge, 2017, pp. 300–342, 7.A].
$F$ is not Liouville. Groups, Graphs and Random Walks (London Mathematical Society Lecture Note Series). Eds. T. Ceccherini-Silberstein, M. Salvatori and E. Sava-Huss. Cambridge University Press, Cambridge, 2017, pp. 300–342, 7.A].
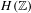 $H(\mathbb{Z})$ of Monod
$H(\mathbb{Z})$ of Monod