Given a set 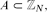 $A\subset\mathbb{Z}_{N}$, we say that a function
$A\subset\mathbb{Z}_{N}$, we say that a function 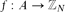 $f\colon A \to \mathbb{Z}_{N}$ is a Freiman homomorphism if f(a)+f(b)=f(c)+f(d) whenever a,b,c,d ∈ A satisfy a+b=c+d. This notion was introduced by Freiman in the 1970s, and plays an important role in the field of additive combinatorics. We say that A is linear if the only Freiman homomorphisms are functions of the form f(x) = ax+b.
$f\colon A \to \mathbb{Z}_{N}$ is a Freiman homomorphism if f(a)+f(b)=f(c)+f(d) whenever a,b,c,d ∈ A satisfy a+b=c+d. This notion was introduced by Freiman in the 1970s, and plays an important role in the field of additive combinatorics. We say that A is linear if the only Freiman homomorphisms are functions of the form f(x) = ax+b.
Suppose the elements of A are chosen independently at random, each with probability p. We shall look at the following question: For which values of p=p(N) is A linear with high probability as N → ∞? We show that if p=(2logN − ω(N))1/3N−2/3, where ω(N) → ∞ as N → ∞, then A is not linear with high probability, whereas if p=N−1/2+ε for any ε>0 then A is linear with high probability.
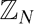 $\mathbb{Z}_{N}$
$\mathbb{Z}_{N}$