Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T23:26:21.381Z Has data issue: false hasContentIssue false
  • English
  • Français

Freiman Homomorphisms of Random Subsets of 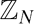$\mathbb{Z}_{N}$

Published online by Cambridge University Press:  11 June 2013

GONZALO FIZ PONTIVEROS
GONZALO FIZ PONTIVEROS*
Affiliation:
IMPA, Estrada Dona Castorina 110, Jardim Botânico, Rio de Janeiro, RJ, Brazil (e-mail: gf232@cam.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a set 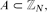$A\subset\mathbb{Z}_{N}$, we say that a function 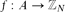$f\colon A \to \mathbb{Z}_{N}$ is a Freiman homomorphism if f(a)+f(b)=f(c)+f(d) whenever a,b,c,d ∈ A satisfy a+b=c+d. This notion was introduced by Freiman in the 1970s, and plays an important role in the field of additive combinatorics. We say that A is linear if the only Freiman homomorphisms are functions of the form f(x) = ax+b.

Suppose the elements of A are chosen independently at random, each with probability p. We shall look at the following question: For which values of p=p(N) is A linear with high probability as N → ∞? We show that if p=(2logN − ω(N))1/3N−2/3, where ω(N) → ∞ as N → ∞, then A is not linear with high probability, whereas if p=N−1/2+ε for any ε>0 then A is linear with high probability.

Keywords

Primary 05D40Secondary 11B75
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 4 , July 2013 , pp. 592 - 611
Copyright
Copyright © Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alon, N. and Spencer, J. (2008) The Probabilistic Method, Wiley Series in Discrete Mathematics and Optimization, Wiley-Interscience.Google Scholar
[2]Babai, L., Simonovits, M. and Spencer, J. (1990) Extremal subgraphs of random graphs. J. Graph Theory 14 599–622.Google Scholar
[3]Balogh, J., Morris, R. and Samotij, W. (2012) Independent sets in hypergraphs. arXiv:1204.6530v1.Google Scholar
[4]Conlon, D. and Gowers, W. T. (2010) Combinatorial theorems in sparse random sets. arXiv:1011.4310v1.Google Scholar
[5]Freiman, G. (1973) Foundations of a Structural Theory of Set Addition, Vol. 3 of Translations of Mathematical Monographs, AMS.Google Scholar
[6]Kim, J. H. and Vu, V. (2000) Concentration of multivariate polynomials and its applications. Combinatorica 20 417–434.Google Scholar
[7]Kohayakawa, Y., Rödl, V. and Łuczak, T. (1996) Arithmetic progressions of length three in subsets of a random set. Acta Arithmetica 75, 133–163.CrossRefGoogle Scholar
[8]Ruzsa, I. (1994) Generalized arithmetical progressions and sumsets. Acta Math. Hungar. 65 379–388.Google Scholar
[9]Saxton, D. and Thomason, A. (2012) Hypergraph containers. arXiv:1204.6595v1.Google Scholar
[10]Schacht, M. (2009) Extremal results for random discrete structures. Submitted.Google Scholar
[11]Szemerédi, E. (1975) On sets of integers containing no k elements in arithmetic progression. Acta Arithmetica 27 199–245.Google Scholar
[12]Tao, T. and Vu, V. (2006) Additive Combinatorics, Cambridge University Press.Google Scholar
[13]Turán, P. (1941) Eine Extremalaufgabe aus der Graphentheorie. Mat. Fiz. Lapok 48 436–452.Google Scholar
[14]Vu, V. (2002) Concentration of non-Lipschitz functions and applications. Random Struct. Alg. 20 262–316.Google Scholar