1 results
On a Localisation Sequence for the K-Theory of Skew Power Series Rings
-
- Journal:
- Journal of K-Theory / Volume 11 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 21 February 2013, pp. 125-154
- Print publication:
- February 2013
-
- Article
- Export citation
-
Let B = A[[t;σ,δ]] be a skew power series ring such that σ is given by an inner automorphism of B. We show that a certain Waldhausen localisation sequence involving the K-theory of B splits into short split exact sequences. In the case that A is noetherian we show that this sequence is given by the localisation sequence for a left denominator set S in B. If B = ℤp[[G]] happens to be the Iwasawa algebra of a p-adic Lie group G ≅ H ⋊ ℤp, this set S is Venjakob's canonical Ore set. In particular, our result implies that
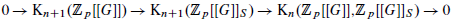
is split exact for each n ≥ 0. We also prove the corresponding result for the localisation of ℤp[[G]][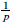
] with respect to the Ore set S*. Both sequences play a major role in non-commutative Iwasawa theory.
] with respect to the Ore set 