Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-29T04:11:27.765Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Localisation Sequence for the K-Theory of Skew Power Series Rings

Published online by Cambridge University Press:  21 February 2013

Malte Witte
Malte Witte*
Affiliation:
Ruprecht-Karls-Universität Heidelberg, Mathematisches Institut, Im Neuenheimer Feld 288, D-69120 Heidelberg, Germanywitte@mathi.uni-heidelberg.de
Get access

Abstract

Let B = A[[t;σ,δ]] be a skew power series ring such that σ is given by an inner automorphism of B. We show that a certain Waldhausen localisation sequence involving the K-theory of B splits into short split exact sequences. In the case that A is noetherian we show that this sequence is given by the localisation sequence for a left denominator set S in B. If B = ℤp[[G]] happens to be the Iwasawa algebra of a p-adic Lie group G ≅ H ⋊ ℤp, this set S is Venjakob's canonical Ore set. In particular, our result implies that

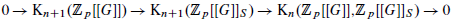
is split exact for each n ≥ 0. We also prove the corresponding result for the localisation of ℤp[[G]][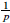] with respect to the Ore set S*. Both sequences play a major role in non-commutative Iwasawa theory.

Keywords

Skew power series ringshigher K-theoryIwasawa algebras16W6016E2011R23
Type
Research Article
Information
Journal of K-Theory , Volume 11 , Issue 1 , February 2013 , pp. 125 - 154
Copyright
Copyright © ISOPP 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bourbaki, N., Commutative Algebra 2nd edn., Elements of Mathematics, Springer, Berlin, 1989.Google Scholar
2.Bredon, G. E., Topology and Geometry, Graduate Texts in Mathematics 139, Springer, New York, 1993Google Scholar
3.Brumer, A., Pseudocompact algebras, profinite groups, and class formations, Journal of Algebra 4 (1966) 442–470Google Scholar
4.Burns, D., Algebraic p-adic L-functions in non-commutative Iwasawa theory, Publ. RIMS Kyoto 45 (2009) 75–88Google Scholar
5.Burns, D., On main conjectures in non-commutative Iwasawa theory and related conjectures (2010), preprintGoogle Scholar
6.Burns, D. & Venjakob, O., On descent theory and main conjectures in non-commuative Iwasawa theory, J. Inst. Math. Jussieu 5 (2011) 59–118Google Scholar
7.Coates, J., Fukaya, T., Kato, K., Sujatha, R. & Venjakob, O., The GL 2 main conjecture for elliptic curves without complex multiplication, Publ. Math. Inst. Hautes Etudes Sci. 101 (2005) 163–208Google Scholar
8.Fukaya, T. & Kato, K., A formulation of conjectures on p-adic zeta functions in non-commutative Iwasawa theory, In: Proceedings of the St. Petersburg Mathematical Society, Amer. Math. Soc. Transl. Ser. 2, XII, 1–85, American Math. Soc., Providence, RI, 2006Google Scholar
9.Gabriel, P., Des catégories abéliennes, Bull. Soc. Math. France 90 (1962) 323–448Google Scholar
10.Goodearl, K. R. & Warfield, R. B., An introduction to noncommutative noetherian rings, London Math. Soc. Student Texts 61, Cambridge Univ. Press, Cambridge, 2004Google Scholar
11.Kakde, M., The main conjecture of Iwasawa theory for totally real fields (2011), preprintGoogle Scholar
12.Lam, T. Y., A first course in noncommutative rings, Graduate Texts in Mathematics 131, Springer, Berlin, 1991Google Scholar
13.Muro, F. & Tonks, A., The 1-type of a Waldhausen K-theory spectrum, Advances in Mathematics 216(1) (2007) 178–211CrossRefGoogle Scholar
14.Neukirch, J., Schmidt, A. & Wingberg, K., Cohomology of Number Fields, Grundlehren der mathematischen Wissenschaften 323, Springer Verlag, Berlin Heidelberg, 2000Google Scholar
15.Ritter, J. & Weiss, A., Toward equivariant Iwasawa theory, Manuscripta Math. 109(2) (2002) 131–146CrossRefGoogle Scholar
16.Rüschoff, C., Topologische und vollständige Schiefmonoidringe lokal proendlicher, eigentlicher Monoide, Diplomarbeit, Ruprecht-Karls-Universität Heidelberg (2011),Google Scholar
17.Schneider, P., p-adic Lie groups, Grundlehren der Mathematischen Wissenschaften 344, Springer, Heidelberg, 2011Google Scholar
18.Schneider, P. & Venjakob, O., On the codimension of modules over skew power series rings with applications to Iwasawa algebras, J. Pure and Applied Algebra 204 (2006) 349–367Google Scholar
19.Schneider, P. & Venjakob, O., Localisations and completions of skew power series rings, Am. J. Math. 132(1) (2010) 1–36Google Scholar
20.Serre, J.-P., Linear representations of finite groups, Graduate Texts in Mathematics 42, Springer-Verlag, New York, 1977Google Scholar
21.Thomason, R. W. & Trobaugh, T., Higher algebraic K-theory of schemes and derived categories, In: The Grothendieck Festschrift, Progr. Math., III, 247–435, Birkhäuser, 1990CrossRefGoogle Scholar
22.Venjakob, O., Characteristic elements in noncommutative Iwasawa theory, J. reine angew. Math. 583 (2005) 193–236Google Scholar
23.Waldhausen, F., Algebraic K-theory of spaces, In: Algebraic and Geometric Topology, Lecture Notes in Mathematics 1126, Springer, Berlin Heidelberg, 1985 318–419CrossRefGoogle Scholar
24.Warner, S., Topological Rings, North-Holland Mathematical Studies 178, Elsevier, Amsterdam, 1993Google Scholar
25.Washington, L. C., Introduction to Cyclotomic Fields, Graduate Texts in Mathematics 83, Springer-Verlag, New York, 1997CrossRefGoogle Scholar
26.Weibel, C. & Yao, D., Localization for the K-theory of noncommutative rings, In: Algebraic K-Theory, Commutative Algebra, and Algebraic Geometry, Contemporary Mathematics 126, AMS, 1992 219–230Google Scholar
27.Witte, M., Noncommutative Iwasawa main conjectures for varieties over finite fields, Ph.D. thesis, Universität Leipzig (2008), http://d-nb.info/995008124/34Google Scholar
28.Witte, M., Noncommutative L-functions for varieties over finite fields (2009), preprintGoogle Scholar
29Witte, M., On a noncommutative Iwasawa main conjecture for varieties over finite fields (2010), preprint, to appear in JEMSGoogle Scholar