Let $\pi$ be a discrete group, and let $G$ be a compact-connected Lie group. Then, there is a map $\Theta \colon \mathrm {Hom}(\pi,G)_0\to \mathrm {map}_*(B\pi,BG)_0$ between the null components of the spaces of homomorphisms and based maps, which sends a homomorphism to the induced map between classifying spaces. Atiyah and Bott studied this map for $\pi$ a surface group, and showed that it is surjective in rational cohomology. In this paper, we prove that the map $\Theta$ is surjective in rational cohomology for $\pi =\mathbb {Z}^m$ and the classical group $G$ except for $SO(2n)$, and that it is not surjective for $\pi =\mathbb {Z}^m$ with $m\ge 3$ and $G=SO(2n)$ with $n\ge 4$. As an application, we consider the surjectivity of the map $\Theta$ in rational cohomology for $\pi$ a finitely generated nilpotent group. We also consider the dimension of the cokernel of the map $\Theta$ in rational homotopy groups for $\pi =\mathbb {Z}^m$ and the classical groups $G$ except for $SO(2n)$.

Let G be a compact connected Lie group, and let 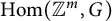$\operatorname {Hom}({\mathbb {Z}}^m,G)$ be the space of pairwise commuting m-tuples in G. We study the problem of which primes $p \operatorname {Hom}({\mathbb {Z}}^m,G)_1$, the connected component of 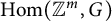$\operatorname {Hom}({\mathbb {Z}}^m,G)$ containing the element $(1,\ldots ,1)$, has p-torsion in homology. We will prove that 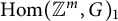$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$ for 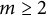$m\ge 2$ has p-torsion in homology if and only if p divides the order of the Weyl group of G for 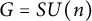$G=SU(n)$ and some exceptional groups. We will also compute the top homology of 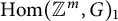$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$ and show that $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$ always has 2-torsion in homology whenever G is simply-connected and simple. Our computation is based on a new homotopy decomposition of 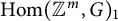$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$, which is of independent interest and enables us to connect torsion in homology to the combinatorics of the Weyl group.