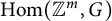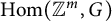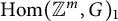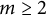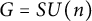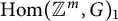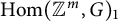1 Introduction
Let
![]() $\pi $
be a discrete group, and let G be a compact connected Lie group. Let
$\pi $
be a discrete group, and let G be a compact connected Lie group. Let
![]() $\operatorname {Hom}(\pi ,G)$
denote the space of homomorphisms from
$\operatorname {Hom}(\pi ,G)$
denote the space of homomorphisms from
![]() $\pi $
to G, having the induced topology of the space of continuous maps from
$\pi $
to G, having the induced topology of the space of continuous maps from
![]() $\pi $
to G. In this paper, we study torsion in the homology of
$\pi $
to G. In this paper, we study torsion in the homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
, the connected component of
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
, the connected component of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)$
containing the trivial homomorphism.
$\operatorname {Hom}({\mathbb {Z}}^m,G)$
containing the trivial homomorphism.
The space
![]() $\operatorname {Hom}(\pi ,G)$
has connections to diverse contexts of mathematics and physics [Reference Borel, Friedman and Morgan10, Reference Goldman15, Reference Kac and Smilga20, Reference Wehrheim27–Reference Witten29], and the topology of
$\operatorname {Hom}(\pi ,G)$
has connections to diverse contexts of mathematics and physics [Reference Borel, Friedman and Morgan10, Reference Goldman15, Reference Kac and Smilga20, Reference Wehrheim27–Reference Witten29], and the topology of
![]() $\operatorname {Hom}(\pi ,G)$
has been intensely studied in recent years, especially when
$\operatorname {Hom}(\pi ,G)$
has been intensely studied in recent years, especially when
![]() $\pi $
is a free abelian group. The space
$\pi $
is a free abelian group. The space
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)$
is identified with the space of commuting m-tuples in G, so that it is often called the space of commuting elements (see [Reference Adem and Cohen1–Reference Adem, Gómez and Gritschacher3, Reference Baird, Jeffrey and Selick5, Reference Baird6, Reference Bergeron and Silberman8, Reference Crabb13, Reference Gómez, Pettet and Souto16, Reference Kishimoto and Takeda21, Reference Ramras and Stafa24–Reference Takeda26] and the references therein for the topology of
$\operatorname {Hom}({\mathbb {Z}}^m,G)$
is identified with the space of commuting m-tuples in G, so that it is often called the space of commuting elements (see [Reference Adem and Cohen1–Reference Adem, Gómez and Gritschacher3, Reference Baird, Jeffrey and Selick5, Reference Baird6, Reference Bergeron and Silberman8, Reference Crabb13, Reference Gómez, Pettet and Souto16, Reference Kishimoto and Takeda21, Reference Ramras and Stafa24–Reference Takeda26] and the references therein for the topology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)$
). In particular, Baird [Reference Baird6] described the cohomology of
$\operatorname {Hom}({\mathbb {Z}}^m,G)$
). In particular, Baird [Reference Baird6] described the cohomology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
over a field of characteristic not dividing the order of the Weyl group of G or zero as a certain ring of invariants of the Weyl group. Based on this result, Ramras and Stafa [Reference Ramras and Stafa24] gave a formula for the Poincaré series of
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
over a field of characteristic not dividing the order of the Weyl group of G or zero as a certain ring of invariants of the Weyl group. Based on this result, Ramras and Stafa [Reference Ramras and Stafa24] gave a formula for the Poincaré series of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
. We start with recalling this formula. Let W denote the Weyl group of G, and let
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
. We start with recalling this formula. Let W denote the Weyl group of G, and let
![]() $\mathbb {F}$
be a field of characteristic not dividing the order of W or zero. Then Ramras and Stafa [Reference Ramras and Stafa24] proved that the Poincaré series of the cohomology of
$\mathbb {F}$
be a field of characteristic not dividing the order of W or zero. Then Ramras and Stafa [Reference Ramras and Stafa24] proved that the Poincaré series of the cohomology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
over
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
over
![]() $\mathbb {F}$
is given by
$\mathbb {F}$
is given by
 $$ \begin{align*} \frac{\prod_{i=1}^r(1-t^{2d_i})}{|W|}\sum_{w\in W}\frac{\det(1+tw)^m}{\det(1-t^2w)}, \end{align*} $$
$$ \begin{align*} \frac{\prod_{i=1}^r(1-t^{2d_i})}{|W|}\sum_{w\in W}\frac{\det(1+tw)^m}{\det(1-t^2w)}, \end{align*} $$
where
![]() $d_1,\ldots ,d_r$
are the characteristic degrees of W, that is, the rational cohomology of G is an exterior algebra generated by elements of degrees
$d_1,\ldots ,d_r$
are the characteristic degrees of W, that is, the rational cohomology of G is an exterior algebra generated by elements of degrees
![]() $2d_1-1,\ldots ,2d_r-1$
. A more explicit formula for the Poincaré series was obtained by the authors [Reference Kishimoto and Takeda21], and a minimal generating set of the cohomology over
$2d_1-1,\ldots ,2d_r-1$
. A more explicit formula for the Poincaré series was obtained by the authors [Reference Kishimoto and Takeda21], and a minimal generating set of the cohomology over
![]() $\mathbb {F}$
was also obtained there. An explicit description of the cohomology of
$\mathbb {F}$
was also obtained there. An explicit description of the cohomology of
![]() $\operatorname {Hom}({\mathbb {Z}}^2,G)_1$
over
$\operatorname {Hom}({\mathbb {Z}}^2,G)_1$
over
![]() $\mathbb {F}$
for G of rank two was obtained by the second author [Reference Takeda26]. Notice that the Poincaré series is independent of the ground field
$\mathbb {F}$
for G of rank two was obtained by the second author [Reference Takeda26]. Notice that the Poincaré series is independent of the ground field
![]() $\mathbb {F}$
as long as its characteristic does not divide the order of W or is zero. Then we immediately get the nonexistence of torsion in homology.
$\mathbb {F}$
as long as its characteristic does not divide the order of W or is zero. Then we immediately get the nonexistence of torsion in homology.
Lemma 1.1 The homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
has p-torsion in homology only when p divides the order of W.
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
has p-torsion in homology only when p divides the order of W.
On the other hand, as for the existence of torsion in the homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
, there are only a few results, the proofs of which do not extend to more general cases. Adem and Cohen [Reference Adem and Cohen1] proved a stable splitting of
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
, there are only a few results, the proofs of which do not extend to more general cases. Adem and Cohen [Reference Adem and Cohen1] proved a stable splitting of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)$
, and Baird, Jeffrey, and Selick [Reference Baird, Jeffrey and Selick5] and Crabb [Reference Crabb13] described the splitting summands for
$\operatorname {Hom}({\mathbb {Z}}^m,G)$
, and Baird, Jeffrey, and Selick [Reference Baird, Jeffrey and Selick5] and Crabb [Reference Crabb13] described the splitting summands for
![]() $G=SU(2)$
explicitly. As a result, we can conclude that
$G=SU(2)$
explicitly. As a result, we can conclude that
![]() $\operatorname {Hom}({\mathbb {Z}}^m,SU(2))_1$
has 2-torsion in homology for
$\operatorname {Hom}({\mathbb {Z}}^m,SU(2))_1$
has 2-torsion in homology for
![]() $m\ge 2$
. Recently, Adem, Gómez, and Gritschacher [Reference Adem, Gómez and Gritschacher3] computed the second homology group of
$m\ge 2$
. Recently, Adem, Gómez, and Gritschacher [Reference Adem, Gómez and Gritschacher3] computed the second homology group of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
, and so by combining with the result on the fundamental group by Gómez, Pettet, and Souto [Reference Gómez, Pettet and Souto16],
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
, and so by combining with the result on the fundamental group by Gómez, Pettet, and Souto [Reference Gómez, Pettet and Souto16],
![]() $\operatorname {Hom}({\mathbb {Z}}^m,Sp(n))_1$
has 2-torsion in homology for
$\operatorname {Hom}({\mathbb {Z}}^m,Sp(n))_1$
has 2-torsion in homology for
![]() $m\ge 3$
. These are all known torsion in homology so far.
$m\ge 3$
. These are all known torsion in homology so far.
1.1 Results
By Lemma 1.1, we must know the order of the Weyl group of a Lie group. Then we give a table of the order of the Weyl groups of compact simply-connected simple Lie groups.
Now, we state our results.
Theorem 1.2 The homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,SU(n))_1$
for
$\operatorname {Hom}({\mathbb {Z}}^m,SU(n))_1$
for
![]() $m\ge 2$
has p-torsion if and only if
$m\ge 2$
has p-torsion if and only if
![]() $p\le n$
.
$p\le n$
.
Since the Weyl group of
![]() $SU(n)$
is of order
$SU(n)$
is of order
![]() $n!$
, it follows from Lemma 1.1 that
$n!$
, it follows from Lemma 1.1 that
![]() $\operatorname {Hom}({\mathbb {Z}}^m,SU(n))_1$
has p-torsion in homology for all possible primes p. We will also prove a similar result for some exceptional groups.
$\operatorname {Hom}({\mathbb {Z}}^m,SU(n))_1$
has p-torsion in homology for all possible primes p. We will also prove a similar result for some exceptional groups.
Theorem 1.3 Let
![]() $G=G_2,F_4,E_6$
. Then
$G=G_2,F_4,E_6$
. Then
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
for
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
for
![]() $m\ge 2$
has p-torsion in homology if and only if p divides the order of the Weyl group of G.
$m\ge 2$
has p-torsion in homology if and only if p divides the order of the Weyl group of G.
Then for
![]() $G=G_2,F_4,E_6$
,
$G=G_2,F_4,E_6$
,
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
with
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
with
![]() $m\ge 2$
has all possible torsion in homology. So the homology of
$m\ge 2$
has all possible torsion in homology. So the homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
with
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
with
![]() $m\ge 2$
for
$m\ge 2$
for
![]() $G=SU(n),G_2,F_4,E_6$
are quite complicated. We will also show the existence of some torsion in the homology of
$G=SU(n),G_2,F_4,E_6$
are quite complicated. We will also show the existence of some torsion in the homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
for other Lie groups G, though incomplete (see Section 7 and Corollary 1.5 for details). Our next result is on the top homology of
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
for other Lie groups G, though incomplete (see Section 7 and Corollary 1.5 for details). Our next result is on the top homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
(see [Reference Kishimoto and Takeda21] for the top rational homology).
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
(see [Reference Kishimoto and Takeda21] for the top rational homology).
Theorem 1.4 Let G be a compact simply-connected simple Lie group of rank n, and let
 $$\begin{align*}t= \begin{cases} \dim G+n(m-1)-1,&m\text{ is even,}\\ \dim G+n(m-1),&m\text{ is odd}. \end{cases} \end{align*}$$
$$\begin{align*}t= \begin{cases} \dim G+n(m-1)-1,&m\text{ is even,}\\ \dim G+n(m-1),&m\text{ is odd}. \end{cases} \end{align*}$$
Then the top homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
is given by
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
is given by
 $$\begin{align*}H_t(\operatorname{Hom}({\mathbb{Z}}^m,G)_1)\cong \begin{cases} {\mathbb{Z}}/2,&m\text{ is even,}\\ {\mathbb{Z}},&m\text{ is odd}. \end{cases} \end{align*}$$
$$\begin{align*}H_t(\operatorname{Hom}({\mathbb{Z}}^m,G)_1)\cong \begin{cases} {\mathbb{Z}}/2,&m\text{ is even,}\\ {\mathbb{Z}},&m\text{ is odd}. \end{cases} \end{align*}$$
Since
![]() $\operatorname {Hom}({\mathbb {Z}}^2,G)_1$
is a retract of
$\operatorname {Hom}({\mathbb {Z}}^2,G)_1$
is a retract of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
for
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
for
![]() $m\ge 2$
, we immediately obtain the following corollary.
$m\ge 2$
, we immediately obtain the following corollary.
Corollary 1.5 Let G be a compact simply-connected simple Lie group. Then
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
for
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
for
![]() $m\ge 2$
has 2-torsion in homology.
$m\ge 2$
has 2-torsion in homology.
Let
![]() $\pi $
be a finitely generated nilpotent group whose abelianization is of rank m. We can extend our results to
$\pi $
be a finitely generated nilpotent group whose abelianization is of rank m. We can extend our results to
![]() $\operatorname {Hom}(\pi ,G)_1$
as follows. Let
$\operatorname {Hom}(\pi ,G)_1$
as follows. Let
![]() $G({\mathbb {C}})$
be a complexification of G. Then Bergeron [Reference Bergeron7] proved that
$G({\mathbb {C}})$
be a complexification of G. Then Bergeron [Reference Bergeron7] proved that
![]() $\operatorname {Hom}(\pi ,G)$
is a deformation retract of
$\operatorname {Hom}(\pi ,G)$
is a deformation retract of
![]() $\operatorname {Hom}(\pi ,G({\mathbb {C}}))$
. Moreover, Bergeron and Silberman [Reference Bergeron and Silberman8] proved that there is a homotopy equivalence
$\operatorname {Hom}(\pi ,G({\mathbb {C}}))$
. Moreover, Bergeron and Silberman [Reference Bergeron and Silberman8] proved that there is a homotopy equivalence
![]() $\operatorname {Hom}(\pi ,G({\mathbb {C}}))_1\simeq \operatorname {Hom}({\mathbb {Z}}^m,G({\mathbb {C}}))_1$
. Then we get a homotopy equivalence
$\operatorname {Hom}(\pi ,G({\mathbb {C}}))_1\simeq \operatorname {Hom}({\mathbb {Z}}^m,G({\mathbb {C}}))_1$
. Then we get a homotopy equivalence
and so all the results above also hold for
![]() $\operatorname {Hom}(\pi ,G)_1$
.
$\operatorname {Hom}(\pi ,G)_1$
.
1.2 Summary of computation
We compute the homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
in three steps: the first step is to give a new homotopy decomposition of
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
in three steps: the first step is to give a new homotopy decomposition of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
, namely, we will describe
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
, namely, we will describe
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
as a homotopy colimit, the second step is to extract the top line of (a variant of) the Bousfield–Kan spectral sequence for the homotopy colimit in the first step, and the third step is to encode the information of the top line extracted in the second step into the combinatorial data of the extended Dynkin diagram of G.
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
as a homotopy colimit, the second step is to extract the top line of (a variant of) the Bousfield–Kan spectral sequence for the homotopy colimit in the first step, and the third step is to encode the information of the top line extracted in the second step into the combinatorial data of the extended Dynkin diagram of G.
Let G act on
![]() $\operatorname {Hom}(\pi ,G)$
by conjugation. Then the quotient space, denoted by
$\operatorname {Hom}(\pi ,G)$
by conjugation. Then the quotient space, denoted by
![]() $\operatorname {Rep}(\pi ,G)$
, is called the representation space or the character variety, which has been studied in a variety of contexts [Reference Atiyah and Bott4, Reference Culler and Shalen14, Reference Hitchin18]. We will show that if G is simply-connected and simple, then
$\operatorname {Rep}(\pi ,G)$
, is called the representation space or the character variety, which has been studied in a variety of contexts [Reference Atiyah and Bott4, Reference Culler and Shalen14, Reference Hitchin18]. We will show that if G is simply-connected and simple, then
![]() $\operatorname {Rep}({\mathbb {Z}},G)$
, the quotient of
$\operatorname {Rep}({\mathbb {Z}},G)$
, the quotient of
![]() $\operatorname {Hom}({\mathbb {Z}},G)_1=G$
, is naturally identified with the closure of a Weyl alcove which is an n-simplex whose facets are defined by simple roots and the highest root, where G is of rank n. We consider the composite
$\operatorname {Hom}({\mathbb {Z}},G)_1=G$
, is naturally identified with the closure of a Weyl alcove which is an n-simplex whose facets are defined by simple roots and the highest root, where G is of rank n. We consider the composite
where the first map is the mth projection and the second map is the quotient map. We will see that the fiber of
![]() $\pi $
is constant as long as the point belongs to the interior of some face of
$\pi $
is constant as long as the point belongs to the interior of some face of
![]() $\Delta ^n$
. Let
$\Delta ^n$
. Let
![]() $\sigma _0$
denote the barycenter of a face
$\sigma _0$
denote the barycenter of a face
![]() $\sigma $
of
$\sigma $
of
![]() $\Delta ^n$
, and let
$\Delta ^n$
, and let
![]() $P(\Delta ^n)$
denote the face poset of
$P(\Delta ^n)$
denote the face poset of
![]() $\Delta ^n$
. Then we get a functor
$\Delta ^n$
. Then we get a functor
and a new homotopy decomposition in the first step is the following.
Theorem 1.6 (Theorem 3.2)
Let G be a compact simply-connected simple Lie group. Then there is a homeomorphism
This homotopy decomposition seems to be of independent interest. We will see that if m even, then for each
![]() $\sigma \in P(\Delta ^n)$
,
$\sigma \in P(\Delta ^n)$
,
![]() $F_m(\sigma )$
is of dimension
$F_m(\sigma )$
is of dimension
![]() $\dim G+n(m-2)$
and its top homology is isomorphic with
$\dim G+n(m-2)$
and its top homology is isomorphic with
![]() ${\mathbb {Z}}$
. Thus, we can consider the pinch map onto the top cell of
${\mathbb {Z}}$
. Thus, we can consider the pinch map onto the top cell of
![]() $F_m(\sigma )$
. This enables us to extract (a variant of) the Bousfield–Kan spectral sequence for
$F_m(\sigma )$
. This enables us to extract (a variant of) the Bousfield–Kan spectral sequence for
![]() $\operatorname {hocolim} F_m$
, which is the second step. The pinch map onto the top cell can be explicitly described in terms faces of
$\operatorname {hocolim} F_m$
, which is the second step. The pinch map onto the top cell can be explicitly described in terms faces of
![]() $\Delta ^n$
. Then, since faces of
$\Delta ^n$
. Then, since faces of
![]() $\Delta ^n$
are defined by simple roots and the highest weight, the computation of the extracted top line can be connected to the extended Dynkin diagram, which is the third step.
$\Delta ^n$
are defined by simple roots and the highest weight, the computation of the extracted top line can be connected to the extended Dynkin diagram, which is the third step.
2 Triangulation of a maximal torus
Hereafter, let G denote a compact simply-connected simple Lie group such that
![]() ${\operatorname {rank}} G=n$
and
${\operatorname {rank}} G=n$
and
![]() $\dim G=d$
. Let T and W denote a maximal torus and the Weyl group of G, respectively. This section constructs a W-equivariant triangulation of a maximal torus T, which will play the fundamental role in our study. Let
$\dim G=d$
. Let T and W denote a maximal torus and the Weyl group of G, respectively. This section constructs a W-equivariant triangulation of a maximal torus T, which will play the fundamental role in our study. Let
![]() ${\mathfrak {t}}$
be the Lie algebra of T, and let
${\mathfrak {t}}$
be the Lie algebra of T, and let
![]() $\Phi $
be the set of roots of G. Recall that the Stiefel diagram is defined by
$\Phi $
be the set of roots of G. Recall that the Stiefel diagram is defined by
 $$\begin{align*}\bigcup_{\substack{\alpha\in\Phi\\i\in{\mathbb{Z}}}}\alpha^{-1}(i), \end{align*}$$
$$\begin{align*}\bigcup_{\substack{\alpha\in\Phi\\i\in{\mathbb{Z}}}}\alpha^{-1}(i), \end{align*}$$
which is a union of hyperplanes in
![]() ${\mathfrak {t}}$
, where each
${\mathfrak {t}}$
, where each
![]() $\alpha ^{-1}(i)$
is called a wall in the Stiefel diagram. For example, the Stiefel diagram of
$\alpha ^{-1}(i)$
is called a wall in the Stiefel diagram. For example, the Stiefel diagram of
![]() $Sp(2)$
is given as follows, where integer points are indicated by white points.
$Sp(2)$
is given as follows, where integer points are indicated by white points.

Since G is simple, its Stiefel diagram is a simplicial complex such that every k-face is included in an intersection of exactly
![]() $n-k$
walls.
$n-k$
walls.
Lemma 2.1 If two vertices v and
![]() $v+w$
of the Stiefel diagram of G are joined by an edge, then w is a vertex of the Stiefel diagram which is joined with the vertex
$v+w$
of the Stiefel diagram of G are joined by an edge, then w is a vertex of the Stiefel diagram which is joined with the vertex
![]() $0$
by an edge.
$0$
by an edge.
Proof Since v and
![]() $v+w$
are joined by an edge,
$v+w$
are joined by an edge,
for some roots
![]() $\theta _1,\ldots ,\theta _n$
and integers
$\theta _1,\ldots ,\theta _n$
and integers
![]() $k_1,\ldots ,k_n$
, where
$k_1,\ldots ,k_n$
, where
![]() $\epsilon =\pm 1$
. Then
$\epsilon =\pm 1$
. Then
which is a vertex of the Stiefel diagram. Moreover, since
![]() $\epsilon =\pm 1$
,
$\epsilon =\pm 1$
,
![]() $0$
and w are joined by an edge on the line
$0$
and w are joined by an edge on the line
![]() $\theta _1^{-1}(0)\cap \cdots \cap \theta _{n-1}^{-1}(0)$
, completing the proof.
$\theta _1^{-1}(0)\cap \cdots \cap \theta _{n-1}^{-1}(0)$
, completing the proof.
Each connected component of the complement of the Stiefel diagram is called a Weyl alcove. Since G is simple and of rank n, the closure of each Weyl alcove is an n-simplex. Let
![]() $\alpha _1,\ldots ,\alpha _n$
be simple roots, and let
$\alpha _1,\ldots ,\alpha _n$
be simple roots, and let
![]() $\widetilde {\alpha }$
be the highest root of G. We shall consider the following closure of a Weyl alcove:
$\widetilde {\alpha }$
be the highest root of G. We shall consider the following closure of a Weyl alcove:
Let L denote the group generated by coroot shifts. Since G is simply-connected, L is identified with the integer lattice of
![]() ${\mathfrak {t}}$
. The affine Weyl group of G is defined by
${\mathfrak {t}}$
. The affine Weyl group of G is defined by
Then
![]() $W_{\mathrm {aff}}$
acts on
$W_{\mathrm {aff}}$
acts on
![]() ${\mathfrak {t}}$
. Since this action fixes the Stiefel diagram,
${\mathfrak {t}}$
. Since this action fixes the Stiefel diagram,
![]() $W_{\mathrm {aff}}$
permutes Weyl alcoves. By [Reference Humphreys19, Theorem 4.5, Part I], we have the following.
$W_{\mathrm {aff}}$
permutes Weyl alcoves. By [Reference Humphreys19, Theorem 4.5, Part I], we have the following.
Lemma 2.2 The affine Weyl group
![]() $W_{\mathrm {aff}}$
permutes Weyl alcoves of G simply transitively.
$W_{\mathrm {aff}}$
permutes Weyl alcoves of G simply transitively.
Let
![]() $\mathcal {P}$
be the union of all closures of Weyl alcoves around the origin. Then
$\mathcal {P}$
be the union of all closures of Weyl alcoves around the origin. Then
![]() $\mathcal {P}$
is a simplicial convex n-polytope.
$\mathcal {P}$
is a simplicial convex n-polytope.
Lemma 2.3 If
![]() $\sigma $
is a face of
$\sigma $
is a face of
![]() $\mathcal {P}$
such that
$\mathcal {P}$
such that
![]() $\sigma +a$
is also a face of
$\sigma +a$
is also a face of
![]() $\mathcal {P}$
for some
$\mathcal {P}$
for some
![]() $0\ne a\in L$
, then both
$0\ne a\in L$
, then both
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma +a$
must be faces of the boundary of
$\sigma +a$
must be faces of the boundary of
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
Proof Since W permutes Weyl chambers simply transitively, it follows from Lemma 2.2 that
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma +a$
must not include the vertex
$\sigma +a$
must not include the vertex
![]() $0\in \mathcal {P}$
, completing the proof.
$0\in \mathcal {P}$
, completing the proof.
By Lemma 2.3, we can define
where
![]() $\sigma \sim \sigma +a$
if
$\sigma \sim \sigma +a$
if
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma +a$
are faces of the boundary of P for some
$\sigma +a$
are faces of the boundary of P for some
![]() $a\in L$
. Clearly, the inclusion
$a\in L$
. Clearly, the inclusion
![]() $\mathcal {P}\to {\mathfrak {t}}$
induces a homeomorphism
$\mathcal {P}\to {\mathfrak {t}}$
induces a homeomorphism
Since G is simply-connected, L is the integer lattice of
![]() ${\mathfrak {t}}$
, so a torus
${\mathfrak {t}}$
, so a torus
![]() ${\mathfrak {t}}/L$
coincides with a maximal torus T. Then we get the following.
${\mathfrak {t}}/L$
coincides with a maximal torus T. Then we get the following.
Proposition 2.4 The homeomorphism (2.1) is a W-equivariant triangulation of T.
Proof The homeomorphism (2.1) is obviously W-equivariant, so it remains to prove
![]() $\mathcal {Q}$
is a simplicial complex. It suffices to show that there is no vertex v of the boundary of
$\mathcal {Q}$
is a simplicial complex. It suffices to show that there is no vertex v of the boundary of
![]() $\mathcal {P}$
such that v and
$\mathcal {P}$
such that v and
![]() $v+a$
are joined by an edge of
$v+a$
are joined by an edge of
![]() $\mathcal {P}$
for
$\mathcal {P}$
for
![]() $0\ne a\in L$
. This has been already proved in Lemma 2.1.
$0\ne a\in L$
. This has been already proved in Lemma 2.1.
Proposition 2.5 The quotient space
![]() $T/W$
is naturally identified with
$T/W$
is naturally identified with
![]() $\Delta $
.
$\Delta $
.
Proof This follows from [Reference Humphreys19, Theorem 4.8, Part I].
A maximal torus T will always be equipped with a W-equivariant triangulation (2.1). We consider objects related to the triangulation of T. Let
![]() $\sigma $
be a face of T. Then there is a face
$\sigma $
be a face of T. Then there is a face
![]() $\widetilde {\sigma }$
of
$\widetilde {\sigma }$
of
![]() $\mathcal {Q}$
which is mapped onto
$\mathcal {Q}$
which is mapped onto
![]() $\sigma $
. We can associate with
$\sigma $
. We can associate with
![]() $\widetilde {\sigma }$
roots corresponding to walls including
$\widetilde {\sigma }$
roots corresponding to walls including
![]() $\widetilde {\sigma }$
. Lifts of
$\widetilde {\sigma }$
. Lifts of
![]() $\sigma $
are related by translations in L, so that the associated roots are equal. Then we can associate roots to
$\sigma $
are related by translations in L, so that the associated roots are equal. Then we can associate roots to
![]() $\sigma $
. Let
$\sigma $
. Let
![]() $\Phi (\sigma )$
denote the set of roots associated with
$\Phi (\sigma )$
denote the set of roots associated with
![]() $\sigma $
. Clearly, we have the following.
$\sigma $
. Clearly, we have the following.
Lemma 2.6 If faces
![]() $\sigma ,\tau $
of T satisfy
$\sigma ,\tau $
of T satisfy
![]() $\sigma <\tau $
, then
$\sigma <\tau $
, then
Let
![]() $\sigma $
be a face of T. We define two groups associated with
$\sigma $
be a face of T. We define two groups associated with
![]() $\sigma $
. Let
$\sigma $
. Let
![]() $W(\sigma )$
be a subgroup of W generated by reflections corresponding to roots in
$W(\sigma )$
be a subgroup of W generated by reflections corresponding to roots in
![]() $\Phi (\sigma )$
, and let
$\Phi (\sigma )$
, and let
We have
![]() $W(\sigma )=1$
and
$W(\sigma )=1$
and
![]() $Z(\sigma )=T$
for
$Z(\sigma )=T$
for
![]() $\dim \sigma =n$
. Notice that since we may assume
$\dim \sigma =n$
. Notice that since we may assume
![]() $\Delta $
is a face of T, we can consider the groups
$\Delta $
is a face of T, we can consider the groups
![]() $W(\sigma )$
and
$W(\sigma )$
and
![]() $Z(\sigma )$
for a face
$Z(\sigma )$
for a face
![]() $\sigma $
of
$\sigma $
of
![]() $\Delta $
.
$\Delta $
.
Lemma 2.7 If faces
![]() $\sigma ,\tau $
of T satisfy
$\sigma ,\tau $
of T satisfy
![]() $\sigma <\tau $
, then
$\sigma <\tau $
, then
Proof The first statement follows from Lemma 2.6. Since
![]() $Z(\sigma )$
is the union of all maximal tori including
$Z(\sigma )$
is the union of all maximal tori including
![]() $\sigma $
, the second statement is true.
$\sigma $
, the second statement is true.
3 Homotopy decomposition
This section proves a new homotopy decomposition of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
(Theorem 1.6). Let
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
(Theorem 1.6). Let
![]() $\pi $
be a discrete group, and let
$\pi $
be a discrete group, and let
![]() $\operatorname {Rep}(\pi ,G)$
be the quotient of the conjugation action of G on
$\operatorname {Rep}(\pi ,G)$
be the quotient of the conjugation action of G on
![]() $\operatorname {Hom}(\pi ,G)$
as in Section 1. Then we have
$\operatorname {Hom}(\pi ,G)$
as in Section 1. Then we have
which is identified with
![]() $\Delta $
by Proposition 2.5. We will consider the composite
$\Delta $
by Proposition 2.5. We will consider the composite
where the first map is the mth projection and the second map is the quotient map. We aim to identify the fibers of the map
![]() $\pi $
. We consider a map
$\pi $
. We consider a map
It is proved in [Reference Borel9] that the map
![]() $\phi $
is surjective. Let the Weyl group W act on
$\phi $
is surjective. Let the Weyl group W act on
![]() $G/T\times T^m$
by
$G/T\times T^m$
by
for
![]() $(gT,t_1,\ldots ,t_m)\in G/T\times T^m$
and
$(gT,t_1,\ldots ,t_m)\in G/T\times T^m$
and
![]() $w\in W$
. Then the map
$w\in W$
. Then the map
![]() $\phi $
is invariant under the action of W, and so it induces a surjective map
$\phi $
is invariant under the action of W, and so it induces a surjective map
Lemma 3.1 If
![]() $x,y\in \Delta $
belong to the interior of a common face, then
$x,y\in \Delta $
belong to the interior of a common face, then
Proof Suppose that
![]() $x,y\in \Delta $
belong to the interior of a common face
$x,y\in \Delta $
belong to the interior of a common face
![]() $\sigma $
, and consider the adjoint action of G on
$\sigma $
, and consider the adjoint action of G on
![]() $G^{m-1}\times {\mathfrak {t}}$
. Then for each
$G^{m-1}\times {\mathfrak {t}}$
. Then for each
![]() $w\in W$
and
$w\in W$
and
![]() $(t_1,\ldots ,t_{m-1})\in T^{m-1}$
, the isotropy subgroups of
$(t_1,\ldots ,t_{m-1})\in T^{m-1}$
, the isotropy subgroups of
![]() $(t_1,\ldots ,t_{m-1},wx)$
and
$(t_1,\ldots ,t_{m-1},wx)$
and
![]() $(t_1,\ldots ,t_{m-1},wy)$
are equal. Thus, since
$(t_1,\ldots ,t_{m-1},wy)$
are equal. Thus, since
where
![]() $W\cdot x\cong W\cdot y\cong W/W(\sigma )$
, we obtain
$W\cdot x\cong W\cdot y\cong W/W(\sigma )$
, we obtain
![]() $\pi ^{-1}(x)\cong \pi ^{-1}(y)$
, as stated.
$\pi ^{-1}(x)\cong \pi ^{-1}(y)$
, as stated.
Let
![]() $P(\Delta )$
denote the face poset of
$P(\Delta )$
denote the face poset of
![]() $\Delta $
, and let
$\Delta $
, and let
![]() $\sigma _0$
denote the barycenter of a face
$\sigma _0$
denote the barycenter of a face
![]() $\sigma \in P(\Delta )$
. For
$\sigma \in P(\Delta )$
. For
![]() $\sigma \in P(\Delta )$
, let
$\sigma \in P(\Delta )$
, let
![]() $\phi _\sigma \colon G/T\times T^{m-1}\to \pi ^{-1}(\sigma _0)$
denote the restriction of the quotient map (3.1). Observe that for
$\phi _\sigma \colon G/T\times T^{m-1}\to \pi ^{-1}(\sigma _0)$
denote the restriction of the quotient map (3.1). Observe that for
![]() $\sigma <\tau \in P(\Delta )$
, there is a natural map
$\sigma <\tau \in P(\Delta )$
, there is a natural map
![]() $q_{\sigma ,\tau }\colon \pi ^{-1}(\tau _0)\to \pi ^{-1}(\sigma _0)$
satisfying a commutative diagram
$q_{\sigma ,\tau }\colon \pi ^{-1}(\tau _0)\to \pi ^{-1}(\sigma _0)$
satisfying a commutative diagram

Clearly, we have
for
![]() $\sigma <\tau <\nu \in P(\Delta )$
. Let
$\sigma <\tau <\nu \in P(\Delta )$
. Let
![]() $\iota _{\tau ,\sigma }\colon \sigma \to \tau $
denote the inclusion for
$\iota _{\tau ,\sigma }\colon \sigma \to \tau $
denote the inclusion for
![]() $\sigma <\tau \in P(\Delta )$
. Then the above observation implies that
$\sigma <\tau \in P(\Delta )$
. Then the above observation implies that
 $$ \begin{align} \operatorname{Hom}({\mathbb{Z}}^m,G)_1=\left(\coprod_{\sigma\in P(\Delta)}\pi^{-1}(\sigma_0)\times\sigma\right)/\sim, \end{align} $$
$$ \begin{align} \operatorname{Hom}({\mathbb{Z}}^m,G)_1=\left(\coprod_{\sigma\in P(\Delta)}\pi^{-1}(\sigma_0)\times\sigma\right)/\sim, \end{align} $$
where
![]() $(x,\iota _{\tau ,\sigma }(y))\sim (q_{\sigma ,\tau }(x),y)$
for
$(x,\iota _{\tau ,\sigma }(y))\sim (q_{\sigma ,\tau }(x),y)$
for
![]() $(x,y)\in \pi ^{-1}(\tau _0)\times \sigma \subset \pi ^{-1}(\tau _0)\times \tau $
. Define a functor
$(x,y)\in \pi ^{-1}(\tau _0)\times \sigma \subset \pi ^{-1}(\tau _0)\times \tau $
. Define a functor
such that
![]() $F_m(\tau>\sigma )=q_{\sigma ,\tau }$
, where we understand a poset P as a category by assuming an inequality
$F_m(\tau>\sigma )=q_{\sigma ,\tau }$
, where we understand a poset P as a category by assuming an inequality
![]() $x>y\in P$
as a unique morphism
$x>y\in P$
as a unique morphism
![]() $x\to y$
. Thus, by (3.2), we obtain the following.
$x\to y$
. Thus, by (3.2), we obtain the following.
Theorem 3.2 There is a homeomorphism
We further look into
![]() $F_m(\sigma )$
for
$F_m(\sigma )$
for
![]() $\sigma \in P(\Delta )$
. Let
$\sigma \in P(\Delta )$
. Let
![]() $P(X)$
denote the face poset of a regular CW complex X, and let
$P(X)$
denote the face poset of a regular CW complex X, and let
![]() $\sigma $
be a face of
$\sigma $
be a face of
![]() $\Delta $
. For
$\Delta $
. For
![]() $\tau =\tau _1\times \cdots \times \tau _{m-1}\in P(T^{m-1})$
, let
$\tau =\tau _1\times \cdots \times \tau _{m-1}\in P(T^{m-1})$
, let
![]() $Z(\tau )=Z(\tau _1)\cap \cdots \cap Z(\tau _{m-1})$
. For
$Z(\tau )=Z(\tau _1)\cap \cdots \cap Z(\tau _{m-1})$
. For
![]() $\tau <\mu \in P(T^{m-1})$
, let
$\tau <\mu \in P(T^{m-1})$
, let
![]() $\iota _{\mu ,\tau }\colon \tau \to \mu $
denote the inclusion, and let
$\iota _{\mu ,\tau }\colon \tau \to \mu $
denote the inclusion, and let
be the natural projection. Then we have
 $$\begin{align*}\pi^{-1}(\sigma_0)=\left(\left(\coprod_{\tau\in P(T^{m-1})}G/Z(\tau)\cap Z(\sigma)\times\tau\right)/\sim\right)/W(\sigma), \end{align*}$$
$$\begin{align*}\pi^{-1}(\sigma_0)=\left(\left(\coprod_{\tau\in P(T^{m-1})}G/Z(\tau)\cap Z(\sigma)\times\tau\right)/\sim\right)/W(\sigma), \end{align*}$$
where
![]() $(x,\iota _{\mu ,\tau }(y))\sim (q_{\tau ,\mu }^\sigma (x),y)$
for
$(x,\iota _{\mu ,\tau }(y))\sim (q_{\tau ,\mu }^\sigma (x),y)$
for
![]() $(x,y)\in G/Z(\mu )\cap Z(\sigma )\times \tau \subset G/Z(\mu )\cap Z(\sigma )\times \mu $
and the quotient by
$(x,y)\in G/Z(\mu )\cap Z(\sigma )\times \tau \subset G/Z(\mu )\cap Z(\sigma )\times \mu $
and the quotient by
![]() $W(\sigma )$
is taken by the action of W on
$W(\sigma )$
is taken by the action of W on
![]() $G/T\times T^{m-1}$
. Now, we define a functor
$G/T\times T^{m-1}$
. Now, we define a functor
where
![]() $F_m^\sigma (\mu>\tau )$
is the projection
$F_m^\sigma (\mu>\tau )$
is the projection
![]() $q^\sigma _{\tau ,\mu }$
. Then we obtain the following.
$q^\sigma _{\tau ,\mu }$
. Then we obtain the following.
Proposition 3.3 For
![]() $\sigma \in P(\Delta )$
, there is a natural homeomorphism
$\sigma \in P(\Delta )$
, there is a natural homeomorphism
Hereafter, we let
Since the maximal dimension of
![]() $F_m^\sigma (\tau )\times \tau $
for
$F_m^\sigma (\tau )\times \tau $
for
![]() $\tau \in P(T^{m-1})$
is
$\tau \in P(T^{m-1})$
is
![]() $q_m$
, we get the following.
$q_m$
, we get the following.
Corollary 3.4 For each
![]() $\sigma \in P(\Delta )$
,
$\sigma \in P(\Delta )$
,
![]() $\dim F_m(\sigma )=q_m$
.
$\dim F_m(\sigma )=q_m$
.
Example 3.5 We examine Theorem 3.2 in the
![]() $G=SU(2)$
case. Since
$G=SU(2)$
case. Since
![]() ${\operatorname {rank}} SU(2)=1$
,
${\operatorname {rank}} SU(2)=1$
,
![]() $\Delta $
is a 1-simplex. Let
$\Delta $
is a 1-simplex. Let
![]() $v_0,v_1$
be vertices of
$v_0,v_1$
be vertices of
![]() $\Delta $
, and let e be an edge of
$\Delta $
, and let e be an edge of
![]() $\Delta $
. Since
$\Delta $
. Since
![]() $G=SU(2)$
,
$G=SU(2)$
,
![]() $\{v_0,v_1\}$
corresponds to the center, so we have
$\{v_0,v_1\}$
corresponds to the center, so we have
for
![]() $i=0,1$
. By Proposition 3.3, we also have
$i=0,1$
. By Proposition 3.3, we also have
Then Theorem 3.2 for
![]() $G=SU(2)$
is equivalent to that there is a homotopy pushout
$G=SU(2)$
is equivalent to that there is a homotopy pushout

For
![]() $m=2$
, the map
$m=2$
, the map
![]() $g_2\colon S^2\times S^1\to S^3$
is of degree 2. On the other hand, the map
$g_2\colon S^2\times S^1\to S^3$
is of degree 2. On the other hand, the map
![]() $\operatorname {Hom}({\mathbb {Z}}^{m-1},SU(2))_1\to \operatorname {Hom}({\mathbb {Z}}^m,SU(2))_1$
has a retraction. Then the homotopy pushout above for
$\operatorname {Hom}({\mathbb {Z}}^{m-1},SU(2))_1\to \operatorname {Hom}({\mathbb {Z}}^m,SU(2))_1$
has a retraction. Then the homotopy pushout above for
![]() $m=2$
splits after a suspension, and so we get a stable homotopy equivalence
$m=2$
splits after a suspension, and so we get a stable homotopy equivalence
which was previously proved by Baird, Jeffrey, and Selick [Reference Baird, Jeffrey and Selick5] and Crabb [Reference Crabb13] in different ways.
4 The functor
 $\widehat {F}_m$
$\widehat {F}_m$
This section defines a functor
![]() $\widehat {F}_m\colon P(\Delta )\to \mathbf {Top}$
which extracts the top line of (a variant of) the Bousfield–Kan spectral sequence for
$\widehat {F}_m\colon P(\Delta )\to \mathbf {Top}$
which extracts the top line of (a variant of) the Bousfield–Kan spectral sequence for
![]() $\operatorname {hocolim} F_m$
. First, we compute some homology of
$\operatorname {hocolim} F_m$
. First, we compute some homology of
![]() $F_m(\sigma )$
. To this end, we recall the work of Baird [Reference Baird6] on the cohomology of
$F_m(\sigma )$
. To this end, we recall the work of Baird [Reference Baird6] on the cohomology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
over a field whose characteristic does not divide the order of W. Let K be a topological group acting on a space X, and let
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
over a field whose characteristic does not divide the order of W. Let K be a topological group acting on a space X, and let
![]() $f\colon X\to Y$
be a K-equivariant map, where K acts trivially on Y. Let
$f\colon X\to Y$
be a K-equivariant map, where K acts trivially on Y. Let
![]() $\bar {f}\colon X/K\to Y$
be the induced map from f. Baird [Reference Baird6] defined that a map
$\bar {f}\colon X/K\to Y$
be the induced map from f. Baird [Reference Baird6] defined that a map
![]() $f\colon X\to Y$
is an
$f\colon X\to Y$
is an
![]() $\mathbb {F}$
-cohomological principal K-bundle if f is a closed surjection and
$\mathbb {F}$
-cohomological principal K-bundle if f is a closed surjection and
for each
![]() $y\in Y$
, where
$y\in Y$
, where
![]() $\mathbb {F}$
is a field. The main result of Baird’s work [Reference Baird6] is the following.
$\mathbb {F}$
is a field. The main result of Baird’s work [Reference Baird6] is the following.
Theorem 4.1 Let K be a finite group, and let
![]() $\mathbb {F}$
be a field of characteristic prime to
$\mathbb {F}$
be a field of characteristic prime to
![]() $|K|$
. If a map
$|K|$
. If a map
![]() $f\colon X\to Y$
is an
$f\colon X\to Y$
is an
![]() $\mathbb {F}$
-cohomological principal K-bundle, where X is paracompact and Hausdorff, then there is an isomorphism
$\mathbb {F}$
-cohomological principal K-bundle, where X is paracompact and Hausdorff, then there is an isomorphism
This theorem is applicable to
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
as in [Reference Baird6].
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
as in [Reference Baird6].
Theorem 4.2 Let
![]() $\mathbb {F}$
be a field of characteristic prime to
$\mathbb {F}$
be a field of characteristic prime to
![]() $|W|$
. Then the map (3.1) is an
$|W|$
. Then the map (3.1) is an
![]() $\mathbb {F}$
-cohomological principal W-bundle, so that there is an isomorphism
$\mathbb {F}$
-cohomological principal W-bundle, so that there is an isomorphism
We also apply Theorem 4.1 to
![]() $F_m(\sigma )$
. The following lemma is immediate from the definition of a cohomological principal bundle.
$F_m(\sigma )$
. The following lemma is immediate from the definition of a cohomological principal bundle.
Lemma 4.3 If
![]() $f\colon X\to Y$
is an
$f\colon X\to Y$
is an
![]() $\mathbb {F}$
-cohomological principal K-bundle, then for any closed subset
$\mathbb {F}$
-cohomological principal K-bundle, then for any closed subset
![]() $Z\subset Y$
, the natural map
$Z\subset Y$
, the natural map
is an
![]() $\mathbb {F}$
-cohomological principal K-bundle.
$\mathbb {F}$
-cohomological principal K-bundle.
We consider special representations of W.
Lemma 4.4
-
(1) The W-representation
 $H^n(T;{\mathbb {Q}})$
is the sign representation.
$H^n(T;{\mathbb {Q}})$
is the sign representation. -
(2) For
 $n\ge 2$
, the W-representation
$n\ge 2$
, the W-representation
 $H^{n-1}(T;{\mathbb {Q}})$
does not include the trivial representation.
$H^{n-1}(T;{\mathbb {Q}})$
does not include the trivial representation. -
(3) The W-representation
 $H^{\dim G-n}(G/T;{\mathbb {Q}})$
is the sign representation.
$H^{\dim G-n}(G/T;{\mathbb {Q}})$
is the sign representation.
Proof (1) Since each reflection of W changes the orientation of
![]() ${\mathfrak {t}}$
and
${\mathfrak {t}}$
and
![]() $H^1(T;{\mathbb {R}})\cong {\mathfrak {t}}$
as a W-module,
$H^1(T;{\mathbb {R}})\cong {\mathfrak {t}}$
as a W-module,
![]() $H^n(T;{\mathbb {Q}})\cong \Lambda ^nH^1(T;{\mathbb {Q}})$
is the sign representation of W.
$H^n(T;{\mathbb {Q}})\cong \Lambda ^nH^1(T;{\mathbb {Q}})$
is the sign representation of W.
(2) By [Reference Bredon12, Theorem III.2.4], there is an isomorphism
Then, by Proposition 2.5,
![]() $H^{n-1}(T;{\mathbb {Q}})^W=0$
for
$H^{n-1}(T;{\mathbb {Q}})^W=0$
for
![]() $n\ge 2$
, completing the proof.
$n\ge 2$
, completing the proof.
(3) By Theorem 4.1, there is an isomorphism
because
![]() $\operatorname {Hom}({\mathbb {Z}},G)_1=G$
. Then we get
$\operatorname {Hom}({\mathbb {Z}},G)_1=G$
. Then we get
So since
![]() $H^{d-n}(G/T;{\mathbb {Q}})\cong H^n(T;{\mathbb {Q}})\cong {\mathbb {Q}}$
,
$H^{d-n}(G/T;{\mathbb {Q}})\cong H^n(T;{\mathbb {Q}})\cong {\mathbb {Q}}$
,
![]() $H^{d-n}(G/T;{\mathbb {Q}})\otimes H^n(T;{\mathbb {Q}})$
is the trivial W-representation. Thus, the statement follows from (1).
$H^{d-n}(G/T;{\mathbb {Q}})\otimes H^n(T;{\mathbb {Q}})$
is the trivial W-representation. Thus, the statement follows from (1).
Now, we compute the homology of
![]() $F_m(\sigma )$
.
$F_m(\sigma )$
.
Lemma 4.5 For
![]() $\sigma \in P(\Delta )$
, we have
$\sigma \in P(\Delta )$
, we have
 $$\begin{align*}H_{q_m}(F_m(\sigma))\cong \begin{cases} {\mathbb{Z,}}&m\text{ is even or }\dim\sigma=n,\\ 0,&m\text{ is odd and }\dim\sigma<n. \end{cases} \end{align*}$$
$$\begin{align*}H_{q_m}(F_m(\sigma))\cong \begin{cases} {\mathbb{Z,}}&m\text{ is even or }\dim\sigma=n,\\ 0,&m\text{ is odd and }\dim\sigma<n. \end{cases} \end{align*}$$
Proof By Corollary 3.4,
![]() $H_{q_m}(F_m(\sigma ))$
is a free abelian group. Then we compute
$H_{q_m}(F_m(\sigma ))$
is a free abelian group. Then we compute
![]() $\dim H^{q_m}(F_m(\sigma );{\mathbb {Q}})$
because
$\dim H^{q_m}(F_m(\sigma );{\mathbb {Q}})$
because
![]() ${\operatorname {rank}} H_{q_m}(F_m(\sigma ))=\dim H^{q_m}(F_m(\sigma );{\mathbb {Q}})$
. By Theorem 4.2 and Lemma 4.3, the map
${\operatorname {rank}} H_{q_m}(F_m(\sigma ))=\dim H^{q_m}(F_m(\sigma );{\mathbb {Q}})$
. By Theorem 4.2 and Lemma 4.3, the map
is a
![]() ${\mathbb {Q}}$
-cohomological principal W-bundle. The space
${\mathbb {Q}}$
-cohomological principal W-bundle. The space
![]() $\phi ^{-1}(\pi ^{-1}(\sigma _0))=G/T\times T^{m-1}\times W/W(\sigma )$
has
$\phi ^{-1}(\pi ^{-1}(\sigma _0))=G/T\times T^{m-1}\times W/W(\sigma )$
has
![]() $|W|/|W(\sigma )|$
connected components and permutes these components transitively such that each component is fixed by the action of
$|W|/|W(\sigma )|$
connected components and permutes these components transitively such that each component is fixed by the action of
![]() $W(\sigma )$
. Then the map
$W(\sigma )$
. Then the map
is a
![]() ${\mathbb {Q}}$
-cohomological principal
${\mathbb {Q}}$
-cohomological principal
![]() $W(\sigma )$
-bundle. Thus, by Theorem 4.1, we obtain an isomorphism
$W(\sigma )$
-bundle. Thus, by Theorem 4.1, we obtain an isomorphism
If
![]() $\dim \sigma =n$
, then
$\dim \sigma =n$
, then
![]() $W(\sigma )=1$
, implying
$W(\sigma )=1$
, implying
![]() $\dim H^{q_m}(F_m(\sigma );{\mathbb {Q}})=1$
. Now, we assume
$\dim H^{q_m}(F_m(\sigma );{\mathbb {Q}})=1$
. Now, we assume
![]() $\dim \sigma <n$
, or equivalently,
$\dim \sigma <n$
, or equivalently,
![]() $W(\sigma )\ne 1$
. By Lemma 4.4,
$W(\sigma )\ne 1$
. By Lemma 4.4,
![]() $H^{d-n}(G/T;{\mathbb {Q}})$
and
$H^{d-n}(G/T;{\mathbb {Q}})$
and
![]() $H^n(T;{\mathbb {Q}})$
are the sign representation of W. Then it follows from the Künneth theorem that
$H^n(T;{\mathbb {Q}})$
are the sign representation of W. Then it follows from the Künneth theorem that
![]() $H^{q_m}(G/T\times T^{m-1};{\mathbb {Q}})$
is the tensor product of m copies of the sign representation of W. Thus, since
$H^{q_m}(G/T\times T^{m-1};{\mathbb {Q}})$
is the tensor product of m copies of the sign representation of W. Thus, since
![]() $W(\sigma )\ne 1$
, we obtain
$W(\sigma )\ne 1$
, we obtain
 $$\begin{align*}H^{q_m}(G/T\times T^{m-1};{\mathbb{Q}})^{W(\sigma)}\cong \begin{cases} {\mathbb{Q,}}&m\text{ is even,}\\ 0,&m\text{ is odd.} \end{cases} \end{align*}$$
$$\begin{align*}H^{q_m}(G/T\times T^{m-1};{\mathbb{Q}})^{W(\sigma)}\cong \begin{cases} {\mathbb{Q,}}&m\text{ is even,}\\ 0,&m\text{ is odd.} \end{cases} \end{align*}$$
Therefore, the proof is complete.
Now, we define a functor
![]() $\widehat {F}_m\colon P(\Delta )\to \mathbf {Top}$
by
$\widehat {F}_m\colon P(\Delta )\to \mathbf {Top}$
by
 $$\begin{align*}\widehat{F}_m(\sigma)= \begin{cases} S^{q_m},&m\text{ is even or }\dim\sigma=n,\\ *,&m\text{ is odd and }\dim\sigma<n, \end{cases} \end{align*}$$
$$\begin{align*}\widehat{F}_m(\sigma)= \begin{cases} S^{q_m},&m\text{ is even or }\dim\sigma=n,\\ *,&m\text{ is odd and }\dim\sigma<n, \end{cases} \end{align*}$$
such that the map
![]() $F_m(\sigma>\tau )$
is the constant map for m odd and a map of degree
$F_m(\sigma>\tau )$
is the constant map for m odd and a map of degree
![]() $|W(\tau )|/|W(\sigma )|$
for m even. Since
$|W(\tau )|/|W(\sigma )|$
for m even. Since
for
![]() $\sigma>\tau >\mu \in P(\Delta )$
,
$\sigma>\tau >\mu \in P(\Delta )$
,
![]() $\widehat {F}_m$
is well defined.
$\widehat {F}_m$
is well defined.
Next, we define a natural transformation
![]() $\rho \colon F_m\to \widehat {F}_m$
. For m odd,
$\rho \colon F_m\to \widehat {F}_m$
. For m odd,
![]() $\rho $
is defined by the pinch map onto the top cell
$\rho $
is defined by the pinch map onto the top cell
![]() $G/T\times T^{m-1}\to S^{q_m}$
and the constant map. Suppose m is even. For
$G/T\times T^{m-1}\to S^{q_m}$
and the constant map. Suppose m is even. For
![]() $\sigma \in P(\Delta )$
, let
$\sigma \in P(\Delta )$
, let
![]() $\mathcal {Q}(\sigma )$
be the union of the boundary of
$\mathcal {Q}(\sigma )$
be the union of the boundary of
![]() $\mathcal {P}$
and the image of all walls of the Stiefel diagram including
$\mathcal {P}$
and the image of all walls of the Stiefel diagram including
![]() $\sigma $
under the projection
$\sigma $
under the projection
![]() ${\mathfrak {t}}\to \mathcal {Q}$
, where
${\mathfrak {t}}\to \mathcal {Q}$
, where
![]() $\mathcal {Q}$
is the triangulation of T in Section 2 and
$\mathcal {Q}$
is the triangulation of T in Section 2 and
![]() ${\mathfrak {t}}$
is the Lie algebra of T. Then, by (2.1),
${\mathfrak {t}}$
is the Lie algebra of T. Then, by (2.1),
Moreover, for
![]() $\sigma>\tau \in P(\Delta )$
, we have
$\sigma>\tau \in P(\Delta )$
, we have
![]() $\mathcal {Q}(\sigma )\subset \mathcal {Q}(\tau )$
, implying there is a commutative diagram
$\mathcal {Q}(\sigma )\subset \mathcal {Q}(\tau )$
, implying there is a commutative diagram

where
![]() $\nabla \colon S^n\to \bigvee _{|W(\tau )|/|W(\sigma )|}S^n$
is the pinch map. On the other hand, a face
$\nabla \colon S^n\to \bigvee _{|W(\tau )|/|W(\sigma )|}S^n$
is the pinch map. On the other hand, a face
![]() $\tau $
of
$\tau $
of
![]() $\mathcal {Q}$
satisfies
$\mathcal {Q}$
satisfies
whenever
![]() ${\operatorname {Int}}(\tau )$
is in
${\operatorname {Int}}(\tau )$
is in
![]() $\mathcal {Q}-\mathcal {Q}(\sigma )$
, where
$\mathcal {Q}-\mathcal {Q}(\sigma )$
, where
![]() $Z(\tau )\cap Z(\sigma )$
always includes T. Then, by Proposition 3.3, there is a projection
$Z(\tau )\cap Z(\sigma )$
always includes T. Then, by Proposition 3.3, there is a projection
 $$ \begin{align} F_m(\sigma)\to&((G/T\times T^{m-2})\wedge(\mathcal{Q}/\mathcal{Q}(\sigma)))/W(\sigma)\\ &=\left((G/T\times T^{m-2})\wedge\bigvee_{|W(\sigma)|}S^n\right)/W(\sigma).\notag \end{align} $$
$$ \begin{align} F_m(\sigma)\to&((G/T\times T^{m-2})\wedge(\mathcal{Q}/\mathcal{Q}(\sigma)))/W(\sigma)\\ &=\left((G/T\times T^{m-2})\wedge\bigvee_{|W(\sigma)|}S^n\right)/W(\sigma).\notag \end{align} $$
Since
![]() $W(\sigma )$
permutes spheres in
$W(\sigma )$
permutes spheres in
![]() $\bigvee _{|W(\sigma )|}S^n$
, we get
$\bigvee _{|W(\sigma )|}S^n$
, we get
 $$\begin{align*}\left((G/T\times T^{m-2})\wedge\bigvee_{|W(\sigma)|}S^n\right)/W(\sigma)=(G/T\times T^{m-2})\wedge S^n. \end{align*}$$
$$\begin{align*}\left((G/T\times T^{m-2})\wedge\bigvee_{|W(\sigma)|}S^n\right)/W(\sigma)=(G/T\times T^{m-2})\wedge S^n. \end{align*}$$
Then, by (4.1), the map (4.2) satisfies the commutative diagram

Thus, composing with the pinch map onto the top cell
![]() $(G/T\times T^{m-2})\wedge S^n\to S^{q_m}$
, we obtain a natural transformation
$(G/T\times T^{m-2})\wedge S^n\to S^{q_m}$
, we obtain a natural transformation
![]() $\rho \colon F_m\to \widehat {F}_m$
.
$\rho \colon F_m\to \widehat {F}_m$
.
We show properties of the natural transformation
![]() $\rho \colon F_m\to \widehat {F}_m$
in homology. By the construction and Lemma 4.5, we have the following.
$\rho \colon F_m\to \widehat {F}_m$
in homology. By the construction and Lemma 4.5, we have the following.
Proposition 4.6 Let
![]() $\sigma \in P(\Delta )$
. If m is even or
$\sigma \in P(\Delta )$
. If m is even or
![]() $\dim \sigma =n$
, then the map
$\dim \sigma =n$
, then the map
![]() $\rho _\sigma \colon F_m(\sigma )\to \widehat {F}_m(\sigma )$
is an isomorphism in
$\rho _\sigma \colon F_m(\sigma )\to \widehat {F}_m(\sigma )$
is an isomorphism in
![]() $H_{q_m}$
.
$H_{q_m}$
.
The following variant of the Bousfield–Kan spectral sequence for a homotopy colimit is constructed in [Reference Hasui, Kishimoto, Takeda and Tsutaya17] (see [Reference Bousfield and Kan11, XII 4.5] for the original Bousfield–Kan spectral sequence).
Proposition 4.7 Let
![]() $F\colon P(K)\to \mathbf {Top}$
be a functor for a simplicial complex K. Then there is a spectral sequence
$F\colon P(K)\to \mathbf {Top}$
be a functor for a simplicial complex K. Then there is a spectral sequence
where
![]() $P_p(K)$
denotes the set of p-simplices of K.
$P_p(K)$
denotes the set of p-simplices of K.
By Proposition 4.6, we get the following.
Lemma 4.8 Let
![]() $E^r$
and
$E^r$
and
![]() $\widehat {E}^r$
be the spectral sequences of Proposition 4.7 for
$\widehat {E}^r$
be the spectral sequences of Proposition 4.7 for
![]() $\operatorname {hocolim} F_m$
and
$\operatorname {hocolim} F_m$
and
![]() $\operatorname {hocolim}\widehat {F}_m$
, respectively. Then the natural transformation
$\operatorname {hocolim}\widehat {F}_m$
, respectively. Then the natural transformation
![]() $\rho \colon F_m\to \widehat {F}_m$
induces an isomorphism of the top lines
$\rho \colon F_m\to \widehat {F}_m$
induces an isomorphism of the top lines
Proposition 4.9
![]() $H_*(\operatorname {hocolim}\widehat {F}_m)$
is a direct summand of
$H_*(\operatorname {hocolim}\widehat {F}_m)$
is a direct summand of
![]() $H_*(\operatorname {Hom}({\mathbb {Z}}^m,G)_1)$
for
$H_*(\operatorname {Hom}({\mathbb {Z}}^m,G)_1)$
for
![]() $*\ge q_m$
.
$*\ge q_m$
.
Proof Let
![]() $(E^r,d^r)$
and
$(E^r,d^r)$
and
![]() $(\widehat {E}^r,\hat {d}^r)$
denote the spectral sequences of Proposition 4.7 for
$(\widehat {E}^r,\hat {d}^r)$
denote the spectral sequences of Proposition 4.7 for
![]() $\operatorname {hocolim} F_m$
and
$\operatorname {hocolim} F_m$
and
![]() $\operatorname {hocolim}\widehat {F}_m$
, respectively. Let r be the smallest integer
$\operatorname {hocolim}\widehat {F}_m$
, respectively. Let r be the smallest integer
![]() $\ge 2$
such that there is a nontrivial differential
$\ge 2$
such that there is a nontrivial differential
![]() $d^r_{p,q_m-r+1}\colon E^r_{p,q_m-r+1}\to E^r_{p-r,q_m}$
for some
$d^r_{p,q_m-r+1}\colon E^r_{p,q_m-r+1}\to E^r_{p-r,q_m}$
for some
![]() $p\ge 0$
. Suppose that
$p\ge 0$
. Suppose that
![]() $d^r_{p,q_m-r+1}(x)\ne 0$
for
$d^r_{p,q_m-r+1}(x)\ne 0$
for
![]() $x\in E^r_{p,q_m-r+1}$
. Then
$x\in E^r_{p,q_m-r+1}$
. Then
![]() $E^r$
and
$E^r$
and
![]() $\widehat {E}^r$
are illustrated below, where possibly nontrivial parts are shaded.
$\widehat {E}^r$
are illustrated below, where possibly nontrivial parts are shaded.


By Lemma 4.8, the natural map
![]() $\rho _*\colon E_{p,q_m}^r\to \widehat {E}_{p,q_m}^r$
is an isomorphism, implying
$\rho _*\colon E_{p,q_m}^r\to \widehat {E}_{p,q_m}^r$
is an isomorphism, implying
This is a contradiction. Thus, we obtain
![]() $E^2_{p,q_m}\cong E^\infty _{p,q_m}$
. On the other hand, we have
$E^2_{p,q_m}\cong E^\infty _{p,q_m}$
. On the other hand, we have
![]() $\widehat {E}^2_{p,q_m}\cong \widehat {E}^\infty _{p,q_m}\cong H_{*+q_m}(\operatorname {hocolim}\widehat {F}_m)$
. Then the composite
$\widehat {E}^2_{p,q_m}\cong \widehat {E}^\infty _{p,q_m}\cong H_{*+q_m}(\operatorname {hocolim}\widehat {F}_m)$
. Then the composite
is identified with
![]() $\rho _*\colon E^2_{p,q_m}\to \widehat {E}^2_{p,q_m}$
, and so it is an isomorphism. Therefore, by Theorem 3.2, the proof is finished.
$\rho _*\colon E^2_{p,q_m}\to \widehat {E}^2_{p,q_m}$
, and so it is an isomorphism. Therefore, by Theorem 3.2, the proof is finished.
Example 4.10 We examine
![]() $\operatorname {hocolim}\widehat {F}_m$
for
$\operatorname {hocolim}\widehat {F}_m$
for
![]() $G=SU(2)$
. In this case,
$G=SU(2)$
. In this case,
![]() $\Delta $
is a 1-simplex, and so as in Example 3.5, there is a homotopy pushout involving
$\Delta $
is a 1-simplex, and so as in Example 3.5, there is a homotopy pushout involving
![]() $\operatorname {hocolim}\widehat {F}_m$
which yields a homotopy equivalence
$\operatorname {hocolim}\widehat {F}_m$
which yields a homotopy equivalence
 $$\begin{align*}\operatorname{hocolim}\widehat{F}_m\simeq \begin{cases} S^{m+2},&m\text{ is odd},\\ S^{m+1}\vee(S^{m+1}\cup_2e^{m+2}),&m\text{ is even.} \end{cases} \end{align*}$$
$$\begin{align*}\operatorname{hocolim}\widehat{F}_m\simeq \begin{cases} S^{m+2},&m\text{ is odd},\\ S^{m+1}\vee(S^{m+1}\cup_2e^{m+2}),&m\text{ is even.} \end{cases} \end{align*}$$
In particular, we can see from (3.3) that
![]() $\operatorname {hocolim}\widehat {F}_m$
computes the top homology of
$\operatorname {hocolim}\widehat {F}_m$
computes the top homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,SU(2))_1$
. This will be generalized in the next section to an arbitrary compact simply-connected simple Lie group G.
$\operatorname {Hom}({\mathbb {Z}}^m,SU(2))_1$
. This will be generalized in the next section to an arbitrary compact simply-connected simple Lie group G.
5 Top homology
This section computes the top homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
and proves Theorem 1.4. The result depends on the parity of m. We start with the case m is odd.
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
and proves Theorem 1.4. The result depends on the parity of m. We start with the case m is odd.
Theorem 5.1 If m is odd, then the top homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
is
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
is
Proof We present two proofs.
First proof. By Corollary 3.4, the
![]() $E^1$
-term of the spectral sequence of Proposition 4.7 for
$E^1$
-term of the spectral sequence of Proposition 4.7 for
![]() $\operatorname {hocolim} F_m$
is given below, where a possibly nontrivial part is shaded. Then, by degree reasons, the statement is proved.
$\operatorname {hocolim} F_m$
is given below, where a possibly nontrivial part is shaded. Then, by degree reasons, the statement is proved.

Second proof.
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
is of dimension
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
is of dimension
![]() $q_m+n$
as mentioned above, implying
$q_m+n$
as mentioned above, implying
![]() $H_{q_m+n}(\operatorname {Hom}({\mathbb {Z}}^m,G)_1)$
is a free abelian group. Then it suffices to compute the dimension of the rational cohomology
$H_{q_m+n}(\operatorname {Hom}({\mathbb {Z}}^m,G)_1)$
is a free abelian group. Then it suffices to compute the dimension of the rational cohomology
![]() $H^{q_m+n}(\operatorname {Hom}({\mathbb {Z}}^m,G)_1;{\mathbb {Q}})$
. By Theorem 4.2 and the Künneth theorem,
$H^{q_m+n}(\operatorname {Hom}({\mathbb {Z}}^m,G)_1;{\mathbb {Q}})$
. By Theorem 4.2 and the Künneth theorem,
 $$\begin{align*}H^{q_m+n}(\operatorname{Hom}({\mathbb{Z}}^m,G)_1;{\mathbb{Q}})\cong (H^{\dim G-n}(G/T;{\mathbb{Q}})\otimes\underbrace{H^n(T;{\mathbb{Q}})\otimes\cdots\otimes H^n(T;{\mathbb{Q}})}_m)^W. \end{align*}$$
$$\begin{align*}H^{q_m+n}(\operatorname{Hom}({\mathbb{Z}}^m,G)_1;{\mathbb{Q}})\cong (H^{\dim G-n}(G/T;{\mathbb{Q}})\otimes\underbrace{H^n(T;{\mathbb{Q}})\otimes\cdots\otimes H^n(T;{\mathbb{Q}})}_m)^W. \end{align*}$$
By Lemma 4.4,
![]() $H^{\dim G-n}(G/T;{\mathbb {Q}})$
and
$H^{\dim G-n}(G/T;{\mathbb {Q}})$
and
![]() $H^n(T;{\mathbb {Q}})$
are the sign representation of W, and so we get
$H^n(T;{\mathbb {Q}})$
are the sign representation of W, and so we get
![]() $\dim H^{q_m+n}(\operatorname {Hom}({\mathbb {Z}}^m,G)_1;{\mathbb {Q}})=1$
, completing the proof.
$\dim H^{q_m+n}(\operatorname {Hom}({\mathbb {Z}}^m,G)_1;{\mathbb {Q}})=1$
, completing the proof.
Next, we consider the case m is even.
Lemma 5.2 If m is even and
![]() $n\ge 2$
, then
$n\ge 2$
, then
![]() $H_{q_m+n-1}(\operatorname {Hom}({\mathbb {Z}}^m,G)_1;{\mathbb {Q}})=0$
.
$H_{q_m+n-1}(\operatorname {Hom}({\mathbb {Z}}^m,G)_1;{\mathbb {Q}})=0$
.
Proof By Lemma 4.4,
![]() $H^{n-1}(T;{\mathbb {Q}})$
does not include the trivial representation of W. Then, by arguing as in the second proof of Theorem 5.1, the statement is proved.
$H^{n-1}(T;{\mathbb {Q}})$
does not include the trivial representation of W. Then, by arguing as in the second proof of Theorem 5.1, the statement is proved.
Remark 5.3 For
![]() $n=1$
,
$n=1$
,
![]() $H^{n-1}(T;{\mathbb {Q}})$
is the trivial representation of W, so that the proof of Lemma 5.2 does not work for
$H^{n-1}(T;{\mathbb {Q}})$
is the trivial representation of W, so that the proof of Lemma 5.2 does not work for
![]() $n=1$
. The top homology of
$n=1$
. The top homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,SU(2))_1$
for m even can be deduced from the results of Baird, Jeffrey, and Selick [Reference Baird, Jeffrey and Selick5] and Crabb [Reference Crabb13]; it is given by
$\operatorname {Hom}({\mathbb {Z}}^m,SU(2))_1$
for m even can be deduced from the results of Baird, Jeffrey, and Selick [Reference Baird, Jeffrey and Selick5] and Crabb [Reference Crabb13]; it is given by
![]() $H_{m+1}(\operatorname {Hom}({\mathbb {Z}}^m,G)_1)\cong {\mathbb {Z}}/2$
.
$H_{m+1}(\operatorname {Hom}({\mathbb {Z}}^m,G)_1)\cong {\mathbb {Z}}/2$
.
Theorem 5.4 If m is even and
![]() $n\ge 2$
, then the top homology of
$n\ge 2$
, then the top homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
is
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
is
Proof Let
![]() $E^r$
and
$E^r$
and
![]() $\widehat {E}^r$
denote the spectral sequences of Proposition 4.7 for
$\widehat {E}^r$
denote the spectral sequences of Proposition 4.7 for
![]() $\operatorname {hocolim} F_m$
and
$\operatorname {hocolim} F_m$
and
![]() $\operatorname {hocolim}\widehat {F}_m$
, respectively. By Proposition 3.3,
$\operatorname {hocolim}\widehat {F}_m$
, respectively. By Proposition 3.3,
![]() $E^1_{n,*}\cong H_*(G/T\times T^{m-1})$
. Then, by Corollary 3.4,
$E^1_{n,*}\cong H_*(G/T\times T^{m-1})$
. Then, by Corollary 3.4,
![]() $E^1$
is given below, where a possibly nontrivial part is shaded.
$E^1$
is given below, where a possibly nontrivial part is shaded.

Thus,
![]() $H_*(\operatorname {Hom}({\mathbb {Z}}^m,G)_1)=0$
for
$H_*(\operatorname {Hom}({\mathbb {Z}}^m,G)_1)=0$
for
![]() $*>q_m+n$
, and by Corollary 4.8 and Lemma 5.2,
$*>q_m+n$
, and by Corollary 4.8 and Lemma 5.2,
for
![]() $i=0,1$
. Let
$i=0,1$
. Let
![]() $\sigma $
be the only one n-face of
$\sigma $
be the only one n-face of
![]() $\Delta $
, and let
$\Delta $
, and let
![]() $\tau _0,\ldots ,\tau _n$
be
$\tau _0,\ldots ,\tau _n$
be
![]() $(n-1)$
-faces of
$(n-1)$
-faces of
![]() $\Delta $
. Then
$\Delta $
. Then
where u is a generator of
![]() $H_{q_m}(S^{q_m})$
. Since
$H_{q_m}(S^{q_m})$
. Since
![]() $|W(\sigma )|=1$
and
$|W(\sigma )|=1$
and
![]() $|W(\tau _i)|=2$
for each i, we have
$|W(\tau _i)|=2$
for each i, we have
 $$\begin{align*}d^1\colon \widehat{E}^1_{n,q_m}\to\widehat{E}^1_{n-1,q_m},\quad u\otimes\sigma\mapsto 2\sum_{i=0}^n(-1)^iu\otimes\tau_i, \end{align*}$$
$$\begin{align*}d^1\colon \widehat{E}^1_{n,q_m}\to\widehat{E}^1_{n-1,q_m},\quad u\otimes\sigma\mapsto 2\sum_{i=0}^n(-1)^iu\otimes\tau_i, \end{align*}$$
implying
![]() $\widehat {E}^2_{n,q_m}=0$
, which is proved by the same way as the second proof of Theorem 5.1. Since
$\widehat {E}^2_{n,q_m}=0$
, which is proved by the same way as the second proof of Theorem 5.1. Since
![]() $\widehat {E}^1_{n-1,q_m}$
is a free abelian group,
$\widehat {E}^1_{n-1,q_m}$
is a free abelian group,
![]() $\sum _{i=0}^n(-1)^iu\otimes \tau _i\in \widehat {E}^1_{n-1,q_m}$
is a nontrivial cycle. Then, by Lemma 5.2,
$\sum _{i=0}^n(-1)^iu\otimes \tau _i\in \widehat {E}^1_{n-1,q_m}$
is a nontrivial cycle. Then, by Lemma 5.2,
![]() $\widehat {E}^2_{n-1,q_m}\cong {\mathbb {Z}}/2$
, completing the proof.
$\widehat {E}^2_{n-1,q_m}\cong {\mathbb {Z}}/2$
, completing the proof.
6 The complex
 $\Delta _p(k)$
$\Delta _p(k)$
This section provides a combinatorial way to detect torsion in the homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
. Define a subcomplex of
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
. Define a subcomplex of
![]() $\Delta $
by
$\Delta $
by
Then there is a sequence of subcomplexes
where r is given by
![]() $|W|=p^rq$
with
$|W|=p^rq$
with
![]() $(p,q)=1$
.
$(p,q)=1$
.
Example 6.1 Let
![]() $G=SU(3)$
, so that
$G=SU(3)$
, so that
![]() $\Delta $
is a 2-simplex and
$\Delta $
is a 2-simplex and
![]() $|W|=6$
. Then possibly nontrivial
$|W|=6$
. Then possibly nontrivial
![]() $\Delta _p(k)$
are
$\Delta _p(k)$
are
![]() $\Delta _2(0)$
and
$\Delta _2(0)$
and
![]() $\Delta _3(0)$
. It is easy to see that
$\Delta _3(0)$
. It is easy to see that
![]() $\Delta _2(0)$
is the 1-skeleton of
$\Delta _2(0)$
is the 1-skeleton of
![]() $\Delta $
and
$\Delta $
and
![]() $\Delta _3(0)$
is the 0-skeleton of
$\Delta _3(0)$
is the 0-skeleton of
![]() $\Delta $
.
$\Delta $
.
The following lemma will play a fundamental role in connecting the mod p homology of
![]() $\Delta _p(k)$
to p-torsion in the homology of
$\Delta _p(k)$
to p-torsion in the homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^2,G)_1$
.
$\operatorname {Hom}({\mathbb {Z}}^2,G)_1$
.
Lemma 6.2 The homology
![]() $H_*(\operatorname {hocolim}\widehat {F}_2)$
is a finite abelian group for each
$H_*(\operatorname {hocolim}\widehat {F}_2)$
is a finite abelian group for each
![]() $*>q_2$
and a finitely generated abelian group of rank 1 for
$*>q_2$
and a finitely generated abelian group of rank 1 for
![]() $*=q_2$
.
$*=q_2$
.
Proof Since
![]() $\operatorname {hocolim}\widehat {F}$
is a CW complex of finite type, the statement is equivalent to that
$\operatorname {hocolim}\widehat {F}$
is a CW complex of finite type, the statement is equivalent to that
![]() $H_*(\operatorname {hocolim}\widehat {F}_2;{\mathbb {Q}})$
is trivial for each
$H_*(\operatorname {hocolim}\widehat {F}_2;{\mathbb {Q}})$
is trivial for each
![]() $*>q_2$
and isomorphic with
$*>q_2$
and isomorphic with
![]() ${\mathbb {Q}}$
for
${\mathbb {Q}}$
for
![]() $*=q_2$
. Then we compute the rational homology of
$*=q_2$
. Then we compute the rational homology of
![]() $\operatorname {hocolim}\widehat {F}_2$
. Let
$\operatorname {hocolim}\widehat {F}_2$
. Let
![]() $C_*(-;\mathbb {F})$
denote the cellular chain complex over a field
$C_*(-;\mathbb {F})$
denote the cellular chain complex over a field
![]() $\mathbb {F}$
. We assume that a sphere
$\mathbb {F}$
. We assume that a sphere
![]() $S^{q_2}$
is given a cell decomposition
$S^{q_2}$
is given a cell decomposition
![]() $S^{q_2}=e^0\cup e^{q_2}$
. Then for
$S^{q_2}=e^0\cup e^{q_2}$
. Then for
![]() $0\le *\le n$
, we can define a map
$0\le *\le n$
, we can define a map
 $$\begin{align*}\phi\colon C_*(\Delta;{\mathbb{Q}})\to C_{*+q_2}(\operatorname{hocolim}\widehat{F}_2;{\mathbb{Q}}),\quad\sigma\mapsto \frac{|W(\sigma)|}{|W|}u\times\sigma, \end{align*}$$
$$\begin{align*}\phi\colon C_*(\Delta;{\mathbb{Q}})\to C_{*+q_2}(\operatorname{hocolim}\widehat{F}_2;{\mathbb{Q}}),\quad\sigma\mapsto \frac{|W(\sigma)|}{|W|}u\times\sigma, \end{align*}$$
where
![]() $\sigma $
is a face of
$\sigma $
is a face of
![]() $\Delta $
and u is a generator of
$\Delta $
and u is a generator of
![]() $C_{q_2}(S^{q_2};{\mathbb {Q}})\cong {\mathbb {Q}}$
. Then
$C_{q_2}(S^{q_2};{\mathbb {Q}})\cong {\mathbb {Q}}$
. Then
 $$\begin{align*}\phi(\partial\sigma)=\sum_{i=0}^{\dim\sigma}(-1)^i\frac{|W(\tau_i)|}{|W|}u\times\tau_i=\frac{|W(\sigma)|}{|W|}\sum_{i=0}^{\dim\sigma}(-1)^i\frac{|W(\tau_i)|}{|W(\sigma)|}u\times\tau_i=\partial\phi(\sigma), \end{align*}$$
$$\begin{align*}\phi(\partial\sigma)=\sum_{i=0}^{\dim\sigma}(-1)^i\frac{|W(\tau_i)|}{|W|}u\times\tau_i=\frac{|W(\sigma)|}{|W|}\sum_{i=0}^{\dim\sigma}(-1)^i\frac{|W(\tau_i)|}{|W(\sigma)|}u\times\tau_i=\partial\phi(\sigma), \end{align*}$$
where
![]() $\partial \sigma =\sum _{i=0}^{\dim \sigma }(-1)^i\tau _i$
. Thus,
$\partial \sigma =\sum _{i=0}^{\dim \sigma }(-1)^i\tau _i$
. Thus,
![]() $\phi $
is a chain map. Clearly,
$\phi $
is a chain map. Clearly,
![]() $\phi $
is bijective, and so
$\phi $
is bijective, and so
![]() $H_*(\Delta ;{\mathbb {Q}})\cong H_{*+q_2}(\operatorname {hocolim}\widehat {F}_2;{\mathbb {Q}})$
. Since
$H_*(\Delta ;{\mathbb {Q}})\cong H_{*+q_2}(\operatorname {hocolim}\widehat {F}_2;{\mathbb {Q}})$
. Since
![]() $\Delta $
is contractible, the proof is done.
$\Delta $
is contractible, the proof is done.
Now, we prove the main theorem of this section.
Theorem 6.3 The mod p homology of
![]() $\Delta _p(k)$
is nontrivial for some k if and only if
$\Delta _p(k)$
is nontrivial for some k if and only if
![]() $\operatorname {hocolim}\widehat {F}_2$
has p-torsion in homology.
$\operatorname {hocolim}\widehat {F}_2$
has p-torsion in homology.
Proof We assume that a sphere
![]() $S^{q_2}$
is given a cell decomposition
$S^{q_2}$
is given a cell decomposition
![]() $S^{q_2}=e^0\cup e^{q_2}$
. Consider a map
$S^{q_2}=e^0\cup e^{q_2}$
. Consider a map
 $$\begin{align*}\phi_k\colon C_*(\Delta_p(k);{\mathbb{Z}}/p)\to C_{*+q_2}(\operatorname{hocolim}\widehat{F}_2;{\mathbb{Z}}/p),\quad\sigma\mapsto\frac{|W(\sigma)|}{p^{r-k}}u\times\sigma, \end{align*}$$
$$\begin{align*}\phi_k\colon C_*(\Delta_p(k);{\mathbb{Z}}/p)\to C_{*+q_2}(\operatorname{hocolim}\widehat{F}_2;{\mathbb{Z}}/p),\quad\sigma\mapsto\frac{|W(\sigma)|}{p^{r-k}}u\times\sigma, \end{align*}$$
where
![]() $\sigma $
is a face of
$\sigma $
is a face of
![]() $\Delta _p(k)$
, u is a generator of
$\Delta _p(k)$
, u is a generator of
![]() $C_{q_2}(S^{q_2};{\mathbb {Z}}/p)\cong {\mathbb {Z}}/p$
and r is given by
$C_{q_2}(S^{q_2};{\mathbb {Z}}/p)\cong {\mathbb {Z}}/p$
and r is given by
![]() $|W|=p^rq$
with
$|W|=p^rq$
with
![]() $(p,q)=1$
. Then
$(p,q)=1$
. Then
 $$\begin{align*}\phi_k(\partial\sigma)=\sum_{i=0}^{\dim\sigma}(-1)^i\frac{|W(\tau_i)|}{p^{r-k}}u\times\tau_i=\frac{|W(\sigma)|}{p^{r-k}}\sum_{i=0}^{\dim\sigma}(-1)^i\frac{|W(\tau_i)|}{|W(\sigma)|}u\times\tau_i=\partial\phi_k(\sigma), \end{align*}$$
$$\begin{align*}\phi_k(\partial\sigma)=\sum_{i=0}^{\dim\sigma}(-1)^i\frac{|W(\tau_i)|}{p^{r-k}}u\times\tau_i=\frac{|W(\sigma)|}{p^{r-k}}\sum_{i=0}^{\dim\sigma}(-1)^i\frac{|W(\tau_i)|}{|W(\sigma)|}u\times\tau_i=\partial\phi_k(\sigma), \end{align*}$$
and so
![]() $\phi _k$
is a chain map.
$\phi _k$
is a chain map.
Let
![]() $P(K)$
denote the face poset of a simplicial complex K as in Section 4. Suppose that
$P(K)$
denote the face poset of a simplicial complex K as in Section 4. Suppose that
![]() $\widetilde {H}_*(\Delta _p(k);{\mathbb {Z}}/p)\ne 0$
. Then there is a non-boundary cycle
$\widetilde {H}_*(\Delta _p(k);{\mathbb {Z}}/p)\ne 0$
. Then there is a non-boundary cycle
in the reduced cellular chain complex
![]() $\widetilde {C}_*(\Delta _p(k);{\mathbb {Z}}/p)$
. We may assume that the homology class
$\widetilde {C}_*(\Delta _p(k);{\mathbb {Z}}/p)$
. We may assume that the homology class
![]() $[\alpha ]$
does not lie in the image of the natural map
$[\alpha ]$
does not lie in the image of the natural map
because we can replace
![]() $\Delta _p(k)$
with
$\Delta _p(k)$
with
![]() $\Delta _p(l)$
for some
$\Delta _p(l)$
for some
![]() $l<k$
otherwise. Since
$l<k$
otherwise. Since
![]() $\phi _k$
annihilates
$\phi _k$
annihilates
![]() $C_*(\Delta _p(k-1);{\mathbb {Z}}/p)$
,
$C_*(\Delta _p(k-1);{\mathbb {Z}}/p)$
,
 $$\begin{align*}\phi_k(\alpha)=\sum_{\sigma\in P(\Delta_p(k))-P(\Delta_p(k-1))}\frac{|W(\sigma)|}{p^{r-k}}a_\sigma(u\times\sigma)\in C_{*+q_2}(\operatorname{hocolim}\widehat{F}_2;{\mathbb{Z}}/p), \end{align*}$$
$$\begin{align*}\phi_k(\alpha)=\sum_{\sigma\in P(\Delta_p(k))-P(\Delta_p(k-1))}\frac{|W(\sigma)|}{p^{r-k}}a_\sigma(u\times\sigma)\in C_{*+q_2}(\operatorname{hocolim}\widehat{F}_2;{\mathbb{Z}}/p), \end{align*}$$
which is a cycle because
![]() $\alpha $
is a cycle and
$\alpha $
is a cycle and
![]() $\phi _k$
is a chain map. Suppose
$\phi _k$
is a chain map. Suppose
 $$\begin{align*}\phi_k(\alpha)=\partial\left(\sum_{\tau\in P(\Delta_p(k))}b_\tau(u\times\tau)\right). \end{align*}$$
$$\begin{align*}\phi_k(\alpha)=\partial\left(\sum_{\tau\in P(\Delta_p(k))}b_\tau(u\times\tau)\right). \end{align*}$$
Then we have
 $$ \begin{align*} \phi_k(\alpha)&=\partial\left(\sum_{\tau\in P(\Delta_p(k))-P(\Delta_p(k-1))}b_\tau(u\times\tau)\right)\\ &=\partial\phi_k\left(\sum_{\tau\in P(\Delta_p(k))-P(\Delta_p(k-1))}\frac{p^{r-k}}{|W(\tau)|}b_\tau\tau\right). \end{align*} $$
$$ \begin{align*} \phi_k(\alpha)&=\partial\left(\sum_{\tau\in P(\Delta_p(k))-P(\Delta_p(k-1))}b_\tau(u\times\tau)\right)\\ &=\partial\phi_k\left(\sum_{\tau\in P(\Delta_p(k))-P(\Delta_p(k-1))}\frac{p^{r-k}}{|W(\tau)|}b_\tau\tau\right). \end{align*} $$
By definition,
![]() $\phi _k$
is injective on the subgroup of
$\phi _k$
is injective on the subgroup of
![]() $C_*(\Delta _p(k);{\mathbb {Z}}/p)$
generated by faces in
$C_*(\Delta _p(k);{\mathbb {Z}}/p)$
generated by faces in
![]() $P(\Delta _p(k))-P(\Delta _p(k-1))$
. So we obtain that
$P(\Delta _p(k))-P(\Delta _p(k-1))$
. So we obtain that
![]() $\alpha $
is homologous to a cycle in
$\alpha $
is homologous to a cycle in
![]() $\Delta _p(k-1)$
. Since
$\Delta _p(k-1)$
. Since
![]() $\alpha $
is not homologous to a non-boundary cycle in
$\alpha $
is not homologous to a non-boundary cycle in
![]() $\Delta _p(k-1)$
by assumption,
$\Delta _p(k-1)$
by assumption,
![]() $\alpha $
is homologous to a boundary in
$\alpha $
is homologous to a boundary in
![]() $\Delta _p(k)$
. Then
$\Delta _p(k)$
. Then
![]() $\alpha $
itself is a boundary, which is a contradiction. Then
$\alpha $
itself is a boundary, which is a contradiction. Then
![]() $\phi _k(\alpha )$
is a non-boundary cycle in
$\phi _k(\alpha )$
is a non-boundary cycle in
![]() $C_{*+q_2}(\operatorname {hocolim}\widehat {F}_2;{\mathbb {Z}}/p)$
. If
$C_{*+q_2}(\operatorname {hocolim}\widehat {F}_2;{\mathbb {Z}}/p)$
. If
![]() $|\alpha |=0|$
, then the proof of Lemma 6.2 implies that
$|\alpha |=0|$
, then the proof of Lemma 6.2 implies that
![]() $\phi _k(\alpha )$
is not the mod p reduction of a representative of an integral homology class of infinite order. Thus, by Lemma 6.2,
$\phi _k(\alpha )$
is not the mod p reduction of a representative of an integral homology class of infinite order. Thus, by Lemma 6.2,
![]() $H_*(\operatorname {hocolim}\widehat {F}_2)$
has p-torsion in homology.
$H_*(\operatorname {hocolim}\widehat {F}_2)$
has p-torsion in homology.
Assume
![]() $\widetilde {H}_*(\Delta _p(k);{\mathbb {Z}}/p)=0$
for each k. Then we suppose
$\widetilde {H}_*(\Delta _p(k);{\mathbb {Z}}/p)=0$
for each k. Then we suppose
![]() $\operatorname {hocolim}\widehat {F}_2$
has p-torsion in homology and derive a contradiction. The
$\operatorname {hocolim}\widehat {F}_2$
has p-torsion in homology and derive a contradiction. The
![]() $E^2$
-term of the spectral sequence of Proposition 4.7 for
$E^2$
-term of the spectral sequence of Proposition 4.7 for
![]() $\operatorname {hocolim}\widehat {F}_2$
is illustrated as follows, where possibly nontrivial parts are shaded.
$\operatorname {hocolim}\widehat {F}_2$
is illustrated as follows, where possibly nontrivial parts are shaded.

Then
![]() $H_*(\operatorname {hocolim}\widehat {F}_2)$
has p-torsion only for
$H_*(\operatorname {hocolim}\widehat {F}_2)$
has p-torsion only for
![]() $*\ge q_2$
. So there is a cycle representing a p-torsion element in the homology of
$*\ge q_2$
. So there is a cycle representing a p-torsion element in the homology of
![]() $\operatorname {hocolim}\widehat {F}_2$
. We may assume that its mod p reduction
$\operatorname {hocolim}\widehat {F}_2$
. We may assume that its mod p reduction
represents a nontrivial mod p homology class of
![]() $\operatorname {hocolim}\widehat {F}_2$
. Let
$\operatorname {hocolim}\widehat {F}_2$
. Let
By definition,
![]() $\widehat {\alpha }=\widehat {\alpha }_0+\cdots +\widehat {\alpha }_r$
. Clearly,
$\widehat {\alpha }=\widehat {\alpha }_0+\cdots +\widehat {\alpha }_r$
. Clearly,
![]() $\partial \widehat {\alpha }_k$
is a linear combination of simplices in
$\partial \widehat {\alpha }_k$
is a linear combination of simplices in
![]() $P(\Delta _p(k))$
. For
$P(\Delta _p(k))$
. For
![]() $\sigma \in P(\Delta _p(k))-P(\Delta _p(k-1))$
and
$\sigma \in P(\Delta _p(k))-P(\Delta _p(k-1))$
and
![]() $\tau \in P(\Delta _p(k-1))$
, if
$\tau \in P(\Delta _p(k-1))$
, if
![]() $\sigma>\tau $
, then
$\sigma>\tau $
, then
![]() $|W(\tau )|/|W(\sigma )|\equiv 0\mod p$
, implying that
$|W(\tau )|/|W(\sigma )|\equiv 0\mod p$
, implying that
![]() $\partial \widehat {\alpha }_k$
is actually a linear combination of simplices in
$\partial \widehat {\alpha }_k$
is actually a linear combination of simplices in
![]() $P(\Delta _p(k))-P(\Delta _p(k-1))$
. Thus, since
$P(\Delta _p(k))-P(\Delta _p(k-1))$
. Thus, since
![]() $\partial \widehat {\alpha }=0$
, we get
$\partial \widehat {\alpha }=0$
, we get
for each k. Let
 $$\begin{align*}\alpha_k=\sum_{\sigma\in P(\Delta_p(k))-P(\Delta_p(k-1))}\frac{p^{r-k}}{|W(\sigma)|}a_\sigma\sigma\in\widetilde{C}_*(\Delta_p(k);{\mathbb{Z}}/p). \end{align*}$$
$$\begin{align*}\alpha_k=\sum_{\sigma\in P(\Delta_p(k))-P(\Delta_p(k-1))}\frac{p^{r-k}}{|W(\sigma)|}a_\sigma\sigma\in\widetilde{C}_*(\Delta_p(k);{\mathbb{Z}}/p). \end{align*}$$
Then
![]() $\phi _k(\alpha _k)=\widehat {\alpha }_k$
, implying
$\phi _k(\alpha _k)=\widehat {\alpha }_k$
, implying
![]() $\partial \phi _k(\alpha _k)=0$
. So we get
$\partial \phi _k(\alpha _k)=0$
. So we get
![]() $\partial \alpha _k\in \widetilde {C}_*(\Delta _p(k-1);{\mathbb {Z}}/p)$
. Since
$\partial \alpha _k\in \widetilde {C}_*(\Delta _p(k-1);{\mathbb {Z}}/p)$
. Since
![]() $\widetilde {H}_*(\Delta _p(k-1);{\mathbb {Z}}/p)=0$
, there is
$\widetilde {H}_*(\Delta _p(k-1);{\mathbb {Z}}/p)=0$
, there is
![]() $\beta _k\in \widetilde {C}_*(\Delta _p(k-1);{\mathbb {Z}}/p)$
such that
$\beta _k\in \widetilde {C}_*(\Delta _p(k-1);{\mathbb {Z}}/p)$
such that
![]() $\partial \alpha _k=\partial \beta _k$
. Then, since the map
$\partial \alpha _k=\partial \beta _k$
. Then, since the map
![]() $\phi _k$
annihilates
$\phi _k$
annihilates
![]() $C_*(\Delta _p(k-1);{\mathbb {Z}}/p)$
, we get
$C_*(\Delta _p(k-1);{\mathbb {Z}}/p)$
, we get
So since
![]() $\widetilde {H}_*(\Delta _p(k-1);{\mathbb {Z}}/p)=0$
,
$\widetilde {H}_*(\Delta _p(k-1);{\mathbb {Z}}/p)=0$
,
![]() $\alpha _k-\beta _k$
is a boundary, implying
$\alpha _k-\beta _k$
is a boundary, implying
![]() $\widehat {\alpha }_k$
is a boundary. Thus, since k is arbitrary,
$\widehat {\alpha }_k$
is a boundary. Thus, since k is arbitrary,
![]() $\widehat {\alpha }$
is a boundary, which is a contradiction. Therefore,
$\widehat {\alpha }$
is a boundary, which is a contradiction. Therefore,
![]() $\operatorname {hocolim}\widehat {F}_2$
does not have p-torsion in homology, completing the proof.
$\operatorname {hocolim}\widehat {F}_2$
does not have p-torsion in homology, completing the proof.
Corollary 6.4 If the mod p homology of
![]() $\Delta _p(k)$
is nontrivial for some k, then
$\Delta _p(k)$
is nontrivial for some k, then
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
has p-torsion in homology for each
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
has p-torsion in homology for each
![]() $m\ge 2$
.
$m\ge 2$
.
Proof By Theorem 6.3, if the mod p homology of
![]() $\Delta _p(k)$
is nontrivial for some k, then
$\Delta _p(k)$
is nontrivial for some k, then
![]() $\operatorname {hocolim}\widehat {F}_2$
has p-torsion in homology. Thus, by Proposition 4.9,
$\operatorname {hocolim}\widehat {F}_2$
has p-torsion in homology. Thus, by Proposition 4.9,
![]() $\operatorname {Hom}({\mathbb {Z}}^2,G)_1$
has p-torsion in homology too. Since
$\operatorname {Hom}({\mathbb {Z}}^2,G)_1$
has p-torsion in homology too. Since
![]() $\operatorname {Hom}({\mathbb {Z}}^2,G)_1$
is a retract of
$\operatorname {Hom}({\mathbb {Z}}^2,G)_1$
is a retract of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
for
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
for
![]() $m\ge 2$
, the statement is proved.
$m\ge 2$
, the statement is proved.
7 Computation of torsion in homology
This section computes torsion in the homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
when G is
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
when G is
![]() $SU(n),\,Spin(2n)$
and exceptional groups by describing the complex
$SU(n),\,Spin(2n)$
and exceptional groups by describing the complex
![]() $\Delta _p(k)$
in terms of the extended Dynkin diagram of G.
$\Delta _p(k)$
in terms of the extended Dynkin diagram of G.
Note that every facet of
![]() $\Delta $
corresponds to a simple root or the highest root, and every i-face is an intersection of
$\Delta $
corresponds to a simple root or the highest root, and every i-face is an intersection of
![]() $n-i$
facets, where a facet of
$n-i$
facets, where a facet of
![]() $\Delta $
means a face of codimension one. Then there is a one-to-one correspondence between i-faces of
$\Delta $
means a face of codimension one. Then there is a one-to-one correspondence between i-faces of
![]() $\Delta $
and choices of
$\Delta $
and choices of
![]() $n-i$
roots from the simple roots and the highest root. Recall that the extended Dynkin diagram of G is a graph whose vertices are simple roots and the highest root. We will mean by a colored extended Dynkin diagram of G an extended Dynkin diagram of G whose vertices are colored by black and white. Here is an example of a colored extended Dynkin diagram of
$n-i$
roots from the simple roots and the highest root. Recall that the extended Dynkin diagram of G is a graph whose vertices are simple roots and the highest root. We will mean by a colored extended Dynkin diagram of G an extended Dynkin diagram of G whose vertices are colored by black and white. Here is an example of a colored extended Dynkin diagram of
![]() $Spin(12)$
.
$Spin(12)$
.

Let
![]() $\mathbb {D}_i$
be the set of all colored extended Dynkin diagram with
$\mathbb {D}_i$
be the set of all colored extended Dynkin diagram with
![]() $i+1$
white vertices and
$i+1$
white vertices and
![]() $n-i$
black vertices, where the extended Dynkin diagram of G has
$n-i$
black vertices, where the extended Dynkin diagram of G has
![]() $n+1$
vertices. Then, by the observation above, we get the following.
$n+1$
vertices. Then, by the observation above, we get the following.
Lemma 7.1 There is a bijection
which sends an i-face
![]() $\sigma \in P_i(\Delta )$
to a colored extended Dynkin diagram such that
$\sigma \in P_i(\Delta )$
to a colored extended Dynkin diagram such that
![]() $n-i$
vertices corresponding to
$n-i$
vertices corresponding to
![]() $\sigma $
are black.
$\sigma $
are black.
We will compute the mod p homology of
![]() $\Delta _p(k)$
by specifying
$\Delta _p(k)$
by specifying
![]() $\Psi _i(P_i(\Delta _p(k)))$
. Let
$\Psi _i(P_i(\Delta _p(k)))$
. Let
![]() $\Gamma $
be a colored extended Dynkin diagram of G. For an induced subgraph
$\Gamma $
be a colored extended Dynkin diagram of G. For an induced subgraph
![]() $\Theta $
of
$\Theta $
of
![]() $\Gamma $
, let
$\Gamma $
, let
![]() $W_\Theta $
denote the subgroup of W generated by simple reflections corresponding to the vertices of
$W_\Theta $
denote the subgroup of W generated by simple reflections corresponding to the vertices of
![]() $\Theta $
, where we put
$\Theta $
, where we put
![]() $W_\emptyset =1$
. By definition, we have the following.
$W_\emptyset =1$
. By definition, we have the following.
Lemma 7.2
-
(1) If a colored extended Dynkin diagram
 $\Gamma $
is the disjoint union of induced subgraphs
$\Gamma $
is the disjoint union of induced subgraphs
 $\Gamma _1,\ldots ,\Gamma _k$
after removing all white vertices, then
$\Gamma _1,\ldots ,\Gamma _k$
after removing all white vertices, then  $$\begin{align*}W_\Gamma=W_{\Gamma_1}\times\cdots\times W_{\Gamma_k}. \end{align*}$$
$$\begin{align*}W_\Gamma=W_{\Gamma_1}\times\cdots\times W_{\Gamma_k}. \end{align*}$$
-
(2) For an i-face
 $\sigma $
of
$\sigma $
of
 $\Delta $
, there is an isomorphism
$\Delta $
, there is an isomorphism  $$\begin{align*}W(\sigma)\cong W_{\Psi_i(\sigma)}. \end{align*}$$
$$\begin{align*}W(\sigma)\cong W_{\Psi_i(\sigma)}. \end{align*}$$
Let
![]() $v_1,\ldots ,v_i$
be vertices of the extended Dynkin diagram. We denote by
$v_1,\ldots ,v_i$
be vertices of the extended Dynkin diagram. We denote by
![]() $v_1\ldots v_i$
an
$v_1\ldots v_i$
an
![]() $(i-1)$
-face
$(i-1)$
-face
![]() $\sigma $
such that white vertices of the extended Dynkin diagram
$\sigma $
such that white vertices of the extended Dynkin diagram
![]() $\Psi _{i-1}(\sigma )$
are
$\Psi _{i-1}(\sigma )$
are
![]() $v_1,\ldots ,v_i$
. For example, as for
$v_1,\ldots ,v_i$
. For example, as for
![]() $G=SU(3)$
, 13 corresponds the following colored extended Dynkin diagram.
$G=SU(3)$
, 13 corresponds the following colored extended Dynkin diagram.

7.1 The
 $SU(n)$
case
$SU(n)$
case
Throughout this subsection, let
![]() $G=SU(n+1)$
. Recall that the extended Dynkin diagram of
$G=SU(n+1)$
. Recall that the extended Dynkin diagram of
![]() $SU(n+1)$
is the cycle graph with
$SU(n+1)$
is the cycle graph with
![]() $n+1$
vertices, denoted by
$n+1$
vertices, denoted by
![]() $C_{n+1}$
.
$C_{n+1}$
.
Example 7.3 The following figure shows all colored extended Dynkin diagrams of
![]() $SU(3)$
, where
$SU(3)$
, where
![]() $\Delta $
is a 2-simplex. The left three graphs correspond to vertices, the middle three graphs correspond to edges, and the most right graph corresponds to the 2-simplex.
$\Delta $
is a 2-simplex. The left three graphs correspond to vertices, the middle three graphs correspond to edges, and the most right graph corresponds to the 2-simplex.

Now, we describe faces of
![]() $\Delta _p(0)$
. Let
$\Delta _p(0)$
. Let
![]() $C(i)$
be the following graph with
$C(i)$
be the following graph with
![]() $p^i-1$
black vertices and one gray vertex.
$p^i-1$
black vertices and one gray vertex.
Proposition 7.4 For
![]() $n>1$
, let
$n>1$
, let
![]() $n+1=\sum _{j=0}^la_jp^j$
be the p-adic expansion, where
$n+1=\sum _{j=0}^la_jp^j$
be the p-adic expansion, where
![]() $0\le a_j<p$
for each j. A colored extended Dynkin diagram of
$0\le a_j<p$
for each j. A colored extended Dynkin diagram of
![]() $SU(n+1)$
is in
$SU(n+1)$
is in
![]() $\Psi _i(P_i(\Delta _p(0)))$
if and only if it is obtained by gluing
$\Psi _i(P_i(\Delta _p(0)))$
if and only if it is obtained by gluing
![]() $a_j$
copies of
$a_j$
copies of
![]() $C(j)$
for
$C(j)$
for
![]() $j=0,\ldots ,l$
such that
$j=0,\ldots ,l$
such that
![]() $i+1$
gray vertices are replaced by white vertices and the remaining gray vertices are replaced by black vertices.
$i+1$
gray vertices are replaced by white vertices and the remaining gray vertices are replaced by black vertices.
Proof First, we prove the if part. Let
![]() $\Gamma $
be the colored extended Dynkin diagram specified in the statement, and let
$\Gamma $
be the colored extended Dynkin diagram specified in the statement, and let
![]() $\Gamma '$
be a colored extended Dynkin diagram which is constructed by recoloring the originally gray vertices of
$\Gamma '$
be a colored extended Dynkin diagram which is constructed by recoloring the originally gray vertices of
![]() $\Gamma $
by white. Then, by Lemma 7.2,
$\Gamma $
by white. Then, by Lemma 7.2,
 $$\begin{align*}|W_{\Gamma'}|=\prod_{j=0}^l(p^j!)^{a_j}, \end{align*}$$
$$\begin{align*}|W_{\Gamma'}|=\prod_{j=0}^l(p^j!)^{a_j}, \end{align*}$$
and so we get
 $$\begin{align*}\frac{|W|}{|W_{\Gamma'}|}=\prod_{j=1}^{l}\prod_{j'=1}^{a_j-1}\binom{n+1-j'p^j\sum_{k>j}a_kp^k}{p^j}. \end{align*}$$
$$\begin{align*}\frac{|W|}{|W_{\Gamma'}|}=\prod_{j=1}^{l}\prod_{j'=1}^{a_j-1}\binom{n+1-j'p^j\sum_{k>j}a_kp^k}{p^j}. \end{align*}$$
By Lucas’s theorem,
![]() $\binom {n+1-j'p^j\sum _{k>j}a_kp^k}{p^j}$
is prime to p for each j and
$\binom {n+1-j'p^j\sum _{k>j}a_kp^k}{p^j}$
is prime to p for each j and
![]() $j'$
, implying that
$j'$
, implying that
![]() $\frac {|W|}{|W_{\Gamma '}|}$
is prime to p. Then, since
$\frac {|W|}{|W_{\Gamma '}|}$
is prime to p. Then, since
![]() $|W_{\Gamma '}|$
divides
$|W_{\Gamma '}|$
divides
![]() $|W_\Gamma |$
,
$|W_\Gamma |$
,
![]() $\frac {|W|}{|W_{\Gamma }|}$
is prime to p, so that we obtain
$\frac {|W|}{|W_{\Gamma }|}$
is prime to p, so that we obtain
![]() $\Gamma \in \Psi _i(P_i(\Delta _p(0)))$
.
$\Gamma \in \Psi _i(P_i(\Delta _p(0)))$
.
Next, we prove the only if part. The
![]() $n=2$
case can be easily deduced from Example 7.3. Suppose we have the one-to-one correspondence in the statement for
$n=2$
case can be easily deduced from Example 7.3. Suppose we have the one-to-one correspondence in the statement for
![]() $SU(k+1)$
with
$SU(k+1)$
with
![]() $k\le n-1$
. Since
$k\le n-1$
. Since
![]() $W(v)=W$
for each vertex v of
$W(v)=W$
for each vertex v of
![]() $\Delta $
, vertices of
$\Delta $
, vertices of
![]() $\Delta $
are vertices of
$\Delta $
are vertices of
![]() $\Delta _p(0)$
. Then, by Lemma 7.1, there is a one-to-one correspondence between
$\Delta _p(0)$
. Then, by Lemma 7.1, there is a one-to-one correspondence between
![]() $\Psi _0(P_0(\Delta _p(0)))$
and vertices of
$\Psi _0(P_0(\Delta _p(0)))$
and vertices of
![]() $\Delta _p(0)$
.
$\Delta _p(0)$
.
Let
![]() $\Gamma \in \Psi _i(P_i(\Delta _p(0)))$
for
$\Gamma \in \Psi _i(P_i(\Delta _p(0)))$
for
![]() $i>0$
. Then
$i>0$
. Then
![]() $\Gamma $
includes the following subgraph
$\Gamma $
includes the following subgraph
![]() $\Theta $
with
$\Theta $
with
![]() $n'$
black vertices and two white vertices for
$n'$
black vertices and two white vertices for
![]() $0\le n'\le n-2$
.
$0\le n'\le n-2$
.
Let
![]() $n'+1=\sum _{j=0}^la_j'p^j$
be the p-adic expansion. By Lemma 7.2,
$n'+1=\sum _{j=0}^la_j'p^j$
be the p-adic expansion. By Lemma 7.2,
such that
![]() $|W_\Theta |=(n'+1)!$
and
$|W_\Theta |=(n'+1)!$
and
![]() $|W_{\Gamma -\Theta }|$
divides
$|W_{\Gamma -\Theta }|$
divides
![]() $(n-n')!$
. Then, since
$(n-n')!$
. Then, since
![]() $|W|/|W_\Gamma |$
is prime to p,
$|W|/|W_\Gamma |$
is prime to p,
 $$\begin{align*}\frac{|W|}{(n'+1)!(n-n')!}=\frac{(n+1)!}{(n'+1)!(n-n')!}=\binom{n+1}{n'+1} \end{align*}$$
$$\begin{align*}\frac{|W|}{(n'+1)!(n-n')!}=\frac{(n+1)!}{(n'+1)!(n-n')!}=\binom{n+1}{n'+1} \end{align*}$$
is also prime to p. Thus, by Lucas’s theorem, we obtain
for each j. Let
![]() $\overline {\Theta }$
be a cycle graph with
$\overline {\Theta }$
be a cycle graph with
![]() $n-n'+1$
vertices which is obtained from
$n-n'+1$
vertices which is obtained from
![]() $\Gamma $
by contracting
$\Gamma $
by contracting
![]() $\Theta $
to a single white vertex. Then, by the induction hypothesis,
$\Theta $
to a single white vertex. Then, by the induction hypothesis,
![]() $\overline {\Theta }$
belongs to
$\overline {\Theta }$
belongs to
![]() $\Psi _{i-1}(\Delta _p(0))$
for
$\Psi _{i-1}(\Delta _p(0))$
for
![]() $G=SU(n-n')$
, and so
$G=SU(n-n')$
, and so
![]() $\overline {\Theta }$
is obtained by gluing
$\overline {\Theta }$
is obtained by gluing
![]() $C(j)$
. By definition, the graph
$C(j)$
. By definition, the graph
![]() $\Theta $
is also obtained by gluing
$\Theta $
is also obtained by gluing
![]() $C(j)$
. Therefore,
$C(j)$
. Therefore,
![]() $\Gamma $
itself is obtained by gluing
$\Gamma $
itself is obtained by gluing
![]() $C(j)$
, completing the proof.
$C(j)$
, completing the proof.
Now, we compute torsion in the homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,SU(n+1))_1$
.
$\operatorname {Hom}({\mathbb {Z}}^m,SU(n+1))_1$
.
Theorem 7.5 The homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,SU(n+1))_1$
for
$\operatorname {Hom}({\mathbb {Z}}^m,SU(n+1))_1$
for
![]() $m\ge 2$
has p-torsion in homology if and only if
$m\ge 2$
has p-torsion in homology if and only if
![]() $p\le n+1$
.
$p\le n+1$
.
Proof By Lemma 1.1 and
![]() $|W|=(n+1)!$
,
$|W|=(n+1)!$
,
![]() $\operatorname {Hom}({\mathbb {Z}}^m,SU(n+1))_1$
has no p-torsion in homology for
$\operatorname {Hom}({\mathbb {Z}}^m,SU(n+1))_1$
has no p-torsion in homology for
![]() $p>n+1$
. So we assume
$p>n+1$
. So we assume
![]() $p\le n+1$
and prove that
$p\le n+1$
and prove that
![]() $\operatorname {Hom}({\mathbb {Z}}^m,SU(n+1))_1$
has p-torsion in homology. By Corollary 6.4, it suffices to show that the mod p homology of
$\operatorname {Hom}({\mathbb {Z}}^m,SU(n+1))_1$
has p-torsion in homology. By Corollary 6.4, it suffices to show that the mod p homology of
![]() $\Delta _p(0)$
for
$\Delta _p(0)$
for
![]() $SU(n+1)$
is nontrivial. To this end, we aim to prove
$SU(n+1)$
is nontrivial. To this end, we aim to prove
![]() $\chi (\Delta _p(0))\ne 1$
, where
$\chi (\Delta _p(0))\ne 1$
, where
![]() $\chi (K)$
denotes the Euler characteristic of a simplicial complex K. By Lemma 7.1 and Proposition 7.4, rotations of a cycle graph induce the action of a cyclic group
$\chi (K)$
denotes the Euler characteristic of a simplicial complex K. By Lemma 7.1 and Proposition 7.4, rotations of a cycle graph induce the action of a cyclic group
![]() ${\mathbb {Z}}/(n+1)$
on
${\mathbb {Z}}/(n+1)$
on
![]() $\Psi _i(P_i(\Delta _p(0)))$
. Let
$\Psi _i(P_i(\Delta _p(0)))$
. Let
![]() $n+1=\sum _{j=0}^la_jp^j$
be the p-adic expansion, where
$n+1=\sum _{j=0}^la_jp^j$
be the p-adic expansion, where
![]() $a_l\ne 0$
. Then every element of the stabilizer of a face
$a_l\ne 0$
. Then every element of the stabilizer of a face
![]() $\sigma \in P_i(\Delta _p(0))$
permutes
$\sigma \in P_i(\Delta _p(0))$
permutes
![]() $C(l)$
-parts of
$C(l)$
-parts of
![]() $\Psi _i(\sigma )$
because
$\Psi _i(\sigma )$
because
![]() $C(l)$
is not obtained by gluing
$C(l)$
is not obtained by gluing
![]() $a_i$
copies of
$a_i$
copies of
![]() $C(i)$
for
$C(i)$
for
![]() $i<l$
. Thus, the order of the stabilizer of
$i<l$
. Thus, the order of the stabilizer of
![]() $\Psi _i(\sigma )$
is at most
$\Psi _i(\sigma )$
is at most
![]() $(n+1,a_l)$
, implying
$(n+1,a_l)$
, implying
![]() $|P_i(\Delta _p(0))|$
is divisible by
$|P_i(\Delta _p(0))|$
is divisible by
for each i. Therefore, since
![]() $a_l<n+1$
and
$a_l<n+1$
and
![]() $\chi (\Delta _p(0))=\sum _{i\ge 0}(-1)^i|P_i(\Delta _p(0))|$
, we obtain that
$\chi (\Delta _p(0))=\sum _{i\ge 0}(-1)^i|P_i(\Delta _p(0))|$
, we obtain that
![]() $\chi (\Delta _p(0))$
is divisible by
$\chi (\Delta _p(0))$
is divisible by
![]() $\frac {n+1}{(n+1,a_l)}$
, implying
$\frac {n+1}{(n+1,a_l)}$
, implying
![]() $\chi (\Delta _p(0))\ne 1$
.
$\chi (\Delta _p(0))\ne 1$
.
7.2 The
 $\boldsymbol{Spin(2n)}$
case
$\boldsymbol{Spin(2n)}$
case
Throughout this subsection, let
![]() $G=Spin(2n)$
, and let r be the integer such that
$G=Spin(2n)$
, and let r be the integer such that
![]() $|W|=p^rq$
for
$|W|=p^rq$
for
![]() $(p,q)=1$
. We aim to prove the non-triviality of the homology of
$(p,q)=1$
. We aim to prove the non-triviality of the homology of
![]() $\Delta _p(r-1)$
. Fix a vertex v of the extended Dynkin diagram of
$\Delta _p(r-1)$
. Fix a vertex v of the extended Dynkin diagram of
![]() $SU(n+1)$
. Let
$SU(n+1)$
. Let
![]() $f_i(n,p)$
denote the number of colored extended Dynkin diagrams
$f_i(n,p)$
denote the number of colored extended Dynkin diagrams
![]() $\Gamma $
of
$\Gamma $
of
![]() $SU(n+1)$
such that
$SU(n+1)$
such that
![]() $\Gamma \in \mathbb {D}_i$
, v is white-colored and
$\Gamma \in \mathbb {D}_i$
, v is white-colored and
![]() $|W_\Gamma |$
is prime to p. Let
$|W_\Gamma |$
is prime to p. Let
 $$\begin{align*}\chi(n,p)=\sum_{i=0}^n(-1)^if_i(n,p). \end{align*}$$
$$\begin{align*}\chi(n,p)=\sum_{i=0}^n(-1)^if_i(n,p). \end{align*}$$
Example 7.6 All colored extended Dynkin diagrams
![]() $\Gamma $
of
$\Gamma $
of
![]() $SU(4)$
satisfying that a fixed vertex v is white-colored and
$SU(4)$
satisfying that a fixed vertex v is white-colored and
![]() $|W_\Gamma |$
is prime to
$|W_\Gamma |$
is prime to
![]() $p=3$
are as below. Then
$p=3$
are as below. Then
![]() $f_0=0,\,f_1=1,\,f_2=3,\,f_3=1$
, implying
$f_0=0,\,f_1=1,\,f_2=3,\,f_3=1$
, implying
![]() $\chi (3,3)=1$
.
$\chi (3,3)=1$
.

We compute
![]() $\chi (n,p)$
for general n and p.
$\chi (n,p)$
for general n and p.
Lemma 7.7 We have
 $$\begin{align*}\chi(n,p)= \begin{cases} -1,&n\equiv-1\quad\mod p,\\ 1,&n\equiv 0\quad\mod p,\\ 0,&\text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\chi(n,p)= \begin{cases} -1,&n\equiv-1\quad\mod p,\\ 1,&n\equiv 0\quad\mod p,\\ 0,&\text{otherwise.} \end{cases} \end{align*}$$
Proof It is easy to see the statement holds for
![]() $n\le p-1$
. Let
$n\le p-1$
. Let
![]() $\Gamma $
be a colored extended Dynkin diagram of
$\Gamma $
be a colored extended Dynkin diagram of
![]() $SU(n+1)$
such that v is white-colored and
$SU(n+1)$
such that v is white-colored and
![]() $|W_\Gamma |$
is prime to p. Then for
$|W_\Gamma |$
is prime to p. Then for
![]() $n\ge p$
, it follows from Lemma 7.2 that
$n\ge p$
, it follows from Lemma 7.2 that
![]() $\Gamma $
is given as below, where
$\Gamma $
is given as below, where
![]() $0\le k\le p-2$
.
$0\le k\le p-2$
.

Thus, we get
 $$\begin{align*}\chi(n,p)=\sum_{i=1}^{p-2}-\chi(n-i,p), \end{align*}$$
$$\begin{align*}\chi(n,p)=\sum_{i=1}^{p-2}-\chi(n-i,p), \end{align*}$$
and so the proof is done by induction on n.
We name the vertices of the extended Dynkin diagram of
![]() $Spin(2n)$
as follows.
$Spin(2n)$
as follows.

Let
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
be colored extended Dynkin diagrams of
$\Gamma _2$
be colored extended Dynkin diagrams of
![]() $Spin(2n)$
. Suppose all but one vertices of
$Spin(2n)$
. Suppose all but one vertices of
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
have the same colors. If
$\Gamma _2$
have the same colors. If
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
correspond to faces of
$\Gamma _2$
correspond to faces of
![]() $\Delta _p(k)$
, then we can cancel out these faces in the computation of
$\Delta _p(k)$
, then we can cancel out these faces in the computation of
![]() $\chi (\Delta _p(k))$
. Thus, we specify the case
$\chi (\Delta _p(k))$
. Thus, we specify the case
![]() $\Gamma _1$
is a face of
$\Gamma _1$
is a face of
![]() $\Delta _p(k)$
but
$\Delta _p(k)$
but
![]() $\Gamma _2$
is not.
$\Gamma _2$
is not.
Lemma 7.8 Let
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
be colored extended Dynkin diagrams of
$\Gamma _2$
be colored extended Dynkin diagrams of
![]() $Spin(2n)$
such that all vertices but the vertex
$Spin(2n)$
such that all vertices but the vertex
![]() $v_1$
have the same color. If
$v_1$
have the same color. If
![]() $\Gamma _1$
corresponds to a face of
$\Gamma _1$
corresponds to a face of
![]() $\Delta _p(r-1)$
and
$\Delta _p(r-1)$
and
![]() $\Gamma _2$
is not, then
$\Gamma _2$
is not, then
![]() $\Gamma _2$
is of the following form.
$\Gamma _2$
is of the following form.

Proof The statement follows from Lemma 7.2.
Theorem 7.9 If
![]() $p\le n$
and
$p\le n$
and
![]() $n\equiv 0,1\quad\mod p$
, then for
$n\equiv 0,1\quad\mod p$
, then for
![]() $m\ge 2$
,
$m\ge 2$
,
![]() $\operatorname {Hom}({\mathbb {Z}}^m,Spin(2n))_1$
has p-torsion in homology.
$\operatorname {Hom}({\mathbb {Z}}^m,Spin(2n))_1$
has p-torsion in homology.
Proof As in the proof of Theorem 7.5, it suffices to show
![]() $\chi (\Delta _p(r-1))\ne 1$
for
$\chi (\Delta _p(r-1))\ne 1$
for
![]() $p\le n$
and
$p\le n$
and
![]() $n\equiv 0,1\mod p$
. Let
$n\equiv 0,1\mod p$
. Let
 $$\begin{align*}\widetilde{\chi}(n,p)=\sum_{i=0}^n(-1)^i(|P_i(\Delta)|-|P_i(\Delta_p(r-1))|). \end{align*}$$
$$\begin{align*}\widetilde{\chi}(n,p)=\sum_{i=0}^n(-1)^i(|P_i(\Delta)|-|P_i(\Delta_p(r-1))|). \end{align*}$$
Then, since
![]() $\chi (\Delta )=1$
, we have
$\chi (\Delta )=1$
, we have
![]() $\chi (\Delta _p(r-1))=1-\widetilde {\chi }(n,p)$
, and so
$\chi (\Delta _p(r-1))=1-\widetilde {\chi }(n,p)$
, and so
![]() $\chi (\Delta _p(r-1))\ne 1$
if and only if
$\chi (\Delta _p(r-1))\ne 1$
if and only if
![]() $\widetilde {\chi }(n,p)\ne 0$
.
$\widetilde {\chi }(n,p)\ne 0$
.
First, we consider the
![]() $n\ge 2p+2$
case. Note that Lemma 7.8 holds if we replace
$n\ge 2p+2$
case. Note that Lemma 7.8 holds if we replace
![]() $v_1$
with
$v_1$
with
![]() $v_n$
. Then, since
$v_n$
. Then, since
![]() $n\ge 2p+2$
, we only need to count colored extended Dynkin diagrams of
$n\ge 2p+2$
, we only need to count colored extended Dynkin diagrams of
![]() $Spin(2n)$
such that vertices
$Spin(2n)$
such that vertices
![]() $v_1,v_2,\ldots ,v_{p+1},v_{n-p+1},v_{n-p+2},\ldots ,v_{n+1}$
are colored as in Lemma 7.8. If we delete
$v_1,v_2,\ldots ,v_{p+1},v_{n-p+1},v_{n-p+2},\ldots ,v_{n+1}$
are colored as in Lemma 7.8. If we delete
![]() $v_1,v_2,\ldots ,v_{p+1},v_{n-p+1},v_{n-p+2},\ldots ,v_{n+1}$
and add a white vertex v together with edges
$v_1,v_2,\ldots ,v_{p+1},v_{n-p+1},v_{n-p+2},\ldots ,v_{n+1}$
and add a white vertex v together with edges
![]() $vv_{p+2}$
and
$vv_{p+2}$
and
![]() $vv_{n-p}$
, then we get a colored extended Dynkin diagram of
$vv_{n-p}$
, then we get a colored extended Dynkin diagram of
![]() $SU(n-2p)$
. Through this operation, there is a one-to-one correspondence between colored extended Dynkin diagrams of
$SU(n-2p)$
. Through this operation, there is a one-to-one correspondence between colored extended Dynkin diagrams of
![]() $Spin(2n)$
whose left and right ends are as in Lemma 7.8 and colored extended Dynkin diagrams of
$Spin(2n)$
whose left and right ends are as in Lemma 7.8 and colored extended Dynkin diagrams of
![]() $SU(n-2p)$
such that a fixed vertex v is white-colored. Then we get
$SU(n-2p)$
such that a fixed vertex v is white-colored. Then we get
Therefore, for
![]() $n\ge 2p+2$
, the proof is finished by Lemma 7.7.
$n\ge 2p+2$
, the proof is finished by Lemma 7.7.
Next, we consider the
![]() $p\le n<2p+2$
case. We only need to count colored extended Dynkin diagrams such that vertices
$p\le n<2p+2$
case. We only need to count colored extended Dynkin diagrams such that vertices
![]() $v_1,v_2,\ldots ,v_{p+1}$
are colored as in Lemma 7.8. Except for
$v_1,v_2,\ldots ,v_{p+1}$
are colored as in Lemma 7.8. Except for
![]() $n=p,p+1,2p,2p+1$
, vertices
$n=p,p+1,2p,2p+1$
, vertices
![]() $v_{p+2},v_{p+3},\ldots ,v_{n+1}$
can have arbitrarily color, and so
$v_{p+2},v_{p+3},\ldots ,v_{n+1}$
can have arbitrarily color, and so
![]() $\widetilde {\chi }(n,p)=0$
. For
$\widetilde {\chi }(n,p)=0$
. For
![]() $n=p$
, we only need to count the graphs whose vertices
$n=p$
, we only need to count the graphs whose vertices
![]() $v_1,\ldots ,v_{p-1}$
are colored as in Lemma 7.8. Then there are only three graphs to be counted as follows, where
$v_1,\ldots ,v_{p-1}$
are colored as in Lemma 7.8. Then there are only three graphs to be counted as follows, where
![]() $v_p$
and
$v_p$
and
![]() $v_{p+1}$
are either black or white such that they cannot be white at the same time.
$v_{p+1}$
are either black or white such that they cannot be white at the same time.

In each case
![]() $n=p+1,2p,2p+1$
, it follows from Lemma 7.8 that there is only one graph to be counted. For
$n=p+1,2p,2p+1$
, it follows from Lemma 7.8 that there is only one graph to be counted. For
![]() $n=p+1$
, the end vertices
$n=p+1$
, the end vertices
![]() $v_1,v_2,v_{p+1},v_{p+2}$
are white and the remaining vertices are black. For
$v_1,v_2,v_{p+1},v_{p+2}$
are white and the remaining vertices are black. For
![]() $n=2p$
, the end vertices
$n=2p$
, the end vertices
![]() $v_1,v_2,v_{2p},v_{2p+1}$
and the middle vertex
$v_1,v_2,v_{2p},v_{2p+1}$
and the middle vertex
![]() $v_{p+1}$
are white and the remaining vertices are black. For
$v_{p+1}$
are white and the remaining vertices are black. For
![]() $n=2p+1$
, the end vertices
$n=2p+1$
, the end vertices
![]() $v_1,v_2,v_{2p+1},v_{2p+2}$
and the middle vertices
$v_1,v_2,v_{2p+1},v_{2p+2}$
and the middle vertices
![]() $v_{p+1},v_{p+2}$
are white and the remaining vertices are black. Summarizing,
$v_{p+1},v_{p+2}$
are white and the remaining vertices are black. Summarizing,
![]() $\widetilde {\chi }(n,p)\ne 0$
for
$\widetilde {\chi }(n,p)\ne 0$
for
![]() $n=p,p+1,2p,2p+1$
. Therefore the statement is proved.
$n=p,p+1,2p,2p+1$
. Therefore the statement is proved.
7.3 The exceptional case
We continue to compute torsion in the homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
when G is the exceptional Lie group. Let G be exceptional, and let p be a prime dividing
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
when G is the exceptional Lie group. Let G be exceptional, and let p be a prime dividing
![]() $|W|$
, where
$|W|$
, where
![]() $|W|$
is given as in Table 1. Then G has p-torsion in homology except for
$|W|$
is given as in Table 1. Then G has p-torsion in homology except for
(see [Reference Mimura and Toda23, Theorem 5.11, Chapter 7]). Since G is a retract of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
,
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
,
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
has p-torsion in homology except possibly for the cases (7.1). On the other hand,
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
has p-torsion in homology except possibly for the cases (7.1). On the other hand,
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
has no p-torsion in homology when p does not divide
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
has no p-torsion in homology when p does not divide
![]() $|W|$
. Then we only need to consider the cases (7.1).
$|W|$
. Then we only need to consider the cases (7.1).
Table 1: Simple Lie groups and their Weyl groups.

Now, we prove the following.
Theorem 7.10 Let G be exceptional. Then
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
for
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
for
![]() $m\ge 2$
has p-torsion in homology if and only if p divides
$m\ge 2$
has p-torsion in homology if and only if p divides
![]() $|W|$
, except possibly for
$|W|$
, except possibly for
![]() $(G,p)=(E_7,5),(E_7,7),(E_8,7)$
.
$(G,p)=(E_7,5),(E_7,7),(E_8,7)$
.
Proof As observed above, it follows from Corollary 6.4 that we only need to show that
![]() $\Delta _p(0)$
has nontrivial mod p homology for
$\Delta _p(0)$
has nontrivial mod p homology for
![]() $(G,p)$
in (7.1) for
$(G,p)$
in (7.1) for
![]() $(G,p)=(G_2,3),(E_6,5)$
.
$(G,p)=(G_2,3),(E_6,5)$
.
Let
![]() $G=G_2$
. Then the extended Dynkin diagram is given as below. So, by Lemma 7.2,
$G=G_2$
. Then the extended Dynkin diagram is given as below. So, by Lemma 7.2,
![]() $\Delta _3(0)$
consists only of two vertices 1 and 3, implying it has nontrivial mod p homology.
$\Delta _3(0)$
consists only of two vertices 1 and 3, implying it has nontrivial mod p homology.
Let
![]() $G=E_6$
. Then the extended Dynkin diagram is given as below.
$G=E_6$
. Then the extended Dynkin diagram is given as below.

It has symmetry of rotation around the vertex v. By Lemma 7.2, we can see that if a colored extended Dynkin diagram is symmetric with respect to the rotation around v, then its corresponding face of
![]() $\Delta $
does not lie in
$\Delta $
does not lie in
![]() $\Delta _5(0)$
. Then the number of i-faces of
$\Delta _5(0)$
. Then the number of i-faces of
![]() $\Delta _5(0)$
is divisible by 3 for each i, implying
$\Delta _5(0)$
is divisible by 3 for each i, implying
![]() $\chi (\Delta _5(0))$
is divisible by 3. Thus,
$\chi (\Delta _5(0))$
is divisible by 3. Thus,
![]() $\Delta _5(0)$
has nontrivial mod 5 homology.
$\Delta _5(0)$
has nontrivial mod 5 homology.
By Theorems 7.5, 7.9, and 7.10, we dare to pose the following.
Conjecture 7.11 The homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
for
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
for
![]() $m\ge 2$
has p-torsion if and only if p divides the order of W.
$m\ge 2$
has p-torsion if and only if p divides the order of W.
8 Negative results
Although we have pose Conjecture 7.11, the complex
![]() $\Delta _p(k)$
does not work in the remaining cases, unfortunately. To be fair, we prove this, but we have to notice that those negative results do not imply the nonexistence of torsion in homology because the non-triviality of the homology of
$\Delta _p(k)$
does not work in the remaining cases, unfortunately. To be fair, we prove this, but we have to notice that those negative results do not imply the nonexistence of torsion in homology because the non-triviality of the homology of
![]() $\Delta _p(k)$
is only a sufficient condition for the existence of p-torsion in the homology of
$\Delta _p(k)$
is only a sufficient condition for the existence of p-torsion in the homology of
![]() $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
for
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$
for
![]() $m\ge 2$
.
$m\ge 2$
.
First, we consider the
![]() $Spin(2n)$
case by examining
$Spin(2n)$
case by examining
![]() $(G,p)=(Spin(10),3)$
which is not included in Theorem 7.9. Since
$(G,p)=(Spin(10),3)$
which is not included in Theorem 7.9. Since
![]() $|W|=2^4\cdot 5!$
for
$|W|=2^4\cdot 5!$
for
![]() $G=Spin(10)$
, we only need to consider
$G=Spin(10)$
, we only need to consider
![]() $\Delta _3(0)$
.
$\Delta _3(0)$
.
Proposition 8.1 The complex
![]() $\Delta _3(0)$
of
$\Delta _3(0)$
of
![]() $Spin(10)$
is contractible.
$Spin(10)$
is contractible.
Proof We prove the statement by applying discrete Morse theory. We refer to [Reference Kozlov22] for materials of discrete Morse theory. We name the vertices of the extended Dynkin diagram of
![]() $Spin(10)$
as follows.
$Spin(10)$
as follows.

By Lemma 7.2, it is straightforward to see that facets of
![]() $\Delta _3(0)$
are
$\Delta _3(0)$
are
Then we have the following acyclic partial matching.

Since all faces of
![]() $\Delta _3(0)$
but the vertex 6 appear in the acyclic partial matching above, it follows from the fundamental theorem of discrete Morse theory that
$\Delta _3(0)$
but the vertex 6 appear in the acyclic partial matching above, it follows from the fundamental theorem of discrete Morse theory that
![]() $\Delta _3(0)$
collapses onto the vertex 6, implying
$\Delta _3(0)$
collapses onto the vertex 6, implying
![]() $\Delta _3(0)$
is contractible.
$\Delta _3(0)$
is contractible.
Next, we consider the
![]() $G=Spin(2n+1),\,Sp(n)$
case.
$G=Spin(2n+1),\,Sp(n)$
case.
Proposition 8.2 Let G be
![]() $Spin(2n+1)$
for
$Spin(2n+1)$
for
![]() $n\geq 3$
or
$n\geq 3$
or
![]() $Sp(n)$
, and let p be an odd prime dividing
$Sp(n)$
, and let p be an odd prime dividing
![]() $|W|$
. Then for each k,
$|W|$
. Then for each k,
![]() $\Delta _p(k)$
is contractible.
$\Delta _p(k)$
is contractible.
Proof We only prove the case
![]() $G=Spin(2n+1)$
because the case
$G=Spin(2n+1)$
because the case
![]() $G=Sp(n)$
is quite similarly proved. The extended Dynkin diagram of
$G=Sp(n)$
is quite similarly proved. The extended Dynkin diagram of
![]() $Spin(2n+1)$
is given as follows.
$Spin(2n+1)$
is given as follows.

Let
![]() $\widehat {\Delta }_p(k)$
be the subcomplex of
$\widehat {\Delta }_p(k)$
be the subcomplex of
![]() $\Delta _p(k)$
consisting of faces
$\Delta _p(k)$
consisting of faces
![]() $\sigma $
such that in the corresponding colored extended Dynkin diagram, the vertex v is black. Let
$\sigma $
such that in the corresponding colored extended Dynkin diagram, the vertex v is black. Let
![]() $\Gamma =\Psi _i(\sigma )$
for an i-face
$\Gamma =\Psi _i(\sigma )$
for an i-face
![]() $\sigma $
of
$\sigma $
of
![]() $\widehat {\Delta }_p(k)$
. Let
$\widehat {\Delta }_p(k)$
. Let
![]() $\Gamma '$
be a colored extended diagram whose vertices have the same color as
$\Gamma '$
be a colored extended diagram whose vertices have the same color as
![]() $\Gamma $
except for the vertex v. So the vertex v of
$\Gamma $
except for the vertex v. So the vertex v of
![]() $\Gamma '$
is white. By Lemma 7.2,
$\Gamma '$
is white. By Lemma 7.2,
![]() $\Gamma '$
corresponds to the join
$\Gamma '$
corresponds to the join
![]() $v*\sigma $
. Since
$v*\sigma $
. Since
![]() $|W_{\Gamma }|/|W_{\Gamma '}|$
is a power of 2, the join
$|W_{\Gamma }|/|W_{\Gamma '}|$
is a power of 2, the join
![]() $v*\sigma $
is an
$v*\sigma $
is an
![]() $(i+1)$
-face of
$(i+1)$
-face of
![]() $\Delta _p(k)$
. Thus,
$\Delta _p(k)$
. Thus,
![]() $\Delta _p(k)$
is the join
$\Delta _p(k)$
is the join
![]() $v*\widehat {\Delta }_p(k)$
, completing the proof.
$v*\widehat {\Delta }_p(k)$
, completing the proof.
Finally, we consider the exceptional case. The only cases that are not included in Theorem 7.10 are
![]() $(G,p)=(E_7,5),(E_7,7),(E_8,7)$
. Since
$(G,p)=(E_7,5),(E_7,7),(E_8,7)$
. Since
![]() $|W(E_7)|=2^{10}\cdot 3^4\cdot 5\cdot 7$
, we only need to consider
$|W(E_7)|=2^{10}\cdot 3^4\cdot 5\cdot 7$
, we only need to consider
![]() $\Delta _p(0)$
for
$\Delta _p(0)$
for
![]() $G=E_7$
and
$G=E_7$
and
![]() $p=5,7$
.
$p=5,7$
.
Proposition 8.3 For
![]() $G=E_7$
and
$G=E_7$
and
![]() $p=5,7$
,
$p=5,7$
,
![]() $\Delta _p(0)$
is contractible.
$\Delta _p(0)$
is contractible.
Proof Let
![]() $G=E_7$
. Then its extended Dynkin diagram is given as follows.
$G=E_7$
. Then its extended Dynkin diagram is given as follows.

Then the facets of
![]() $\Delta _5(0)$
are
$\Delta _5(0)$
are
So we have the following acyclic partial matching.

Note that all faces of
![]() $\Delta _5(0)$
but the vertex 1 appear in the acyclic partial matching above. Thus, by the fundamental theorem of discrete Morse theory,
$\Delta _5(0)$
but the vertex 1 appear in the acyclic partial matching above. Thus, by the fundamental theorem of discrete Morse theory,
![]() $\Delta _5(0)$
collapses onto the vertex 1, implying
$\Delta _5(0)$
collapses onto the vertex 1, implying
![]() $\Delta _5(0)$
is contractible. By Lemma 7.2, the facets of
$\Delta _5(0)$
is contractible. By Lemma 7.2, the facets of
![]() $\Delta _7(0)$
are 18 and 78. Then
$\Delta _7(0)$
are 18 and 78. Then
![]() $\Delta _7(0)$
is a path graph of length 2, implying it is contractible.
$\Delta _7(0)$
is a path graph of length 2, implying it is contractible.
Since
![]() $|W(E_8)|=2^{14}\cdot 3^5\cdot 5^2\cdot 7$
, we only need to consider
$|W(E_8)|=2^{14}\cdot 3^5\cdot 5^2\cdot 7$
, we only need to consider
![]() $\Delta _7(0)$
for
$\Delta _7(0)$
for
![]() $(G,p)=(E_8,7)$
.
$(G,p)=(E_8,7)$
.
Proposition 8.4 For
![]() $G=E_8$
,
$G=E_8$
,
![]() $\Delta _7(0)$
is contractible.
$\Delta _7(0)$
is contractible.
Proof The extended Dynkin diagram of
![]() $E_8$
is given as below.
$E_8$
is given as below.

Then, by Lemma 7.2,
![]() $\Delta _7(0)$
is the following two-dimensional simplicial complex.
$\Delta _7(0)$
is the following two-dimensional simplicial complex.

Thus
![]() $\Delta _7(0)$
is contractible.
$\Delta _7(0)$
is contractible.