We provide a complete classification, up to order-isomorphism, of all possible Wadge hierarchies on zero-dimensional Polish spaces using (essentially) countable ordinals as complete invariants. We also observe that although our assignment of invariants is very simple and there are only 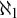$ \aleph _1 $-many equivalence classes, the above classification problem is quite complex from the descriptive set-theoretic point of view: in particular, there is no Borel procedure to determine whether two zero-dimensional Polish spaces have isomorphic Wadge hierarchies. All results are based on a complete and explicit description of the Wadge hierarchy on an arbitrary zero-dimensional Polish space, depending on its topological properties.

We prove that the Wadge order on the Borel subsets of the Scott domain is not a well-quasi-order, and that this feature even occurs among the sets of Borel rank at most 2. For this purpose, a specific class of countable 2-colored posets $\mathbb{P}_{emb} $ equipped with the order induced by homomorphisms is embedded into the Wadge order on the $\Delta _2^0 $-degrees of the Scott domain. We then show that $\mathbb{P}_{emb} $ admits both infinite strictly decreasing chains and infinite antichains with respect to this notion of comparison, which therefore transfers to the Wadge order on the $\Delta _2^0 $-degrees of the Scott domain.

The Axiom of Projective Determinacy implies the existence of a universal set for every n ≥ 1. Assuming there exists a universal set. In ZFC there is a universal set for every α.