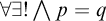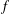Refine search
Actions for selected content:
3 results
ALGEBRAIC EXPANSIONS OF LOGICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 22 June 2022, pp. 74-92
- Print publication:
- March 2023
-
- Article
- Export citation
GAPS IN TAYLOR SERIES OF ALGEBRAIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 412-418
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Correct rounding of algebraic functions
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 41 / Issue 1 / January 2007
- Published online by Cambridge University Press:
- 24 April 2007, pp. 71-83
- Print publication:
- January 2007
-
- Article
- Export citation