No CrossRef data available.
Article contents
ALGEBRAIC EXPANSIONS OF LOGICS
Published online by Cambridge University Press: 22 June 2022
Abstract
An algebraically expandable (AE) class is a class of algebraic structures axiomatizable by sentences of the form 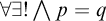 $\forall \exists ! \mathop{\boldsymbol {\bigwedge }}\limits p = q$. For a logic L algebraized by a quasivariety
$\forall \exists ! \mathop{\boldsymbol {\bigwedge }}\limits p = q$. For a logic L algebraized by a quasivariety  $\mathcal {Q}$ we show that the AE-subclasses of
$\mathcal {Q}$ we show that the AE-subclasses of  $\mathcal {Q}$ correspond to certain natural expansions of L, which we call algebraic expansions. These turn out to be a special case of the expansions by implicit connectives studied by X. Caicedo. We proceed to characterize all the AE-subclasses of abelian
$\mathcal {Q}$ correspond to certain natural expansions of L, which we call algebraic expansions. These turn out to be a special case of the expansions by implicit connectives studied by X. Caicedo. We proceed to characterize all the AE-subclasses of abelian 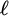 $\ell $-groups and perfect MV-algebras, thus fully describing the algebraic expansions of their associated logics.
$\ell $-groups and perfect MV-algebras, thus fully describing the algebraic expansions of their associated logics.
Keywords
MSC classification
Primary:
03G27: Abstract algebraic logic
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
Belluce, L. P., Di Nola, A., and Gerla, B., Perfect MV-algebras and their logic
.
Applied Categorical Structures
, vol. 15 (2007), nos. 1–2, pp. 135–151.CrossRefGoogle Scholar
Blok, W. J. and Ferreirim, I. M. A., On the structure of hoops
.
Algebra Universalis
, vol. 43 (2000), nos. 2–3, pp. 233–257.CrossRefGoogle Scholar
Burris, S. and Sankappanavar, H.,
A Course in Universal Algebra
, Graduate Texts in Mathematics, vol. 78, Springer, New York, 1981.CrossRefGoogle Scholar
Caicedo, X., Implicit connectives of algebraizable logics
.
Studia Logica
, vol. 78 (2004), nos. 1–2, pp. 155–170.Google Scholar
Caicedo, X., Implicit operations in MV-algebras and the connectives of Łukasiewicz logic
,
Algebraic and Proof-Theoretic Aspects of Non-Classical Logics
, Lecture Notes in Computer Science, vol. 4460, Springer, Berlin–Heidelberg, 2007.CrossRefGoogle Scholar
Caicedo, X. and Cignoli, R., An algebraic approach to intuitionistic connectives, this Journal, vol. 66 (2001), no. 4, pp. 1620–1636.Google Scholar
Campercholi, M., Algebraically expandable classes of Heyting algebras, preprint, 2010.CrossRefGoogle Scholar
Campercholi, M., Algebraically expandable classes of implication algebras
.
International Journal of Algebra and Computation
, vol. 20 (2010), no. 5, pp. 605–617.Google Scholar
Campercholi, M. and Vaggione, D., Algebraically expandable classes
.
Algebra Universalis
, vol. 61 (2009), no. 2, pp. 151–186.CrossRefGoogle Scholar
Campercholi, M. and Vaggione, D., Algebraic functions
.
Studia Logica
, vol. 98 (2011), nos. 1–2, pp. 285–306.CrossRefGoogle Scholar
Cignoli, R. L. O., D’Ottaviano, I. M. L., and Mundici, D.,
Algebraic Foundations of Many-Valued Reasoning
, Trends in Logic—Studia Logica Library, vol. 7, Kluwer Academic, Dordrecht, 2000.CrossRefGoogle Scholar
Di Nola, A. and Lettieri, A., Perfect MV-algebras are categorically equivalent to abelian
 $l$
-groups
.
Studia Logica
, vol. 53 (1994), no. 3, pp. 417–432.CrossRefGoogle Scholar
$l$
-groups
.
Studia Logica
, vol. 53 (1994), no. 3, pp. 417–432.CrossRefGoogle Scholar
Ferreirim, I. M. A.,
On Varieties and Quasivarieties of Hoops and Their Reducts
, ProQuest LLC, Ann Arbor, 1992, Ph.D. thesis, University of Illinois at Chicago.Google Scholar
Font, J. M.,
Abstract Algebraic Logic: An Introductory Textbook
, Studies in Logic: Mathematical Logic and Foundations, vol. 60, College Publications, London, 2016.Google Scholar
Galli, A., Lewin, R. A., and Sagastume, M., The logic of equilibrium and abelian lattice ordered groups
.
Archive for Mathematical Logic
, vol. 43 (2004), no. 2, pp. 141–158.CrossRefGoogle Scholar
Glass, A. M. W.,
Partially Ordered Groups
, Series in Algebra, vol. 7, World Scientific, River Edge, 1999.CrossRefGoogle Scholar
Gramaglia, H. and Vaggione, D., Birkhoff-like sheaf representation for varieties of lattice expansions
.
Studia Logica
, vol. 56 (1996), nos. 1–2, pp. 111–131. Special issue on Priestley duality.Google Scholar
Hodges, W.,
Model Theory
, Encyclopedia of Mathematics and Its Applications, vol. 42, Cambridge University Press, Cambridge, 1993.CrossRefGoogle Scholar
Jónsson, B., Algebras whose congruence lattices are distributive
.
Mathematica Scandinavica
, vol. 21 (1968), pp. 110–121.CrossRefGoogle Scholar
Metcalfe, G., Olivetti, N., and Gabbay, D., Sequent and hypersequent calculi for abelian and Łukasiewicz logics
.
ACM Transactions on Computational Logic
, vol. 6 (2005), no. 3, pp. 578–613.CrossRefGoogle Scholar
Mundici, D., Interpretation of AF
 ${C}^{\ast }$
-algebras in Łukasiewicz sentential calculus
.
Journal of Functional Analysis
, vol. 65 (1986), no. 1, pp. 15–63.CrossRefGoogle Scholar
${C}^{\ast }$
-algebras in Łukasiewicz sentential calculus
.
Journal of Functional Analysis
, vol. 65 (1986), no. 1, pp. 15–63.CrossRefGoogle Scholar
Mundici, D., Mapping abelian
 $l$
-groups with strong unit one–one into MV algebras
.
Journal of Algebra
, vol. 98 (1986), no. 1, pp. 76–81.CrossRefGoogle Scholar
$l$
-groups with strong unit one–one into MV algebras
.
Journal of Algebra
, vol. 98 (1986), no. 1, pp. 76–81.CrossRefGoogle Scholar
Volger, H., Preservation theorems for limits of structures and global sections of sheaves of structures
.
Mathematische Zeitschrift
, vol. 166 (1979), no. 1, pp. 27–54.CrossRefGoogle Scholar
Weinberg, E. C., Free lattice-ordered abelian groups. II
.
Mathematische Annalen
, vol. 159 (1965), pp. 217–222.CrossRefGoogle Scholar


