1 results
On regular algebraic hypersurfaces with non-zero constant mean curvature in Euclidean spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 06 September 2021, pp. 1081-1088
- Print publication:
- August 2022
-
- Article
- Export citation
-
We prove that there are no regular algebraic hypersurfaces with non-zero constant mean curvature in the Euclidean space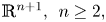
$\mathbb {R}^{n+1},\,\;n\geq 2,$ defined by polynomials of odd degree. Also we prove that the hyperspheres and the round cylinders are the only regular algebraic hypersurfaces with non-zero constant mean curvature in 
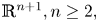$\mathbb {R}^{n+1}, n\geq 2,$ defined by polynomials of degree less than or equal to three. These results give partial answers to a question raised by Barbosa and do Carmo.
