Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T08:16:23.599Z Has data issue: false hasContentIssue false
  • English
  • Français

On regular algebraic hypersurfaces with non-zero constant mean curvature in Euclidean spaces

Part of: Global differential geometry Classical differential geometry

Published online by Cambridge University Press:  06 September 2021

Alexandre Paiva Barreto ,
Francisco Fontenele  and
Luiz Hartmann Open the ORCID record for Luiz Hartmann [Opens in a new window]
Alexandre Paiva Barreto
Affiliation:
Departamento de Matemática, Universidade Federal de São Carlos, São Carlos, SP, Brazil (alexandre@dm.ufscar.br, alexandre.paiva@ufscar.br)
Francisco Fontenele
Affiliation:
Departamento de Geometria, Universidade Federal Fluminense, Niterói, RJ, Brazil (fontenele@mat.uff.br)
Luiz Hartmann
Affiliation:
Departamento de Matemática, Universidade Federal de São Carlos, São Carlos, SP, Brazil (luizhartmann@ufscar.br, hartmann@dm.ufscar.br)
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that there are no regular algebraic hypersurfaces with non-zero constant mean curvature in the Euclidean space 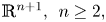$\mathbb {R}^{n+1},\,\;n\geq 2,$ defined by polynomials of odd degree. Also we prove that the hyperspheres and the round cylinders are the only regular algebraic hypersurfaces with non-zero constant mean curvature in 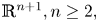$\mathbb {R}^{n+1}, n\geq 2,$ defined by polynomials of degree less than or equal to three. These results give partial answers to a question raised by Barbosa and do Carmo.

Keywords

Constant mean curvaturealgebraic hypersurface

MSC classification

Primary: 53C42: Immersions (minimal, prescribed curvature, tight, etc.)
Secondary: 53A10: Minimal surfaces, surfaces with prescribed mean curvature
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 4 , August 2022 , pp. 1081 - 1088
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aleksandrov, A. D.. Uniqueness theorems for surfaces in the large. Vestnik Leningrad Univ. Math. 13 (1958), 5–8.Google Scholar
Barbosa, J. L., Birbrair, L., do Carmo, M. and Fernandes, A.. Globally subanalytic CMC surfaces in $\mathbb {R}^{3}$. Electron. Res. Announc. Math. Sci. 21 (2014), 186–192.Google Scholar
Barbosa, J. L. and do Carmo, M.. On regular algebraic surfaces of $\mathbb {R}^{3}$ with constant mean curvature. J. Differential Geom. 102 (2016), 173–178.CrossRefGoogle Scholar
López, R.. Surfaces with constant mean curvature in Euclidean space. Int. Electron. J. Geom. 3 (2010), 67–101.Google Scholar
Nitsche, J. C. C.. Lectures on Minimal Surfaces, Vol. 1 (Cambridge: Cambridge University Press, 1989), Introduction, fundamentals, geometry and basic boundary value problems. Translated from the German by Jerry M. Feinberg, With a German foreword.Google Scholar
Odehnal, B.. On algebraic minimal surfaces. KoG 20 (2016), 61–78.Google Scholar
Perdomo, O.. Algebraic constant mean curvature surfaces in Euclidean space. Houston J. Math. 39 (2013), 127–136.Google Scholar
Perdomo, O. and Tkachev, V. G.. Algebraic CMC hypersurfaces of order 3 in Euclidean spaces. J. Geom. 110 (2019), 5–10.CrossRefGoogle Scholar
Sampaio, J. E.. Globally subanalytic CMC surfaces in $\mathbb {R}^{3}$ with singularities. Proc. Roy. Soc. Edinburgh Sect. A 151 (2021), 407–424.CrossRefGoogle Scholar
Small, A.. Algebraic minimal surfaces in $\mathbb {R}^{4}$. Math. Scand. 94 (2004), 109–124.CrossRefGoogle Scholar
Small, A.. On algebraic minimal surfaces in $\mathbb {R}^{3}$ deriving from charge 2 monopole spectral curves. Internat. J. Math. 16 (2005), 173–180.CrossRefGoogle Scholar
Tkachev, V.. Minimal cubic cones via Clifford algebras. Complex Anal. Oper. Theory 4 (2010), 685–700.CrossRefGoogle Scholar