Let $\dot{x}=f(x,u)$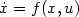 be a general control system; the existence of a smooth control-Lyapunov function does not imply the existence of a continuous stabilizing feedback. However, we show that it allows us to design a stabilizing feedback in the Krasovskii (or Filippov) sense. Moreover, we recall a definition of a control-Lyapunov function in the case of a nonsmooth function; it is based on Clarke's generalized gradient. Finally, with an inedite proof we prove that the existence of this type of control-Lyapunov function is equivalent to the existence of a classical control-Lyapunov function. This property leads to a generalization of a result on the systems with integrator.