Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T22:21:59.206Z Has data issue: false hasContentIssue false
  • English
  • Français

On the existence of nonsmooth control-Lyapunov functions in the sense of generalized gradients

Published online by Cambridge University Press:  15 August 2002

Ludovic Rifford
Ludovic Rifford*
Affiliation:
Institut Girard Desargues, Université Claude Bernard Lyon I, 69622 Villeurbanne, France; rifford@desargues.univ-lyon1.fr.
Get access

Abstract

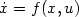Let $\dot{x}=f(x,u)$ be a general control system; the existence of a smooth control-Lyapunov function does not imply the existence of a continuous stabilizing feedback. However, we show that it allows us to design a stabilizing feedback in the Krasovskii (or Filippov) sense. Moreover, we recall a definition of a control-Lyapunov function in the case of a nonsmooth function; it is based on Clarke's generalized gradient. Finally, with an inedite proof we prove that the existence of this type of control-Lyapunov function is equivalent to the existence of a classical control-Lyapunov function. This property leads to a generalization of a result on the systems with integrator.

Keywords

Asymptotic stabilizabilityconverse Lyapunov theoremnonsmooth analysisdifferential inclusionand Krasovskii solutionsfeedback.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 6 , 2001 , pp. 593 - 611
Copyright
© EDP Sciences, SMAI, 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Artstein, Z., Stabilization with relaxed controls. Nonlinear Anal. 7 (1983) 1163-1173. CrossRef
J.-P. Aubin, Viability theory. Birkhäuser Boston Inc., Boston, MA (1991).
J.P. Aubin and A. Cellina, Differential Inclusions. Springer-Verlag (1984).
J.P. Aubin and H. Frankowska, Set-valued analysis. Birkhäuser (1990).
Byrnes, C.I. and Isidori, A., New results and examples in nonlinear feedback stabilization. Systems Control Lett. 12 (1989) 437-442. CrossRef
Clarke, F.H., Ledyaev, Yu.S., Rifford, L. and Stern, R.J., Feedback stabilization and Lyapunov functions. SIAM J. Control Optim. 39 (2000) 25-48. CrossRef
F.H. Clarke, Optimization and Nonsmooth Analysis. Wiley-Interscience, New York (1983). Republished as Classics Appl. Math. 5 (1990).
Clarke, F.H., Ledyaev, Yu.S. and Stern, R.J., Asymptotic stability and smooth Lyapunov functions. J. Differential Equations 149 (1998) 69-114. CrossRef
F.H. Clarke, Yu.S. Ledyaev, R.J. Stern and P.R. Wolenski, Nonsmooth Analysis and Control Theory. Springer-Verlag, New York, Grad. Texts in Math. 178 (1998).
J.-M. Coron, On the stabilization of some nonlinear control systems: Results, tools, and applications, in Nonlinear analysis, differential equations and control (Montreal, QC, 1998). Kluwer Acad. Publ., Dordrecht (1999) 307-367.
J.-M. Coron, Some open problems in control theory, in Differential geometry and control (Boulder, CO, 1997). Providence, RI, Amer. Math. Soc. (1999) 149-162.
Coron, J.-M. and Rosier, L., A relation between continuous time-varying and discontinuous feedback stabilization. J. Math. Systems Estim. Control 4 (1994) 67-84.
K. Deimling, Multivalued Differential Equations. de Gruyter, Berlin (1992).
A.F. Filippov, Differential Equations with Discontinuous Righthand Sides. Kluwer Academic Publishers (1988).
R. Freeman and P.V. Kokotovic, Robust Nonlinear Control Design. State-Space and Lyapunov Techniques. Birkhäuser (1996).
R.A. Freeman and P.V. Kokotovic, Backstepping design with nonsmooth nonlinearities, in Proc. of the IFAC Nonlinear Control Systems design symposium. Tahoe City, California (1995).
Hájek, O., Discontinuous differential equations. I, II. J. Differential Equations 32 (1979) 149-170, 171-185. CrossRef
Hiriart-Urruty, J.-B. and Imbert, C., Les fonctions d'appui de la jacobienne généralisée de Clarke et de son enveloppe plénière. C. R. Acad. Sci. Paris Sér. I Math. 326 (1998) 1275-1278. CrossRef
N.N. Krasovskiĭ, Stability of motion. Applications of Lyapunov's second method to differential systems and equations with delay. Stanford University Press, Stanford, California (1963). Translated by J.L. Brenner.
Kurzweil, J., On the inversion of Lyapunov's second theorem on stability of motion. Amer. Math. Soc. Transl. Ser. 2 24 (1956) 19-77.
Yu.S. Ledyaev, E.D. Sontag, A Lyapunov characterization of robust stabilization. Nonlinear Anal. 37 (1999) 813-840. CrossRef
Lin, Y., Sontag, E.D. and Wang, Y., A smooth converse Lyapunov theorem for robust stability. SIAM J. Control Optim. 34 (1996) 124-160. CrossRef
Massera, J.L., Contributions to stability theory. Ann. of Math. (2) 64 (1956) 182-206. CrossRef
Michael, E., Continuous selections. I. Ann. of Math. (2) 63 (1956) 361-382. CrossRef
L. Praly and A.R. Teel, On assigning the derivative of a disturbance attenuation clf, in Proc. of the 37th IEEE conference on decision and control. Tampa, Florida (1998).
Rifford, L., Existence of Lipschitz and semiconcave control-Lyapunov functions. SIAM J. Control Optim. 39 (2000) 1043-1064. CrossRef
L. Rosier, Étude de quelques problèmes de stabilisation, Ph.D. Thesis. ENS de Cachan (1993).
Sontag, E.D., A ``universal'' construction of Artstein's theorem on nonlinear stabilization. Systems Control Lett. 13 (1989) 117-123. CrossRef
E.D. Sontag, Mathematical Control Theory. Springer-Verlag, New York, Texts Appl. Math. 6 (1990) (Second Edition, 1998).
E.D. Sontag, Stability and stabilization: Discontinuities and the effect of disturbances, in Nonlinear analysis, differential equations and control (Montreal, QC, 1998). Kluwer Acad. Publ., Dordrecht (1999) 551-598.
Teel, A.R. and Praly, L., A smooth Lyapunov function from a class- $\mathcal{K}\mathcal{L}$ estimate involving two positive semidefinite functions. ESAIM: COCV 5 (2000) 313-367. CrossRef
Tsinias, J., Lyapunov de, Ascription of stability in control systems. Nonlinear Anal. 13 (1989) 3-74. CrossRef
Tsinias, J., Sufficient Lyapunov-like conditions for stabilization. Math. Control Signals Systems 2 (1989) 343-357. CrossRef
Tsinias, J., A local stabilization theorem for interconnected systems. Systems Control Lett. 18 (1992) 429-434. CrossRef
Tsinias, J., An extension of Artstein's theorem on stabilization by using ordinary feedback integrators. Systems Control Lett. 20 (1993) 141-148. CrossRef