1 results
A Remark on the Moser-Aubin Inequality for Axially Symmetric Functions on the Sphere
-
- Journal:
- Canadian Mathematical Bulletin / Volume 42 / Issue 4 / 01 December 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 478-485
- Print publication:
- 01 December 1999
-
- Article
-
- You have access
- Export citation
-
Let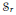
${{\mathcal{S}}_{r}}$ be the collection of all axially symmetric functions 
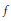$f$ in the Sobolev space 
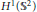${{H}^{1}}\left( {{\mathbb{S}}^{2}} \right)$ such that 
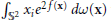$\int_{{{\mathbb{S}}^{2}}}{{{x}_{i}}{{e}^{2f\left( x \right)}}\,dw\left( \text{x} \right)}$ vanishes for 
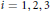$i\,=\,1,\,2,\,3$. We prove that
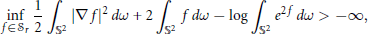$$\underset{f\in {{\mathcal{S}}_{r}}}{\mathop \inf }\,\frac{1}{2}\int_{{{\mathbb{S}}^{2}}}{{{\left| \nabla f \right|}^{2}}\,dw\,+\,2\,\int_{{{\mathbb{S}}^{2}}}{f\,dw\,-\,\log \,\int_{{{\mathbb{S}}^{2}}}{{{e}^{2f}}\,dw\,>\,-\infty ,}}}$$and that this infimum is attained. This complements recent work of Feldman, Froese, Ghoussoub and Gui on a conjecture of Chang and Yang concerning the Moser-Aubin inequality.
