Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T05:50:38.053Z Has data issue: false hasContentIssue false
  • English
  • Français

A Remark on the Moser-Aubin Inequality for Axially Symmetric Functions on the Sphere

Published online by Cambridge University Press:  20 November 2018

Alexander R. Pruss
Alexander R. Pruss*
Affiliation:
Department of Philosophy, University of Pittsburgh Pittsburgh, Pennsylvania 15260, U.S.A., e-mail: pruss+@pitt.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 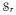${{\mathcal{S}}_{r}}$ be the collection of all axially symmetric functions 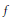$f$ in the Sobolev space 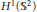${{H}^{1}}\left( {{\mathbb{S}}^{2}} \right)$ such that $\int_{{{\mathbb{S}}^{2}}}{{{x}_{i}}{{e}^{2f\left( x \right)}}\,dw\left( \text{x} \right)}$ vanishes for 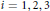$i\,=\,1,\,2,\,3$. We prove that

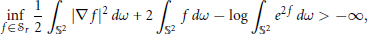$$\underset{f\in {{\mathcal{S}}_{r}}}{\mathop \inf }\,\frac{1}{2}\int_{{{\mathbb{S}}^{2}}}{{{\left| \nabla f \right|}^{2}}\,dw\,+\,2\,\int_{{{\mathbb{S}}^{2}}}{f\,dw\,-\,\log \,\int_{{{\mathbb{S}}^{2}}}{{{e}^{2f}}\,dw\,>\,-\infty ,}}}$$

and that this infimum is attained. This complements recent work of Feldman, Froese, Ghoussoub and Gui on a conjecture of Chang and Yang concerning the Moser-Aubin inequality.

Keywords

26D1558G30Moser inequalityborderline Sobolev inequalitiesaxially symmetric functions
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 4 , 01 December 1999 , pp. 478 - 485
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Aubin, Thierry, Meilleures constantes dans le th´eor`eme d’inclusion de Sobolev et un th´eor`eme de Fredholm non lin´eaire pour la transformation conforme de la courbure scalaire. J. Funct. Anal. 32 (1979), 148–174.Google Scholar
[2] Beckner, W., Moser-Trudinger inequality in higher dimensions. Duke Math. J. 64 (1991), 83–91.Google Scholar
[3] Beckner, W., Sobolev inequalities, the Poisson semigroup and analysis on the sphere Sn. Proc. Nat. Acad. Sci. U.S.A. 89 (1992), 4816–4819.Google Scholar
[4] Beckner, W., Sharp Sobolev inequalities on the sphere and the Moser-Trudinger inequality. Ann. of Math. 138 (1993), 213–242.Google Scholar
[5] Beckner, W., Geometric inequalities in Fourier analysis. Essays on Fourier Analysis in Honor of Elias M. Stein (eds. Charles Fefferman, Robert Fefferman and Stephen Wainger), Princeton Mathematical Series, 42, Princeton Univ. Press, Princeton, New Jersey, 1995.Google Scholar
[6] Chang, S.-Y. A. and Yang, P., Prescribing Gaussian curvature on S2. Acta Math. 159 (1987), 214–259.Google Scholar
[7] Chang, S.-Y. A. and Yang, P., Conformal deformations of metrics on S2. J. Differential Geom. 27 (1988), 215–259.Google Scholar
[8] Feldman, J., Froese, R., Ghoussoub, N. and Gui, C., An improved Moser-Aubin-Onofri inequality for axially symmetric functions on S2, Calculus of Variations and PDE 6 (1998), 95–104.Google Scholar
[9] Kazdan, J. and Warner, F., Curvature functions for compact 2-manifolds. Ann. ofMath. 99 (1974), 14–47.Google Scholar
[10] Kazdan, J. and Warner, F., Scalar curvature and conformal deformation of Riemannian structure. J. Differential Geom. 10 (1975), 113–134.Google Scholar
[11] Moser, J., A sharp form of an inequality by N. Trudinger. Indiana Univ. Math. J. 20 (1971), 1077–1092.Google Scholar
[12] Onofri, E., On the positiivity of the effective action in a theorem on random surfaces. Comm. Math. Phys. 86 (1982), 321–326.Google Scholar
[13] Osgood, B., Phillips, R. and Sarnak, P., Extremals of determinants of Laplacians. J. Funct. Anal. 80 (1988), 148–211.Google Scholar