We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The aim of this paper is twofold. The first aim is to describe the entire solutions of the partial differential equation (PDE)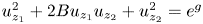 
$u_{z_1}^2+2Bu_{z_1}u_{z_2}+u_{z_2}^2=e^g$, where B is a constant and g is a polynomial or an entire function in 
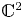$\mathbb {C}^2$. The second aim is to consider the entire solutions of another PDE, which is a generalization of the well-known PDE of tubular surfaces.
