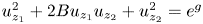Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lü, Feng
and
Bi, Wenqi
2022.
On entire solutions of certain partial differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 516,
Issue. 1,
p.
126476.
Chen, Wei
and
Han, Qi
2022.
On entire solutions to eikonal-type equations.
Journal of Mathematical Analysis and Applications,
Vol. 506,
Issue. 1,
p.
124704.
Xu, Hongyan
Xu, Ling
and
Srivastava, Hari Mohan
2022.
The Exact Solutions for Several Partial Differential-Difference Equations with Constant Coefficients.
Mathematics,
Vol. 10,
Issue. 19,
p.
3596.
Xu, Hong Yan
Xu, Yi Hui
and
Liu, Xiao Lan
2023.
On solutions for several systems of complex nonlinear partial differential equations with two variables.
Analysis and Mathematical Physics,
Vol. 13,
Issue. 3,
Xu, Yi Hui
Li, Yan Fang
Liu, Xiao Lan
and
Xu, Hong Yan
2023.
Transcendental entire solutions of several complex product-type nonlinear partial differential equations in ℂ2
.
Open Mathematics,
Vol. 21,
Issue. 1,
Liu, Xiao Lan
Xu, Hong Yan
Xu, Yi Hui
and
Li, Nan
2024.
Results on solutions of several systems of the product type complex partial differential difference equations.
Demonstratio Mathematica,
Vol. 57,
Issue. 1,
Xu, Hong Yan
and
Haldar, Goutam
2024.
Entire solutions to Fermat-type difference and partial differential-difference equations in C^n.
Electronic Journal of Differential Equations,
Vol. 2024,
Issue. 01-??,
p.
26.
Tu, Jin
and
Wei, Huizhen
2024.
Form of solutions to quadratic trinomial partial differential equations with two complex variables.
Electronic Journal of Differential Equations,
Vol. 2024,
Issue. 01-??,
p.
23.
Li, Hong
Luo, Zhao Sheng
and
Xu, Hong Yan
2024.
Study on solutions of the systems of complex product-type PDEs with more general forms in ℂ2
.
Open Mathematics,
Vol. 22,
Issue. 1,
Jiao, Xin
Chen, Yu Bin
and
Xu, Hong Yan
2025.
A study of solutions for several classes of systems of complex nonlinear partial differential difference equations in ℂ2
.
Demonstratio Mathematica,
Vol. 58,
Issue. 1,
郭, 惠媛
2025.
Transcendental Entire Solutions to a Class of Complex Partial Differential Equation
Systems.
Advances in Applied Mathematics,
Vol. 14,
Issue. 07,
p.
197.
Yang, L.
Chen, W.
and
Wang, Q.
2025.
Entire solutions of the eiconal type partial differential equations in $$\mathbb{C}^2$$.
Analysis Mathematica,
Vol. 51,
Issue. 2,
p.
727.
Xu, Hong Yan
Liu, Kai
and
Xuan, Zuxing
2025.
Results on solutions of several product type nonlinear partial differential equations in C3.
Journal of Mathematical Analysis and Applications,
Vol. 543,
Issue. 1,
p.
128885.
Xu, Hong Yan
and
Srivastava, Hari Mohan
2025.
A study of transcendental entire solutions of several nonlinear partial differential equations.
Proceedings of the Edinburgh Mathematical Society,
p.
1.