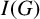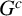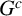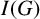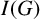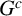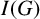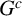We find asymptotics of the maximum size of a chordal subgraph in a binomial random graph $G(n,p)$, for $p=\mathrm{const}$ and $p=n^{-\alpha +o(1)}$.

It is well known that the edge ideal $I(G)$ of a simple graph G has linear quotients if and only if $G^c$ is chordal. We investigate when the property of having linear quotients is inherited by homological shift ideals of an edge ideal. We will see that adding a cluster to the graph $G^c$ when $I(G)$ has homological linear quotients results in a graph with the same property. In particular, $I(G)$ has homological linear quotients when $G^c$ is a block graph. We also show that adding pinnacles to trees preserves the property of having homological linear quotients for the edge ideal of their complements. Furthermore, $I(G)$ has homological linear quotients for every graph G such that $G^c$ is a $\lambda $-minimal chordal graph.

Let $X\subset \mathbb{P}^r$ be a closed scheme in projective space whose homogeneous ideal is generated by quadrics. We say that X (or its ideal IX) satisfies the condition N2,p if the syzygies of IX are linear for p steps. We show that if X satisfies N2,p then a zero-dimensional or one-dimensional intersection of X with a plane of dimension $\leq p$ is 2-regular. This extends a result of Green and Lazarsfeld. We give conditions when the syzygies of X restrict to the syzygies of the intersection. Many of our results also work for ideals generated by forms of higher degree. As applications, we bound the p for which some well-known projective varieties satisfy N2,p. Another application, carried out by us in a different paper, is a step in the classification of 2-regular reduced projective schemes. Extending a result of Fröberg, we determine which monomial ideals satisfy N2,p. We also apply Green's ‘linear syzygy theorem’ to deduce a relation between the resolutions of IX and $I_{X\cup \Gamma}$ for a scheme Γ, and apply the result to bound the number of intersection points of certain pairs of varieties such as rational normal scrolls.