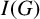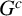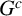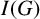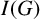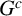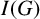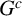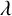1 Introduction
Let
![]() $S=K[x_1,\ldots , x_n]$
be the polynomial ring in the variables
$S=K[x_1,\ldots , x_n]$
be the polynomial ring in the variables
![]() $x_1,\ldots , x_n$
over a field K with its natural multigrading. Throughout, a monomial and its multidegree will be used interchangeably and
$x_1,\ldots , x_n$
over a field K with its natural multigrading. Throughout, a monomial and its multidegree will be used interchangeably and
![]() $S(\boldsymbol {x}^{\boldsymbol {a}})$
denotes the free S-module with one generator of multidegree
$S(\boldsymbol {x}^{\boldsymbol {a}})$
denotes the free S-module with one generator of multidegree
![]() $\boldsymbol {x}^{\boldsymbol {a}}$
. A monomial ideal
$\boldsymbol {x}^{\boldsymbol {a}}$
. A monomial ideal
![]() $I\subseteq S$
has a (unique up to isomorphism) minimal multigraded resolution
$I\subseteq S$
has a (unique up to isomorphism) minimal multigraded resolution
with
The kth homological shift ideal of I denoted by
![]() $\mathrm {HS}_k(I)$
is the ideal generated by the kth multigraded shifts of I, that is,
$\mathrm {HS}_k(I)$
is the ideal generated by the kth multigraded shifts of I, that is,
Recently, properties of monomial ideals which are inherited by their homological shift ideals have attracted attention. It is shown in [Reference Bayati1, Theorem 3.2] that if I is a matroidal ideal, then so are its homological shift ideals. It is still an open question whether a similar statement holds if one replaces matroidal by polymatroidal. However, there are some partial positive answers for some classes of polymatroidal ideals including polymatroidal ideals satisfying the strong exchange property [Reference Herzog, Moradi, Rahimbeigi and Zhu13, Corollary 3.6], Veronese-type ideals [Reference Herzog, Moradi, Rahimbeigi and Zhu13, Theorem 3.3], polymatroidal ideals generated in degree two [Reference Ficarra and Herzog7, Theorem 4.5] and for the first homological shift ideal of any polymatroidal ideal [Reference Ficarra6, Theorem 2.2]. In [Reference Bayati, Jahani and Taghipour3, Proposition 3.1], analogues of these results for the property of being equigenerated squarefree Borel are presented and in [Reference Bayati2], a quasi-additive property of homological shift ideals is studied.
Having linear quotients is another property that has received considerable attention. Following [Reference Ficarra and Herzog7], we say that a monomial ideal I has homological linear quotients when I has linear quotients and
![]() $\mathrm {HS}_k(I)$
inherits this property for every k. It is shown in [Reference Bayati, Jahani and Taghipour3, Theorem 2.4] and [Reference Bayati, Jahani and Taghipour3, Theorems 2.4 and 3.3] that principal Borel ideals as well as squarefree Borel ideals have homological linear quotients (see also [Reference Herzog, Moradi, Rahimbeigi and Zhu14]). It is shown in [Reference Herzog, Moradi, Rahimbeigi and Zhu13, Theorem 2.2] that even
$\mathrm {HS}_k(I)$
inherits this property for every k. It is shown in [Reference Bayati, Jahani and Taghipour3, Theorem 2.4] and [Reference Bayati, Jahani and Taghipour3, Theorems 2.4 and 3.3] that principal Borel ideals as well as squarefree Borel ideals have homological linear quotients (see also [Reference Herzog, Moradi, Rahimbeigi and Zhu14]). It is shown in [Reference Herzog, Moradi, Rahimbeigi and Zhu13, Theorem 2.2] that even
![]() $\mathbf {c}$
-bounded principal Borel ideals have homological linear quotients. It is also proved in [Reference Ficarra and Herzog7, Theorem 1.3] that if a monomial ideal I has linear quotients, then
$\mathbf {c}$
-bounded principal Borel ideals have homological linear quotients. It is also proved in [Reference Ficarra and Herzog7, Theorem 1.3] that if a monomial ideal I has linear quotients, then
![]() $\mathrm {HS}_1(I)$
has the same property.
$\mathrm {HS}_1(I)$
has the same property.
Regarding having homological linear quotients, we restrict our attention to edge ideals of graphs. Let G be a simple graph on n vertices and
![]() $I(G)\subseteq S$
be its edge ideal. From [Reference Fröberg, Balcerzyk, Józefiak, Krempa, Simson and Vogel10] and [Reference Herzog and Hibi12, Theorem 10.2.6],
$I(G)\subseteq S$
be its edge ideal. From [Reference Fröberg, Balcerzyk, Józefiak, Krempa, Simson and Vogel10] and [Reference Herzog and Hibi12, Theorem 10.2.6],
![]() $I(G)$
has linear quotients if and only if
$I(G)$
has linear quotients if and only if
![]() $G^c$
is a chordal graph. It is shown in [Reference Ficarra and Herzog7, Proposition 3.2] that if
$G^c$
is a chordal graph. It is shown in [Reference Ficarra and Herzog7, Proposition 3.2] that if
![]() $I(G)$
has homological linear quotients, then adding a whisker to
$I(G)$
has homological linear quotients, then adding a whisker to
![]() $G^c$
gives a graph such that the edge ideal of its complement also has homological linear quotients. As a result,
$G^c$
gives a graph such that the edge ideal of its complement also has homological linear quotients. As a result,
![]() $I(G)$
has homological linear quotients when
$I(G)$
has homological linear quotients when
![]() $G^c$
is a tree. Generalising these two results, we show in Theorem 2.6 that when
$G^c$
is a tree. Generalising these two results, we show in Theorem 2.6 that when
![]() $I(G)$
has homological linear quotients, then adding clusters to
$I(G)$
has homological linear quotients, then adding clusters to
![]() $G^c$
leads to a graph such that the edge ideal of its complement has homological linear quotients. In particular, this implies that
$G^c$
leads to a graph such that the edge ideal of its complement has homological linear quotients. In particular, this implies that
![]() $I(G)$
has homological linear quotients when
$I(G)$
has homological linear quotients when
![]() $G^c$
is a block graph (see Corollary 2.7).
$G^c$
is a block graph (see Corollary 2.7).
Next, we consider another construction of adding pinnacles which preserves the property of having linear quotients for homological shift ideals (see Section 3 for the definition). We will see in Theorem 3.1 that if
![]() $G^c$
is obtained by adding pinnacles to a tree, then
$G^c$
is obtained by adding pinnacles to a tree, then
![]() $I(G)$
has homological linear quotients. Finally, we see in Corollary 3.4 that
$I(G)$
has homological linear quotients. Finally, we see in Corollary 3.4 that
![]() $I(G)$
has homological linear quotients if
$I(G)$
has homological linear quotients if
![]() $G^c$
is a
$G^c$
is a
![]() $\lambda $
-minimal graph.
$\lambda $
-minimal graph.
2 Block graphs
Throughout,
![]() $S=K[x_1,\ldots ,x_n]$
denotes a polynomial ring over a field K with its natural multigrading. If
$S=K[x_1,\ldots ,x_n]$
denotes a polynomial ring over a field K with its natural multigrading. If
![]() $u,v\in S$
are monomials, then
$u,v\in S$
are monomials, then
![]() $u:v$
denotes the monomial
$u:v$
denotes the monomial
![]() ${u}/{\gcd (u,v)}$
. For a monomial
${u}/{\gcd (u,v)}$
. For a monomial
![]() $u\in S$
, we set
$u\in S$
, we set
![]() $\max u= \max \{k \mid x_k$
divides
$\max u= \max \{k \mid x_k$
divides
![]() $u\}$
. When
$u\}$
. When
![]() ${\ell = \max u}$
, we may sometimes write
${\ell = \max u}$
, we may sometimes write
![]() $x_\ell =\max u$
for ease of use.
$x_\ell =\max u$
for ease of use.
Let
![]() $I\subseteq S$
be a monomial ideal. We denote its minimal set of monomial generators by
$I\subseteq S$
be a monomial ideal. We denote its minimal set of monomial generators by
![]() $G(I)$
. A monomial ideal
$G(I)$
. A monomial ideal
![]() $I\subseteq S$
is said to have linear quotients if there exists an ordering
$I\subseteq S$
is said to have linear quotients if there exists an ordering
![]() $u_1,\ldots ,u_r$
of the elements of
$u_1,\ldots ,u_r$
of the elements of
![]() $G(I)$
, called an admissible order, such that for each
$G(I)$
, called an admissible order, such that for each
![]() $i=1,\ldots ,r-1$
, the colon ideal
$i=1,\ldots ,r-1$
, the colon ideal
![]() $(u_1,\ldots ,u_i):(u_{i+1})$
is generated by a subset of
$(u_1,\ldots ,u_i):(u_{i+1})$
is generated by a subset of
![]() $\{x_1,\ldots , x_n\}$
. If I has linear quotients with respect to the ordering
$\{x_1,\ldots , x_n\}$
. If I has linear quotients with respect to the ordering
![]() $u_1,\ldots ,u_r$
of
$u_1,\ldots ,u_r$
of
![]() $G(I)$
, we define
$G(I)$
, we define
Remark 2.1. Let a monomial ideal
![]() $I\subseteq S$
have linear quotients. By [Reference Herzog and Takayama15, Lemma 1.5], a minimal multigraded free resolution
$I\subseteq S$
have linear quotients. By [Reference Herzog and Takayama15, Lemma 1.5], a minimal multigraded free resolution
![]() $\mathbf {F}$
of I can be described as follows: the S-module
$\mathbf {F}$
of I can be described as follows: the S-module
![]() $F_i$
in homological degree i of
$F_i$
in homological degree i of
![]() $\mathbf {F}$
is the multigraded free S-module whose basis is formed by the monomials
$\mathbf {F}$
is the multigraded free S-module whose basis is formed by the monomials
![]() $u x_{\ell _1}\ldots x_{\ell _i}$
for which
$u x_{\ell _1}\ldots x_{\ell _i}$
for which
![]() $u\in \mathrm {G}(I)$
and
$u\in \mathrm {G}(I)$
and
![]() $x_{\ell _1},\ldots ,x_{\ell _i}$
are distinct elements of
$x_{\ell _1},\ldots ,x_{\ell _i}$
are distinct elements of
![]() $\mathrm {set}(u)$
.
$\mathrm {set}(u)$
.
Henceforth, all graphs considered in this paper are simple graphs. Let G be a graph on the vertex set
![]() $V(G)=\{x_1,\ldots ,x_n\}$
with edge set
$V(G)=\{x_1,\ldots ,x_n\}$
with edge set
![]() $E(G)$
. The ideal
$E(G)$
. The ideal
is called the edge ideal of G. The complement of G, denoted by
![]() $G^c$
, is the graph on the vertex set
$G^c$
, is the graph on the vertex set
![]() $V(G)$
whose edge set is
$V(G)$
whose edge set is
The set of all vertices adjacent to a vertex
![]() $x_i$
in G, denoted by
$x_i$
in G, denoted by
![]() $\mathrm {N}_G(x_i)$
, is called the neighbourhood of
$\mathrm {N}_G(x_i)$
, is called the neighbourhood of
![]() $x_i$
in G. The distance between vertices
$x_i$
in G. The distance between vertices
![]() $x_i$
and
$x_i$
and
![]() $x_j$
of a connected graph G, denoted by
$x_j$
of a connected graph G, denoted by ![]() , is the number of edges in the shortest path connecting them.
, is the number of edges in the shortest path connecting them.
A graph G is called a chordal graph if it has no induced cycle of length greater than three. An ordering
![]() $x_1>x_2>\cdots >x_n$
of vertices of a graph G is called a perfect elimination ordering if whenever a vertex
$x_1>x_2>\cdots >x_n$
of vertices of a graph G is called a perfect elimination ordering if whenever a vertex
![]() $x_i$
is adjacent to vertices
$x_i$
is adjacent to vertices
![]() $x_j$
and
$x_j$
and
![]() $x_k$
with
$x_k$
with
![]() ${i<j<k}$
, then
${i<j<k}$
, then
![]() $x_j$
and
$x_j$
and
![]() $x_k$
are also adjacent. Chordal graphs are characterised in [Reference Dirac5, Reference Fulkerson and Gross11] as those graphs whose vertices admit a perfect elimination ordering.
$x_k$
are also adjacent. Chordal graphs are characterised in [Reference Dirac5, Reference Fulkerson and Gross11] as those graphs whose vertices admit a perfect elimination ordering.
Remark 2.2. While it is known by [Reference Fröberg, Balcerzyk, Józefiak, Krempa, Simson and Vogel10] and [Reference Herzog and Hibi12, Theorem 10.2.6] that the edge ideal
![]() $I(G)$
of a graph G has linear quotients if and only if
$I(G)$
of a graph G has linear quotients if and only if
![]() $G^c$
is chordal, this property is not inherited by homological shift ideals. For example, consider the graph G presented in Figure 1. Here, the labelling of vertices gives a perfect elimination ordering of vertices with respect to
$G^c$
is chordal, this property is not inherited by homological shift ideals. For example, consider the graph G presented in Figure 1. Here, the labelling of vertices gives a perfect elimination ordering of vertices with respect to
![]() $x_1>\cdots >x_6$
and even more with respect to
$x_1>\cdots >x_6$
and even more with respect to
![]() $x_6>\cdots >x_1$
. One has
$x_6>\cdots >x_1$
. One has
and
which does not have linear quotients with respect to any ordering of its generators.

Figure 1 A chordal graph such that
![]() $\mathrm{HS}_2(I(G^c))$
does not have linear quotients.
$\mathrm{HS}_2(I(G^c))$
does not have linear quotients.
Let
![]() $u= x_{i_1}\cdots x_{i_m}\in S$
be a squarefree monomial with
$u= x_{i_1}\cdots x_{i_m}\in S$
be a squarefree monomial with
![]() $i_1<\cdots <i_m$
. We say that
$i_1<\cdots <i_m$
. We say that
![]() $x_{i_t}$
is a source variable of u with respect to a graph G, or shortly a source of u when the graph is clear from the context, if the following conditions hold:
$x_{i_t}$
is a source variable of u with respect to a graph G, or shortly a source of u when the graph is clear from the context, if the following conditions hold:
-
•
 $1\leq i_t< \max u$
;
$1\leq i_t< \max u$
; -
•
 $x_{i_t}$
is adjacent to
$x_{i_t}$
is adjacent to
 $x_{i_s}$
in G for
$x_{i_s}$
in G for
 $t<s\leq \max u$
.
$t<s\leq \max u$
.
Theorem 2.3 [Reference Herzog, Moradi, Rahimbeigi and Zhu13, Theorem 4.1].
Let G be a chordal graph. Suppose that
![]() $x_1> x_2 > \cdots > x_n$
is a perfect elimination ordering of
$x_1> x_2 > \cdots > x_n$
is a perfect elimination ordering of
![]() $V(G)$
. Then, for each k,
$V(G)$
. Then, for each k,
A graph G is said to be a biconnected graph if it is connected and nonseparable, that is, if we remove any of its vertices, the graph remains connected. A biconnected component is a maximal biconnected subgraph. A graph G is called a block graph if every biconnected component is a clique.
Let G be a graph and
![]() $v\in V(G)$
. We say that the graph H is obtained from G by adding a t-cluster or simply a cluster via v when we add
$v\in V(G)$
. We say that the graph H is obtained from G by adding a t-cluster or simply a cluster via v when we add
![]() $t-1$
new vertices
$t-1$
new vertices
![]() $y_1,\ldots ,y_{t-1}$
to
$y_1,\ldots ,y_{t-1}$
to
![]() $V(G)$
, and add all edges
$V(G)$
, and add all edges
![]() $\{y_iy_j \mid 1\leq i<j\leq t \}$
to
$\{y_iy_j \mid 1\leq i<j\leq t \}$
to
![]() $E(G)$
(note that we set
$E(G)$
(note that we set
![]() $v=y_t$
).
$v=y_t$
).
The first statement of the following lemma is a special case of [Reference Herzog, Moradi, Rahimbeigi and Zhu13, Proposition 1.7].
Lemma 2.4. Let
![]() $I\subset K[{\boldsymbol {x}}]=K[x_1,\ldots ,x_n]$
be a monomial ideal that has homological linear quotients and consider the ideal
$I\subset K[{\boldsymbol {x}}]=K[x_1,\ldots ,x_n]$
be a monomial ideal that has homological linear quotients and consider the ideal
![]() $\mathfrak {m}=(y_1,\ldots ,y_m)$
in
$\mathfrak {m}=(y_1,\ldots ,y_m)$
in
![]() $K[{\boldsymbol {y}}]=K[y_1,\ldots ,y_m] $
with m new variables. Then the kth homological shift ideal of
$K[{\boldsymbol {y}}]=K[y_1,\ldots ,y_m] $
with m new variables. Then the kth homological shift ideal of
![]() $\mathfrak {m} I\subseteq K[{\boldsymbol {x}},{\boldsymbol {y}}]$
is
$\mathfrak {m} I\subseteq K[{\boldsymbol {x}},{\boldsymbol {y}}]$
is
 $$ \begin{align*} \mathrm{HS}_k(\mathfrak{m} I)&= (y_1,\ldots,y_m)\mathrm{HS}_{k}(I)+(y_iy_j\mid 1\leq i<j\leq m)\mathrm{HS}_{k-1}(I) \\ &\quad + (y_iy_jy_k\mid 1\leq i<j<k \leq m)\mathrm{HS}_{k-2}(I)+ \cdots + (y_1\cdots y_m)\mathrm{HS}_{k-m+1}(I). \end{align*} $$
$$ \begin{align*} \mathrm{HS}_k(\mathfrak{m} I)&= (y_1,\ldots,y_m)\mathrm{HS}_{k}(I)+(y_iy_j\mid 1\leq i<j\leq m)\mathrm{HS}_{k-1}(I) \\ &\quad + (y_iy_jy_k\mid 1\leq i<j<k \leq m)\mathrm{HS}_{k-2}(I)+ \cdots + (y_1\cdots y_m)\mathrm{HS}_{k-m+1}(I). \end{align*} $$
Furthermore, the ideal
![]() $\mathrm {HS}_k(\mathfrak {m} I)$
has homological linear quotients for every k.
$\mathrm {HS}_k(\mathfrak {m} I)$
has homological linear quotients for every k.
Proof. Let
![]() $I=\mathrm {HS}_0(I)$
have linear quotients with respect to the ordering
$I=\mathrm {HS}_0(I)$
have linear quotients with respect to the ordering
![]() $u_1,u_2,\ldots ,u_{\ell }$
of its generators. Then
$u_1,u_2,\ldots ,u_{\ell }$
of its generators. Then
![]() $\mathfrak {m} I$
has simply linear quotients with respect to the order:
$\mathfrak {m} I$
has simply linear quotients with respect to the order:
With this ordering of generators,
where
![]() $\mathrm {set}(u_i) = \{x_j \mid x_j \in (u_1,\ldots ,u_{i-1}) : (u_i)\}$
. Using Remark 2.1 to construct
$\mathrm {set}(u_i) = \{x_j \mid x_j \in (u_1,\ldots ,u_{i-1}) : (u_i)\}$
. Using Remark 2.1 to construct
![]() $\mathrm {HS}_k(\mathfrak {m} I)$
gives the conclusions in Table 1.
$\mathrm {HS}_k(\mathfrak {m} I)$
gives the conclusions in Table 1.
Table 1 Conclusions for
![]() $\mathrm {HS}_k(I)$
in Lemma 2.4.
$\mathrm {HS}_k(I)$
in Lemma 2.4.

The sum of the ideals in the left column of Table 1 gives
 $$ \begin{align*} \mathrm{HS}_k(\mathfrak{m} I)&= (y_1,\ldots,y_m)\mathrm{HS}_{k}(I)+(y_iy_j\mid 1\leq i<j\leq m)\mathrm{HS}_{k-1}(I) \\ &\quad + (y_iy_jy_k\mid 1\leq i<j<k \leq m)\mathrm{HS}_{k-2}(I)+ \cdots \\ &\quad + (y_1\cdots y_m)\mathrm{HS}_{k-m+1}(I). \end{align*} $$
$$ \begin{align*} \mathrm{HS}_k(\mathfrak{m} I)&= (y_1,\ldots,y_m)\mathrm{HS}_{k}(I)+(y_iy_j\mid 1\leq i<j\leq m)\mathrm{HS}_{k-1}(I) \\ &\quad + (y_iy_jy_k\mid 1\leq i<j<k \leq m)\mathrm{HS}_{k-2}(I)+ \cdots \\ &\quad + (y_1\cdots y_m)\mathrm{HS}_{k-m+1}(I). \end{align*} $$
Next we show that
![]() $\mathrm {HS}_k(\mathfrak {m} I)$
has linear quotients for every k. Notice that each
$\mathrm {HS}_k(\mathfrak {m} I)$
has linear quotients for every k. Notice that each
![]() $\mathrm {HS}_\ell (I)$
has linear quotients by assumption. For each
$\mathrm {HS}_\ell (I)$
has linear quotients by assumption. For each
![]() $\ell $
, we fix an admissible ordering on the minimal set of monomial generators of
$\ell $
, we fix an admissible ordering on the minimal set of monomial generators of
![]() $\mathrm {HS}_\ell (I)$
, and set
$\mathrm {HS}_\ell (I)$
, and set
![]() $u>_\ell v$
for each u and v in
$u>_\ell v$
for each u and v in
![]() $G(\mathrm {HS}_\ell (I))$
if u comes before v in the fixed admissible ordering. Next we show that
$G(\mathrm {HS}_\ell (I))$
if u comes before v in the fixed admissible ordering. Next we show that
![]() $\mathrm {HS}_k(\mathfrak {m} I)$
has linear quotients with the following ordering of monomial generators of
$\mathrm {HS}_k(\mathfrak {m} I)$
has linear quotients with the following ordering of monomial generators of
![]() $\mathrm {HS}_k(\mathfrak {m} I)$
: the monomial
$\mathrm {HS}_k(\mathfrak {m} I)$
: the monomial
![]() $y_{i_1}\cdots y_{i_t}u$
with
$y_{i_1}\cdots y_{i_t}u$
with
![]() $u\in \mathrm {HS}_{k-t+1}(I)$
comes before
$u\in \mathrm {HS}_{k-t+1}(I)$
comes before
![]() $y_{j_1}\cdots y_{j_s}v$
with
$y_{j_1}\cdots y_{j_s}v$
with
![]() $v\in \mathrm {HS}_{k-s+1}(I)$
if either
$v\in \mathrm {HS}_{k-s+1}(I)$
if either
![]() $y_{i_1}\cdots y_{i_t}>_{\mathrm { glex}}y_{j_1}\cdots y_{j_s}$
or if
$y_{i_1}\cdots y_{i_t}>_{\mathrm { glex}}y_{j_1}\cdots y_{j_s}$
or if
![]() $y_{i_1}\cdots y_{i_t}=y_{j_1}\cdots y_{j_s}$
and
$y_{i_1}\cdots y_{i_t}=y_{j_1}\cdots y_{j_s}$
and
![]() $u>_{k-t+1}v$
. Here
$u>_{k-t+1}v$
. Here
![]() $>_{\mathrm {glex}}$
denotes the graded lexicographic order on
$>_{\mathrm {glex}}$
denotes the graded lexicographic order on
![]() $K[{\boldsymbol {y}}]$
induced by
$K[{\boldsymbol {y}}]$
induced by
![]() $y_1>\cdots >y_m$
. To see why this is an admissible ordering for
$y_1>\cdots >y_m$
. To see why this is an admissible ordering for
![]() $\mathrm {HS}_k(\mathfrak {m} I)$
, consider the colon
$\mathrm {HS}_k(\mathfrak {m} I)$
, consider the colon
of elements of the minimal set of monomial generators of
![]() $\mathrm {HS}_k(\mathfrak {m} I)$
in which
$\mathrm {HS}_k(\mathfrak {m} I)$
in which
![]() $y_{i_1}\cdots y_{i_t}u$
comes before
$y_{i_1}\cdots y_{i_t}u$
comes before
![]() $y_{j_1}\cdots y_{j_s}v$
in the ordering just described. Suppose that
$y_{j_1}\cdots y_{j_s}v$
in the ordering just described. Suppose that ![]() . We show that there exists
. We show that there exists
![]() $y_{\ell _1}\cdots y_{\ell _s}\tilde {v}$
in the set of generators which appears before
$y_{\ell _1}\cdots y_{\ell _s}\tilde {v}$
in the set of generators which appears before
![]() $y_{j_1}\cdots y_{j_s}v$
and
$y_{j_1}\cdots y_{j_s}v$
and
is a degree one monomial which divides w. We consider two cases.
Case 1. Assume that
![]() $y_{i_1}\cdots y_{i_t}>_{\mathrm {glex}}y_{j_1}\cdots y_{j_s}$
. By Remark 2.1, the element v in the minimal set of monomial generators of
$y_{i_1}\cdots y_{i_t}>_{\mathrm {glex}}y_{j_1}\cdots y_{j_s}$
. By Remark 2.1, the element v in the minimal set of monomial generators of
![]() $\mathrm {HS}_{k-s+1}(I)$
is a product of an element
$\mathrm {HS}_{k-s+1}(I)$
is a product of an element
![]() $\hat {v}$
in the minimal set of monomial generators of I and
$\hat {v}$
in the minimal set of monomial generators of I and
![]() $k-s+1$
pairwise distinct elements of
$k-s+1$
pairwise distinct elements of
![]() $\mathrm {set}(\hat {v})$
. If
$\mathrm {set}(\hat {v})$
. If
![]() $t>s$
, then
$t>s$
, then
![]() $k-s+1>k-t+1\geq 0$
. Thus,
$k-s+1>k-t+1\geq 0$
. Thus,
![]() $k-s+1\neq 0$
. In particular, there exists
$k-s+1\neq 0$
. In particular, there exists
![]() $x_p$
in the subset of
$x_p$
in the subset of
![]() $\mathrm {set}(\hat {v})$
that divides
$\mathrm {set}(\hat {v})$
that divides
![]() $v/\hat {v}$
. Since
$v/\hat {v}$
. Since
![]() $y_{i_r}$
divides
$y_{i_r}$
divides
![]() $y_{i_1}\cdots y_{i_t}: y_{j_1}\cdots y_{j_s}$
, it follows that
$y_{i_1}\cdots y_{i_t}: y_{j_1}\cdots y_{j_s}$
, it follows that
has the desired properties, that is, it comes before
![]() $y_{j_1}\cdots y_{j_s}v$
and its colon with respect to
$y_{j_1}\cdots y_{j_s}v$
and its colon with respect to
![]() $y_{j_1}\cdots y_{j_s}v$
is
$y_{j_1}\cdots y_{j_s}v$
is
![]() $y_{i_r}$
.
$y_{i_r}$
.
Otherwise,
![]() $t=s$
. Suppose that
$t=s$
. Suppose that
![]() $y_{i_1}\cdots y_{i_s}:y_{j_1}\cdots y_{j_s}=y_{\ell _1}\cdots y_{\ell _p}$
with
$y_{i_1}\cdots y_{i_s}:y_{j_1}\cdots y_{j_s}=y_{\ell _1}\cdots y_{\ell _p}$
with
![]() $\ell _1<\cdots <\ell _p$
. Then
$\ell _1<\cdots <\ell _p$
. Then
where
![]() $j_s=\max (y_{j_1}\ldots y_{j_s})$
has the desired properties.
$j_s=\max (y_{j_1}\ldots y_{j_s})$
has the desired properties.
Case 2. Now assume that
![]() $y_{i_1}\cdots y_{i_t}=y_{j_1}\cdots y_{j_s}$
and
$y_{i_1}\cdots y_{i_t}=y_{j_1}\cdots y_{j_s}$
and
![]() $u>_{k-s+1}v$
. Since
$u>_{k-s+1}v$
. Since
![]() $\mathrm {HS}_{k-s+1}$
has linear quotients with respect to the ordering given by
$\mathrm {HS}_{k-s+1}$
has linear quotients with respect to the ordering given by
![]() $>_{k-s+1}$
, there exists
$>_{k-s+1}$
, there exists
![]() $\tilde {v}$
in the minimal set of monomial generators of
$\tilde {v}$
in the minimal set of monomial generators of
![]() $\mathrm {HS}_{k-s+1}(I)$
such that
$\mathrm {HS}_{k-s+1}(I)$
such that
![]() $\tilde {v}>_{k-s+1}v$
and
$\tilde {v}>_{k-s+1}v$
and
![]() $\tilde {v}: v=x_p$
for some p with
$\tilde {v}: v=x_p$
for some p with
![]() $x_p\mid u:v$
. Hence,
$x_p\mid u:v$
. Hence,
![]() $y_{j_1}\cdots y_{j_s}\tilde {v}$
is the desired element since it comes before
$y_{j_1}\cdots y_{j_s}\tilde {v}$
is the desired element since it comes before
![]() $y_{j_1}\cdots y_{j_s}v$
in the ordering of the generators of
$y_{j_1}\cdots y_{j_s}v$
in the ordering of the generators of
![]() $\mathrm {HS}_k(\mathfrak {m} I)$
described before and in addition
$\mathrm {HS}_k(\mathfrak {m} I)$
described before and in addition
![]() $y_{j_1}\cdots y_{j_s}\tilde {v}:y_{j_1}\cdots y_{j_s}v=x_p$
.
$y_{j_1}\cdots y_{j_s}\tilde {v}:y_{j_1}\cdots y_{j_s}v=x_p$
.
Let I, J and L be monomial ideals in S such that the minimal set of monomial generators
![]() $G(I)$
of I is the disjoint union of
$G(I)$
of I is the disjoint union of
![]() $G(J)$
and
$G(J)$
and
![]() $G(L)$
. Then
$G(L)$
. Then
![]() $I=J+L$
is called a Betti splitting if
$I=J+L$
is called a Betti splitting if
for all k and all multidegrees
![]() ${\boldsymbol {a}}$
. In particular, as noted in [Reference Crupi and Ficarra4, Reference Ficarra and Herzog7], if
${\boldsymbol {a}}$
. In particular, as noted in [Reference Crupi and Ficarra4, Reference Ficarra and Herzog7], if
![]() $I=J+L$
is a Betti splitting, then for each k,
$I=J+L$
is a Betti splitting, then for each k,
Theorem 2.5 [Reference Francisco, Há and Van Tuyl8, Corollary 2.4].
Let I, J and L be monomial ideals in S such that
![]() $G(I)$
is the disjoint union of
$G(I)$
is the disjoint union of
![]() $G(J)$
and
$G(J)$
and
![]() $G(L)$
. If both J and L have linear resolutions, then
$G(L)$
. If both J and L have linear resolutions, then
![]() $I=J+L$
is a Betti splitting.
$I=J+L$
is a Betti splitting.
Theorem 2.6. Let G be a graph, and suppose that the graph H is obtained from G by adding a cluster. If the edge ideal
![]() $I(G^c)$
has homological linear quotients, then
$I(G^c)$
has homological linear quotients, then
![]() $I(H^c)$
also has homological linear quotients.
$I(H^c)$
also has homological linear quotients.
Proof. Let
![]() $V(G)=\{x_1,x_2\ldots , x_n\}$
and H be obtained by adding a t-cluster to G via
$V(G)=\{x_1,x_2\ldots , x_n\}$
and H be obtained by adding a t-cluster to G via
![]() $x_n$
. Suppose that
$x_n$
. Suppose that
![]() $y_1,\ldots ,y_t=x_n$
are vertices of the new clique that is added to G. Then
$y_1,\ldots ,y_t=x_n$
are vertices of the new clique that is added to G. Then
Set
![]() $I=I(H^c)$
,
$I=I(H^c)$
,
![]() $J=I(G^c)$
and
$J=I(G^c)$
and
![]() $L=(x_iy_j\mid 1\leq i \leq n-1 \, \mathrm {and}\, 1\leq j \leq t-1 )$
. The ideal L is matroidal. So L has a linear resolution. The ideal J also has a linear resolution by the assumption. Hence, by Theorem 2.5,
$L=(x_iy_j\mid 1\leq i \leq n-1 \, \mathrm {and}\, 1\leq j \leq t-1 )$
. The ideal L is matroidal. So L has a linear resolution. The ideal J also has a linear resolution by the assumption. Hence, by Theorem 2.5,
![]() $I=J+L$
is a Betti splitting. In particular,
$I=J+L$
is a Betti splitting. In particular,
for each k. Observe that
Thus, by Lemma 2.4,
![]() $\mathrm {HS}_{k-1}(J\cap L)$
has linear quotients and
$\mathrm {HS}_{k-1}(J\cap L)$
has linear quotients and
 $$ \begin{align*} \mathrm{HS}_{k-1}(J\cap L)&= (y_1,\ldots,y_{t-1})\mathrm{HS}_{k-1}(J)+(y_iy_j\mid 1\leq i<j\leq t-1)\mathrm{HS}_{k-2}(J)\\ &\quad + (y_iy_jy_k\mid 1\leq i<j<k \leq t-1)\mathrm{HS}_{k-3}(J)+ \cdots\\ &\quad + (y_1\cdots y_{t-1})\mathrm{HS}_{k-t+1}(J). \end{align*} $$
$$ \begin{align*} \mathrm{HS}_{k-1}(J\cap L)&= (y_1,\ldots,y_{t-1})\mathrm{HS}_{k-1}(J)+(y_iy_j\mid 1\leq i<j\leq t-1)\mathrm{HS}_{k-2}(J)\\ &\quad + (y_iy_jy_k\mid 1\leq i<j<k \leq t-1)\mathrm{HS}_{k-3}(J)+ \cdots\\ &\quad + (y_1\cdots y_{t-1})\mathrm{HS}_{k-t+1}(J). \end{align*} $$
Writing the homological shift ideals of
![]() $(x_i \mid 1\leq i \leq n-1 )$
as Koszul complexes and applying Lemma 2.4 yields
$(x_i \mid 1\leq i \leq n-1 )$
as Koszul complexes and applying Lemma 2.4 yields
 $$ \begin{align*} \mathrm{HS}_k(L)=\bigg( x_{i_1}\cdots x_{i_p}y_{j_1}\cdots y_{j_q}\,\bigg|\! \begin{array}{l} 1\leq i_1<\cdots<i_p< n\\ 1\leq j_1<\cdots<j_q< t \end{array} \mathrm{and}\ p+q=k+2\bigg). \end{align*} $$
$$ \begin{align*} \mathrm{HS}_k(L)=\bigg( x_{i_1}\cdots x_{i_p}y_{j_1}\cdots y_{j_q}\,\bigg|\! \begin{array}{l} 1\leq i_1<\cdots<i_p< n\\ 1\leq j_1<\cdots<j_q< t \end{array} \mathrm{and}\ p+q=k+2\bigg). \end{align*} $$
By our discussion, the ideals
![]() $\mathrm {HS}_k(L)$
,
$\mathrm {HS}_k(L)$
,
![]() $\mathrm {HS}_{k-1}(J\cap L)$
and
$\mathrm {HS}_{k-1}(J\cap L)$
and
![]() $\mathrm {HS}_k(J)$
have linear quotients. Suppose that they have linear quotients with respect to the following ordering of their minimal set of monomial generators:
$\mathrm {HS}_k(J)$
have linear quotients. Suppose that they have linear quotients with respect to the following ordering of their minimal set of monomial generators:
-
•
 $\mathrm {HS}_k(L)=(u_1,\ldots ,u_p)$
;
$\mathrm {HS}_k(L)=(u_1,\ldots ,u_p)$
; -
•
 $\mathrm {HS}_{k-1}(J\cap L)=(v_1,\ldots ,v_q)$
;
$\mathrm {HS}_{k-1}(J\cap L)=(v_1,\ldots ,v_q)$
; -
•
 $\mathrm {HS}_k(J)=(w_1,\ldots ,w_r)$
.
$\mathrm {HS}_k(J)=(w_1,\ldots ,w_r)$
.
We claim that
![]() $\mathrm {HS}_k(I)$
has linear quotients with respect to the ordering of generators:
$\mathrm {HS}_k(I)$
has linear quotients with respect to the ordering of generators:
Here
![]() $1\leq j_1<\cdots <j_s\leq q$
and the elements
$1\leq j_1<\cdots <j_s\leq q$
and the elements
![]() $v_{j_1},\ldots ,v_{j_s}$
are those elements of
$v_{j_1},\ldots ,v_{j_s}$
are those elements of
![]() $G(\mathrm {HS}_{k-1}(J\cap L))=\{v_1,\ldots ,v_q\}$
which do not appear among
$G(\mathrm {HS}_{k-1}(J\cap L))=\{v_1,\ldots ,v_q\}$
which do not appear among
![]() $u_1,\ldots ,u_p$
, that is, those elements of
$u_1,\ldots ,u_p$
, that is, those elements of
![]() $G(\mathrm {HS}_{k-1}(J\cap L))$
divided by
$G(\mathrm {HS}_{k-1}(J\cap L))$
divided by
![]() $x_n$
. Let v be a squarefree monomial in
$x_n$
. Let v be a squarefree monomial in
![]() $K[{\boldsymbol {x}},{\boldsymbol {y}}]$
. Denote by
$K[{\boldsymbol {x}},{\boldsymbol {y}}]$
. Denote by ![]() the number of
the number of
![]() $y_j$
which divide v for
$y_j$
which divide v for
![]() $j=1,\ldots ,t$
.
$j=1,\ldots ,t$
.
First consider
![]() $u:v_{j_i}$
for some
$u:v_{j_i}$
for some
![]() $i=1,\ldots ,s$
and
$i=1,\ldots ,s$
and
![]() $u\in \{u_1,\ldots ,u_p,v_1,\ldots ,v_{j_{i-1}}\}$
. Let z be a variable dividing
$u\in \{u_1,\ldots ,u_p,v_1,\ldots ,v_{j_{i-1}}\}$
. Let z be a variable dividing
![]() $u:v_{j_i}$
. Then
$u:v_{j_i}$
. Then
is a monomial appearing among
![]() $u_1,\ldots ,u_p$
in (2.1) and
$u_1,\ldots ,u_p$
in (2.1) and
![]() $\tilde {u}:v_{j_i}=z$
.
$\tilde {u}:v_{j_i}=z$
.
Next consider
![]() $u:w_j$
for some
$u:w_j$
for some
![]() $j=1,\ldots ,r$
and
$j=1,\ldots ,r$
and
![]() $u\in \{u_1,\ldots ,u_p,v_1,\ldots ,v_{j_{s}}\}$
(see (2.1)). Since
$u\in \{u_1,\ldots ,u_p,v_1,\ldots ,v_{j_{s}}\}$
(see (2.1)). Since ![]() , one deduces that
, one deduces that
![]() $y_{j_\ell }$
divides
$y_{j_\ell }$
divides
![]() $u:w_j$
for some
$u:w_j$
for some
![]() $\ell $
. So
$\ell $
. So
![]() $u=(w_j/\max w_j)y_{j_\ell }$
is simply an element of
$u=(w_j/\max w_j)y_{j_\ell }$
is simply an element of
![]() $\{u_1,\ldots ,u_p,v_1,\ldots ,v_{j_{s}}\}$
with
$\{u_1,\ldots ,u_p,v_1,\ldots ,v_{j_{s}}\}$
with
![]() $u:w_j=y_{j_\ell }$
, as desired.
$u:w_j=y_{j_\ell }$
, as desired.
Corollary 2.7. Let G be a block graph. Then the edge ideal
![]() $I(G^c)$
has homological linear quotients.
$I(G^c)$
has homological linear quotients.
Corollary 2.8 [Reference Ficarra and Herzog7, Corollary 3.3].
Let G be a tree. Then the edge ideal
![]() $I(G^c)$
has homological linear quotients.
$I(G^c)$
has homological linear quotients.
3
 $\lambda $
-minimal graphs
$\lambda $
-minimal graphs
Let
![]() $e=\{x_i,x_j\}$
be an edge of a graph G. By adding a pinnacle on e, we mean adding a new vertex y, and edges
$e=\{x_i,x_j\}$
be an edge of a graph G. By adding a pinnacle on e, we mean adding a new vertex y, and edges
![]() $\{x_i,y\}$
and
$\{x_i,y\}$
and
![]() $\{x_j,y\}$
to G. We call the subgraph induced on these two new edges a pinnacle and the vertex y its tip (see Figure 2).
$\{x_j,y\}$
to G. We call the subgraph induced on these two new edges a pinnacle and the vertex y its tip (see Figure 2).
Herzog and Ficarra, using an inductive argument by adding whiskers, showed in [Reference Ficarra and Herzog7] that if G is a tree, then the edge ideal
![]() $I(G^c)$
has homological linear quotients. Here, generalising their result, we determine a labelling on the vertices of trees with some pinnacles to find an admissible ordering of generators for every
$I(G^c)$
has homological linear quotients. Here, generalising their result, we determine a labelling on the vertices of trees with some pinnacles to find an admissible ordering of generators for every
![]() $\mathrm {HS}_k(I(G^c))$
.
$\mathrm {HS}_k(I(G^c))$
.
Theorem 3.1. Let G be either a tree or obtained by adding some pinnacles to a tree. Then the edge ideal
![]() $I(G^c)$
has homological linear quotients.
$I(G^c)$
has homological linear quotients.
Proof. We may assume that
![]() $\{x_1,x_2,\ldots ,x_n\}$
is the vertex set of G such that for some t, the induced subgraph H on
$\{x_1,x_2,\ldots ,x_n\}$
is the vertex set of G such that for some t, the induced subgraph H on
![]() $\{x_t ,x_{t+1},\ldots ,x_n\}$
is a tree and G is obtained by adding some pinnacles to H with tips
$\{x_t ,x_{t+1},\ldots ,x_n\}$
is a tree and G is obtained by adding some pinnacles to H with tips
![]() $\{x_1,x_2,\ldots ,x_{t-1}\}$
. By a suitable relabelling of vertices, we may also assume that if
$\{x_1,x_2,\ldots ,x_{t-1}\}$
. By a suitable relabelling of vertices, we may also assume that if
![]() $t \leq i,j\leq n$
and
$t \leq i,j\leq n$
and ![]() , then
, then
![]() $i<j$
.
$i<j$
.
One can see that the labelling described above gives a perfect elimination ordering on the vertices of G. In fact, if
![]() $x_i$
is the tip of a pinnacle on an edge
$x_i$
is the tip of a pinnacle on an edge
![]() $\{ x_{j_1},x_{j_2}\}\in E(H)$
, then
$\{ x_{j_1},x_{j_2}\}\in E(H)$
, then
is a clique. Otherwise, if
![]() $x_i$
is a vertex of the tree H with
$x_i$
is a vertex of the tree H with
![]() $i<n$
, the set
$i<n$
, the set
has exactly one element. In contrast, assume that distinct elements
![]() $x_{j_1}$
and
$x_{j_1}$
and
![]() $x_{j_2}$
belong to
$x_{j_2}$
belong to
![]() $\{x_j\in \mathrm {N}_G(x_i) \mid j>i\}$
. Then by labelling the vertices as described above, both
$\{x_j\in \mathrm {N}_G(x_i) \mid j>i\}$
. Then by labelling the vertices as described above, both
![]() $d(x_{j_1},x_n)$
and
$d(x_{j_1},x_n)$
and
![]() $d(x_{j_2},x_n)$
are less than or equal to
$d(x_{j_2},x_n)$
are less than or equal to
![]() $d(x_i,x_n)$
. Hence, there exist a path
$d(x_i,x_n)$
. Hence, there exist a path
![]() $P_1$
from
$P_1$
from
![]() $x_{j_1}$
to
$x_{j_1}$
to
![]() $x_n$
and a path
$x_n$
and a path
![]() $P_2$
from
$P_2$
from
![]() $x_{j_2}$
to
$x_{j_2}$
to
![]() $x_n$
neither of which contains
$x_n$
neither of which contains
![]() $x_i$
. This yields the existence of two paths from
$x_i$
. This yields the existence of two paths from
![]() $x_i$
to
$x_i$
to
![]() $x_n$
, one via the adjacent vertex
$x_n$
, one via the adjacent vertex
![]() $x_{j_1}$
and
$x_{j_1}$
and
![]() $P_1$
, and the other via the adjacent vertex
$P_1$
, and the other via the adjacent vertex
![]() $x_{j_2}$
and
$x_{j_2}$
and
![]() $P_2$
, a contradiction to the fact that H is a tree. Thus, the labelling of
$P_2$
, a contradiction to the fact that H is a tree. Thus, the labelling of
![]() $V(G)$
gives a perfect elimination ordering and, by Theorem 2.3, for each k, the kth homological shift ideal of
$V(G)$
gives a perfect elimination ordering and, by Theorem 2.3, for each k, the kth homological shift ideal of
![]() $I=I(G^c)$
is
$I=I(G^c)$
is
Fix k in the set
![]() $\{0,\ldots ,\mathrm {proj\, dim\,} I\}$
. We will show that
$\{0,\ldots ,\mathrm {proj\, dim\,} I\}$
. We will show that
![]() $\mathrm {HS}_k(I)$
has linear quotients with respect to the lexicographic ordering of generators with
$\mathrm {HS}_k(I)$
has linear quotients with respect to the lexicographic ordering of generators with
![]() $x_1>\cdots >x_n$
. For this purpose, suppose that u and v are two monomials in the minimal set of monomial generators of
$x_1>\cdots >x_n$
. For this purpose, suppose that u and v are two monomials in the minimal set of monomial generators of
![]() $\mathrm {HS}_k(I)$
,
$\mathrm {HS}_k(I)$
,
![]() $u>_{\mathrm {lex}} v$
, and
$u>_{\mathrm {lex}} v$
, and
with
![]() $p>1$
and
$p>1$
and
![]() ${i_1}<\cdots <{i_p}$
. Since
${i_1}<\cdots <{i_p}$
. Since
![]() $\mathrm {HS}_k(I)$
is generated in a single degree, the monomial
$\mathrm {HS}_k(I)$
is generated in a single degree, the monomial
![]() $v:u$
is also of degree p, say
$v:u$
is also of degree p, say
Notice that
![]() $u>_{\mathrm {lex}} v$
implies that
$u>_{\mathrm {lex}} v$
implies that
We show that there exists a monomial w in the minimal set of monomial generators of
![]() $\mathrm {HS}_k(I)$
, such that
$\mathrm {HS}_k(I)$
, such that
![]() $w>_{\mathrm {lex}} v$
, and
$w>_{\mathrm {lex}} v$
, and
for some
![]() $s= 1,\ldots ,p$
.
$s= 1,\ldots ,p$
.

Figure 2 A tree on the vertex set
![]() $\{x_1,\ldots,x_4\}$
with three pinnacles.
$\{x_1,\ldots,x_4\}$
with three pinnacles.
First, suppose that
![]() $i_1\geq t$
, so that
$i_1\geq t$
, so that
![]() $x_{i_1}$
is a vertex of the tree H. As discussed above, the vertex
$x_{i_1}$
is a vertex of the tree H. As discussed above, the vertex
![]() $x_{i_1}$
is adjacent to at most one vertex
$x_{i_1}$
is adjacent to at most one vertex
![]() $x_j$
of the tree H with
$x_j$
of the tree H with
![]() $j>i_1$
. From (3.2),
$j>i_1$
. From (3.2),
![]() $x_{i_1}$
is adjacent to at most one of
$x_{i_1}$
is adjacent to at most one of
![]() $x_{\ell _1}$
or
$x_{\ell _1}$
or
![]() $x_{\ell _2}$
; say
$x_{\ell _2}$
; say
Then the variable
![]() $x_{i_1}$
becomes a source of
$x_{i_1}$
becomes a source of
![]() $w=(v/x_{\ell _1})x_{i_1}$
with respect to
$w=(v/x_{\ell _1})x_{i_1}$
with respect to
![]() $G^c$
; here,
$G^c$
; here,
![]() ${i_1<\ell _2}$
guarantees that
${i_1<\ell _2}$
guarantees that
![]() $i_1\neq \max w$
. Furthermore, by (3.2),
$i_1\neq \max w$
. Furthermore, by (3.2),
![]() $w>_{\mathrm {lex}}v$
. Thus, w is a monomial with the desired properties.
$w>_{\mathrm {lex}}v$
. Thus, w is a monomial with the desired properties.
Next, suppose that
![]() $i_1< t$
, so that
$i_1< t$
, so that
![]() $x_{i_1}$
is the tip of a pinnacle. From the labelling given to the vertices of G,
$x_{i_1}$
is the tip of a pinnacle. From the labelling given to the vertices of G,
for vertices
![]() $x_{t_1}$
and
$x_{t_1}$
and
![]() $x_{t_2}$
on an edge of the tree H which is on a pinnacle with the tip
$x_{t_2}$
on an edge of the tree H which is on a pinnacle with the tip
![]() $x_{i_1}$
. We consider three cases.
$x_{i_1}$
. We consider three cases.
Case 1. If neither of the vertices
![]() $x_{t_1}$
and
$x_{t_1}$
and
![]() $x_{t_2}$
divides v, then
$x_{t_2}$
divides v, then
![]() $x_{i_1}$
is a source of the monomial
$x_{i_1}$
is a source of the monomial
![]() $w=(v/x_{\ell _1})x_{i_1}$
with respect to
$w=(v/x_{\ell _1})x_{i_1}$
with respect to
![]() $G^c$
. By (3.2),
$G^c$
. By (3.2),
![]() $i_1<\ell _2\leq \max w$
. Hence, the squarefree monomial
$i_1<\ell _2\leq \max w$
. Hence, the squarefree monomial
![]() $w=(v/x_{\ell _1})x_{i_1}$
of degree
$w=(v/x_{\ell _1})x_{i_1}$
of degree
![]() $k+2$
is an element of
$k+2$
is an element of
![]() $\mathrm {HS}_k(I)$
by (3.1). Furthermore,
$\mathrm {HS}_k(I)$
by (3.1). Furthermore,
![]() $w:v=x_{i_1}$
and, by (3.2),
$w:v=x_{i_1}$
and, by (3.2),
![]() $w>_{\mathrm {lex}} v$
, as desired.
$w>_{\mathrm {lex}} v$
, as desired.
Case 2. Assume that exactly one of the variables
![]() $x_{t_1}$
and
$x_{t_1}$
and
![]() $x_{t_2}$
divides v, say
$x_{t_2}$
divides v, say
![]() $x_{t_1}$
. Then by (3.3), the variable
$x_{t_1}$
. Then by (3.3), the variable
![]() $x_{i_1}$
is a source of the monomial
$x_{i_1}$
is a source of the monomial
![]() $w=(v/x_{t_1})x_{i_1}$
with respect to
$w=(v/x_{t_1})x_{i_1}$
with respect to
![]() $G^c$
. Here,
$G^c$
. Here,
![]() $i_1<\max w$
is a consequence of
$i_1<\max w$
is a consequence of
![]() $i_1<\ell _1<\ell _2\leq \max v$
by (3.2). Now since
$i_1<\ell _1<\ell _2\leq \max v$
by (3.2). Now since
![]() $w=(v/x_{t_1})x_{i_1}$
has a source with respect to
$w=(v/x_{t_1})x_{i_1}$
has a source with respect to
![]() $G^c$
, this squarefree monomial of degree
$G^c$
, this squarefree monomial of degree
![]() $k+2$
is an element of
$k+2$
is an element of
![]() $\mathrm {HS}_k(I)$
. Moreover, from the labelling of vertices,
$\mathrm {HS}_k(I)$
. Moreover, from the labelling of vertices,
![]() $i_1<t_1$
because
$i_1<t_1$
because
![]() $i_1$
is a tip, while
$i_1$
is a tip, while
![]() $t_1$
is a vertex of the tree H. So
$t_1$
is a vertex of the tree H. So
![]() $w>_{\mathrm {lex}} v$
and w is a desired monomial.
$w>_{\mathrm {lex}} v$
and w is a desired monomial.
Case 3. Finally, assume that
![]() $x_{t_1}$
and
$x_{t_1}$
and
![]() $x_{t_2}$
both divide v. Suppose that
$x_{t_2}$
both divide v. Suppose that
![]() $t_1<t_2$
. Since v belongs to the minimal set of monomial generators of
$t_1<t_2$
. Since v belongs to the minimal set of monomial generators of
![]() $\mathrm {HS}_k(I)$
, by (3.1), it has a source variable with respect to
$\mathrm {HS}_k(I)$
, by (3.1), it has a source variable with respect to
![]() $G^c$
. Suppose that
$G^c$
. Suppose that
![]() $x_{\ell }$
is a source of v for some
$x_{\ell }$
is a source of v for some
![]() $\ell $
. Since
$\ell $
. Since
![]() $\{x_{t_1},x_{t_2}\}$
is an edge of H and we have assumed that
$\{x_{t_1},x_{t_2}\}$
is an edge of H and we have assumed that
![]() $t_1<t_2$
, it follows that
$t_1<t_2$
, it follows that
![]() $x_{t_1}$
is not a source of v with respect to
$x_{t_1}$
is not a source of v with respect to
![]() $G^c$
. In particular,
$G^c$
. In particular,
![]() $x_{t_1}\neq x_{\ell }$
. We show that if either
$x_{t_1}\neq x_{\ell }$
. We show that if either
![]() $t_1<\ell $
or
$t_1<\ell $
or
![]() $\ell <t_1$
, the variable
$\ell <t_1$
, the variable
![]() $x_{\ell }$
remains a source in
$x_{\ell }$
remains a source in
![]() $w=(v/x_{t_1})x_{i_1}$
. When
$w=(v/x_{t_1})x_{i_1}$
. When
![]() $t_1<\ell $
, it is clear that
$t_1<\ell $
, it is clear that
![]() $x_{\ell }$
is still a source of
$x_{\ell }$
is still a source of
![]() $w=(v/x_{t_1})x_{i_1}$
because the replacement of
$w=(v/x_{t_1})x_{i_1}$
because the replacement of
![]() $x_{i_1}$
by
$x_{i_1}$
by
![]() $x_{t_1}$
in w occurs before
$x_{t_1}$
in w occurs before
![]() $x_\ell $
. However, if
$x_\ell $
. However, if
![]() $\ell <t_1$
, then
$\ell <t_1$
, then
![]() $\ell $
is not adjacent to
$\ell $
is not adjacent to
![]() $i_1$
because
$i_1$
because
![]() $i_1$
is a tip in G with
$i_1$
is a tip in G with
![]() $N_G(x_{i_1})=\{x_{t_1},x_{t_2}\}$
. So the set
$N_G(x_{i_1})=\{x_{t_1},x_{t_2}\}$
. So the set
is still the empty set. Moreover,
![]() $x_{\ell }\neq \max w$
because
$x_{\ell }\neq \max w$
because
![]() $x_{t_2}$
divides w. Thus,
$x_{t_2}$
divides w. Thus,
![]() $x_\ell $
is a source of w as well. Again, note that we have set the tip
$x_\ell $
is a source of w as well. Again, note that we have set the tip
![]() $x_{i_1}$
lexicographically greater than the vertex
$x_{i_1}$
lexicographically greater than the vertex
![]() $x_{t_1}$
of H. Hence,
$x_{t_1}$
of H. Hence,
![]() $w>_{\mathrm {lex}}v$
, as desired.
$w>_{\mathrm {lex}}v$
, as desired.
Proposition 3.2. Let G be either the complete graph
![]() $K_3$
or obtained by adding some pinnacles to
$K_3$
or obtained by adding some pinnacles to
![]() $K_3$
. Then the edge ideal
$K_3$
. Then the edge ideal
![]() $I(G^c)$
has homological linear quotients.
$I(G^c)$
has homological linear quotients.
Proof. Set
![]() $I=I(G^c)$
. Assume that
$I=I(G^c)$
. Assume that
![]() $V(G)=\{x_1,\ldots ,x_n\}$
for some
$V(G)=\{x_1,\ldots ,x_n\}$
for some
![]() $n\geq 3$
, the subgraph H induced on
$n\geq 3$
, the subgraph H induced on
![]() $\{x_{n-2},x_{n-1},x_n\}$
is a 3-clique, and G is constructed by adding pinnacles with tips
$\{x_{n-2},x_{n-1},x_n\}$
is a 3-clique, and G is constructed by adding pinnacles with tips
![]() $\{x_1,\ldots ,x_{n-3}\}$
. Fixing
$\{x_1,\ldots ,x_{n-3}\}$
. Fixing
![]() $0\leq k\leq \mathrm {proj\, dim\,} I(G^c)$
, we are going to show that
$0\leq k\leq \mathrm {proj\, dim\,} I(G^c)$
, we are going to show that
![]() $\mathrm {HS}_k(I(G^c))$
has linear quotients with respect to the lexicographic ordering of its minimal set of monomial generators induced by
$\mathrm {HS}_k(I(G^c))$
has linear quotients with respect to the lexicographic ordering of its minimal set of monomial generators induced by
![]() $x_1>\cdots >x_n$
. For this purpose, first we see that if w is an element of the minimal set of monomial generators of
$x_1>\cdots >x_n$
. For this purpose, first we see that if w is an element of the minimal set of monomial generators of
![]() $\mathrm {HS}_k(I)$
, then at most one of the vertices
$\mathrm {HS}_k(I)$
, then at most one of the vertices
![]() $x_{n-2}$
,
$x_{n-2}$
,
![]() $x_{n-1}$
,
$x_{n-1}$
,
![]() $x_{n}$
can divide w. Indeed, the neighbourhood of each vertex of G intersects
$x_{n}$
can divide w. Indeed, the neighbourhood of each vertex of G intersects
![]() $\{x_{n-2},x_{n-1},x_n\}$
exactly in two vertices, and if more than one variable among
$\{x_{n-2},x_{n-1},x_n\}$
exactly in two vertices, and if more than one variable among
![]() $x_{n-2}$
,
$x_{n-2}$
,
![]() $x_{n-1}$
or
$x_{n-1}$
or
![]() $x_{n}$
divides w, then w does not have a source with respect to
$x_{n}$
divides w, then w does not have a source with respect to
![]() $G^c$
, which is a contradiction. (See Theorem 2.3 where the generators of
$G^c$
, which is a contradiction. (See Theorem 2.3 where the generators of
![]() $\mathrm {HS}_k(I)$
are described.)
$\mathrm {HS}_k(I)$
are described.)
Next, let u and v be two monomials in the minimal set of monomial generators of
![]() $\mathrm {HS}_k(I)$
,
$\mathrm {HS}_k(I)$
,
![]() $u>_{\mathrm {lex}} v$
, and
$u>_{\mathrm {lex}} v$
, and
![]() $ u:v= x_{i_1}\cdots x_{i_p} $
with
$ u:v= x_{i_1}\cdots x_{i_p} $
with
![]() $p>1$
and
$p>1$
and
![]() ${i_1}<\cdots <{i_p}$
. Since
${i_1}<\cdots <{i_p}$
. Since
![]() $\mathrm {HS}_k(I)$
is generated in a single degree, we may write
$\mathrm {HS}_k(I)$
is generated in a single degree, we may write
Now on the one hand,
![]() $u>_{\mathrm {lex}} v$
implies that
$u>_{\mathrm {lex}} v$
implies that
![]() $i_1<\ell _1<\ell _2$
. On the other hand, since at most one of the variables
$i_1<\ell _1<\ell _2$
. On the other hand, since at most one of the variables
![]() $x_{n-2}$
,
$x_{n-2}$
,
![]() $x_{n-1}$
or
$x_{n-1}$
or
![]() $x_{n}$
divides v, we deduce that
$x_{n}$
divides v, we deduce that
![]() $\ell _1\leq n-3$
. Hence,
$\ell _1\leq n-3$
. Hence,
![]() $i_1<n-3$
. In particular, the vertices
$i_1<n-3$
. In particular, the vertices
![]() $x_{\ell _1}$
and
$x_{\ell _1}$
and
![]() $x_{i_1}$
are the tips of two pinnacles in G. Consequently, if
$x_{i_1}$
are the tips of two pinnacles in G. Consequently, if
![]() $m=\max v$
, then
$m=\max v$
, then
![]() $x_{i_1}$
is a source of
$x_{i_1}$
is a source of
![]() $w=(v/x_m)x_{i_1}$
. To see this, note that
$w=(v/x_m)x_{i_1}$
. To see this, note that
![]() $i_1<\ell _1<\ell _2\leq \max v$
and, by removing
$i_1<\ell _1<\ell _2\leq \max v$
and, by removing
![]() $x_m$
from v, the monomial w can have only variables corresponding to some tips in its support. So
$x_m$
from v, the monomial w can have only variables corresponding to some tips in its support. So
![]() $x_{i_1}$
is not adjacent to any of the
$x_{i_1}$
is not adjacent to any of the
![]() $x_j$
in the support of
$x_j$
in the support of
![]() $v/x_m$
. So w is a monomial in
$v/x_m$
. So w is a monomial in
![]() $\mathrm {HS}_k(I)$
, as described in Theorem 2.3, with
$\mathrm {HS}_k(I)$
, as described in Theorem 2.3, with
![]() $w>_{\mathrm {lex}} v$
and
$w>_{\mathrm {lex}} v$
and
![]() $w:v=x_{i_1}$
.
$w:v=x_{i_1}$
.
The statement of Proposition 3.2 does not hold if we replace
![]() $K_3$
by an arbitrary complete graph. For example, consider the graph G in Figure 1 obtained by adding two pinnacles to
$K_3$
by an arbitrary complete graph. For example, consider the graph G in Figure 1 obtained by adding two pinnacles to
![]() $K_4$
, and refer to Remark 2.2 where
$K_4$
, and refer to Remark 2.2 where
![]() $\mathrm {HS}_2(I(G^c))$
is determined.
$\mathrm {HS}_2(I(G^c))$
is determined.
Let G be a graph and k be a positive integer. A k-colouring of G is a mapping from
![]() $V(G)$
to
$V(G)$
to
![]() $[k]$
. If f is a k-colouring of G, then the colour of each edge
$[k]$
. If f is a k-colouring of G, then the colour of each edge
![]() $\{x_i,x_j\}$
is defined to be
$\{x_i,x_j\}$
is defined to be
![]() $\{f(x_i),f(x_j)\}$
. A k-colouring f of the graph G is called a line-distinguishing colouring if every two distinct edges of G have distinct colours. The minimum number k for which G has a line-distinguishing k-colouring, denoted by
$\{f(x_i),f(x_j)\}$
. A k-colouring f of the graph G is called a line-distinguishing colouring if every two distinct edges of G have distinct colours. The minimum number k for which G has a line-distinguishing k-colouring, denoted by
![]() $\lambda (G)$
, is called the line-distinguishing chromatic number of G. The graph G is called
$\lambda (G)$
, is called the line-distinguishing chromatic number of G. The graph G is called
![]() $\lambda $
-minimal in [Reference Frank, Harary and Plantholt9] if
$\lambda $
-minimal in [Reference Frank, Harary and Plantholt9] if
![]() $\lambda (G-e)=\lambda (G)-1$
for each edge e.
$\lambda (G-e)=\lambda (G)-1$
for each edge e.
Theorem 3.3 [Reference Regonati and Salvi16, Theorem 2.4].
Let G be a chordal graph. Then G is
![]() $\lambda $
-minimal if and only if G is either constructed by adding at least one pinnacle to each edge of a star or constructed by adding at least one pinnacle to each edge of the complete graph
$\lambda $
-minimal if and only if G is either constructed by adding at least one pinnacle to each edge of a star or constructed by adding at least one pinnacle to each edge of the complete graph
![]() $K_3$
.
$K_3$
.
Corollary 3.4. Let G be a
![]() $\lambda $
-minimal chordal graph. Then the edge ideal
$\lambda $
-minimal chordal graph. Then the edge ideal
![]() $I(G^c)$
has homological linear quotients.
$I(G^c)$
has homological linear quotients.